2021-2022学年人教版数学九年级下册26.1.2反比例函数的图像和性质提升练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册26.1.2反比例函数的图像和性质提升练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 517.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 14:37:43 | ||
图片预览



文档简介
反比例函数的图像和性质 提升练习
一、单选题
1.将点P(3,4)向下平移1个单位长度后,落在函数的图象上,则k的值为( )
A. B. C. D.
2.若函数的图象是双曲线,则的值为( )
A. B. C. D.
3.反比例函数y=的图象,当x<0时,y随x的增大而增大,则k的取值范围为( )
A.k≥2 B.k≤﹣2 C.k>2 D.k<﹣2
4.若点都在反比例函数的图象上,且.则、、的大小关系是( )
A. B. C. D.
5.已知反比例函数,则下列描述不正确的是( )
A.图象位于第二、第四象限 B.图象必经过点
C.图象不可能与坐标轴相交 D.y随x的增大而增大
6.下列关系式能表示y关于x的反比例函数的是( )
A. B. C. D.
7.若点A(﹣3,2)关于x轴的对称点A′恰好在反比例函数y=(k≠0)的图象上,则k的值为( )
A.﹣5 B.﹣1 C.6 D.﹣6
8.反比例函数的图象如图所示,则下列结论正确的是( )
A.常数
B.随的增大而增大
C.若,在该图象上,则
D.若在该图象上,则也在该图象上
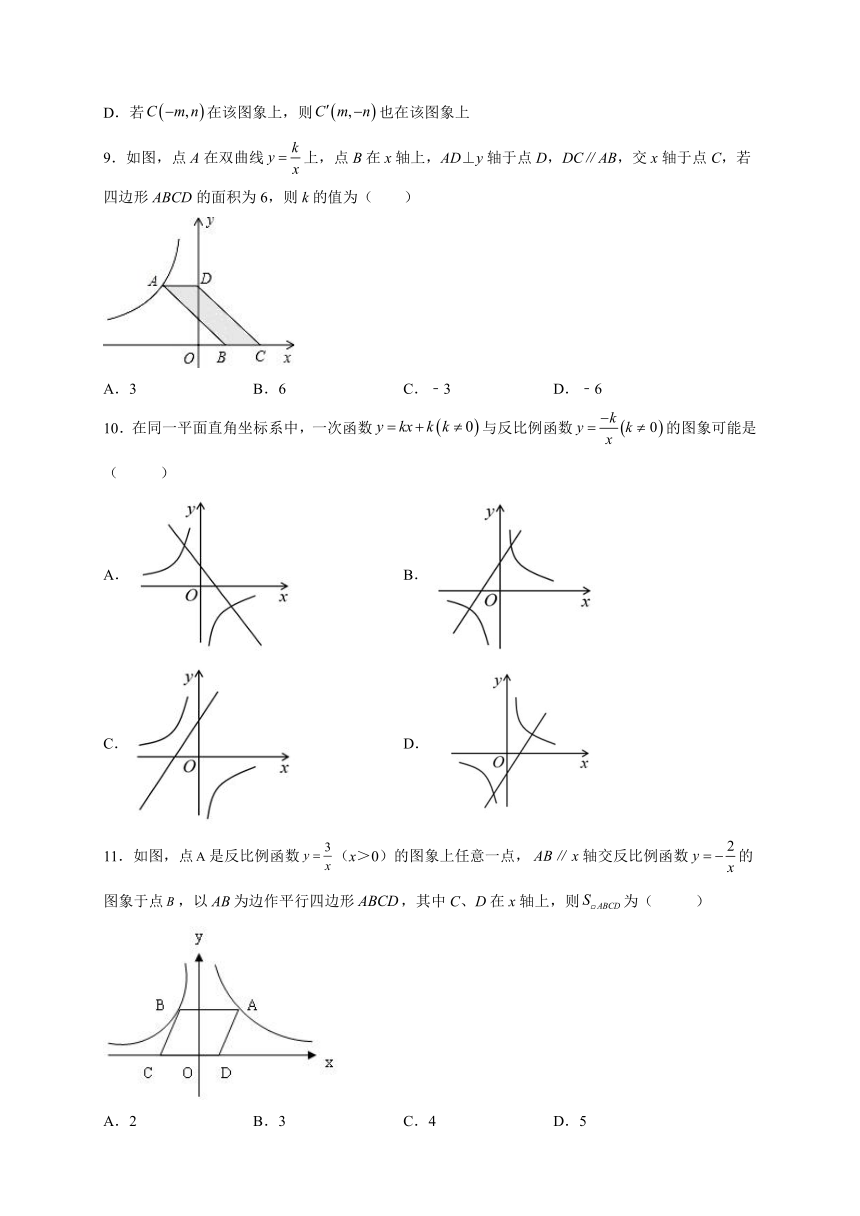
9.如图,点A在双曲线上,点B在x轴上,AD⊥y轴于点D,DC∥AB,交x轴于点C,若四边形ABCD的面积为6,则k的值为( )
A.3 B.6 C.﹣3 D.﹣6
10.在同一平面直角坐标系中,一次函数与反比例函数的图象可能是( )
A. B.
C. D.
11.如图,点是反比例函数(x>0)的图象上任意一点,轴交反比例函数的图象于点,以为边作平行四边形,其中C、D在x轴上,则为( )
A.2 B.3 C.4 D.5
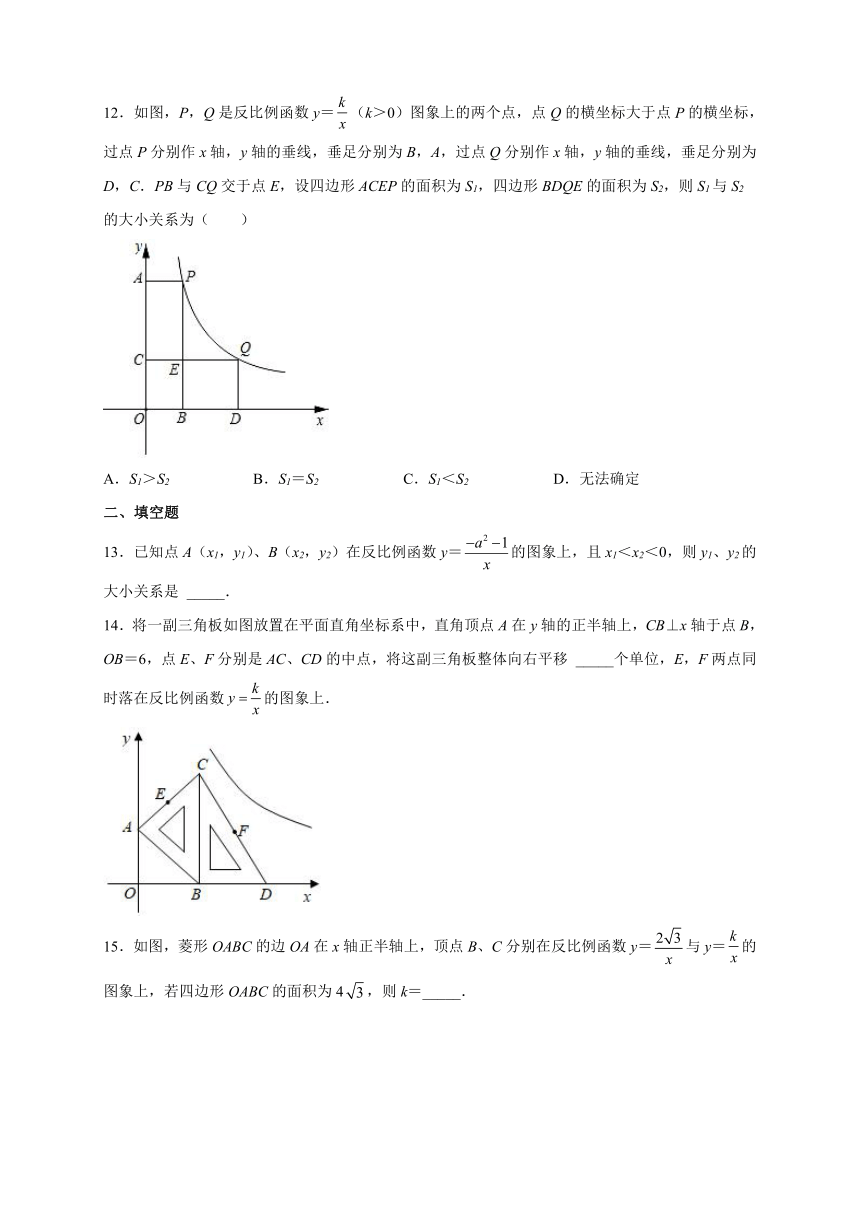
12.如图,P,Q是反比例函数y=(k>0)图象上的两个点,点Q的横坐标大于点P的横坐标,过点P分别作x轴,y轴的垂线,垂足分别为B,A,过点Q分别作x轴,y轴的垂线,垂足分别为D,C.PB与CQ交于点E,设四边形ACEP的面积为S1,四边形BDQE的面积为S2,则S1与S2的大小关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
二、填空题
13.已知点A(x1,y1)、B(x2,y2)在反比例函数y=的图象上,且x1<x2<0,则y1、y2的大小关系是 _____.
14.将一副三角板如图放置在平面直角坐标系中,直角顶点A在y轴的正半轴上,CB⊥x轴于点B,OB=6,点E、F分别是AC、CD的中点,将这副三角板整体向右平移 _____个单位,E,F两点同时落在反比例函数的图象上.
15.如图,菱形OABC的边OA在x轴正半轴上,顶点B、C分别在反比例函数y=与y=的图象上,若四边形OABC的面积为4,则k=_____.
16.如图,在平面直角坐标系中,Rt△ABC的顶点A,C的坐标分别是(0,2),(2,0),∠ACB=90°,AC=2BC.若函数y(k>0,x>0)的图象经过点B,则k的值为______.
三、解答题
17.1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径米是其两腿迈出的步长之差厘米的反比例函数,其图象如图所示.
请根据图象中的信息解决下列问题:
(1)求与之间的函数表达式;
(2)当某人两腿迈出的步长之差为厘米时,他蒙上眼睛走出的大圆圈的半径为______米;
(3)若某人蒙上眼睛走出的大圆圈的半径不小于米,则其两腿迈出的步长之差最多是多少厘米
18.如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.求反比例函数的解析式.
19.如图,点A(1,m),B(6,n)在反比例函数图象上,AD⊥y轴于点D,BC⊥y轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连结AB,在线段DC上是否存在一点P,使△PAB的面积等于10?若存在,求出P点坐标;若不存在,请说明理由.
20.如图,一次函数y1=﹣x+2的图象与反比例函数y=的图象交于点A(﹣1,m),点B(n,﹣1).
(1)求反比例函数的解析式;
(2)当y1>y时,直接写出x的取值范围;
(3)求△AOB的面积.
21.如图,一次函数的图象与反比例函数的图象相交于A、B两点,其中点A的坐标为,点B的坐标为.
(1)求这两个函数的表达式:
(2)根据图象,直接写出满足的x的取值范围;
(3)连接OA,OB,求的面积;
(4)点P在线段AB上,且,求点P的坐标.
试卷第1页,共3页
参考答案:
1.C
解:点P(3,4)向下平移1个单位长度后得到点(3,3),
把(3,3)代入函数中,得k=9,
故选C.
2.D
解:函数的图象是双曲线,
∴该函数为反比例函数,
∴且,
解得:.
故选: D
3.C
解:∵反比例函数,当x<0时y随x的增大而增大,
∴2﹣k<0,
解得k>2.
故选C.
4.D
解:反比例函数中k= 3<0
∴函数图像的两支分别位于二、四象限,且在每个象限内,y随x的增大而增大,
∵
∴A(x1,y1),B(x2,y2)两点在第四象限,C(x3,y3)点在第二象限,
∴
故选:D.
5.D
解:A.∵k=,
∴图象位于第二、第四象限,
故A正确,不符合题意;
B.∵=k,
∴图象必经过点,
故B正确,不符合题意;
C.∵x≠0,
∴y≠0,
∴图象不可能与坐标轴相交,
故C正确,不符合题意;
D.∵k=,
∴在每一个象限内,y随x的增大而增大,
故D错误,符合题意.
故选:D.
6.B
解:反比例函数的表达式形如
A中不满足函数的定义,对于自变量x都有唯一一个确定的y与之对应,错误,不符合题意;
B项正确,符合题意;
C中为一次函数,错误,不符合题意;
D中为二次函数,错误,不符合题意;
故选B.
7.C
解:∵点A′与点A(-3,2)关于x轴的对称,
∴点A′(-3,-2),
又∵点A′(-3,-2)在反比例函数y=(k≠0)的图象上,
∴k=(-3)×(-2)=6,
故选:C.
8.D
解:A. 反比例函数图象在二、四象限,所以常数,不符合题意;
B. 在每个象限内,反比例函数随的增大而增大,不符合题意;
C. 若,在该图象上,则,不符合题意;
D. 因为,,所以若在该图象上,则也在该图象上,符合题意;
故选:D.
9.D
解:如图,过点A作AE⊥EC于点E.
∵AD⊥y轴于点D,
∴AD∥BC.
又∵DC∥AB,
∴四边形ADCB是平行四边形,
∴矩形ADOE的面积=平行四边形ADCB的面积=6,即|k|=6.
又∵双曲线经过第二、四象限,
∴k<0,
∴k=﹣6.
故选:D.
10.C
解:当时,的图象过一二三象限,的图象过二四象限;
∴与C选项中图象一致
故选C.
11.D
解:设A的纵坐标是b,
∵轴,
∴点B的纵坐标也是b.
把y=b代入得,,则,即A的横坐标是,
把y=b代入得,,则,即B的横坐标是,
则,
则.
故选:D.
12.B
解:∵P,Q是反比例函数y=(k>0)图象上的两个点,
∴OA OB=OC OD=k,
∴S四边形AOBP=S四边形ODQC,
∴S四边形AOBP﹣S四边形OBEC=S四边形ODQC﹣S四边形OBEC,
∴S1=S2.
故选:B.
13.##
解:∵,,
∴,
∴该反比例函数图像在二、四象限,在第一象限内随着的增大而增大,
∵,
∴.
故答案为:.
14.
解:∵OB=6,
∴OA=6,AB=OB=6,
∴BC=AB=×=12,
∴A(0,6),C(6,12),
∵点E是AC的中点,
∴E的坐标为(3,9),
∵BC=12,∠BDC=60°,
∴BD=BC=4,
∴OD=6+4,
∴D(6+4,0),
∵F是CD的中点,
∴F(6+2,6),
设平移t个单位后,则平移后F点的坐标为(6+2+t,6),平移后E点的坐标为(3+t,9),
∵平移后E,F两点同时落在反比例函数y=的图象上,
∴(6+2+t)×6=(3+t)×9,
解得t=3+4,
故答案为.
15.
解:如图,连接,设直线与轴交于点,
四边形是菱形,且面积为,
,
轴,
轴,
,分别在反比例函数与的图象上,
,,
解得,(正值舍去).
故答案为:.
16.3
解:如图,过作于
A,C的坐标分别是(0,2),(2,0),
故答案为:3
17.(1);(2);(3)步数之差最多是厘米,
解:(1)设反比例函数解析式为,
将,代入解析式得:,
解得:,
反比例函数解析式为;
(2)将代入得;
(3)反比例函数,
在每一象限随增大而减小,
当时,,
解得:,
当时,,
步数之差最多是厘米.
18.反比例函数的解析式为y=-.
解:∵将坐标原点O沿x轴向左平移2个单位长度得到点A,
∴OA=2,
∵AB//y轴,AB=,
∴B点坐标为:(-2,),
把B(-2,),代入y=中,得到k=-3,
∴反比例函数的解析式为y=-.
19.(1)
(2)存在,
解:(1)
点A(1,m),B(6,n)在反比例函数图象上,DC=5.
依题意,
解得
设反比例函数的解析式为,则
反比例函数的解析式为
(2)
存在,,理由如下,
如图,连接,设
,
,
,
解得
20.(1);(2)x<-1或0<x<3; (3)4.
解:(1)A(﹣1,m)代入y1=﹣x+2得m=1+2=3,∴A(-1,3),
将A点坐标(-1,3)代入,得,解得,k=-3
∴反比例函数的解析式为;
(2)易得,n=3,∴B(3,-1)
x<-1或0<x<3;
(3)如图,作AD成长x轴于点D,BE⊥x轴于点E,
则AD=3,BD=1,
易得,AB与x轴交点C(2,0),OC=2,
∴S△ABC=S△AOC+S△BOC=.
21.(1),;
(2)或;
(3);
(4)
(1)
解:把代入,得,
∴,
∵点在上,
∴,
∴,
把,代入得
,解得,
∴;
(2)
解:观察图象可知当或 ;
(3)
解:如图,
设与轴交于点,
∵点在直线上,
∴,
∴;
(4)
解:如图,
∵S△AOP:S△BOP=1:2,
∴,,
又,
∴点在第一象限,
∴,
又,
∴,解得,
把代入,得,
∴.
答案第1页,共2页
一、单选题
1.将点P(3,4)向下平移1个单位长度后,落在函数的图象上,则k的值为( )
A. B. C. D.
2.若函数的图象是双曲线,则的值为( )
A. B. C. D.
3.反比例函数y=的图象,当x<0时,y随x的增大而增大,则k的取值范围为( )
A.k≥2 B.k≤﹣2 C.k>2 D.k<﹣2
4.若点都在反比例函数的图象上,且.则、、的大小关系是( )
A. B. C. D.
5.已知反比例函数,则下列描述不正确的是( )
A.图象位于第二、第四象限 B.图象必经过点
C.图象不可能与坐标轴相交 D.y随x的增大而增大
6.下列关系式能表示y关于x的反比例函数的是( )
A. B. C. D.
7.若点A(﹣3,2)关于x轴的对称点A′恰好在反比例函数y=(k≠0)的图象上,则k的值为( )
A.﹣5 B.﹣1 C.6 D.﹣6
8.反比例函数的图象如图所示,则下列结论正确的是( )
A.常数
B.随的增大而增大
C.若,在该图象上,则
D.若在该图象上,则也在该图象上
9.如图,点A在双曲线上,点B在x轴上,AD⊥y轴于点D,DC∥AB,交x轴于点C,若四边形ABCD的面积为6,则k的值为( )
A.3 B.6 C.﹣3 D.﹣6
10.在同一平面直角坐标系中,一次函数与反比例函数的图象可能是( )
A. B.
C. D.
11.如图,点是反比例函数(x>0)的图象上任意一点,轴交反比例函数的图象于点,以为边作平行四边形,其中C、D在x轴上,则为( )
A.2 B.3 C.4 D.5
12.如图,P,Q是反比例函数y=(k>0)图象上的两个点,点Q的横坐标大于点P的横坐标,过点P分别作x轴,y轴的垂线,垂足分别为B,A,过点Q分别作x轴,y轴的垂线,垂足分别为D,C.PB与CQ交于点E,设四边形ACEP的面积为S1,四边形BDQE的面积为S2,则S1与S2的大小关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
二、填空题
13.已知点A(x1,y1)、B(x2,y2)在反比例函数y=的图象上,且x1<x2<0,则y1、y2的大小关系是 _____.
14.将一副三角板如图放置在平面直角坐标系中,直角顶点A在y轴的正半轴上,CB⊥x轴于点B,OB=6,点E、F分别是AC、CD的中点,将这副三角板整体向右平移 _____个单位,E,F两点同时落在反比例函数的图象上.
15.如图,菱形OABC的边OA在x轴正半轴上,顶点B、C分别在反比例函数y=与y=的图象上,若四边形OABC的面积为4,则k=_____.
16.如图,在平面直角坐标系中,Rt△ABC的顶点A,C的坐标分别是(0,2),(2,0),∠ACB=90°,AC=2BC.若函数y(k>0,x>0)的图象经过点B,则k的值为______.
三、解答题
17.1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径米是其两腿迈出的步长之差厘米的反比例函数,其图象如图所示.
请根据图象中的信息解决下列问题:
(1)求与之间的函数表达式;
(2)当某人两腿迈出的步长之差为厘米时,他蒙上眼睛走出的大圆圈的半径为______米;
(3)若某人蒙上眼睛走出的大圆圈的半径不小于米,则其两腿迈出的步长之差最多是多少厘米
18.如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.求反比例函数的解析式.
19.如图,点A(1,m),B(6,n)在反比例函数图象上,AD⊥y轴于点D,BC⊥y轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连结AB,在线段DC上是否存在一点P,使△PAB的面积等于10?若存在,求出P点坐标;若不存在,请说明理由.
20.如图,一次函数y1=﹣x+2的图象与反比例函数y=的图象交于点A(﹣1,m),点B(n,﹣1).
(1)求反比例函数的解析式;
(2)当y1>y时,直接写出x的取值范围;
(3)求△AOB的面积.
21.如图,一次函数的图象与反比例函数的图象相交于A、B两点,其中点A的坐标为,点B的坐标为.
(1)求这两个函数的表达式:
(2)根据图象,直接写出满足的x的取值范围;
(3)连接OA,OB,求的面积;
(4)点P在线段AB上,且,求点P的坐标.
试卷第1页,共3页
参考答案:
1.C
解:点P(3,4)向下平移1个单位长度后得到点(3,3),
把(3,3)代入函数中,得k=9,
故选C.
2.D
解:函数的图象是双曲线,
∴该函数为反比例函数,
∴且,
解得:.
故选: D
3.C
解:∵反比例函数,当x<0时y随x的增大而增大,
∴2﹣k<0,
解得k>2.
故选C.
4.D
解:反比例函数中k= 3<0
∴函数图像的两支分别位于二、四象限,且在每个象限内,y随x的增大而增大,
∵
∴A(x1,y1),B(x2,y2)两点在第四象限,C(x3,y3)点在第二象限,
∴
故选:D.
5.D
解:A.∵k=,
∴图象位于第二、第四象限,
故A正确,不符合题意;
B.∵=k,
∴图象必经过点,
故B正确,不符合题意;
C.∵x≠0,
∴y≠0,
∴图象不可能与坐标轴相交,
故C正确,不符合题意;
D.∵k=,
∴在每一个象限内,y随x的增大而增大,
故D错误,符合题意.
故选:D.
6.B
解:反比例函数的表达式形如
A中不满足函数的定义,对于自变量x都有唯一一个确定的y与之对应,错误,不符合题意;
B项正确,符合题意;
C中为一次函数,错误,不符合题意;
D中为二次函数,错误,不符合题意;
故选B.
7.C
解:∵点A′与点A(-3,2)关于x轴的对称,
∴点A′(-3,-2),
又∵点A′(-3,-2)在反比例函数y=(k≠0)的图象上,
∴k=(-3)×(-2)=6,
故选:C.
8.D
解:A. 反比例函数图象在二、四象限,所以常数,不符合题意;
B. 在每个象限内,反比例函数随的增大而增大,不符合题意;
C. 若,在该图象上,则,不符合题意;
D. 因为,,所以若在该图象上,则也在该图象上,符合题意;
故选:D.
9.D
解:如图,过点A作AE⊥EC于点E.
∵AD⊥y轴于点D,
∴AD∥BC.
又∵DC∥AB,
∴四边形ADCB是平行四边形,
∴矩形ADOE的面积=平行四边形ADCB的面积=6,即|k|=6.
又∵双曲线经过第二、四象限,
∴k<0,
∴k=﹣6.
故选:D.
10.C
解:当时,的图象过一二三象限,的图象过二四象限;
∴与C选项中图象一致
故选C.
11.D
解:设A的纵坐标是b,
∵轴,
∴点B的纵坐标也是b.
把y=b代入得,,则,即A的横坐标是,
把y=b代入得,,则,即B的横坐标是,
则,
则.
故选:D.
12.B
解:∵P,Q是反比例函数y=(k>0)图象上的两个点,
∴OA OB=OC OD=k,
∴S四边形AOBP=S四边形ODQC,
∴S四边形AOBP﹣S四边形OBEC=S四边形ODQC﹣S四边形OBEC,
∴S1=S2.
故选:B.
13.##
解:∵,,
∴,
∴该反比例函数图像在二、四象限,在第一象限内随着的增大而增大,
∵,
∴.
故答案为:.
14.
解:∵OB=6,
∴OA=6,AB=OB=6,
∴BC=AB=×=12,
∴A(0,6),C(6,12),
∵点E是AC的中点,
∴E的坐标为(3,9),
∵BC=12,∠BDC=60°,
∴BD=BC=4,
∴OD=6+4,
∴D(6+4,0),
∵F是CD的中点,
∴F(6+2,6),
设平移t个单位后,则平移后F点的坐标为(6+2+t,6),平移后E点的坐标为(3+t,9),
∵平移后E,F两点同时落在反比例函数y=的图象上,
∴(6+2+t)×6=(3+t)×9,
解得t=3+4,
故答案为.
15.
解:如图,连接,设直线与轴交于点,
四边形是菱形,且面积为,
,
轴,
轴,
,分别在反比例函数与的图象上,
,,
解得,(正值舍去).
故答案为:.
16.3
解:如图,过作于
A,C的坐标分别是(0,2),(2,0),
故答案为:3
17.(1);(2);(3)步数之差最多是厘米,
解:(1)设反比例函数解析式为,
将,代入解析式得:,
解得:,
反比例函数解析式为;
(2)将代入得;
(3)反比例函数,
在每一象限随增大而减小,
当时,,
解得:,
当时,,
步数之差最多是厘米.
18.反比例函数的解析式为y=-.
解:∵将坐标原点O沿x轴向左平移2个单位长度得到点A,
∴OA=2,
∵AB//y轴,AB=,
∴B点坐标为:(-2,),
把B(-2,),代入y=中,得到k=-3,
∴反比例函数的解析式为y=-.
19.(1)
(2)存在,
解:(1)
点A(1,m),B(6,n)在反比例函数图象上,DC=5.
依题意,
解得
设反比例函数的解析式为,则
反比例函数的解析式为
(2)
存在,,理由如下,
如图,连接,设
,
,
,
解得
20.(1);(2)x<-1或0<x<3; (3)4.
解:(1)A(﹣1,m)代入y1=﹣x+2得m=1+2=3,∴A(-1,3),
将A点坐标(-1,3)代入,得,解得,k=-3
∴反比例函数的解析式为;
(2)易得,n=3,∴B(3,-1)
x<-1或0<x<3;
(3)如图,作AD成长x轴于点D,BE⊥x轴于点E,
则AD=3,BD=1,
易得,AB与x轴交点C(2,0),OC=2,
∴S△ABC=S△AOC+S△BOC=.
21.(1),;
(2)或;
(3);
(4)
(1)
解:把代入,得,
∴,
∵点在上,
∴,
∴,
把,代入得
,解得,
∴;
(2)
解:观察图象可知当或 ;
(3)
解:如图,
设与轴交于点,
∵点在直线上,
∴,
∴;
(4)
解:如图,
∵S△AOP:S△BOP=1:2,
∴,,
又,
∴点在第一象限,
∴,
又,
∴,解得,
把代入,得,
∴.
答案第1页,共2页
