人教版数学九年级下册 27.2相似三角形课件(共3课时) (共77张PPT)
文档属性
| 名称 | 人教版数学九年级下册 27.2相似三角形课件(共3课时) (共77张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 11:02:35 | ||
图片预览


文档简介
(共77张PPT)
第二十七章 相 似
27.2.1 相似三角形的判定(1)
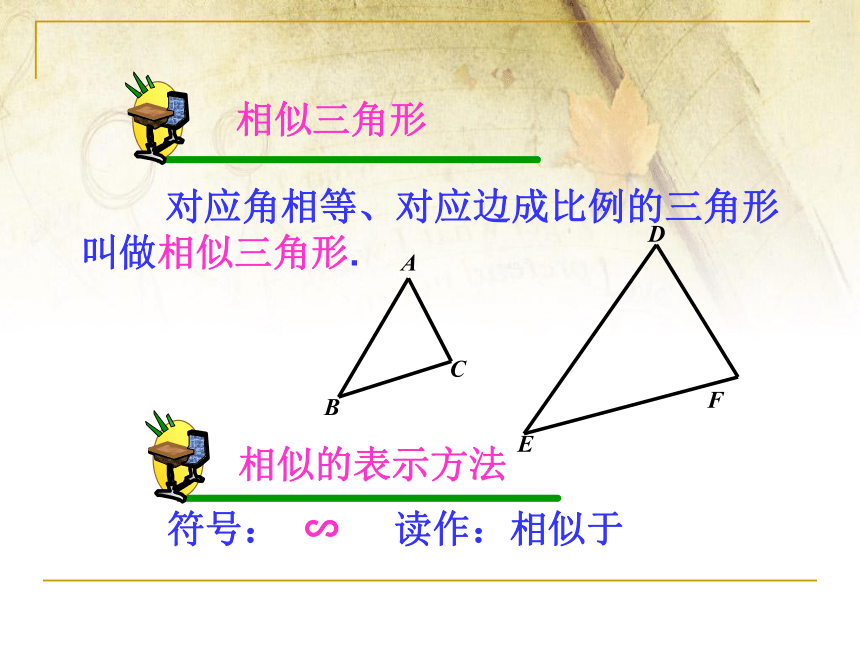
相似三角形
对应角相等、对应边成比例的三角形叫做相似三角形.
A
B
C
E
D
F
相似的表示方法
符号: ∽ 读作:相似于
A
B
C
A1
B1
C1
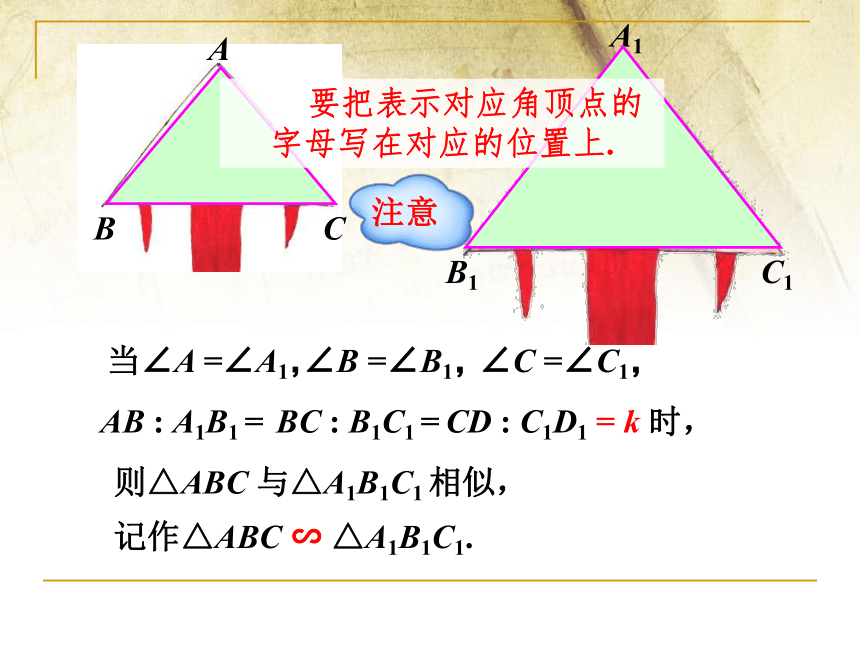
∠A =∠A1,
∠B =∠B1,
∠C =∠C1,
AB : A1B1 =
BC : B1C1 =
CD : C1D1
= k
当
时,
则△ABC 与△A1B1C1 相似,
记作△ABC ∽ △A1B1C1.
要把表示对应角顶点的字母写在对应的位置上.
注意
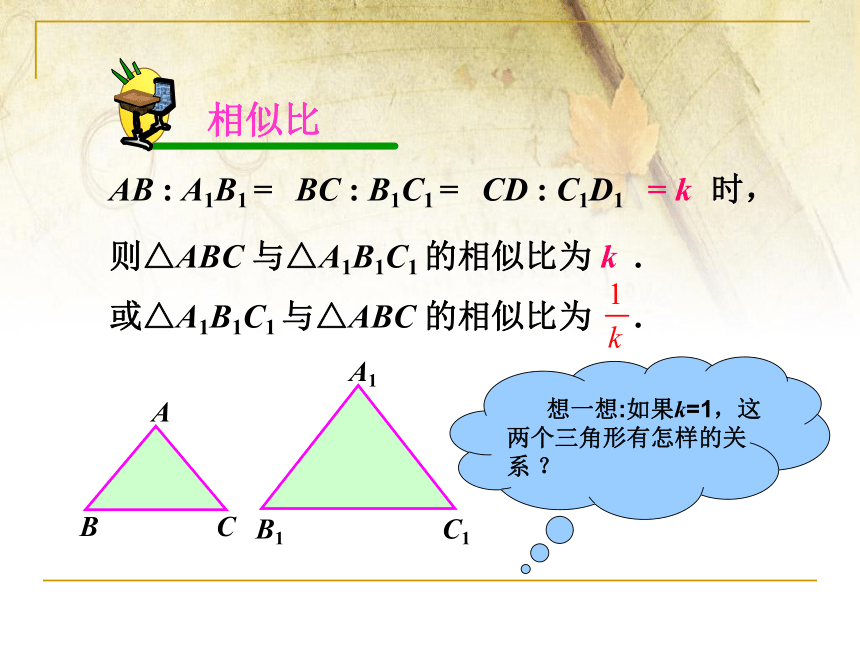
相似比
AB : A1B1 =
BC : B1C1 =
CD : C1D1
= k
时,
A
B
C
A1
B1
C1
则△ABC 与△A1B1C1 的相似比为 k .
或△A1B1C1 与△ABC 的相似比为 .
想一想:如果k=1,这两个三角形有怎样的关系 ?
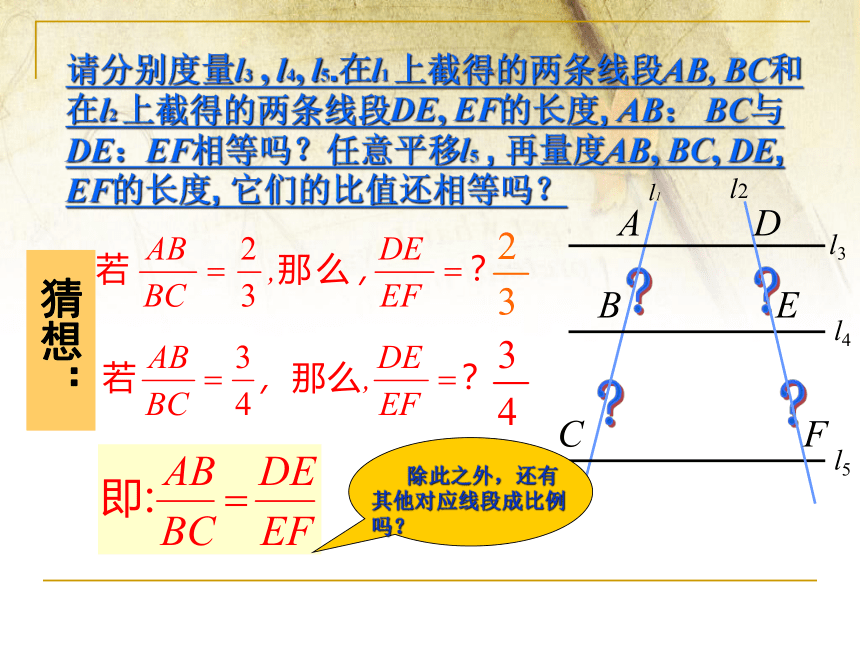
请分别度量l3 , l4, l5.在l1 上截得的两条线段AB, BC和在l2 上截得的两条线段DE, EF的长度, AB: BC与DE:EF相等吗?任意平移l5 , 再量度AB, BC, DE, EF的长度, 它们的比值还相等吗?
猜想:
A
B
C
D
E
F
l3
l4
l5
l1
l2
除此之外,还有其他对应线段成比例吗?
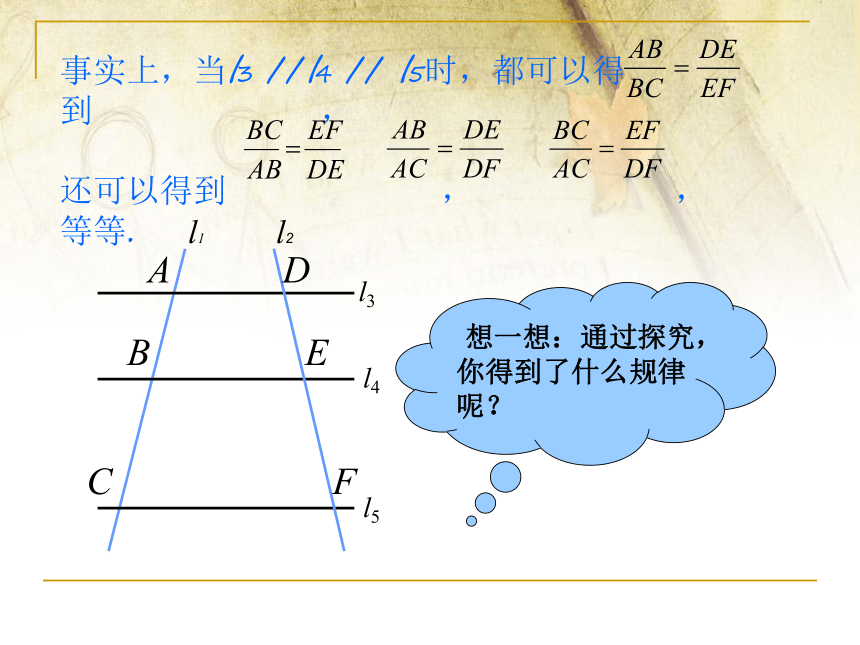
事实上,当l3 //l4 // l5时,都可以得到 ,
还可以得到 , , 等等.
A
B
C
D
E
F
l3
l4
l5
l1
l2
想一想:通过探究,你得到了什么规律呢?
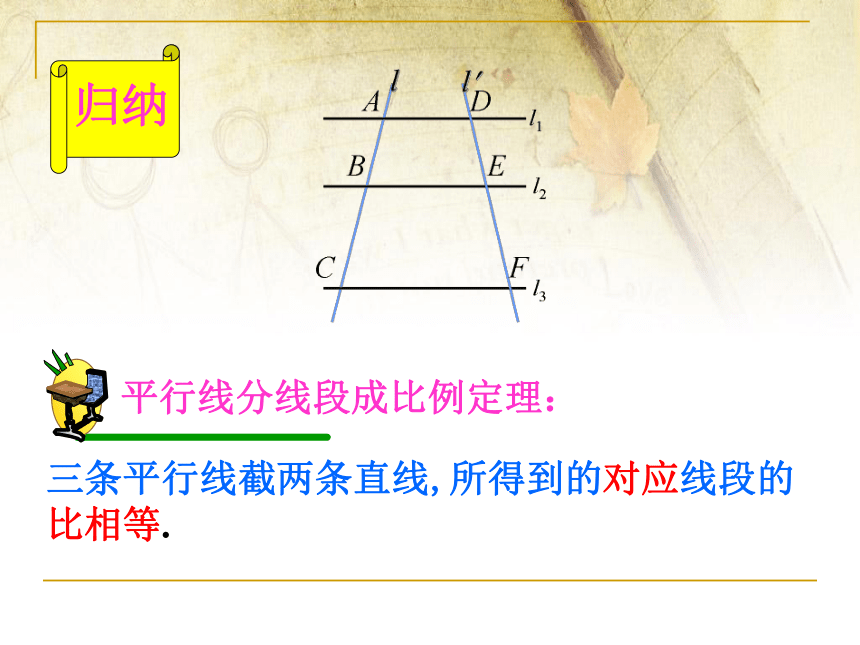
三条平行线截两条直线,所得到的对应线段的比相等.
归纳
平行线分线段成比例定理:
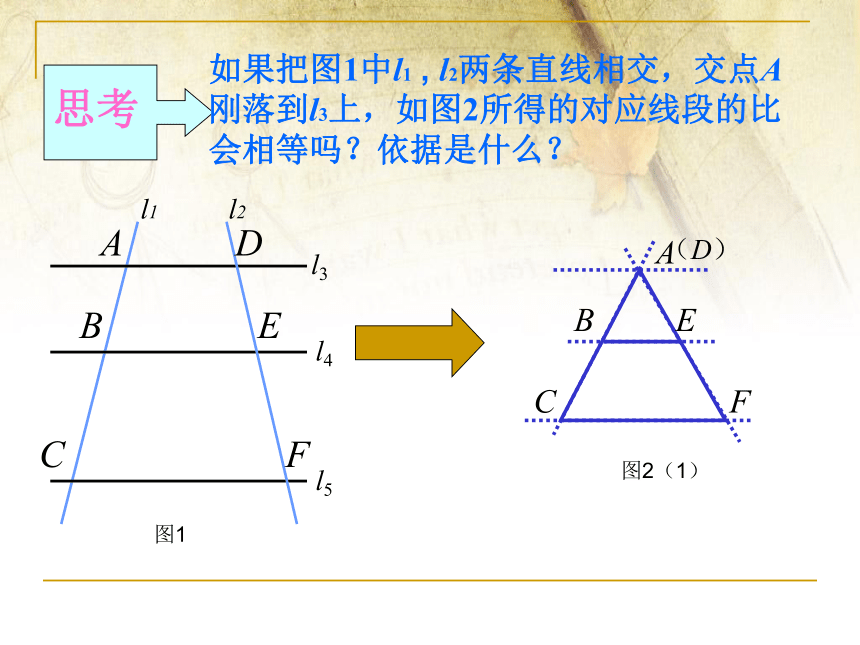
思考
如果把图1中l1 , l2两条直线相交,交点A刚落到l3上,如图2所得的对应线段的比会相等吗?依据是什么?
A
B
C
E
F
图2(1)
A
B
C
D
E
F
l3
l4
l5
l1
l2
(D)
图1
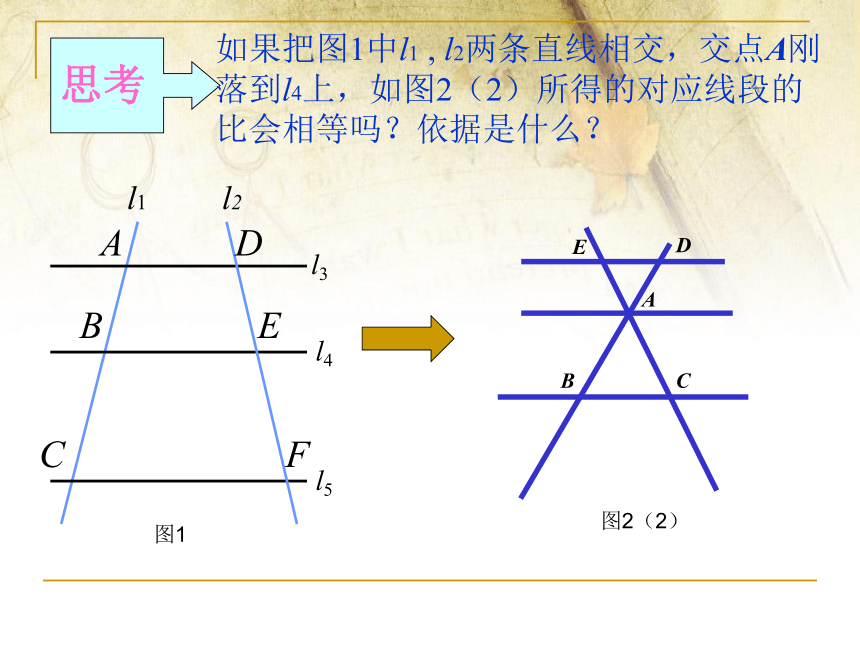
思考
如果把图1中l1 , l2两条直线相交,交点A刚落到l4上,如图2(2)所得的对应线段的比会相等吗?依据是什么?
A
B
C
D
E
F
l3
l4
l5
l1
l2
A
B
C
E
D
图1
图2(2)
l2
l3
l1
l3
l
l
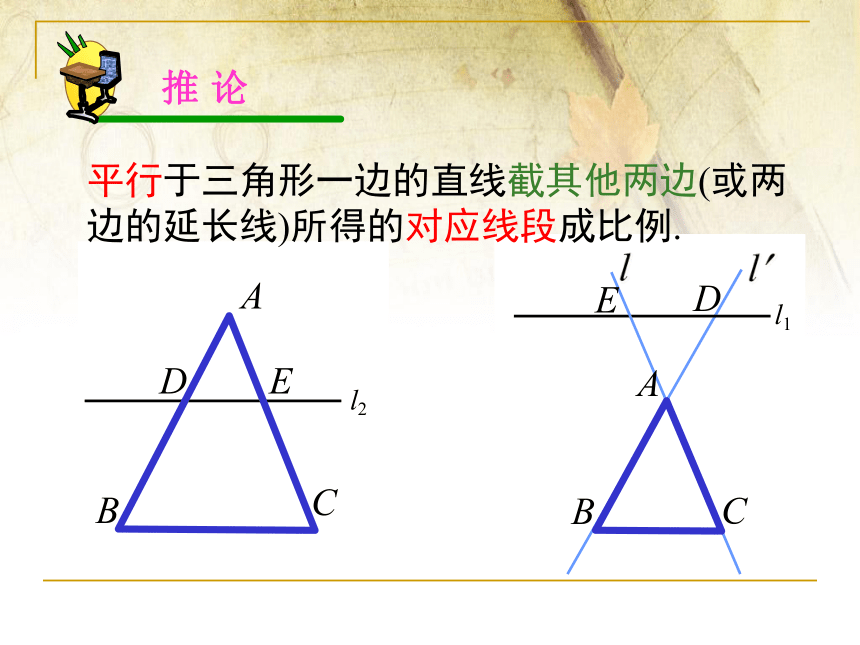
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
推 论
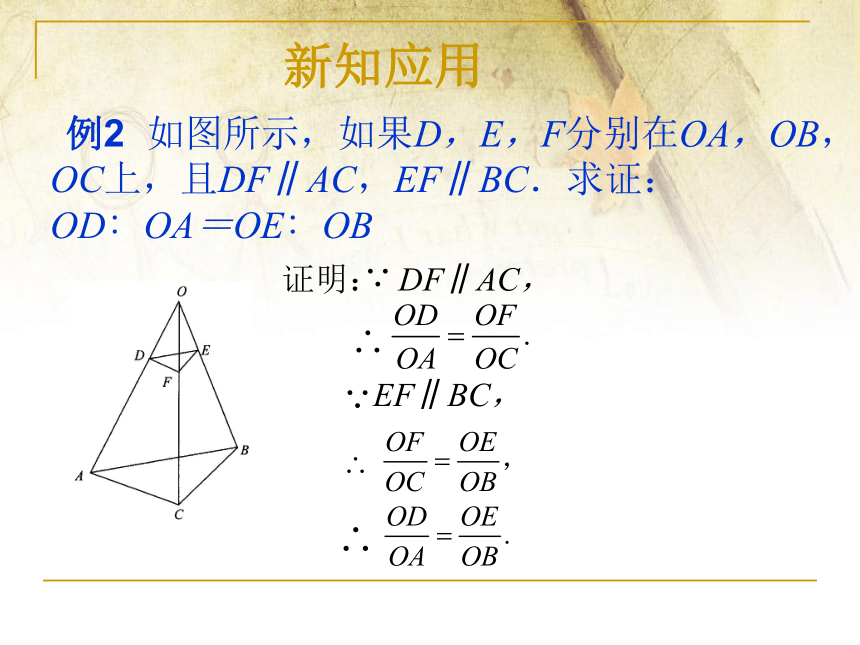
新知应用
例1 如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.
∴AE=3.
解∵AC=4,EC=1,
∵ DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
新知应用
例2 如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.求证:OD∶OA=OE∶OB
证明: DF∥AC,
EF∥BC,
一、平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例. (关键要能熟练地找出对应线段)
二、要熟悉该定理的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
课堂小结
三、注意该定理在三角形中的应用
拓展延伸,作业布置
如图,ΔABC中,BC=a.
(1)若AD1=
AB,AE1=
AC,则D1E1= ;
(2)若D1D2=
D1B,E1E2=
E1C,则D2E2= ;
D2B,E2E3=
E2C,则D3E3= ;……
Dn-1B,En-1En=
En-1C,则DnEn= .
(3)若D2D3=
(4)若Dn-1Dn=
不经历风雨,怎么见彩虹
没有人能随随便便成功!
第二十七章 相 似
27.2.1 相似三角形的判定(2)
三条平行线截两条直线,所得的对应线段的比相等.
平行线分线段成比例定理:
l2
l3
l1
l3
l
l
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
平行线分线段成比例定理的推论
如果△ ABC∽ △ADE,那么你能找出哪些角的关系?
∠A = ∠A,∠B = ∠ADE,∠C = ∠AED.
边呢?
A
D
E
B
C
=
=
DE ∥ BC
如图,在△ABC中, DE//BC, DE分别交AB于D,交AC于E ,△ADE与△ABC有什么关系 说明理由.
相似
A
B
C
D
E
证明:在△ADE与△ABC中,
∠A= ∠A.
∵ DE//BC,
∴∠ADE=∠B, ∠AED=∠C,
过E作EF//AB交BC于F,
∵ 四边形DBFE是平行四边形,
F
∴DE=BF,
∴△ADE∽△ABC.
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
知识要点
平行于三角形一边的定理
A
B
C
D
E
即在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC
A型
你还能画出其他图形吗?
归纳
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似.
D
E
O
C
B
延伸
即如果DE∥BC,
那么△ODE∽△OBC
你能证明吗?
X型
平行于三角形一边的直线与其他两边(或延长线)相交,所得的三角形与原三角形________.
相似
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
思考:有没有其他简单的办法判断两个三角形相似
任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论.
探究2
是否有△ABC∽△A′B′C′?
A
B
C
C′
B′
A′
三边对应成 比例
求证: △ .
∽△
A
B
C
D
E
∴
又
∴
同理
∴
∴
∥
∽
∽
∴
∽
∽
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
知识要点
判定三角形相似的定理之一
△ABC∽△A′B′C′.
即:
如果
那么
A′
B′
C′
A
B
C
三边对应成比例,两三角形相似.
边边边
S
S
S
√
归纳
改变k和∠A的值的大小,是否有同样的结论?
探究3
边角边
S
A
S
探究3
已知:
△ABC∽△A′B′ C′.
A′
B′
C′
A
B
C
求证:
∠A =∠A′ .
你能证明吗?
求证: △
∽△
A
B
C
D
E
∴
又
∴
∴
∴
∥
∽
∽
∴
∽
∽
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
知识要点
判定三角形相似的定理之二
两边对应成比例,且夹角相等,
两三角形相似.
边角边
S
A
S
√
A1
B1
C1
A
B
C
△ABC∽△A1B1C1.
即:
如果
∠B =∠B1 ,
那么
归纳
不会,因为不能证明构造的三角形和原三角形全等.
A
B
C
思考
如果
这两个三角形一定会相似吗?
应用
解:(1)
∽
两个三角形的相似比是多少?
应用
解:(2)
与
的三组对应边的比不等,它们不相似.
要使两个三角形相似,不改变AC的长,A′C′的长应改为多少?
例2 已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长.
解: AB=6,BC=4,AC=5,CD=
又∠B=∠ACD,
△ABC∽△DCA,
AD=
应用
相似三角形的判定方法有几种?
1.定义判定法
3.边边边判定法(SSS)
4.边角边判定法(SAS)
2.平行判定法
比较复杂,烦琐
只能在特定的图形里面使用
小结
27.2.1 相似三角形的判定(3)
平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似.
三边对应成比例,两三角形相似.
相似三角形的判定方法
两边对应成比例且夹角相等,两三角形相似.
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等.
观察你与老师的直角三角尺(30o与60o) ,会相似吗?
相
似
探究4
与同伴合作,一人先画△ABC,另一人再画△A′B′C′,使得∠A= ∠A′, ∠B= ∠B′.比较你们所画的两个三角形, ∠C= ∠C′ 吗?对应边之比
相等吗?这样的两个三角形相似吗?
改变这两个三角形边的大小,而不改它们角的大小呢?
如果两个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
知识要点
判定三角形相似的定理之三
两角对应相等,两三角形相似.
角角
A
A
A′
B′
C′
A
B
C
△ABC∽△ A′B′C′.
即
如果
那么
√
∠A =∠A ′ ,∠B =∠B ′ ,
在△ABC和△A′B′C′中,
角边角
A
S
A
角角边
A
A
S
角角
A
A
A1
B1
C1
A
B
C
已知:
△ABC∽△A1B1C1.
求证:
∠A =∠A1,∠B =∠B1 .
你能证明吗?
思考
已知:
△ABC∽△A1B1C1.
求证:
你能证明吗?可要仔细哟!
H
L
A
B
C
A1
B1
C1
Rt△ABC 和 Rt△A1B1C1,
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似.
判定三角形相似的定理之四
H
L
A
B
C
△ABC∽△A1B1C1.
即
如果
那么
√
A1
B1
C1
Rt△ABC 和 Rt△A1B1C1.
例1.弦AB和CD相交于⊙O内一点P.
求证:PA·PB=PC·PD.
A
B
C
D
P
O
证明:连接AC、BD.
∵∠A、∠D都是CB所对的圆周角,
⌒
∴ ∠A=∠D.
同理: ∠C=∠B.
∴△PAC∽△PDB.
即PA·PB=PC·PD.
新知应用
解: ∵ ∠ A= ∠ A,∠ABD=∠C,
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
∴ AB =4.
例2. 已知:如图,∠ABD=∠C,AD=2,
AC=8,求AB.
新知应用
在Rt△ABC的斜边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.
思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条?
我们来试一试…
课堂小结
相似图形三角形的判定方法:
通过定义
平行于三角形一边的直线
三边对应成比
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(SSS)
(AA)
(SAS)
(HL)
例1 已知左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部相距BD=5m.一个身高1.6m的人沿着正对这两棵树的一条水平直路m从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C
F
A
B
C
D
m
F
A
B
C
D
m
E
E
G
K
H
李巍同学在回家的 路上发现了如图两根电线杆AB、CD,分别在高10m的A处和15m的C处有两根钢索将两杆固定,求钢索AD与钢索BC的交点M离地面的高度MH.
H
Q
8
例2 如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0①求出面积S与时间t的关系式
B
C
D
P
A
6
H
┑
Q
8
例2 如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0①求出面积S与时间t的关系式
B
C
D
P
A
6
E
┓
②探究:在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。
Q
B
A
C
P
D
③探究:在P、Q两点移动的过程中,△CPQ 与△ABC能否相似?若能,求出此时点P的位置;若不能,请说明理由。
通过本堂课的学习和探索,
你学到了什么
老师的小结:
1、“数学建模”解决实际问题:
构造相似三角形解决实际生活中求线段长问题
2、“数学思想”解决综合题
“方程思想”
“分类讨论思想”
1.作业本(1) P13---14
2. 课时作业本 P54---55
作业分析
马戏团让狮子和公鸡表演跷跷板节目。跷跷板的支柱AB的高度为1.2m.
(1)若吊环高度为2m,支点A为跷跷板PQ的中点,则狮子能否将公鸡送到吊环上?为什么?
(2)若吊环高度为3.6m,在不改变其他条件的前提下移动支柱,当支点A移到跷跷板PQ什么位置时,狮子刚好将公鸡送到吊环上?
2、已知在△ABC中,∠C=90o ,AC=8cm,BC=6cm,点P从点A出发,沿AC以3cm/s的速度向点C移动,点Q从点B出发,沿BA以4cm/s的速度向点A移动。
如果P、Q分别从A、B 同时出发,移动时间为ts (0A
C
B
P
Q
Q
A
C
B
P
A
C
B
P
Q
回顾旧知
相似三角形有哪些性质?
A1
B1
C1
A
B
C
(1)相似三角形对应角相等。
(2)相似三角形对应边成比例。
(3)相似三角形对应高的比等于相似比。
(4)相似三角形对应中线的比等于相似比。
(5)相似三角形对应角平分线的比等于相似比。
相似三角形的性质
k
A1
B1
C1
A
B
C
相似三角形的周长有什么关系?
A1
B1
C1
A
B
C
相似三角形的面积有什么关系?
27.2.3 相似三角形的周长与面积
理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,并能用来解决简单的问题。
知识与能力
探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想。
过程与方法
经历探索相似三角形性质的过程,并在探究过程中发展学生积极的情感、态度、价值观,体验解决问题策略的多样性。
情感态度与价值观
教学重难点
理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方。
探索相似多边形周长的比等于相似比、面积比等于相似比的平方。
A1
B1
C1
A
B
C
(等比性质)
C△ABC = AB+BC+CA
周长:
C△A1B1C1 = A1B1+B1C1+C1A1
∵
∴
∴
相似三角形周长的比等于相似比。
六边形ABCDEF∽六边形A1B1C1D1E1F1,且相似比是k。
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
相似多边形周长的比等于相似比。
A1
B1
C1
A
B
C
S△ABC =
面积:
S△A1B1C1 =
∵
∴
∴
相似三角形面积的比等于相似比的平方。
D
D1
27.2.1中,我们知道对应高之比等于相似比。
S△ABC
S△A1B1C1
=
=
= k2
相似三角形面积的比等于相似比的平方。
同理:
课堂小结
对应角相等。
对应边成比例。
对应高的比等于相似比。
对应中线的比等于相似比。
对应角平分线的比等于相似比。
周长比等于相似比。
面积比等于相似比的平方。
相似三角形(多边形)的性质:
1. 已知两个三角形相似,请完成下列表格。
相似比
周长比
面积比
4
16
10
10
100
4
k
k
k2
随堂练习
2. 如果两个相似三角形的面积之比为1:9,则它们对应边的比为______,对应高的比为______ ,周长的比为______ 。
3. 如果两个相似三角形的面积之比为2:7,较大三角形一边上的高为7,则较小三角形对应边上的高为______ 。
1:3
1:3
1:3
4. 这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?
5. △ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,求△ABC的面积。
习题答案
1. 其他两边的实际长度都是20m.
2. (1)相似,因为对应边的比相等;
(2)不一定相似,因为相等的角的夹边的比不相等;
(3)相似,因为有两组对应角相等.
3. (1)相似;(2)相似,x=40.5,y=98.
第二十七章 相 似
27.2.1 相似三角形的判定(1)
相似三角形
对应角相等、对应边成比例的三角形叫做相似三角形.
A
B
C
E
D
F
相似的表示方法
符号: ∽ 读作:相似于
A
B
C
A1
B1
C1
∠A =∠A1,
∠B =∠B1,
∠C =∠C1,
AB : A1B1 =
BC : B1C1 =
CD : C1D1
= k
当
时,
则△ABC 与△A1B1C1 相似,
记作△ABC ∽ △A1B1C1.
要把表示对应角顶点的字母写在对应的位置上.
注意
相似比
AB : A1B1 =
BC : B1C1 =
CD : C1D1
= k
时,
A
B
C
A1
B1
C1
则△ABC 与△A1B1C1 的相似比为 k .
或△A1B1C1 与△ABC 的相似比为 .
想一想:如果k=1,这两个三角形有怎样的关系 ?
请分别度量l3 , l4, l5.在l1 上截得的两条线段AB, BC和在l2 上截得的两条线段DE, EF的长度, AB: BC与DE:EF相等吗?任意平移l5 , 再量度AB, BC, DE, EF的长度, 它们的比值还相等吗?
猜想:
A
B
C
D
E
F
l3
l4
l5
l1
l2
除此之外,还有其他对应线段成比例吗?
事实上,当l3 //l4 // l5时,都可以得到 ,
还可以得到 , , 等等.
A
B
C
D
E
F
l3
l4
l5
l1
l2
想一想:通过探究,你得到了什么规律呢?
三条平行线截两条直线,所得到的对应线段的比相等.
归纳
平行线分线段成比例定理:
思考
如果把图1中l1 , l2两条直线相交,交点A刚落到l3上,如图2所得的对应线段的比会相等吗?依据是什么?
A
B
C
E
F
图2(1)
A
B
C
D
E
F
l3
l4
l5
l1
l2
(D)
图1
思考
如果把图1中l1 , l2两条直线相交,交点A刚落到l4上,如图2(2)所得的对应线段的比会相等吗?依据是什么?
A
B
C
D
E
F
l3
l4
l5
l1
l2
A
B
C
E
D
图1
图2(2)
l2
l3
l1
l3
l
l
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
推 论
新知应用
例1 如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.
∴AE=3.
解∵AC=4,EC=1,
∵ DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
新知应用
例2 如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.求证:OD∶OA=OE∶OB
证明: DF∥AC,
EF∥BC,
一、平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例. (关键要能熟练地找出对应线段)
二、要熟悉该定理的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
课堂小结
三、注意该定理在三角形中的应用
拓展延伸,作业布置
如图,ΔABC中,BC=a.
(1)若AD1=
AB,AE1=
AC,则D1E1= ;
(2)若D1D2=
D1B,E1E2=
E1C,则D2E2= ;
D2B,E2E3=
E2C,则D3E3= ;……
Dn-1B,En-1En=
En-1C,则DnEn= .
(3)若D2D3=
(4)若Dn-1Dn=
不经历风雨,怎么见彩虹
没有人能随随便便成功!
第二十七章 相 似
27.2.1 相似三角形的判定(2)
三条平行线截两条直线,所得的对应线段的比相等.
平行线分线段成比例定理:
l2
l3
l1
l3
l
l
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
平行线分线段成比例定理的推论
如果△ ABC∽ △ADE,那么你能找出哪些角的关系?
∠A = ∠A,∠B = ∠ADE,∠C = ∠AED.
边呢?
A
D
E
B
C
=
=
DE ∥ BC
如图,在△ABC中, DE//BC, DE分别交AB于D,交AC于E ,△ADE与△ABC有什么关系 说明理由.
相似
A
B
C
D
E
证明:在△ADE与△ABC中,
∠A= ∠A.
∵ DE//BC,
∴∠ADE=∠B, ∠AED=∠C,
过E作EF//AB交BC于F,
∵ 四边形DBFE是平行四边形,
F
∴DE=BF,
∴△ADE∽△ABC.
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
知识要点
平行于三角形一边的定理
A
B
C
D
E
即在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC
A型
你还能画出其他图形吗?
归纳
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似.
D
E
O
C
B
延伸
即如果DE∥BC,
那么△ODE∽△OBC
你能证明吗?
X型
平行于三角形一边的直线与其他两边(或延长线)相交,所得的三角形与原三角形________.
相似
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
思考:有没有其他简单的办法判断两个三角形相似
任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论.
探究2
是否有△ABC∽△A′B′C′?
A
B
C
C′
B′
A′
三边对应成 比例
求证: △ .
∽△
A
B
C
D
E
∴
又
∴
同理
∴
∴
∥
∽
∽
∴
∽
∽
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
知识要点
判定三角形相似的定理之一
△ABC∽△A′B′C′.
即:
如果
那么
A′
B′
C′
A
B
C
三边对应成比例,两三角形相似.
边边边
S
S
S
√
归纳
改变k和∠A的值的大小,是否有同样的结论?
探究3
边角边
S
A
S
探究3
已知:
△ABC∽△A′B′ C′.
A′
B′
C′
A
B
C
求证:
∠A =∠A′ .
你能证明吗?
求证: △
∽△
A
B
C
D
E
∴
又
∴
∴
∴
∥
∽
∽
∴
∽
∽
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
知识要点
判定三角形相似的定理之二
两边对应成比例,且夹角相等,
两三角形相似.
边角边
S
A
S
√
A1
B1
C1
A
B
C
△ABC∽△A1B1C1.
即:
如果
∠B =∠B1 ,
那么
归纳
不会,因为不能证明构造的三角形和原三角形全等.
A
B
C
思考
如果
这两个三角形一定会相似吗?
应用
解:(1)
∽
两个三角形的相似比是多少?
应用
解:(2)
与
的三组对应边的比不等,它们不相似.
要使两个三角形相似,不改变AC的长,A′C′的长应改为多少?
例2 已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长.
解: AB=6,BC=4,AC=5,CD=
又∠B=∠ACD,
△ABC∽△DCA,
AD=
应用
相似三角形的判定方法有几种?
1.定义判定法
3.边边边判定法(SSS)
4.边角边判定法(SAS)
2.平行判定法
比较复杂,烦琐
只能在特定的图形里面使用
小结
27.2.1 相似三角形的判定(3)
平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似.
三边对应成比例,两三角形相似.
相似三角形的判定方法
两边对应成比例且夹角相等,两三角形相似.
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等.
观察你与老师的直角三角尺(30o与60o) ,会相似吗?
相
似
探究4
与同伴合作,一人先画△ABC,另一人再画△A′B′C′,使得∠A= ∠A′, ∠B= ∠B′.比较你们所画的两个三角形, ∠C= ∠C′ 吗?对应边之比
相等吗?这样的两个三角形相似吗?
改变这两个三角形边的大小,而不改它们角的大小呢?
如果两个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
知识要点
判定三角形相似的定理之三
两角对应相等,两三角形相似.
角角
A
A
A′
B′
C′
A
B
C
△ABC∽△ A′B′C′.
即
如果
那么
√
∠A =∠A ′ ,∠B =∠B ′ ,
在△ABC和△A′B′C′中,
角边角
A
S
A
角角边
A
A
S
角角
A
A
A1
B1
C1
A
B
C
已知:
△ABC∽△A1B1C1.
求证:
∠A =∠A1,∠B =∠B1 .
你能证明吗?
思考
已知:
△ABC∽△A1B1C1.
求证:
你能证明吗?可要仔细哟!
H
L
A
B
C
A1
B1
C1
Rt△ABC 和 Rt△A1B1C1,
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似.
判定三角形相似的定理之四
H
L
A
B
C
△ABC∽△A1B1C1.
即
如果
那么
√
A1
B1
C1
Rt△ABC 和 Rt△A1B1C1.
例1.弦AB和CD相交于⊙O内一点P.
求证:PA·PB=PC·PD.
A
B
C
D
P
O
证明:连接AC、BD.
∵∠A、∠D都是CB所对的圆周角,
⌒
∴ ∠A=∠D.
同理: ∠C=∠B.
∴△PAC∽△PDB.
即PA·PB=PC·PD.
新知应用
解: ∵ ∠ A= ∠ A,∠ABD=∠C,
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
∴ AB =4.
例2. 已知:如图,∠ABD=∠C,AD=2,
AC=8,求AB.
新知应用
在Rt△ABC的斜边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.
思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条?
我们来试一试…
课堂小结
相似图形三角形的判定方法:
通过定义
平行于三角形一边的直线
三边对应成比
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(SSS)
(AA)
(SAS)
(HL)
例1 已知左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部相距BD=5m.一个身高1.6m的人沿着正对这两棵树的一条水平直路m从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C
F
A
B
C
D
m
F
A
B
C
D
m
E
E
G
K
H
李巍同学在回家的 路上发现了如图两根电线杆AB、CD,分别在高10m的A处和15m的C处有两根钢索将两杆固定,求钢索AD与钢索BC的交点M离地面的高度MH.
H
Q
8
例2 如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0
B
C
D
P
A
6
H
┑
Q
8
例2 如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0
B
C
D
P
A
6
E
┓
②探究:在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。
Q
B
A
C
P
D
③探究:在P、Q两点移动的过程中,△CPQ 与△ABC能否相似?若能,求出此时点P的位置;若不能,请说明理由。
通过本堂课的学习和探索,
你学到了什么
老师的小结:
1、“数学建模”解决实际问题:
构造相似三角形解决实际生活中求线段长问题
2、“数学思想”解决综合题
“方程思想”
“分类讨论思想”
1.作业本(1) P13---14
2. 课时作业本 P54---55
作业分析
马戏团让狮子和公鸡表演跷跷板节目。跷跷板的支柱AB的高度为1.2m.
(1)若吊环高度为2m,支点A为跷跷板PQ的中点,则狮子能否将公鸡送到吊环上?为什么?
(2)若吊环高度为3.6m,在不改变其他条件的前提下移动支柱,当支点A移到跷跷板PQ什么位置时,狮子刚好将公鸡送到吊环上?
2、已知在△ABC中,∠C=90o ,AC=8cm,BC=6cm,点P从点A出发,沿AC以3cm/s的速度向点C移动,点Q从点B出发,沿BA以4cm/s的速度向点A移动。
如果P、Q分别从A、B 同时出发,移动时间为ts (0
C
B
P
Q
Q
A
C
B
P
A
C
B
P
Q
回顾旧知
相似三角形有哪些性质?
A1
B1
C1
A
B
C
(1)相似三角形对应角相等。
(2)相似三角形对应边成比例。
(3)相似三角形对应高的比等于相似比。
(4)相似三角形对应中线的比等于相似比。
(5)相似三角形对应角平分线的比等于相似比。
相似三角形的性质
k
A1
B1
C1
A
B
C
相似三角形的周长有什么关系?
A1
B1
C1
A
B
C
相似三角形的面积有什么关系?
27.2.3 相似三角形的周长与面积
理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,并能用来解决简单的问题。
知识与能力
探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想。
过程与方法
经历探索相似三角形性质的过程,并在探究过程中发展学生积极的情感、态度、价值观,体验解决问题策略的多样性。
情感态度与价值观
教学重难点
理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方。
探索相似多边形周长的比等于相似比、面积比等于相似比的平方。
A1
B1
C1
A
B
C
(等比性质)
C△ABC = AB+BC+CA
周长:
C△A1B1C1 = A1B1+B1C1+C1A1
∵
∴
∴
相似三角形周长的比等于相似比。
六边形ABCDEF∽六边形A1B1C1D1E1F1,且相似比是k。
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
相似多边形周长的比等于相似比。
A1
B1
C1
A
B
C
S△ABC =
面积:
S△A1B1C1 =
∵
∴
∴
相似三角形面积的比等于相似比的平方。
D
D1
27.2.1中,我们知道对应高之比等于相似比。
S△ABC
S△A1B1C1
=
=
= k2
相似三角形面积的比等于相似比的平方。
同理:
课堂小结
对应角相等。
对应边成比例。
对应高的比等于相似比。
对应中线的比等于相似比。
对应角平分线的比等于相似比。
周长比等于相似比。
面积比等于相似比的平方。
相似三角形(多边形)的性质:
1. 已知两个三角形相似,请完成下列表格。
相似比
周长比
面积比
4
16
10
10
100
4
k
k
k2
随堂练习
2. 如果两个相似三角形的面积之比为1:9,则它们对应边的比为______,对应高的比为______ ,周长的比为______ 。
3. 如果两个相似三角形的面积之比为2:7,较大三角形一边上的高为7,则较小三角形对应边上的高为______ 。
1:3
1:3
1:3
4. 这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?
5. △ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,求△ABC的面积。
习题答案
1. 其他两边的实际长度都是20m.
2. (1)相似,因为对应边的比相等;
(2)不一定相似,因为相等的角的夹边的比不相等;
(3)相似,因为有两组对应角相等.
3. (1)相似;(2)相似,x=40.5,y=98.
