6.1 分类加法计数原理与分步乘法计数原理 应用课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(15张ppt)
文档属性
| 名称 | 6.1 分类加法计数原理与分步乘法计数原理 应用课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(15张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 554.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 15:42:25 | ||
图片预览






文档简介
(共15张PPT)
2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册
6.1分类加法计数原理与分步乘法计数原理应用课件(1)
一、学习目标(1分钟)
学习两种基本计数原理灵活运用
1、分类加法计数原理概念理解、应用几种常见题型处理
2、分步乘法计数原理概念理解、应用几种常见题型处理
二、问题导学(3分钟)
知识点一 分类加法计数原理
完成一件事有n类不同的方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,则完成这件事共有N=____________________种不同的方法.
m1+m2+…+mn
知识点二 分步乘法计数原理
完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,
……,做第n步有mn种不同的方法,则完成这件事共有N=____________种不同的方法
m1×m2×…×mn
三、点拨精讲(28分钟)
例1:若x,y∈N*,且x+y≤6,试求有序自然数对(x,y)的个数.
解:按x的取值进行分类:
x=1时,y=1,2,3,4,5,共构成5个有序自然数对;
x=2时,y=1,2,3,4,共构成4个有序自然数对;
……
x=5时,y=1,共构成1个有序自然数对.
根据分类加法计数原理,共有N=5+4+3+2+1=15个有序自然数对.
知识点一 分类加法计数原理
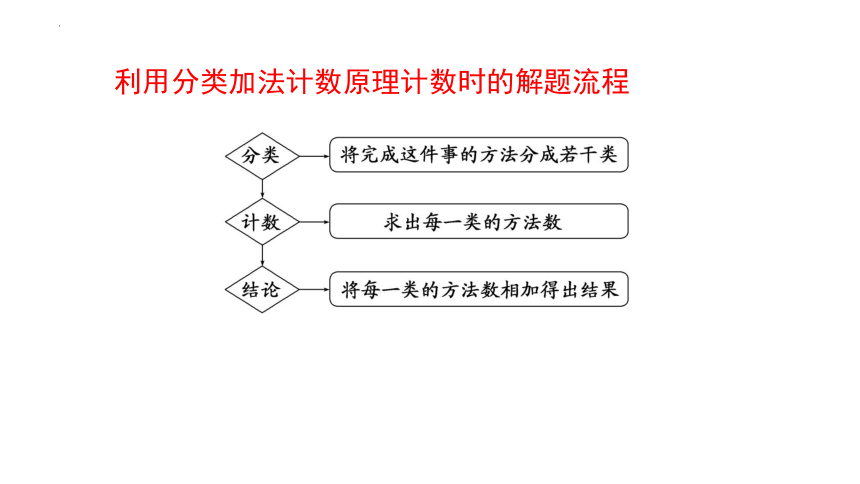
利用分类加法计数原理计数时的解题流程
例2:某艺术小组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,
3人会小号,从中选出会钢琴和会小号的各1人,有多少种不同的选法?
[解析] 由题意知,在艺术小组9人中,有且仅有1人既会钢琴又会小号(称为“多面手”),只会钢琴的有6人,只会小号的有2人.按“多面手”的选法分为两类:
(1)“多面手”入选,则有6+2=8(种)选法;
(2)“多面手”不入选,则有6×2=12(种)选法.
因此选法共有8+12=20(种).
例3:如图,一环形花坛分成A、B、C、D四个区域,现有4种不同的花供选种,要求在每个区域里种1种花,且相邻的2个区域种不同的花,则不同的种法种数为( )
A.96 B.84
C.60 D.48
[解析] A有4种不同种法;
B有3种不同种法;
对于C可分为两类,若C与A种相同的花,则D有3种不同种法;若C与A种不同的花,则C有3种不同种法,D也有2种不同种法.
所以共有4×3×(3+2×2)=84(种)不同的种法.故选B.
例4:从1,2,3,4中选三个数字,组成无重复数字的整数,则满足下列条件的数有多少个?
(1)三位数; (2)三位偶数.
知识点二 分步乘法计数原理
[解] (1)三位数有三个数位:
故可分三个步骤完成:
第1步,排个位,从1,2,3,4中选1个数字,有4种方法;
第2步,排十位,从剩下的3个数字中选1个,有3种方法;
第3步,排百位,从剩下的2个数字中选1个,有2种方法.
根据分步乘法计数原理,共有4×3×2=24个满足要求的三位数.
(2)分三个步骤完成:
第1步,排个位,从2,4中选1个,有2种方法;
第2步,排十位,从余下的3个数字中选1个,有3种方法;
第3步,排百位,只能从余下的2个数字中选1个,有2种方法.
根据分步乘法计数原理,共有2×3×2=12个满足要求的三位偶数.
利用分步乘法计数原理计数时的解题流程
例5:一个口袋里有5封信,另一个口袋里有4封信,各封信内容均不相同.
(1)从两个口袋里各取1封信,有多少种不同的取法?
(2)把这两个口袋里的9封信,分别投入4个邮筒,有多少种不同的投法?
解:(1)各取1封信,不论从哪个口袋里取,都不能算完成了这件事,因此应分两个步骤完成,由分步乘法计数原理知,共有5×4=20种不同的取法.
(2)若从每封信投入邮筒的可能性考虑,第1封信投入邮筒有4种可能,第2封信仍有4种可能……第9封信还有4种可能,所以共有49种不同的投法.
例6:有一项活动,需在3名老师、8名男同学和5名女同学中选部分人员参加.
(1)若只需一人参加,有多少种不同的选法?
(2)若需老师、男同学、女同学各一人参加,有多少种不同的选法?
(3)若需一名老师、一名同学参加,有多少种不同的选法?
解:(1)有三类:3名老师中选一人,有3种方法;8名男同学中选一人,有8种方法;5名女同学中选一人,有5种方法.由分类加法计数原理知,有3+8+5=16种选法.
(2)分三步:第1步选老师,有3种方法;第2步选男同学,有8种方法;第3步选女同学,有5种方法.
由分步乘法计数原理知,共有3×8×5=120种选法.
(3)可分两类,每一类又分两步.
第1类,选一名老师再选一名男同学,有3×8=24种选法;
第2类,选一名老师再选一名女同学,共有3×5=15种选法.
由分类加法计数原理知,共有24+15=39种选法.
例7:有红、黄、蓝旗各3面,每次升1面、2面或3面旗纵向排列在某一旗杆上,表示不同的信号,顺序不同也表示不同的信号,共可以组成多少种不同的信号?
[解]每次升1面旗可组成3种不同的信号;每次升2面旗可组成3×3=9种
不同的信号;每次升3面旗可组成3×3×3=27种不同的信号.根据分类加法
计数原理,共可组成3+9+27=39种不同的信号.
解题小结:
1.求解时,易忽略信号可分为每次升1面、每次升2面、每次升3面这三类.
2.解决此类问题一般是先分类再分步,分类时要设计好标准,设计好分类方案,防止重复和遗漏,分步时要注意步与步之间的连续性.
例8:某外语小组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,
从中选出会英语和日语的各一人组成一个二人活动小组,有多少种不同的选法?
解:共分三类:第1类,当既会英语又会日语的人被当作会英语的人时,
选出只会日语的一人即可,有2种选法;
第2类,既会英语又会日语的人被当作会日语的人时,
选出只会英语的一人即可,有6种选法;
第3类,既会英语又会日语的人都不参加该二人组时,
则需从只会日语和只会英语的人中各选一人,有2×6=12种方法,
故共有2+6+12=20种选法.
四、课堂小结(1分钟)
1.理解分类加法计数原理与分步乘法计数原理.
2.会利用两个基本原理分析和解决一些简单的实际问题.
3.用两个计数原理解决计数问题时,开始要进行分析——需分类还是分步.分类要“不重不漏”,分步要“步骤完整”.分类用加法,分步用乘法.有的试题中经常出现“类中有步,步中有类”的情况.
五、当堂检测(12分钟)
练习1:将红、黄、绿、黑四种不同的颜色涂入图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?
72种
2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册
6.1分类加法计数原理与分步乘法计数原理应用课件(1)
一、学习目标(1分钟)
学习两种基本计数原理灵活运用
1、分类加法计数原理概念理解、应用几种常见题型处理
2、分步乘法计数原理概念理解、应用几种常见题型处理
二、问题导学(3分钟)
知识点一 分类加法计数原理
完成一件事有n类不同的方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,则完成这件事共有N=____________________种不同的方法.
m1+m2+…+mn
知识点二 分步乘法计数原理
完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,
……,做第n步有mn种不同的方法,则完成这件事共有N=____________种不同的方法
m1×m2×…×mn
三、点拨精讲(28分钟)
例1:若x,y∈N*,且x+y≤6,试求有序自然数对(x,y)的个数.
解:按x的取值进行分类:
x=1时,y=1,2,3,4,5,共构成5个有序自然数对;
x=2时,y=1,2,3,4,共构成4个有序自然数对;
……
x=5时,y=1,共构成1个有序自然数对.
根据分类加法计数原理,共有N=5+4+3+2+1=15个有序自然数对.
知识点一 分类加法计数原理
利用分类加法计数原理计数时的解题流程
例2:某艺术小组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,
3人会小号,从中选出会钢琴和会小号的各1人,有多少种不同的选法?
[解析] 由题意知,在艺术小组9人中,有且仅有1人既会钢琴又会小号(称为“多面手”),只会钢琴的有6人,只会小号的有2人.按“多面手”的选法分为两类:
(1)“多面手”入选,则有6+2=8(种)选法;
(2)“多面手”不入选,则有6×2=12(种)选法.
因此选法共有8+12=20(种).
例3:如图,一环形花坛分成A、B、C、D四个区域,现有4种不同的花供选种,要求在每个区域里种1种花,且相邻的2个区域种不同的花,则不同的种法种数为( )
A.96 B.84
C.60 D.48
[解析] A有4种不同种法;
B有3种不同种法;
对于C可分为两类,若C与A种相同的花,则D有3种不同种法;若C与A种不同的花,则C有3种不同种法,D也有2种不同种法.
所以共有4×3×(3+2×2)=84(种)不同的种法.故选B.
例4:从1,2,3,4中选三个数字,组成无重复数字的整数,则满足下列条件的数有多少个?
(1)三位数; (2)三位偶数.
知识点二 分步乘法计数原理
[解] (1)三位数有三个数位:
故可分三个步骤完成:
第1步,排个位,从1,2,3,4中选1个数字,有4种方法;
第2步,排十位,从剩下的3个数字中选1个,有3种方法;
第3步,排百位,从剩下的2个数字中选1个,有2种方法.
根据分步乘法计数原理,共有4×3×2=24个满足要求的三位数.
(2)分三个步骤完成:
第1步,排个位,从2,4中选1个,有2种方法;
第2步,排十位,从余下的3个数字中选1个,有3种方法;
第3步,排百位,只能从余下的2个数字中选1个,有2种方法.
根据分步乘法计数原理,共有2×3×2=12个满足要求的三位偶数.
利用分步乘法计数原理计数时的解题流程
例5:一个口袋里有5封信,另一个口袋里有4封信,各封信内容均不相同.
(1)从两个口袋里各取1封信,有多少种不同的取法?
(2)把这两个口袋里的9封信,分别投入4个邮筒,有多少种不同的投法?
解:(1)各取1封信,不论从哪个口袋里取,都不能算完成了这件事,因此应分两个步骤完成,由分步乘法计数原理知,共有5×4=20种不同的取法.
(2)若从每封信投入邮筒的可能性考虑,第1封信投入邮筒有4种可能,第2封信仍有4种可能……第9封信还有4种可能,所以共有49种不同的投法.
例6:有一项活动,需在3名老师、8名男同学和5名女同学中选部分人员参加.
(1)若只需一人参加,有多少种不同的选法?
(2)若需老师、男同学、女同学各一人参加,有多少种不同的选法?
(3)若需一名老师、一名同学参加,有多少种不同的选法?
解:(1)有三类:3名老师中选一人,有3种方法;8名男同学中选一人,有8种方法;5名女同学中选一人,有5种方法.由分类加法计数原理知,有3+8+5=16种选法.
(2)分三步:第1步选老师,有3种方法;第2步选男同学,有8种方法;第3步选女同学,有5种方法.
由分步乘法计数原理知,共有3×8×5=120种选法.
(3)可分两类,每一类又分两步.
第1类,选一名老师再选一名男同学,有3×8=24种选法;
第2类,选一名老师再选一名女同学,共有3×5=15种选法.
由分类加法计数原理知,共有24+15=39种选法.
例7:有红、黄、蓝旗各3面,每次升1面、2面或3面旗纵向排列在某一旗杆上,表示不同的信号,顺序不同也表示不同的信号,共可以组成多少种不同的信号?
[解]每次升1面旗可组成3种不同的信号;每次升2面旗可组成3×3=9种
不同的信号;每次升3面旗可组成3×3×3=27种不同的信号.根据分类加法
计数原理,共可组成3+9+27=39种不同的信号.
解题小结:
1.求解时,易忽略信号可分为每次升1面、每次升2面、每次升3面这三类.
2.解决此类问题一般是先分类再分步,分类时要设计好标准,设计好分类方案,防止重复和遗漏,分步时要注意步与步之间的连续性.
例8:某外语小组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,
从中选出会英语和日语的各一人组成一个二人活动小组,有多少种不同的选法?
解:共分三类:第1类,当既会英语又会日语的人被当作会英语的人时,
选出只会日语的一人即可,有2种选法;
第2类,既会英语又会日语的人被当作会日语的人时,
选出只会英语的一人即可,有6种选法;
第3类,既会英语又会日语的人都不参加该二人组时,
则需从只会日语和只会英语的人中各选一人,有2×6=12种方法,
故共有2+6+12=20种选法.
四、课堂小结(1分钟)
1.理解分类加法计数原理与分步乘法计数原理.
2.会利用两个基本原理分析和解决一些简单的实际问题.
3.用两个计数原理解决计数问题时,开始要进行分析——需分类还是分步.分类要“不重不漏”,分步要“步骤完整”.分类用加法,分步用乘法.有的试题中经常出现“类中有步,步中有类”的情况.
五、当堂检测(12分钟)
练习1:将红、黄、绿、黑四种不同的颜色涂入图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?
72种
