6.1分类加法计数原理与分步乘法计数原理课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(16张ppt)
文档属性
| 名称 | 6.1分类加法计数原理与分步乘法计数原理课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 473.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 16:08:47 | ||
图片预览






文档简介
(共16张PPT)
2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册
6.1分类加法计数原理与分步乘法计数原理课件
一、学习目标(1分钟)
学习两种基本计数原理
1、分类加法计数原理概念理解、应用理解
2、分步乘法计数原理概念理解、应用理解
二、问题导学(3分钟)
2022年3月4日政协十三届五次会议在北京人民大会堂举行,某政协委员3月2日要从湖北前往北京参加会议.他有两类快捷途径可供选择:一是乘飞机,二是乘坐动车组.假如这天飞机有3个航班可乘,动车组有4个班次可乘.
问:此委员这一天从湖北到北京共有多少种快捷途径可选?
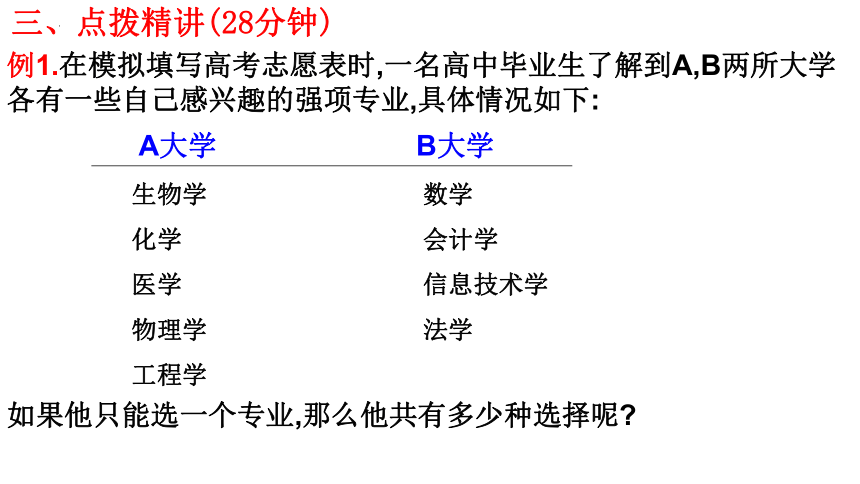
例1.在模拟填写高考志愿表时,一名高中毕业生了解到A,B两所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学
B大学
生物学
化学
医学
物理学
工程学
数学
会计学
信息技术学
法学
如果他只能选一个专业,那么他共有多少种选择呢
三、点拨精讲(28分钟)
[分析] 由于这名同学在A,B两所大学中只能选择一所,而且只能选择一个专业,又由于两所大学没有共同的强项专业,因此符合分类加法计数原理的条件.
[解析] 这名同学可以选择A,B两所大学的一所,在A大学中有5种专业选择方法,在B大学中有4种专业选择方法,又由于没有一个强项专业是两所大学共有的,因此根据分类加法计数原理,这名同学可能的专业选择共有5+4=9(种).
[方法总结] 使用分类加法计数原理时,要根据问题的特点确定一个分类的标准.
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法.
分类加法计数原理
推广 完成一件事,有n类不同方案.在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,则完成这件事共有 N= m1+ m2+ ……+ mn种不同的方法.
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法.
分类加法计数原理
2.分类标准清晰,不重不漏;
1.各方法能独立的完成这件事;
3.可推广到n类.
变式:某班有男生26人,女生24人,从中选一位同学为数学课代表,则不同选法的种数是( )
A.50 B.26
C.24 D.616
[答案] A
[解析] 选一位同学或者选男生,或者选女生,用加法原理完成.
三、点拨精讲(28分钟)
例2:设某班有男生30名,女生24名.现要从中选出男、女生各
一名代表班级参加比赛,共有多少种不同的选法?
[解析] 第一步,从30名男生中选出1人,有30种不同的选法;
第二步,从24名女生中选出1人,有24种不同的选法.
根据分步乘法计数原理,共有30×24=720种不同的选法.
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法.
分步乘法计数原理
推广 完成一件事,需要分成n个步骤.做第1步有有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,则完成这件事共有 N= m1× m2× ……× mn种不同的方法.
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法.
分步乘法计数原理
1.各步相互依存, 每步都完成才算完成此事;
2.分步标准清晰 ;
3.可推广到n步.
1、4名同学去争夺3项冠军,不允许并列,共有多少种不同的情况?
[错解] 错解1:第一步,第1位同学去夺这3项冠军,有可能1项都不夺或夺1项、2项、3项,因此有4种不同的情况;
第二步,第2位同学去夺这3项冠军也有4种不同的情况;
第二步,第2位同学去夺这3项冠军也有4种不同的情况;
同理第3位、第4位同学也各有4种不同的情况.
由分步乘法计数原理,共有4×4×4×4=44=256种不同的情况.
易错疑难辨析
错解2:第一步,第1位同学去争冠军,有3种不同的情况;
第二步,第2位同学去争冠军,也有3种不同的情况;
同理第3位、第4位同学也各有3种不同的情况.
由分步乘法计算原理,共有3×3×3×3=34=81种不同的情况.
[辨析] 完成夺取冠军这件事,即每项冠军都有人夺取.错解1中可能有4位同学都不得冠军以及1项冠军不止1人获得这种情况,与题意不符;错解2中可能有1项冠军不止1人获得这种情况,也不符合题意.
[正解] 可分三步完成,第一项冠军被4名同学争夺,一定是其中1名而且只能是其中一名同学获得,共有4种不同的情况;同理其余2项冠军分被4名同学中的1名获得,各有4种不同的情况.由分步乘法计算原理,共有4×4×4=43=64种不同的夺得冠军的情况.
分类加法计数原理 分步乘法计数原理
相同点
不同点
注意点
用来计算“完成一件事”的方法种数
每类方案中的每一种方法都能______ 完成这件事
每步_________才算完成这件事情
(每步中的每一种方法不能独立完成这件事)
类类相加
步步相乘
类类独立
步步相依
独立
依次完成
不重不漏
步骤完整
分类完成
分步完成
四、课堂小结(1分钟)
五、当堂检测(12分钟)
练1:现有高一四个班学生34个,其中一、二、三、四班各7人、8人、9人、10人,他们自愿组成数学课外小组.
(1)选其中一人为负责人,有多少种不同的选法?
(2)每班选一名组长,有多少种不同的选法?
(3)推选二人作中心发言,这二人需来自不同的班级,有多少种不同的选法?
[分析] (1)是从四个班的34人中选一人,应分类求解,
(2)是从各班中选一人,共选4人,应分步求解,
(3)是先根据不同班级分类,再分步从两个班级中各选1人.
[解析] (1)分四类,第一类,从一班学生中选1人,有7种选法;第二类,从二班学生中选1人,有8种选法;第三类,从三班学生中选1人,有9种选法;第四类,从四班学生中选1人,有10种选法,所以,共有不同的选法N=7+8+9+10=34种.
(2)分四步,第一、二、三、四步分别从一、二、三、四班学生中选一人任组长,所以共有不同的选法N=7×8×9×10=5 040种.
(3)分六类,每类又分两步;从一班、二班学生中各选1人,有7×8种不同的选法;从一、三班学生中各选1人,有7×9种不同的选法;从一、四班学生中各选1人,有7×10种不同的选法;从二、三班学生中各选1人,有8×9种不同的选法;从二、 四班学生中各选1人,有8×10种不同的选法;从三、四班学生中各选1人,有9×10种不同的选法,所以共有不同的选法N=7×8+7×9+7×10+8×9+8×10+9×10=431种.
[方法总结]对于复杂问题,不能只用分类加法计数原理或分步乘法计数原理解决时,可以综合应用两个原理,可以先分类,在某一类中再分步,也可先分步,在某一步中再分类.
2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册
6.1分类加法计数原理与分步乘法计数原理课件
一、学习目标(1分钟)
学习两种基本计数原理
1、分类加法计数原理概念理解、应用理解
2、分步乘法计数原理概念理解、应用理解
二、问题导学(3分钟)
2022年3月4日政协十三届五次会议在北京人民大会堂举行,某政协委员3月2日要从湖北前往北京参加会议.他有两类快捷途径可供选择:一是乘飞机,二是乘坐动车组.假如这天飞机有3个航班可乘,动车组有4个班次可乘.
问:此委员这一天从湖北到北京共有多少种快捷途径可选?
例1.在模拟填写高考志愿表时,一名高中毕业生了解到A,B两所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学
B大学
生物学
化学
医学
物理学
工程学
数学
会计学
信息技术学
法学
如果他只能选一个专业,那么他共有多少种选择呢
三、点拨精讲(28分钟)
[分析] 由于这名同学在A,B两所大学中只能选择一所,而且只能选择一个专业,又由于两所大学没有共同的强项专业,因此符合分类加法计数原理的条件.
[解析] 这名同学可以选择A,B两所大学的一所,在A大学中有5种专业选择方法,在B大学中有4种专业选择方法,又由于没有一个强项专业是两所大学共有的,因此根据分类加法计数原理,这名同学可能的专业选择共有5+4=9(种).
[方法总结] 使用分类加法计数原理时,要根据问题的特点确定一个分类的标准.
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法.
分类加法计数原理
推广 完成一件事,有n类不同方案.在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,则完成这件事共有 N= m1+ m2+ ……+ mn种不同的方法.
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法.
分类加法计数原理
2.分类标准清晰,不重不漏;
1.各方法能独立的完成这件事;
3.可推广到n类.
变式:某班有男生26人,女生24人,从中选一位同学为数学课代表,则不同选法的种数是( )
A.50 B.26
C.24 D.616
[答案] A
[解析] 选一位同学或者选男生,或者选女生,用加法原理完成.
三、点拨精讲(28分钟)
例2:设某班有男生30名,女生24名.现要从中选出男、女生各
一名代表班级参加比赛,共有多少种不同的选法?
[解析] 第一步,从30名男生中选出1人,有30种不同的选法;
第二步,从24名女生中选出1人,有24种不同的选法.
根据分步乘法计数原理,共有30×24=720种不同的选法.
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法.
分步乘法计数原理
推广 完成一件事,需要分成n个步骤.做第1步有有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,则完成这件事共有 N= m1× m2× ……× mn种不同的方法.
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法.
分步乘法计数原理
1.各步相互依存, 每步都完成才算完成此事;
2.分步标准清晰 ;
3.可推广到n步.
1、4名同学去争夺3项冠军,不允许并列,共有多少种不同的情况?
[错解] 错解1:第一步,第1位同学去夺这3项冠军,有可能1项都不夺或夺1项、2项、3项,因此有4种不同的情况;
第二步,第2位同学去夺这3项冠军也有4种不同的情况;
第二步,第2位同学去夺这3项冠军也有4种不同的情况;
同理第3位、第4位同学也各有4种不同的情况.
由分步乘法计数原理,共有4×4×4×4=44=256种不同的情况.
易错疑难辨析
错解2:第一步,第1位同学去争冠军,有3种不同的情况;
第二步,第2位同学去争冠军,也有3种不同的情况;
同理第3位、第4位同学也各有3种不同的情况.
由分步乘法计算原理,共有3×3×3×3=34=81种不同的情况.
[辨析] 完成夺取冠军这件事,即每项冠军都有人夺取.错解1中可能有4位同学都不得冠军以及1项冠军不止1人获得这种情况,与题意不符;错解2中可能有1项冠军不止1人获得这种情况,也不符合题意.
[正解] 可分三步完成,第一项冠军被4名同学争夺,一定是其中1名而且只能是其中一名同学获得,共有4种不同的情况;同理其余2项冠军分被4名同学中的1名获得,各有4种不同的情况.由分步乘法计算原理,共有4×4×4=43=64种不同的夺得冠军的情况.
分类加法计数原理 分步乘法计数原理
相同点
不同点
注意点
用来计算“完成一件事”的方法种数
每类方案中的每一种方法都能______ 完成这件事
每步_________才算完成这件事情
(每步中的每一种方法不能独立完成这件事)
类类相加
步步相乘
类类独立
步步相依
独立
依次完成
不重不漏
步骤完整
分类完成
分步完成
四、课堂小结(1分钟)
五、当堂检测(12分钟)
练1:现有高一四个班学生34个,其中一、二、三、四班各7人、8人、9人、10人,他们自愿组成数学课外小组.
(1)选其中一人为负责人,有多少种不同的选法?
(2)每班选一名组长,有多少种不同的选法?
(3)推选二人作中心发言,这二人需来自不同的班级,有多少种不同的选法?
[分析] (1)是从四个班的34人中选一人,应分类求解,
(2)是从各班中选一人,共选4人,应分步求解,
(3)是先根据不同班级分类,再分步从两个班级中各选1人.
[解析] (1)分四类,第一类,从一班学生中选1人,有7种选法;第二类,从二班学生中选1人,有8种选法;第三类,从三班学生中选1人,有9种选法;第四类,从四班学生中选1人,有10种选法,所以,共有不同的选法N=7+8+9+10=34种.
(2)分四步,第一、二、三、四步分别从一、二、三、四班学生中选一人任组长,所以共有不同的选法N=7×8×9×10=5 040种.
(3)分六类,每类又分两步;从一班、二班学生中各选1人,有7×8种不同的选法;从一、三班学生中各选1人,有7×9种不同的选法;从一、四班学生中各选1人,有7×10种不同的选法;从二、三班学生中各选1人,有8×9种不同的选法;从二、 四班学生中各选1人,有8×10种不同的选法;从三、四班学生中各选1人,有9×10种不同的选法,所以共有不同的选法N=7×8+7×9+7×10+8×9+8×10+9×10=431种.
[方法总结]对于复杂问题,不能只用分类加法计数原理或分步乘法计数原理解决时,可以综合应用两个原理,可以先分类,在某一类中再分步,也可先分步,在某一步中再分类.
