人教版七年级数学下册 5.3.1平行线的性质 课件(共19张PPT)
文档属性
| 名称 | 人教版七年级数学下册 5.3.1平行线的性质 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 135.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 21:11:37 | ||
图片预览




文档简介
(共19张PPT)
第五章 相交线与平行线
5.3.1 平行线的性 质
5.3 平行线的性质
复习导入
1.到目前为止,判定两直线平行的方法有哪些?
(1)定义法
(2)平行公理的推论:若a//b,b//c,则a//c.
(3)判定方法1:同位角相等,两直线平行.
(4)判定方法2:内错角相等,两直线平行.
(5)判定方法3:同旁内角互补,两直线平行.
1.自学教材第第18-19页,并注意动手实践。
2.尝试完成20页课后练习。
自学指导
学习新知
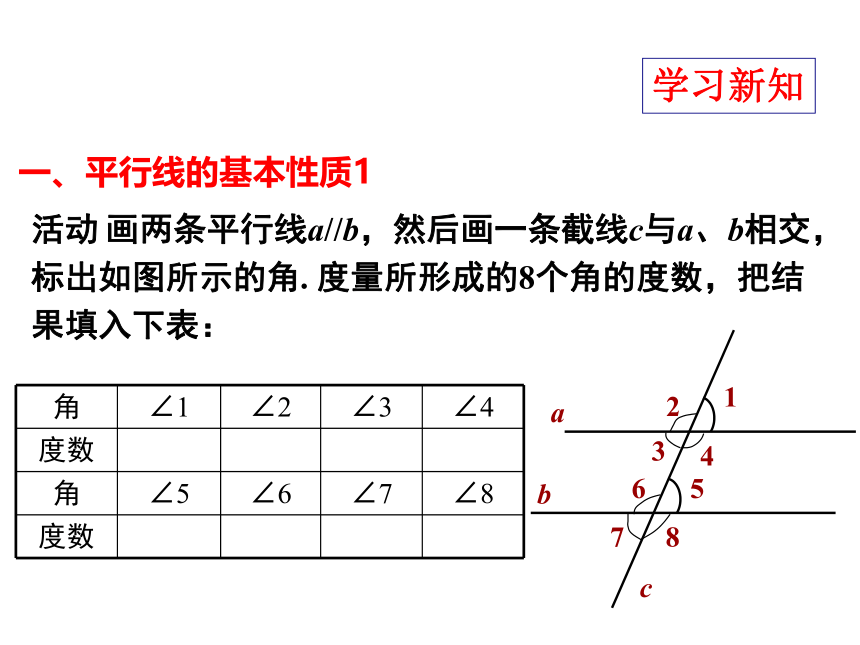
活动 画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
b
1
2
a
c
5
6
7
8
3
4
一、平行线的基本性质1
a
b
c
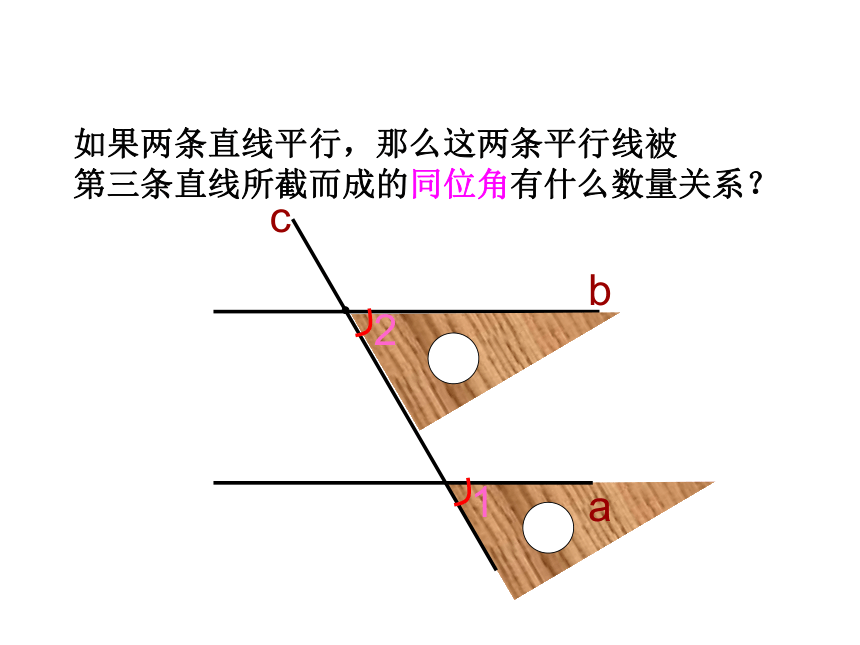
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
2
1
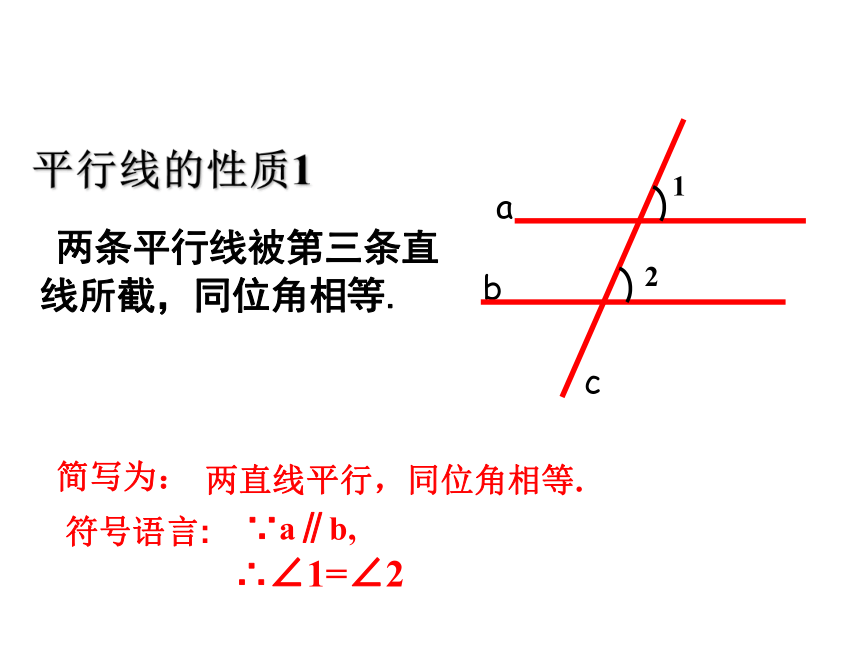
两直线平行,同位角相等.
平行线的性质1
两条平行线被第三条直线所截,同位角相等.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
∴∠1=∠2
思考:在上一节中,我们利用“同位角相等,两直线平行线”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等, 能否得到内错角之间的数量关系?
思考:类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补)
∵a∥b(已知)
应用格式:
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
完成平行线的性质表格
a
b
1
2
3
4
a
b
1
2
3
4
a
b
1
2
3
4
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3
= 180°
例1 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:因为梯形上、下底互相平行,所以
∠A与∠D互补, ∠B与∠C互补.
所以梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
2.如图,在汶川大地震当中,一辆抗震救灾汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么?
完成教材20页练习题,
请到前面展示一下!
学生展示
课堂提升
1.如图,由AB∥CE可得到结论是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
C
1
2
3
A
E
B
C
D
2.如图 AB ∥ CD ∥ EF, ∠ BAC+ ∠ ACE+ ∠ CEF=( )
A.180 °
D.540 °
C.360 °
B.270 °
C
A
B
E
D
F
课堂提升
3.如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度吗,为什么?
(2)从∠1=110o可以知道 ∠3是多少度吗,为什么?
(3)从 ∠1=110o可以知道∠4 是多少度吗,为什么?
2
3
E
1
4
A
B
D
C
解:(1)∠2=110o
∵两直线平行,内错角相等;
(2)∠3=110o
∵两直线平行, 同位角相等;
(3)∠4=70o
∵两直线平行,同旁内角互补.
解: ∵ AB∥DE( )
∴∠A=_______
( )
∵AC∥DF( )
∴∠D=______ ( )
∴∠A=∠D ( )
4.有这样一道题:如图1,若AB∥DE , AC∥DF,试
说明∠A=∠D.请补全下面的解答过程,括号内填写依据.
P
F
C
E
B
A
D
图1
已知
∠CPE
两直线平行,同位角相等
已知
∠CPE
两直线平行,同位角相等
等量代换
课堂小结
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
学习贵在坚持
第五章 相交线与平行线
5.3.1 平行线的性 质
5.3 平行线的性质
复习导入
1.到目前为止,判定两直线平行的方法有哪些?
(1)定义法
(2)平行公理的推论:若a//b,b//c,则a//c.
(3)判定方法1:同位角相等,两直线平行.
(4)判定方法2:内错角相等,两直线平行.
(5)判定方法3:同旁内角互补,两直线平行.
1.自学教材第第18-19页,并注意动手实践。
2.尝试完成20页课后练习。
自学指导
学习新知
活动 画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
b
1
2
a
c
5
6
7
8
3
4
一、平行线的基本性质1
a
b
c
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
2
1
两直线平行,同位角相等.
平行线的性质1
两条平行线被第三条直线所截,同位角相等.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
∴∠1=∠2
思考:在上一节中,我们利用“同位角相等,两直线平行线”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等, 能否得到内错角之间的数量关系?
思考:类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补)
∵a∥b(已知)
应用格式:
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
完成平行线的性质表格
a
b
1
2
3
4
a
b
1
2
3
4
a
b
1
2
3
4
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3
= 180°
例1 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:因为梯形上、下底互相平行,所以
∠A与∠D互补, ∠B与∠C互补.
所以梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
2.如图,在汶川大地震当中,一辆抗震救灾汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么?
完成教材20页练习题,
请到前面展示一下!
学生展示
课堂提升
1.如图,由AB∥CE可得到结论是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
C
1
2
3
A
E
B
C
D
2.如图 AB ∥ CD ∥ EF, ∠ BAC+ ∠ ACE+ ∠ CEF=( )
A.180 °
D.540 °
C.360 °
B.270 °
C
A
B
E
D
F
课堂提升
3.如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度吗,为什么?
(2)从∠1=110o可以知道 ∠3是多少度吗,为什么?
(3)从 ∠1=110o可以知道∠4 是多少度吗,为什么?
2
3
E
1
4
A
B
D
C
解:(1)∠2=110o
∵两直线平行,内错角相等;
(2)∠3=110o
∵两直线平行, 同位角相等;
(3)∠4=70o
∵两直线平行,同旁内角互补.
解: ∵ AB∥DE( )
∴∠A=_______
( )
∵AC∥DF( )
∴∠D=______ ( )
∴∠A=∠D ( )
4.有这样一道题:如图1,若AB∥DE , AC∥DF,试
说明∠A=∠D.请补全下面的解答过程,括号内填写依据.
P
F
C
E
B
A
D
图1
已知
∠CPE
两直线平行,同位角相等
已知
∠CPE
两直线平行,同位角相等
等量代换
课堂小结
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
学习贵在坚持
