6.3实数 课件(共17张PPT)
文档属性
| 名称 | 6.3实数 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1008.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 12:01:11 | ||
图片预览






文档简介
(共17张PPT)
6.3 实数
第六章 实数
七年级数学下册同步(人教版)
学习目标
1、理解无理数和实数的概念。
2、对实数进行分类,判断一个数是有理数还是无理数。
3、理解实数和数轴上的点一一对应。
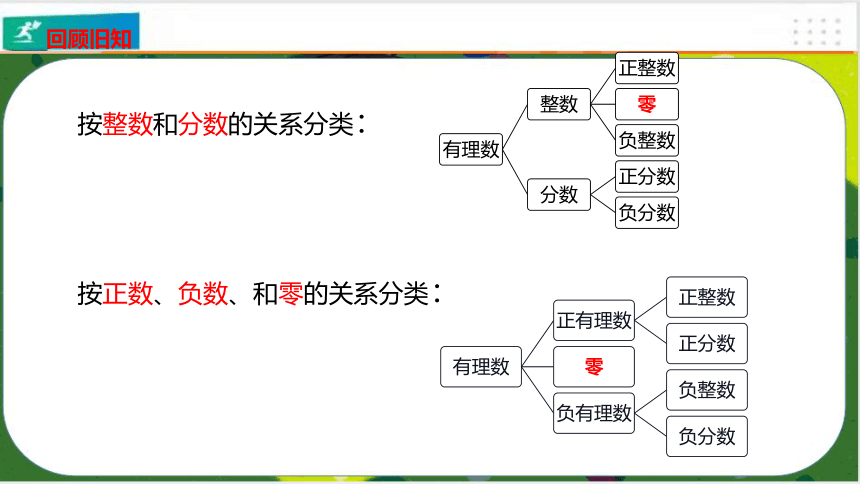
按整数和分数的关系分类:
按正数、负数、和零的关系分类:
回顾旧知
是有理数吗?
探究新知
使用计算器,把下列数化成小数的形式:
无限不循环小数叫做无理数;
探究新知
无理数
无限不循环的小数叫做无理数。
结合本章所学知识,举例:
无理数的分类:
结合无理数概念,举例:
.333133343…,3.3456789…,…
1.圆周率π及一些含π的数是无理数。
2.含根号的数不一定是无理数。(例: 等)
【注意】
总结归纳
1.判断下列说法是否正确;
(1)无限小数都是无理数.( )
(2)无理数都是无限小数.( )
(3)带根号的数都是无理数.( )
对
错
错
巩固提高
有理数集合
无理数集合
2.把下列各数分别填在相应的集合中;
巩固提高
有理数和无理数统称为实数。
有限小数或无限循环小数
无限不循环小数
总结归纳
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点来表示呢?如果可以你能在数轴上找到表示 这样的无理数的点吗?
是有理数吗?
是无理数
合作探究
数轴上的点可以表示有理数,那它可以表示无理数吗,你能在数轴上画出表示的点吗?
0
1
2
3
4
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数。
合作探究
负实数
正实数
数实
正有理数
负有理数
0
正无理数
负无理数
性格开朗的大孩子
性格内向的小孩子
0
正实数
负实数
课堂小结
1.在实数中,无理数的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【详解】
解:在实数中,无理数有,这2个,
故选:B.
当堂检测
2.下列说法不正确的是( )
A.如果数轴上的点表示的数不是有理数,那么就一定是无理数
B.大小介于两个有理数之间的无理数有无数个
C.-1的立方是-1,立方根也是-1
D.两个实数,较大者的平方也较大
【详解】
∵数轴上的点和实数一一对应,故选项A正确;
无理数是无限不循环小数,故选项B正确;
-1的立方是-1,立方根也是-1,故选项C正确;
实数包括正数和负数,故选项D错误.故选D.
当堂检测
3.如图,数轴上A,B,C,D四点中,与-对应的点距离最近的是( )
A.点A B.点B C.点C D.点D
【答案】B
【详解】
解:∵<<,即1<<2,
∴﹣2<<﹣1,
∴由数轴知,与对应的点距离最近的是点B,
故选:B.
当堂检测
https://www.21cnjy.com/help/help_extract.php
6.3 实数
第六章 实数
七年级数学下册同步(人教版)
学习目标
1、理解无理数和实数的概念。
2、对实数进行分类,判断一个数是有理数还是无理数。
3、理解实数和数轴上的点一一对应。
按整数和分数的关系分类:
按正数、负数、和零的关系分类:
回顾旧知
是有理数吗?
探究新知
使用计算器,把下列数化成小数的形式:
无限不循环小数叫做无理数;
探究新知
无理数
无限不循环的小数叫做无理数。
结合本章所学知识,举例:
无理数的分类:
结合无理数概念,举例:
.333133343…,3.3456789…,…
1.圆周率π及一些含π的数是无理数。
2.含根号的数不一定是无理数。(例: 等)
【注意】
总结归纳
1.判断下列说法是否正确;
(1)无限小数都是无理数.( )
(2)无理数都是无限小数.( )
(3)带根号的数都是无理数.( )
对
错
错
巩固提高
有理数集合
无理数集合
2.把下列各数分别填在相应的集合中;
巩固提高
有理数和无理数统称为实数。
有限小数或无限循环小数
无限不循环小数
总结归纳
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点来表示呢?如果可以你能在数轴上找到表示 这样的无理数的点吗?
是有理数吗?
是无理数
合作探究
数轴上的点可以表示有理数,那它可以表示无理数吗,你能在数轴上画出表示的点吗?
0
1
2
3
4
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数。
合作探究
负实数
正实数
数实
正有理数
负有理数
0
正无理数
负无理数
性格开朗的大孩子
性格内向的小孩子
0
正实数
负实数
课堂小结
1.在实数中,无理数的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【详解】
解:在实数中,无理数有,这2个,
故选:B.
当堂检测
2.下列说法不正确的是( )
A.如果数轴上的点表示的数不是有理数,那么就一定是无理数
B.大小介于两个有理数之间的无理数有无数个
C.-1的立方是-1,立方根也是-1
D.两个实数,较大者的平方也较大
【详解】
∵数轴上的点和实数一一对应,故选项A正确;
无理数是无限不循环小数,故选项B正确;
-1的立方是-1,立方根也是-1,故选项C正确;
实数包括正数和负数,故选项D错误.故选D.
当堂检测
3.如图,数轴上A,B,C,D四点中,与-对应的点距离最近的是( )
A.点A B.点B C.点C D.点D
【答案】B
【详解】
解:∵<<,即1<<2,
∴﹣2<<﹣1,
∴由数轴知,与对应的点距离最近的是点B,
故选:B.
当堂检测
https://www.21cnjy.com/help/help_extract.php
