6.2立方根 课件(共21张PPT)
图片预览








文档简介
(共21张PPT)
6.2 立方根
第六章 实数
七年级数学下册同步(人教版)
学习目标
1、理解立方根的概念,会用符号表示一个数的立方根。(重点)
2、了解开立方与立方根互为逆运算。
3、会求一个数的立方根。(难点)
问
题
要制作一种容积为27m3的正方体形状的包装箱,这种包装箱的棱长应该是多?
情境导入
设这种包装箱的棱长为x m,则
x3 = 27
这就是要求一个数,使它的立方等于27.
因为33 = 27,所以x = 3.
因此这种包装箱的棱长为3 m.
探究新知
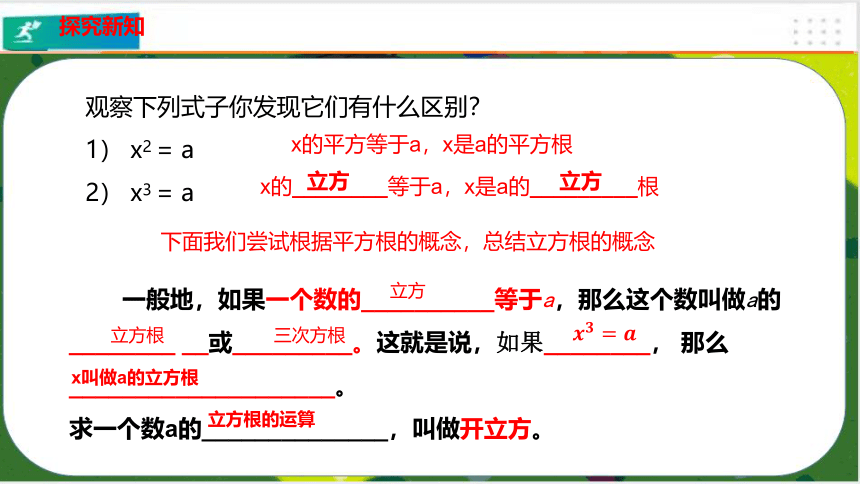
观察下列式子你发现它们有什么区别?
1) x2 = a
2) x3 = a
x的平方等于a,x是a的平方根
x的________等于a,x是a的_________根
立方
立方
下面我们尝试根据平方根的概念,总结立方根的概念
一般地,如果一个数的__________等于a,那么这个数叫做a的________ __或_________。这就是说,如果________, 那么____________________。
求一个数a的______________,叫做开立方。
立方
三次方根
立方根
x叫做a的立方根
立方根的运算
探究新知
类似于平方根,一个数a的立方根,用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
表示8的立方根, = 2
表示﹣8的立方根, = ﹣2
中的根指数3不能省略.
总结归纳
求下列各式的值
1) 2)- 3) 4) -
解:1)
2)- = -=-2
3) = = -3
4) - = -= -3
观察结果你发现了什么?
合作探究
一般地,
=
1.求下列各式的值.
(1)
(2)
(3)
(4)
10
– 0.1
– 1
尝试练习
2.比较3,4, 的大小.
解:33 = 27,43 = 64
因为27 < 50 < 64
所以3 < < 4
尝试练习
用计算器计算一个数的立方根
实际上,有很多有理数的立方根是无限不循环小数,例如 , 等都是无限不循环小数.我们可以用有理数近似地表示它们.
一些计算器设有 键,用它可以求出一个数的立方根(或其近似值).
合作探究
有些计算器需要用第二功能键求一个数的立方根. 例如用这种计算器求 ,可以依次按键 1845 ,显示
12.264 940 81.
2nd F
=
合作探究
在计算器上按键: ,显示的结果为( )
A.-5 B. C. D.
【答案】A
【详解】
解:在计算器上按键,
是在计算,结果为-5,
故选A.
合作探究
利用计算器求下列各式的值.
(1)
(2)
(2)
12
25
±13
如果x3 = a,那么x叫做a的立方根
性质
定义
正数的立方根是正数,
负数的立方根是负数;
0的立方根是0.
被开方数的小数点向左或向右移动3n位时立方根的小数点就相应的向左或向右移动n位(n为正整数).
用计算器计算
立方根
课堂小结
1.下列各式中正确的是( )
A. B.
C. D.
【答案】A
【详解】
解:A、,故A选项符合题意;
B、,故B选项不符合题意;
C、,故C选项不符合题意;
D、,故D选项不符合题意;
故答案为:A.
当堂检测
A
2.下列运算中:①;②;③;④,错误的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【详解】
①,故该项错误;②无意义,故该项错误;
③,故该项错误;④,故该项错误.
共4个错误的,故选:D.
D
当堂检测
3.若a,b(a≠b)是64的平方根,则的值为( )
A.8 B.-8 C.4 D.0
【答案】D
【详解】
∵a,b(a≠b)是64的平方根,
∴a=-8,b=8或a=8,b=-8,
当a=-8,b=8时,=-2+2=0;
当a=8,b=-8时,=2-2=0;
故选D.
D
当堂检测
4.求下列各式的值.
(1)
(2)
(3)
(4)
= – 0.3
=
=
=
=
=
当堂检测
若 =2, =4,求 的值.
解:∵ =2, =4.
∴x = 23,y2 = 16,
∴x = 8,y = ±4.
∴x + 2y = 8 + 2×4 = 16 或 x + 2y = 8 – 2×4 = 0.
∴ = = 4 或 = = 0.
应用拓展
https://www.21cnjy.com/help/help_extract.php
6.2 立方根
第六章 实数
七年级数学下册同步(人教版)
学习目标
1、理解立方根的概念,会用符号表示一个数的立方根。(重点)
2、了解开立方与立方根互为逆运算。
3、会求一个数的立方根。(难点)
问
题
要制作一种容积为27m3的正方体形状的包装箱,这种包装箱的棱长应该是多?
情境导入
设这种包装箱的棱长为x m,则
x3 = 27
这就是要求一个数,使它的立方等于27.
因为33 = 27,所以x = 3.
因此这种包装箱的棱长为3 m.
探究新知
观察下列式子你发现它们有什么区别?
1) x2 = a
2) x3 = a
x的平方等于a,x是a的平方根
x的________等于a,x是a的_________根
立方
立方
下面我们尝试根据平方根的概念,总结立方根的概念
一般地,如果一个数的__________等于a,那么这个数叫做a的________ __或_________。这就是说,如果________, 那么____________________。
求一个数a的______________,叫做开立方。
立方
三次方根
立方根
x叫做a的立方根
立方根的运算
探究新知
类似于平方根,一个数a的立方根,用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
表示8的立方根, = 2
表示﹣8的立方根, = ﹣2
中的根指数3不能省略.
总结归纳
求下列各式的值
1) 2)- 3) 4) -
解:1)
2)- = -=-2
3) = = -3
4) - = -= -3
观察结果你发现了什么?
合作探究
一般地,
=
1.求下列各式的值.
(1)
(2)
(3)
(4)
10
– 0.1
– 1
尝试练习
2.比较3,4, 的大小.
解:33 = 27,43 = 64
因为27 < 50 < 64
所以3 < < 4
尝试练习
用计算器计算一个数的立方根
实际上,有很多有理数的立方根是无限不循环小数,例如 , 等都是无限不循环小数.我们可以用有理数近似地表示它们.
一些计算器设有 键,用它可以求出一个数的立方根(或其近似值).
合作探究
有些计算器需要用第二功能键求一个数的立方根. 例如用这种计算器求 ,可以依次按键 1845 ,显示
12.264 940 81.
2nd F
=
合作探究
在计算器上按键: ,显示的结果为( )
A.-5 B. C. D.
【答案】A
【详解】
解:在计算器上按键,
是在计算,结果为-5,
故选A.
合作探究
利用计算器求下列各式的值.
(1)
(2)
(2)
12
25
±13
如果x3 = a,那么x叫做a的立方根
性质
定义
正数的立方根是正数,
负数的立方根是负数;
0的立方根是0.
被开方数的小数点向左或向右移动3n位时立方根的小数点就相应的向左或向右移动n位(n为正整数).
用计算器计算
立方根
课堂小结
1.下列各式中正确的是( )
A. B.
C. D.
【答案】A
【详解】
解:A、,故A选项符合题意;
B、,故B选项不符合题意;
C、,故C选项不符合题意;
D、,故D选项不符合题意;
故答案为:A.
当堂检测
A
2.下列运算中:①;②;③;④,错误的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【详解】
①,故该项错误;②无意义,故该项错误;
③,故该项错误;④,故该项错误.
共4个错误的,故选:D.
D
当堂检测
3.若a,b(a≠b)是64的平方根,则的值为( )
A.8 B.-8 C.4 D.0
【答案】D
【详解】
∵a,b(a≠b)是64的平方根,
∴a=-8,b=8或a=8,b=-8,
当a=-8,b=8时,=-2+2=0;
当a=8,b=-8时,=2-2=0;
故选D.
D
当堂检测
4.求下列各式的值.
(1)
(2)
(3)
(4)
= – 0.3
=
=
=
=
=
当堂检测
若 =2, =4,求 的值.
解:∵ =2, =4.
∴x = 23,y2 = 16,
∴x = 8,y = ±4.
∴x + 2y = 8 + 2×4 = 16 或 x + 2y = 8 – 2×4 = 0.
∴ = = 4 或 = = 0.
应用拓展
https://www.21cnjy.com/help/help_extract.php
