6.1.1 算术平方根 课件(共15张PPT)
文档属性
| 名称 | 6.1.1 算术平方根 课件(共15张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 856.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
6.1.1 算术平方根
第六章 实数
七年级数学下册同步(人教版)
学习目标
1.理解算术平方根的概念.
2.根据算术平方根的概念求一个数的算术平方根.(重点)
3.理解平方根与算术平方根的区别和联系.(难点)
1.什么叫平方根?
2.平方根的性质有哪些?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果 ,那么x 叫做a的平方根.
(1)一个正数有两个平方根,它们互为相反数;
(2)0只有两平方根,是0本身;
(3)负数没有平方根.
回顾旧知
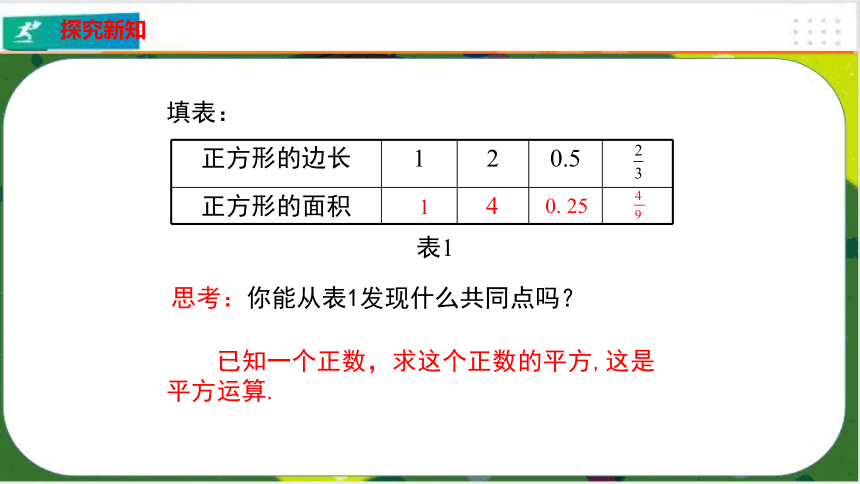
已知一个正数,求这个正数的平方,这是平方运算.
正方形的边长 1 2 0.5
正方形的面积
1
填表:
表1
思考:你能从表1发现什么共同点吗?
4
0. 25
探究新知
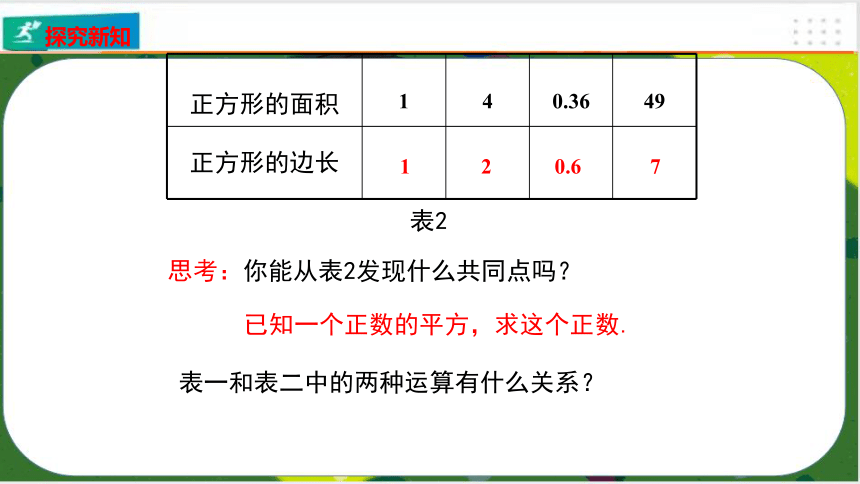
正方形的面积 1 4 0.36
49
正方形的边长
已知一个正数的平方,求这个正数.
表2
表一和表二中的两种运算有什么关系?
1
2
0.6
7
思考:你能从表2发现什么共同点吗?
探究新知
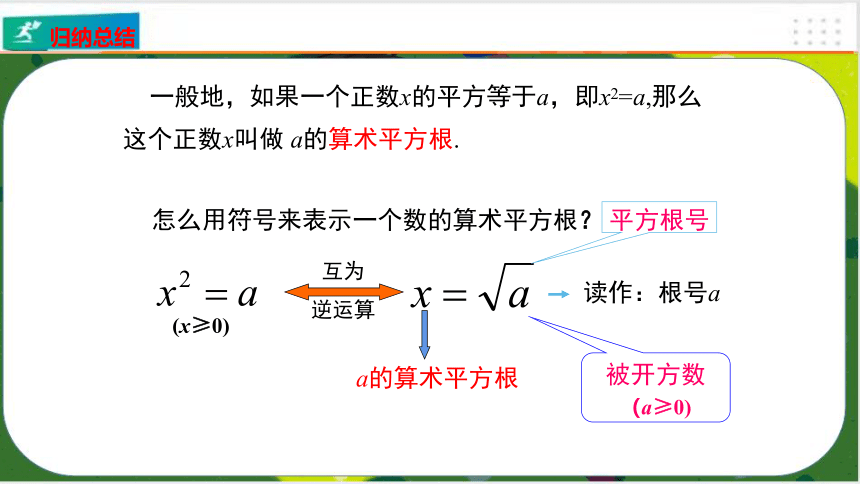
a的算术平方根
互为
逆运算
平方根号
被开方数
读作:根号a
(a≥0)
怎么用符号来表示一个数的算术平方根?
(x≥0)
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做 a的算术平方根.
归纳总结
1.若一个数的算术平方根是 ,那么这个数是 ;
2. 的算术平方根是 ;
3. 的算术平方根是 ;
4.若 ,则 .
7
16
尝试练习
1.若 的算术平方根是3,则a =________.
81
2.下列命题中,正确的个数有( )
①1的平方根是1 ;②1是1的算术平方根;
③( 1)2的平方根是 1;④0的算术平方根是它本身
A.1个 B.2个 C.3个 D.4个
B
3.已知x,y满足 ,则xy的值是( )
A.4 B.-4 C. D.
B
尝试练习
例1 分别求下列各数的算术平方根:
(1)100, (2) , (3) .
解:(1)由于102=100,
因此 ;
(2)由于 2= ,
因此 ;
(3)由于0.72=0.49,
因此 .
不难看出:被开方数越大,对应的算术平方根也越大.这个结论对所有正数都成立.
巩固提高
例2 计算:
(1) ; (2) .
解:(1)原式=7+3-1=9;
(2)原式=2+3-4=1.
巩固提高
1、这节课主要学习了算术平方根的概念和表示方法,知道了求一个正数的算术平方根与求一个正数的二次幂正好是互逆的过程,因此,求正数的算术平方根实际上可以转化为求一个数的二次幂运算. 只不过,只有正数和0才有算术平方根.
2、求一个正数的算术平方根运算和开平方求一个正数的二次幂运算互为逆运算..
课堂小结
填空:(看谁算得又对又快)
(1) 一个数的算术平方根是3,则这个数是 .
(2) 一个自然数的算术平方根为a,则这个自然数
是___;和这个自然数相邻的下一个自然数是
.
(3) 的算术平方根为 .
(4) 2的算术平方根为____.
3
9
a2
a2+1
当堂检测
如果将一个长方形ABCD折叠,得到一个面积为144cm2的正方形ABFE,已知正方形ABFE的面积等于长方形CDEF面积的2倍,求长方形ABCD的长和宽.
解:
设正方形ABFE的边长为a,
有 ,所以 ,
所以 .
又因为 ,设 ,
所以 , .
所以 (cm).
所以长方形的长为18cm,宽为12cm.
应用拓展
https://www.21cnjy.com/help/help_extract.php
6.1.1 算术平方根
第六章 实数
七年级数学下册同步(人教版)
学习目标
1.理解算术平方根的概念.
2.根据算术平方根的概念求一个数的算术平方根.(重点)
3.理解平方根与算术平方根的区别和联系.(难点)
1.什么叫平方根?
2.平方根的性质有哪些?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果 ,那么x 叫做a的平方根.
(1)一个正数有两个平方根,它们互为相反数;
(2)0只有两平方根,是0本身;
(3)负数没有平方根.
回顾旧知
已知一个正数,求这个正数的平方,这是平方运算.
正方形的边长 1 2 0.5
正方形的面积
1
填表:
表1
思考:你能从表1发现什么共同点吗?
4
0. 25
探究新知
正方形的面积 1 4 0.36
49
正方形的边长
已知一个正数的平方,求这个正数.
表2
表一和表二中的两种运算有什么关系?
1
2
0.6
7
思考:你能从表2发现什么共同点吗?
探究新知
a的算术平方根
互为
逆运算
平方根号
被开方数
读作:根号a
(a≥0)
怎么用符号来表示一个数的算术平方根?
(x≥0)
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做 a的算术平方根.
归纳总结
1.若一个数的算术平方根是 ,那么这个数是 ;
2. 的算术平方根是 ;
3. 的算术平方根是 ;
4.若 ,则 .
7
16
尝试练习
1.若 的算术平方根是3,则a =________.
81
2.下列命题中,正确的个数有( )
①1的平方根是1 ;②1是1的算术平方根;
③( 1)2的平方根是 1;④0的算术平方根是它本身
A.1个 B.2个 C.3个 D.4个
B
3.已知x,y满足 ,则xy的值是( )
A.4 B.-4 C. D.
B
尝试练习
例1 分别求下列各数的算术平方根:
(1)100, (2) , (3) .
解:(1)由于102=100,
因此 ;
(2)由于 2= ,
因此 ;
(3)由于0.72=0.49,
因此 .
不难看出:被开方数越大,对应的算术平方根也越大.这个结论对所有正数都成立.
巩固提高
例2 计算:
(1) ; (2) .
解:(1)原式=7+3-1=9;
(2)原式=2+3-4=1.
巩固提高
1、这节课主要学习了算术平方根的概念和表示方法,知道了求一个正数的算术平方根与求一个正数的二次幂正好是互逆的过程,因此,求正数的算术平方根实际上可以转化为求一个数的二次幂运算. 只不过,只有正数和0才有算术平方根.
2、求一个正数的算术平方根运算和开平方求一个正数的二次幂运算互为逆运算..
课堂小结
填空:(看谁算得又对又快)
(1) 一个数的算术平方根是3,则这个数是 .
(2) 一个自然数的算术平方根为a,则这个自然数
是___;和这个自然数相邻的下一个自然数是
.
(3) 的算术平方根为 .
(4) 2的算术平方根为____.
3
9
a2
a2+1
当堂检测
如果将一个长方形ABCD折叠,得到一个面积为144cm2的正方形ABFE,已知正方形ABFE的面积等于长方形CDEF面积的2倍,求长方形ABCD的长和宽.
解:
设正方形ABFE的边长为a,
有 ,所以 ,
所以 .
又因为 ,设 ,
所以 , .
所以 (cm).
所以长方形的长为18cm,宽为12cm.
应用拓展
https://www.21cnjy.com/help/help_extract.php
