3.3.1用图象表示的变量间关系(1) 课件(共28张PPT)
文档属性
| 名称 | 3.3.1用图象表示的变量间关系(1) 课件(共28张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 13:32:49 | ||
图片预览




文档简介
(共27张PPT)
3.3.1用图象表示的变量间关系(1)
第三章
变量之间的关系
七年级数学下册同步(北师大版)
学习目标
1、了解两个变量之间的对应关系,初步形成函数的思想.
2、结合具体情境理解图象上的点所表示的意义.
3、发展从图象中获得信息的能力及有条理地进行语言表达的能力.
4、理解用数学的方法描述变量之间的关系,感受数学的价值.
导入新课
对于两个变量之间的关系,我们已经分别学习了
________和__________两种表示方法.
列表法
关系式法
列表法:具体而直接,但是数据有限
关系式法:严谨而抽象,具有一般性
导入新课
同学们见过股市走势图吗?生活中还有那些类似现象?
你能看懂这些图象吗?
本节课我们就来学习:用图象来表示一些量与量之间的关系.
讲授新课
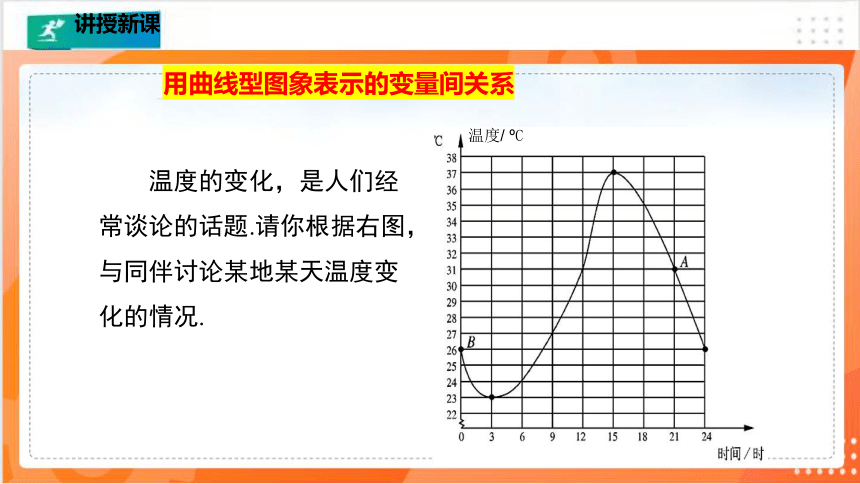
用曲线型图象表示的变量间关系
温度的变化,是人们经常谈论的话题.请你根据右图,与同伴讨论某地某天温度变化的情况.
温度/ C
讲授新课
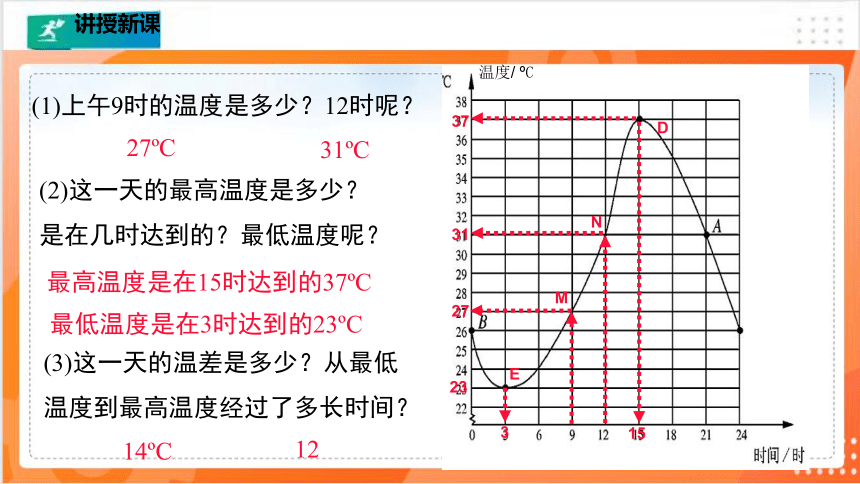
(1)上午9时的温度是多少?12时呢?
(2)这一天的最高温度是多少?
是在几时达到的?最低温度呢?
(3)这一天的温差是多少?从最低温度到最高温度经过了多长时间?
温度/ C
27
31
M
D
N
37
15
E
23
3
14 C
27 C
31 C
最高温度是在15时达到的37 C
最低温度是在3时达到的23 C
12
上图表示了温度随时间的变化而变化的情况,它是温度与时间之间关系的图象.图象是我们表示变量之间关系的又一种方法,它的特点是非常直观.
归纳总结
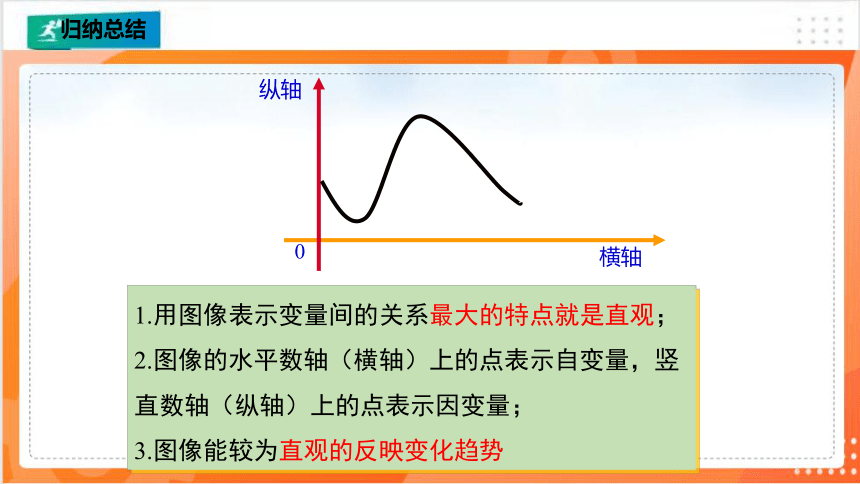
横轴
纵轴
0
1.用图像表示变量间的关系最大的特点就是直观;
2.图像的水平数轴(横轴)上的点表示自变量,竖直数轴(纵轴)上的点表示因变量;
3.图像能较为直观的反映变化趋势
归纳总结
议一议
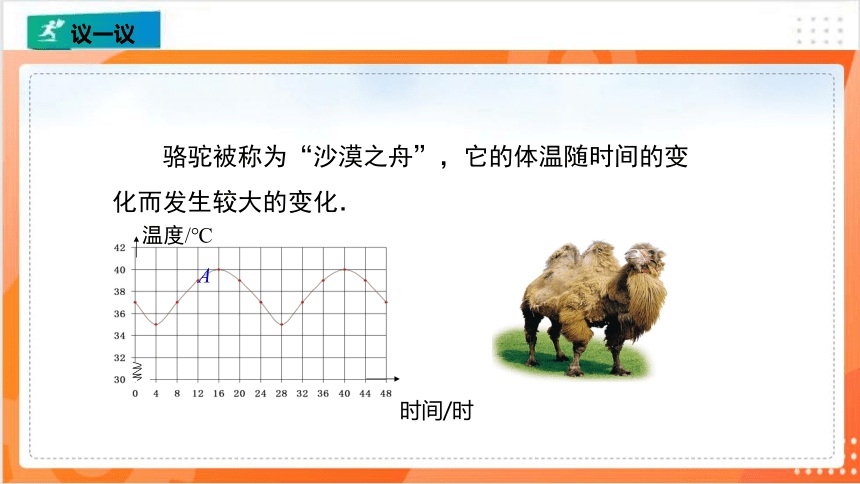
骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化.
A
温度/℃
时间/时
讲授新课
(1)一天中,骆驼的体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?
(2)从16时到24时,骆驼的体温下降了多少?
A
温度/℃
时间/时
体温的变化范围是35至40℃,
从4时最低到16时最高需要12小时
从16时的40℃到24时的37℃下降了3℃
讲授新课
A
温度/℃
时间/时
(3)在什么时间范围内骆驼的体温在上升?
在什么时间范围内骆驼的体温在下降?
(4)你能看出第二天8时骆驼的体温与第一天8时有什么关系吗? 其他时刻呢?
上升:4至16时和28至40时
下降:0至4时,16至28时和40至48时
体温一样
讲授新课
A
温度/℃
时间/时
(5)A点表示的是什么?还有几时的温度与A点所表示的温度相同?
A点表示12时的温度是39℃, 20时、36时及44时的温度与A点所表示的温度相同.
讲授新课
(6)你还知道哪些关于骆驼的趣事?与同伴进行交流.
骆驼非常适合,或者说适应在昼热夜寒、缺少水和绿色植物地上生活,例如非洲的撒哈拉大沙漠或中亚的戈壁滩.
骆驼吃各种植物,甚至包括其他动物碰都不碰的荆棘和含盐的灌木,为寻找食物,它们会长途跋渺.骆驼具有惊人的能力,可以在缺水的情况下行走很长的时间.
归纳总结
拓展:图象(或其局部)如果呈“/”(含“ ”“ ”等)状,
就说明因变量随着自变量的增加而增加.
图象(或其局部)如果呈“\”(含“ ”“ ”等)状,
就表示因变量随着自变量的增加而减少.
图象呈“ ”(含“∧”等)状,表示因变量先随着自变量的增加而增加,然后随着自变量的增加而减少.
图象呈“ ”(含“∨”等)状,表示因变量先随着自变量的增加而减少,然后随着自变量的增加而增加.
讲授新课
三种表示变量之间关系的方法和优缺点:
方法 优点 缺点
表格法 对于表中自变量的每一个值,可以不通过计算,直接把因变量的值找到,查询时很方便,于是一些数学用表应运而生 只能列出部分自变量与因变量的对应值,难以反映变量间变化的全貌,而且从表中看不出变量间的对应规律
关系式法 关系式简明扼要,规范准确 有些变量之间的关系很难或不能用关系式表示,求对应值也需要逐个计算,比较麻烦
图象法 形象直观,可以形象地反映出事物变图象/化的全过程、变化的趋势和某些性质图象是近似的、局部的,由观察图象确定的大或最小值等) 图象是近似的、局部的,由观察图象确定的因变量的值往往不够准确
当堂检测
1.在一次足球比赛中,守门员用脚踢出去的球的高度h随时间t的变化而变化,可以近似地表示h与t的关系的图象是( )
C
当堂检测
2.如图,图象记录了某地一月份某天的温度随时间变化的情况,请你仔细观察图象,根据图中提供的信息,判断不符合图象描述的说法是( )
A.20时的温度约为-1 ℃
B.温度是2 ℃的时刻是12时
C.最暖和的时刻是14时
D.在-3 ℃以下的时间约为8小时
B
当堂检测
3. 下列各情境分别可以用哪幅图来近似刻画 (1)凉水逐渐加热转化为水蒸气跑掉(水温与时间的关系);(2)匀速行驶的火车(速度与时间的关系);(3)运动员推出去的铅球(高度与时间的关系);(4)小明匀速从A地走到B地后逗留一段时间,然后按原速返回(小明距A地的距离与时间的关系).
当堂检测
A是 的图象,
B是 的图象,
C是 的图象,
D是 的图象.(填序号)
(4)
(2)
(1)
(3)
当堂检测
4. 如图所示的图象记录了某地一月份某天的气温随时间变化的情况,请你仔细观察图象回答下面的问题:20时的气温是 ℃;气温是0 ℃的时刻是 时;气温最高的时刻是 时.
-1
12和18
14
当堂检测
5. 如图表示某市2019年6月份某一天的气温随时间变化的情况,请回答下列问题:
(1)这天的最高气温是多少
(2)这天共有几个小时的气温在31 ℃以上
(3)这天在什么时间范围内气温在上升
(4)点A表示的意义是什么 还有几时的气
温与点A表示的气温相同
(5)请你预测,次日凌晨1点的气温大约是 ℃.
当堂检测
解:(1)36 ℃
(2)9个
(3)3~15时
(4)点A表示的意义是12时的气温是31℃;
21时的气温与点A表示的气温相同
(5)25
当堂检测
6.海水受日月的引力而产生潮汐现象,早晨海水上涨叫做潮,黄昏海水上涨叫做汐,合称潮汐.潮汐与人类的生活有着密切的联系.下面是某港口从 0时到12时的水深情况.
当堂检测
(1)大约什么时刻港口的水最深?深度约是多少?
(2)大约什么时刻港口的水最浅?深度约是多少?
(3)在什么时间范围内,港口水深在增加?
大约3时刻港口的水最深,深度约7. 5m
大约9时刻港口的水最浅,深度约是2.4m
0时到3时和9时到12时港口水深在增加
(4)在什么时间范围内,港口水深在减少?
3时到9时港口水深在减少.
当堂检测
(5) A,B 两点分别表示什么?还有几时水的深度与A 点所表示的深度相同?
A点表示6时港口的水深大约为5m,B 点表示12时港口的水深大约为4.3m;0时水的深度与A点所表示的深度相同.
(6) 说一说这个港口从 0 时 到 12 时 的水深是怎样变化的.
0时到3时水深在增加,3时到9时水深在减少,9时到12时水深又在增加.
课堂小结
其特点是直观
变量之间的关系
表格法
关系式法
图象法
从“数”的角度反映
变量之间的关系:
其特点是清楚
从“式”的角度反映
变量之间的关系:
其特点是简单明了
从“形”的角度反映
变量之间的关系:
3.3.1用图象表示的变量间关系(1)
第三章
变量之间的关系
七年级数学下册同步(北师大版)
学习目标
1、了解两个变量之间的对应关系,初步形成函数的思想.
2、结合具体情境理解图象上的点所表示的意义.
3、发展从图象中获得信息的能力及有条理地进行语言表达的能力.
4、理解用数学的方法描述变量之间的关系,感受数学的价值.
导入新课
对于两个变量之间的关系,我们已经分别学习了
________和__________两种表示方法.
列表法
关系式法
列表法:具体而直接,但是数据有限
关系式法:严谨而抽象,具有一般性
导入新课
同学们见过股市走势图吗?生活中还有那些类似现象?
你能看懂这些图象吗?
本节课我们就来学习:用图象来表示一些量与量之间的关系.
讲授新课
用曲线型图象表示的变量间关系
温度的变化,是人们经常谈论的话题.请你根据右图,与同伴讨论某地某天温度变化的情况.
温度/ C
讲授新课
(1)上午9时的温度是多少?12时呢?
(2)这一天的最高温度是多少?
是在几时达到的?最低温度呢?
(3)这一天的温差是多少?从最低温度到最高温度经过了多长时间?
温度/ C
27
31
M
D
N
37
15
E
23
3
14 C
27 C
31 C
最高温度是在15时达到的37 C
最低温度是在3时达到的23 C
12
上图表示了温度随时间的变化而变化的情况,它是温度与时间之间关系的图象.图象是我们表示变量之间关系的又一种方法,它的特点是非常直观.
归纳总结
横轴
纵轴
0
1.用图像表示变量间的关系最大的特点就是直观;
2.图像的水平数轴(横轴)上的点表示自变量,竖直数轴(纵轴)上的点表示因变量;
3.图像能较为直观的反映变化趋势
归纳总结
议一议
骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化.
A
温度/℃
时间/时
讲授新课
(1)一天中,骆驼的体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?
(2)从16时到24时,骆驼的体温下降了多少?
A
温度/℃
时间/时
体温的变化范围是35至40℃,
从4时最低到16时最高需要12小时
从16时的40℃到24时的37℃下降了3℃
讲授新课
A
温度/℃
时间/时
(3)在什么时间范围内骆驼的体温在上升?
在什么时间范围内骆驼的体温在下降?
(4)你能看出第二天8时骆驼的体温与第一天8时有什么关系吗? 其他时刻呢?
上升:4至16时和28至40时
下降:0至4时,16至28时和40至48时
体温一样
讲授新课
A
温度/℃
时间/时
(5)A点表示的是什么?还有几时的温度与A点所表示的温度相同?
A点表示12时的温度是39℃, 20时、36时及44时的温度与A点所表示的温度相同.
讲授新课
(6)你还知道哪些关于骆驼的趣事?与同伴进行交流.
骆驼非常适合,或者说适应在昼热夜寒、缺少水和绿色植物地上生活,例如非洲的撒哈拉大沙漠或中亚的戈壁滩.
骆驼吃各种植物,甚至包括其他动物碰都不碰的荆棘和含盐的灌木,为寻找食物,它们会长途跋渺.骆驼具有惊人的能力,可以在缺水的情况下行走很长的时间.
归纳总结
拓展:图象(或其局部)如果呈“/”(含“ ”“ ”等)状,
就说明因变量随着自变量的增加而增加.
图象(或其局部)如果呈“\”(含“ ”“ ”等)状,
就表示因变量随着自变量的增加而减少.
图象呈“ ”(含“∧”等)状,表示因变量先随着自变量的增加而增加,然后随着自变量的增加而减少.
图象呈“ ”(含“∨”等)状,表示因变量先随着自变量的增加而减少,然后随着自变量的增加而增加.
讲授新课
三种表示变量之间关系的方法和优缺点:
方法 优点 缺点
表格法 对于表中自变量的每一个值,可以不通过计算,直接把因变量的值找到,查询时很方便,于是一些数学用表应运而生 只能列出部分自变量与因变量的对应值,难以反映变量间变化的全貌,而且从表中看不出变量间的对应规律
关系式法 关系式简明扼要,规范准确 有些变量之间的关系很难或不能用关系式表示,求对应值也需要逐个计算,比较麻烦
图象法 形象直观,可以形象地反映出事物变图象/化的全过程、变化的趋势和某些性质图象是近似的、局部的,由观察图象确定的大或最小值等) 图象是近似的、局部的,由观察图象确定的因变量的值往往不够准确
当堂检测
1.在一次足球比赛中,守门员用脚踢出去的球的高度h随时间t的变化而变化,可以近似地表示h与t的关系的图象是( )
C
当堂检测
2.如图,图象记录了某地一月份某天的温度随时间变化的情况,请你仔细观察图象,根据图中提供的信息,判断不符合图象描述的说法是( )
A.20时的温度约为-1 ℃
B.温度是2 ℃的时刻是12时
C.最暖和的时刻是14时
D.在-3 ℃以下的时间约为8小时
B
当堂检测
3. 下列各情境分别可以用哪幅图来近似刻画 (1)凉水逐渐加热转化为水蒸气跑掉(水温与时间的关系);(2)匀速行驶的火车(速度与时间的关系);(3)运动员推出去的铅球(高度与时间的关系);(4)小明匀速从A地走到B地后逗留一段时间,然后按原速返回(小明距A地的距离与时间的关系).
当堂检测
A是 的图象,
B是 的图象,
C是 的图象,
D是 的图象.(填序号)
(4)
(2)
(1)
(3)
当堂检测
4. 如图所示的图象记录了某地一月份某天的气温随时间变化的情况,请你仔细观察图象回答下面的问题:20时的气温是 ℃;气温是0 ℃的时刻是 时;气温最高的时刻是 时.
-1
12和18
14
当堂检测
5. 如图表示某市2019年6月份某一天的气温随时间变化的情况,请回答下列问题:
(1)这天的最高气温是多少
(2)这天共有几个小时的气温在31 ℃以上
(3)这天在什么时间范围内气温在上升
(4)点A表示的意义是什么 还有几时的气
温与点A表示的气温相同
(5)请你预测,次日凌晨1点的气温大约是 ℃.
当堂检测
解:(1)36 ℃
(2)9个
(3)3~15时
(4)点A表示的意义是12时的气温是31℃;
21时的气温与点A表示的气温相同
(5)25
当堂检测
6.海水受日月的引力而产生潮汐现象,早晨海水上涨叫做潮,黄昏海水上涨叫做汐,合称潮汐.潮汐与人类的生活有着密切的联系.下面是某港口从 0时到12时的水深情况.
当堂检测
(1)大约什么时刻港口的水最深?深度约是多少?
(2)大约什么时刻港口的水最浅?深度约是多少?
(3)在什么时间范围内,港口水深在增加?
大约3时刻港口的水最深,深度约7. 5m
大约9时刻港口的水最浅,深度约是2.4m
0时到3时和9时到12时港口水深在增加
(4)在什么时间范围内,港口水深在减少?
3时到9时港口水深在减少.
当堂检测
(5) A,B 两点分别表示什么?还有几时水的深度与A 点所表示的深度相同?
A点表示6时港口的水深大约为5m,B 点表示12时港口的水深大约为4.3m;0时水的深度与A点所表示的深度相同.
(6) 说一说这个港口从 0 时 到 12 时 的水深是怎样变化的.
0时到3时水深在增加,3时到9时水深在减少,9时到12时水深又在增加.
课堂小结
其特点是直观
变量之间的关系
表格法
关系式法
图象法
从“数”的角度反映
变量之间的关系:
其特点是清楚
从“式”的角度反映
变量之间的关系:
其特点是简单明了
从“形”的角度反映
变量之间的关系:
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
