人教版八下数学第十八章 18.1平行四边形 同步试题(word版含解析)
文档属性
| 名称 | 人教版八下数学第十八章 18.1平行四边形 同步试题(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 158.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 00:00:00 | ||
图片预览




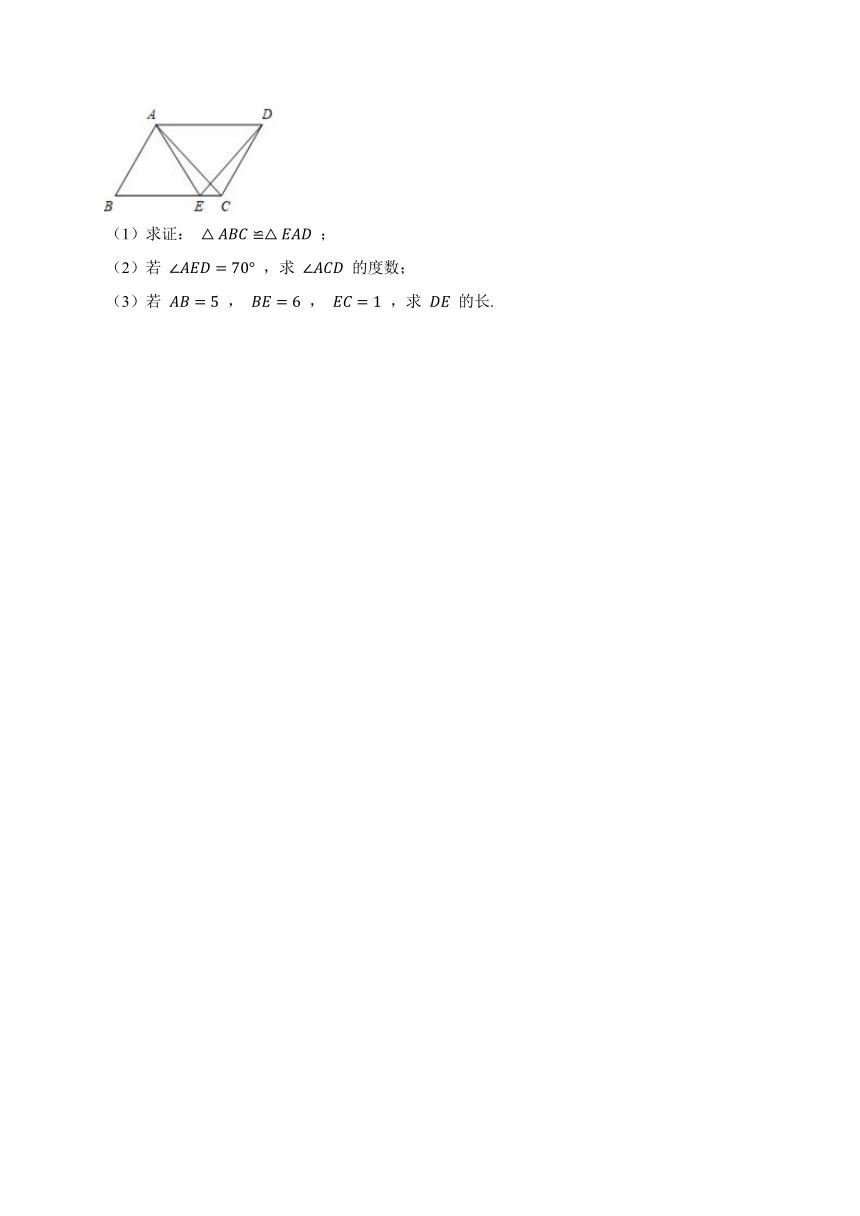
文档简介
18.1平行四边形同步试题
一、单选题
1.(2022八下·)在四边形ABCD中,O是对角线交点,下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AD∥BC,AD=BC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OD=OB
2.(2022八下·)点A,B,C,D在同一平面内,有以下条件:①AB∥DC;②AB=DC;③BC∥AD;④BC=AD。从四个条件中任意选取两个,能使四边形ABCD是平行四边形的选法有 ( )
A.3种 B.4种 C.5种 D.6种
3.(2022八下·)平行四边形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对边平行 D.对边相等
4.(2021八上·大庆期末)如图,已知E为邻边相等的平行四边形ABCD的边BC上一点,且∠DAE=∠B=80 ,那么∠CDE的度数为( )
A.20 B.25 C.30 D.35
5.(2021九上·南宁月考)如图,在 中, , , , 则 的周长是( )
A.16 B.20 C.21 D.23
6.(2021九上·娄底月考)如图,在 中, , , 的平分线 交 于点 ,则 的值是( )
A.1 B.2 C.3 D.4
7.(2022八下·)已知□ABCD的周长为36,且AB:AD=1:2,则AB的长为( )
A.3 B.6 C.12 D.24
8.(2022八下·)在 □ ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.2:1:1:2 B.1:2:2:1 C.2:1:2:1 D.1:1:2:2
9.(2021八上·大庆期末)在□ABCD中,AC=24,BD=38,AB=m,则m的取值范围是( )
A.2410.(2021九上·滕州月考)如图,在平行四边形ABCD中,BC=2AB,∠B=72°,CE⊥AB于E,F为AD中点,则∠AEF等于( )
A.54° B.55° C.60° D.45°
二、填空题
11.(2021八下·相城期末)在 中, ,则 的度数是 .
12.(2021八下·衡阳期末)如图,平行四边形 的周长为 , 的周长为 ,则对角线 的长为 .
13.(2021八上·大庆期末)在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为 .
14.(2021·武汉模拟)在 ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BC=5,则对角线BD= .
15.如图,已知平行四边形ABCD,以点A为圆心,适当长为半径画弧分别交AB,AD于点E,F,再分别以点E,F为圆心,大于 EF的长为半径画弧,两弧在∠DAB的内部相交于点G,画射线AG交DC于H.若∠B=140°,则∠DHA= .
16.如图, □ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连结BE,若 □ ABCD的周长为28,则△ABE的周长为 .
17.(2022八下·)在四边形ABCD中,对角线AC与BD交于点O已知OA=OC,添加①AB=DC,②AB∥DC③OB=OD中的一个不能判定这个四边形是平行四边形的是 。(填序号)
18.(2022八下·)如图,在四边形ABCD中,AD∥BC,AB=CD=2,BC=5,∠BAD的平分线交BC于点E,且AE∥CD,则四边形AECD的面积为 。
19.(2022八下·)如图,P是□ABCD内任意一点,若S□ABCD=16,则阴影部分的面积为 。
20.(2021九上·哈尔滨月考)如图,在平行四边形ABCD中,AD=5,AB=2 ,∠B是锐角,AE⊥BC于点E,F是AB的中点,连接DF,EF,若∠EFD=90°,则AE的长为 .
三、解答题
21.(2021八上·大庆期末)如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
22.(2021·于洪模拟)如图,在中,对角线与相交于点,点,分别在和的延长线上,且,连接,.求证:.
23.(2020八下·长兴期中)如图,在 ABCD中,点O是对角线BD的中点,过点O任作一条直线,分别与AD,BC交于点E,F。
求证:四边形BEDF是平行四边形。
24.如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
四、综合题
25.(2021八下·南平期末)如图,在平行四边形 中, 为 边上一点,且 .
(1)求证: ;
(2)若 ,求 的度数;
(3)若 , , ,求 的长.
答案解析部分
1.【答案】C
【解析】【解答】解:A、∵AD∥BC,AD=BC ,∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形),不符合题意;
B、∵AB=DC,AD=BC,∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形),不符合题意;
C、 AB∥DC,AD=BC ,不能判定四边形ABCD是平行四边形,符合题意;
D、∵OA=OC,OD=OB,∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形),不符合题意;
故答案为:C.
【分析】平行四边形的判定定理有:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;依此分别判断即可.
2.【答案】B
【解析】【解答】解:(1) ①AB∥DC,②AB=DC (一组对边平行且相等的四边形是平行四边形);
(2) ①AB∥DC , ③BC∥AD (两组对边分别平行的四边形是平行四边形);
(3) ②AB=DC , ④BC=AD (两组对边分别相等的四边形是平行四边形);
(4) ③BC∥AD, ④BC=AD (一组对边平行且相等的四边形是平行四边形);
综上,共4种.
故答案为:B.
【分析】根据平行四边形的判定定理有:一组对边平行且相等的四边形是平行四边形;两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;选择条件作答即可.
3.【答案】A
【解析】【解答】解:AB、平行四边形对角线互相平分,但不一定相等,故A错,符合题意,B正确,不符合题意;
CD、平行四边形对边平行且相等,正确,不符合题意;
故答案为:A.
【分析】根据平行四边形的性质,即对边平行且相等,对角线互相平分,分别判断,即可作答.
4.【答案】C
【解析】【解答】∵AD BC,
∴∠AEB=∠DAE=∠B=80°,
∴AE=AB=AD,
在三角形AED中,AE=AD,∠DAE=80°,
∴∠ADE=50°,
又∵∠B=80°,
∴∠ADC=80°,
∴∠CDE=∠ADC-∠ADE=30°.
故答案为:C.
【分析】利用平行四边形的性质得出三角形ABE为等腰三角形,然后求出CDE的度数。
5.【答案】C
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴ ,
∵ , , ,
∴ ,
∴ ,
故答案为:C.
【分析】由平行四边形的性质可得AD=BC,OA=OC,OB=OD,由△AOD的周长=AD+OA+OD可求解.
6.【答案】C
【解析】【解答】解: 四边形是平行四边形,
, ,
,
平分 ,
,
,
,
;
故答案为:C.
【分析】由平行四边形的性质可得AD=BC=7,AD∥BC,由平行线的性质可得∠AEB=∠CBE,由角平分线的概念可得∠ABE=∠CBE,推出∠AEB=∠ABE,得到AE=AB,然后根据DE=AD-AE进行求解.
7.【答案】B
【解析】【解答】解:∵平行四边形ABCD的周长为36,
∴AB=CD,AD=BC
∴2(AB+AD)=36,
∴AB+AD=18;
∵AB:AD=1:2,
∴AD=2AB,
∴3AB=18,
解之:AB=6.
故答案为:B.
【分析】利用平行四边形的性质可证得AB=CD,AD=BC,结合已知可求出AB+AD的长;再根据题意可得到AD=2AB,然后解方程组求出AB的长.
8.【答案】C
【解析】【解答】解:∵平行四边形ABCD,
∴∠A=∠C,∠B=∠D,∠A+∠B=∠C+∠D=180°,
ABD、∠A≠∠C,∠B≠∠D,错误;
C、∠A=∠C,∠B=∠D,∠A+∠B=∠C+∠D,正确;
故答案为:C.
【分析】根据平行四边形的性质得出∠A=∠C,∠B=∠D,∠A+∠B=∠C+∠D=180°,结合每项的条件分别判断,即可解答.
9.【答案】C
【解析】【解答】解:如图所示:
∵四边形ABCD为平行四边形,
∴ , ,
在 中, ,
∴ ,
即 ,
故答案为:C.
【分析】根据平行四边形的性质求出AE、BE的值,然后在ABE中根据三角形的三边关系得出结果。
10.【答案】A
【解析】【解答】解:取BC的中点G,连接EG、FG,如图,
∵四边形ABCD为平行四边形,
∴AD=BC,ADBC,
∴AFBG,
∵F为AD的中点,
∴AF=BG= AD,
∴四边形ABGF是平行四边形,
∴ABFG,
∵四边形ABCD为平行四边形,
∴ABCD,
∴ABFG,
∵CE⊥AB,
∴∠CEB=90°,
∴EG=BG,
∴∠B=∠GEB=∠FGC=72°,
∴∠BGE=180°﹣72°﹣72°=36°,
∴∠EGF=180°﹣72°﹣36°=72°,
∵BC=2AB,
∴EG=AB=FG,
∴∠EFG=∠FEG=54°,
∴∠AEF=180°﹣54°﹣72°=54°,
故答案为:A.
【分析】取BC的中点G,连接EG、FG,如图,先根据直角三角形斜边上的中线的性质得出EG=AB=FG,则∠B=∠GEB=∠FGC=72°,则EG=AB=FG,得出∠EFG=∠FEG,接着利用平角的定义可得出∠AEF大小。
11.【答案】60°
【解析】【解答】解:如图,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠A+∠B=180°,
把∠B=2∠A代入得:3∠A=180°,
∴∠A=60°,
故答案为:60°.
【分析】根据平行四边形的性质得出BC∥AD,根据平行线的性质推出∠A+∠B=180°,代入求出即可.
12.【答案】10
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵平行四边形ABCD的周长是36 cm,
∴AB+BC=18cm,
∵△ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=28-18=10cm.
故答案为:10.
【分析】平行四边的周长c=2(a+b)算出两邻边之和,进而根据三角形周长=a+b+c即可求得AC的长度.
13.【答案】10或14或10
【解析】【解答】解: 四边形ABCD是平行四边形,
, , ,
, ,
BF平分∠ABC, CE平分∠BCD,
, ,
, ,
由等角对等边可知: , ,
情况1:当 与 相交时,如下图所示:
,
,
,
情况2:当 与 不相交时,如下图所示:
,
,
故答案为:10或14.
【分析】根据四边形ABCD是平行四边形,证明= , ,由等角对等边可知: , ,然后分为当 与 相交和当 与 不相交两种情况进行求解。
14.【答案】
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,OB=OD= BD,
∵AB⊥AC,
∴∠BAC=90°,
∴AC= ,
∴OA= AC= ,
∴OB= ,
∴BD=2OB= ;
故答案为: .
【分析】由平行四边形的对角线互相平分得出OA=OC,OB=OD,由勾股定理求出AC,得出OA的长,再由勾股定理求出OB,即可得出对角线BD的长.
15.【答案】20°
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAD=180°﹣140°=40°,
由作法得AH平分∠BAD,
∴∠BAH=∠DAH,
∴∠BAD= ∠BAD=20°,
∵AB∥CD,
∴∠DHA=∠BAH=20°.
故答案为:20°.
【分析】先利用平行四边形的性质得到AB∥CD,AD∥BC,则利用平行线的性质可计算出∠BAD=40°,再由作法得AH平分∠BAD,所以∠BAD= ∠BAD=20°,然后根据平行线的性质得到∠DHA的度数.
16.【答案】14
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴OB=OD,
又OE⊥BD,
∴OE是BD的垂直平分线,
∴BE=ED,
∴BE+AE=ED+AE=AD,
∴△ABE的周长=AB+BE+AE=AB+AD=14.
故答案为:14.
【分析】根据平行四边形的性质得出OB=OD,结合OE⊥BD,得出OE是BD的垂直平分线,则可得到BE=ED,从而把△ABE的周长转化为AB+AD,结合平行四边形的周长,即可解答.
17.【答案】①
【解析】【解答】解:如图,
在四边形ABCD中,
①∵OA=OC,AB=CD, 不能判定这个四边形是平行四边形 ,①符合题意;
②∵OA=OC,AB∥DC,
∴∠ABO=∠CDO,∠BAO=∠CDO,
∴△AOB≌△COD(ASA),
∴AB=CD,
∴四边形ABCD的平行四边形(一组对边平行且相等的四边形是平行四边形),②不符合题意;
③∵OA=OC,OB=OD ,∴四边形ABCD的平行四边形(对角线互相平分的四边形是平行四边形),③不符合题意;
综上,符合题意得是 ① .
故答案为:①.
【分析】根据平行四边形的判定定理,结合各项条件,分别解答判断,即可作答.
18.【答案】
【解析】【解答】解:作AH⊥BE,
∵AD∥BC,AE∥CD,
∴四边形AECD为平行四边形,
∴AE=CD=2,
∵AD∥BC,
∴∠AEB=∠DAE,
∵∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∴AB=BE=AE=2,
∴△ABE是等边三角形,EC=BC-BE=5-2=3,
∴AH=AE=,
∴四边形AECD的面积=EC×AH=3×=3.
故答案为: 3.
【分析】作AH⊥BE,先证明四边形AECD为平行四边形,得出AE=CD=2,再根据平行线的性质和角平分线的定义求出AB=BE,从而求出△ABE是等边三角形和EC的长,再根据等边三角形的性质求出AH长,最后计算平行四边形AECD的面积即可.
19.【答案】8
【解析】【解答】解:过P点分别作EF∥AB,GH∥BC,
则四边形AGPE、四边形BGPF,四边形EPHD,四边形CFPH都是平行四边形,
∴S△AEP=S△AGP(等底等高),
同理S△BGP=S△BFP,S△FCP=S△HCP,S△DEP=S△DHP,
∴S阴影=SABCD=8.
故答案为:8.
【分析】过P点分别作EF∥AB,GH∥BC,把 ABCD 分割成四个平行四边形,然后根据三角形面积等积求出S△BGP=S△BFP,S△FCP=S△HCP,S△DEP=S△DHP,依此解答即可.
20.【答案】
【解析】【解答】解:设 ,
则在RtΔABE中有 ,
如图,延长EF至点G使FG=EF,连接AG、DE、BG,
∵点F是AB的中点,
∴四边形AEBG是平行四边形,
∴AG∥BE,AG=BE=x,
又∵□ABCD中有AD∥BC,
∴G、A、D三点共线,
∴DG=AG+AD=x+5,
∵∠EFD=90°,
∴DF垂直平分EG,
∴DE=DG=x+5,
∵AE⊥BC,AD∥BC,
∴AE⊥AD,
∴ ,
∴
解得 , (舍)
∴ ,
∴ .
故答案为: .
【分析】先求出DF垂直平分EG,再求出,最后求解即可。
21.【答案】解: 四边形 是平行四边形
AB⊥AC,
在 中,
在 中,
【解析】【分析】 在 中,利用勾股定理求出AC,根据平行四边形的性质得出OA=, 在 中, 利用勾股定理求出OB,即可得BD。
22.【答案】证明:四边形是平行四边形,
,,
又
(SAS)
【解析】【分析】根据平行四边形的性质可得OA=OC,OB=OD,结合AE=CF可得OE=OF,根据对顶角的性质可得∠DOE=∠BOF,证明△DOE≌△BOF,据此可得结论.
23.【答案】解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EDB=∠FBD,
在△DOE与△BOF中
∴△DOE≌△BOF(ASA),
∴OE=OF,又∵OB=OD,∴四边形BEDF是平行四边形
【解析】【分析】根据平行四边形的判定定理:对角线互相平分的四边形是平行四边形。根据三角形的全等,得出OE=OF ,根据平行四边形的性质得 OB=OD ,进而判断出四边形BEDF是平行四边形。
24.【答案】解:①以PQAD构成四边形
设X秒成为平行四边形
根据题意得:
x=24﹣3x
∴x=6
∴当运动6s时成为平行四边形;
②以PQBC构成四边形
设Y秒成为平行四边形
根据题意得:
10﹣y=3y
∴y=2.5
∴当运动2.5s时也成为平行四边形.
③四边形PAQC、四边形PDQB其实也可能成为平行四边形,其中,PDQB是错误的,四边形PAQC成为平行四边形时是7秒.
故答案为6秒、2.5秒、7秒
【解析】【分析】根据题意P,Q和梯形ABCD的两个顶点构成平行四边形,分两种情况讨论:①可以构成四边形PQAD;②可以构成四边形PQBC两种.
25.【答案】(1)证明:∵四边形 是平行四边形,
∴ , ,
∴ ,
∵ ,
∴ ,
∴ ,
在 和 中
,
∴ .
(2)解:由(1)得△ABC≌△EAD,
∴∠BAC=∠AED=70°,
∵四边形ABCD是平行四边形,
∴AB//DC,
∴∠ACD=∠BAC=70°;
(3)解:如图,过点 作 于点 ,
∵ ,
∴ , ,
在 和 中,由勾股定理得:
, ,
由(1)得 ,
∴ .
【解析】【分析】(1) △ABC和△EAD中已经有一条边和一个角分别相等,根据平行的性质和等边对等角得出∠B=∠DAE即可证明.
(2)根据全等三角形的性质,利用平行四边形的性质求解即可.
(3) 如图,过点 作 于点 ,根据等腰三角形的三线合一性质得到 ,接着根据勾股定理性质及全等性质即可求解
一、单选题
1.(2022八下·)在四边形ABCD中,O是对角线交点,下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AD∥BC,AD=BC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OD=OB
2.(2022八下·)点A,B,C,D在同一平面内,有以下条件:①AB∥DC;②AB=DC;③BC∥AD;④BC=AD。从四个条件中任意选取两个,能使四边形ABCD是平行四边形的选法有 ( )
A.3种 B.4种 C.5种 D.6种
3.(2022八下·)平行四边形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对边平行 D.对边相等
4.(2021八上·大庆期末)如图,已知E为邻边相等的平行四边形ABCD的边BC上一点,且∠DAE=∠B=80 ,那么∠CDE的度数为( )
A.20 B.25 C.30 D.35
5.(2021九上·南宁月考)如图,在 中, , , , 则 的周长是( )
A.16 B.20 C.21 D.23
6.(2021九上·娄底月考)如图,在 中, , , 的平分线 交 于点 ,则 的值是( )
A.1 B.2 C.3 D.4
7.(2022八下·)已知□ABCD的周长为36,且AB:AD=1:2,则AB的长为( )
A.3 B.6 C.12 D.24
8.(2022八下·)在 □ ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.2:1:1:2 B.1:2:2:1 C.2:1:2:1 D.1:1:2:2
9.(2021八上·大庆期末)在□ABCD中,AC=24,BD=38,AB=m,则m的取值范围是( )
A.24
A.54° B.55° C.60° D.45°
二、填空题
11.(2021八下·相城期末)在 中, ,则 的度数是 .
12.(2021八下·衡阳期末)如图,平行四边形 的周长为 , 的周长为 ,则对角线 的长为 .
13.(2021八上·大庆期末)在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为 .
14.(2021·武汉模拟)在 ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BC=5,则对角线BD= .
15.如图,已知平行四边形ABCD,以点A为圆心,适当长为半径画弧分别交AB,AD于点E,F,再分别以点E,F为圆心,大于 EF的长为半径画弧,两弧在∠DAB的内部相交于点G,画射线AG交DC于H.若∠B=140°,则∠DHA= .
16.如图, □ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连结BE,若 □ ABCD的周长为28,则△ABE的周长为 .
17.(2022八下·)在四边形ABCD中,对角线AC与BD交于点O已知OA=OC,添加①AB=DC,②AB∥DC③OB=OD中的一个不能判定这个四边形是平行四边形的是 。(填序号)
18.(2022八下·)如图,在四边形ABCD中,AD∥BC,AB=CD=2,BC=5,∠BAD的平分线交BC于点E,且AE∥CD,则四边形AECD的面积为 。
19.(2022八下·)如图,P是□ABCD内任意一点,若S□ABCD=16,则阴影部分的面积为 。
20.(2021九上·哈尔滨月考)如图,在平行四边形ABCD中,AD=5,AB=2 ,∠B是锐角,AE⊥BC于点E,F是AB的中点,连接DF,EF,若∠EFD=90°,则AE的长为 .
三、解答题
21.(2021八上·大庆期末)如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
22.(2021·于洪模拟)如图,在中,对角线与相交于点,点,分别在和的延长线上,且,连接,.求证:.
23.(2020八下·长兴期中)如图,在 ABCD中,点O是对角线BD的中点,过点O任作一条直线,分别与AD,BC交于点E,F。
求证:四边形BEDF是平行四边形。
24.如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
四、综合题
25.(2021八下·南平期末)如图,在平行四边形 中, 为 边上一点,且 .
(1)求证: ;
(2)若 ,求 的度数;
(3)若 , , ,求 的长.
答案解析部分
1.【答案】C
【解析】【解答】解:A、∵AD∥BC,AD=BC ,∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形),不符合题意;
B、∵AB=DC,AD=BC,∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形),不符合题意;
C、 AB∥DC,AD=BC ,不能判定四边形ABCD是平行四边形,符合题意;
D、∵OA=OC,OD=OB,∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形),不符合题意;
故答案为:C.
【分析】平行四边形的判定定理有:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;依此分别判断即可.
2.【答案】B
【解析】【解答】解:(1) ①AB∥DC,②AB=DC (一组对边平行且相等的四边形是平行四边形);
(2) ①AB∥DC , ③BC∥AD (两组对边分别平行的四边形是平行四边形);
(3) ②AB=DC , ④BC=AD (两组对边分别相等的四边形是平行四边形);
(4) ③BC∥AD, ④BC=AD (一组对边平行且相等的四边形是平行四边形);
综上,共4种.
故答案为:B.
【分析】根据平行四边形的判定定理有:一组对边平行且相等的四边形是平行四边形;两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;选择条件作答即可.
3.【答案】A
【解析】【解答】解:AB、平行四边形对角线互相平分,但不一定相等,故A错,符合题意,B正确,不符合题意;
CD、平行四边形对边平行且相等,正确,不符合题意;
故答案为:A.
【分析】根据平行四边形的性质,即对边平行且相等,对角线互相平分,分别判断,即可作答.
4.【答案】C
【解析】【解答】∵AD BC,
∴∠AEB=∠DAE=∠B=80°,
∴AE=AB=AD,
在三角形AED中,AE=AD,∠DAE=80°,
∴∠ADE=50°,
又∵∠B=80°,
∴∠ADC=80°,
∴∠CDE=∠ADC-∠ADE=30°.
故答案为:C.
【分析】利用平行四边形的性质得出三角形ABE为等腰三角形,然后求出CDE的度数。
5.【答案】C
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴ ,
∵ , , ,
∴ ,
∴ ,
故答案为:C.
【分析】由平行四边形的性质可得AD=BC,OA=OC,OB=OD,由△AOD的周长=AD+OA+OD可求解.
6.【答案】C
【解析】【解答】解: 四边形是平行四边形,
, ,
,
平分 ,
,
,
,
;
故答案为:C.
【分析】由平行四边形的性质可得AD=BC=7,AD∥BC,由平行线的性质可得∠AEB=∠CBE,由角平分线的概念可得∠ABE=∠CBE,推出∠AEB=∠ABE,得到AE=AB,然后根据DE=AD-AE进行求解.
7.【答案】B
【解析】【解答】解:∵平行四边形ABCD的周长为36,
∴AB=CD,AD=BC
∴2(AB+AD)=36,
∴AB+AD=18;
∵AB:AD=1:2,
∴AD=2AB,
∴3AB=18,
解之:AB=6.
故答案为:B.
【分析】利用平行四边形的性质可证得AB=CD,AD=BC,结合已知可求出AB+AD的长;再根据题意可得到AD=2AB,然后解方程组求出AB的长.
8.【答案】C
【解析】【解答】解:∵平行四边形ABCD,
∴∠A=∠C,∠B=∠D,∠A+∠B=∠C+∠D=180°,
ABD、∠A≠∠C,∠B≠∠D,错误;
C、∠A=∠C,∠B=∠D,∠A+∠B=∠C+∠D,正确;
故答案为:C.
【分析】根据平行四边形的性质得出∠A=∠C,∠B=∠D,∠A+∠B=∠C+∠D=180°,结合每项的条件分别判断,即可解答.
9.【答案】C
【解析】【解答】解:如图所示:
∵四边形ABCD为平行四边形,
∴ , ,
在 中, ,
∴ ,
即 ,
故答案为:C.
【分析】根据平行四边形的性质求出AE、BE的值,然后在ABE中根据三角形的三边关系得出结果。
10.【答案】A
【解析】【解答】解:取BC的中点G,连接EG、FG,如图,
∵四边形ABCD为平行四边形,
∴AD=BC,ADBC,
∴AFBG,
∵F为AD的中点,
∴AF=BG= AD,
∴四边形ABGF是平行四边形,
∴ABFG,
∵四边形ABCD为平行四边形,
∴ABCD,
∴ABFG,
∵CE⊥AB,
∴∠CEB=90°,
∴EG=BG,
∴∠B=∠GEB=∠FGC=72°,
∴∠BGE=180°﹣72°﹣72°=36°,
∴∠EGF=180°﹣72°﹣36°=72°,
∵BC=2AB,
∴EG=AB=FG,
∴∠EFG=∠FEG=54°,
∴∠AEF=180°﹣54°﹣72°=54°,
故答案为:A.
【分析】取BC的中点G,连接EG、FG,如图,先根据直角三角形斜边上的中线的性质得出EG=AB=FG,则∠B=∠GEB=∠FGC=72°,则EG=AB=FG,得出∠EFG=∠FEG,接着利用平角的定义可得出∠AEF大小。
11.【答案】60°
【解析】【解答】解:如图,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠A+∠B=180°,
把∠B=2∠A代入得:3∠A=180°,
∴∠A=60°,
故答案为:60°.
【分析】根据平行四边形的性质得出BC∥AD,根据平行线的性质推出∠A+∠B=180°,代入求出即可.
12.【答案】10
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵平行四边形ABCD的周长是36 cm,
∴AB+BC=18cm,
∵△ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=28-18=10cm.
故答案为:10.
【分析】平行四边的周长c=2(a+b)算出两邻边之和,进而根据三角形周长=a+b+c即可求得AC的长度.
13.【答案】10或14或10
【解析】【解答】解: 四边形ABCD是平行四边形,
, , ,
, ,
BF平分∠ABC, CE平分∠BCD,
, ,
, ,
由等角对等边可知: , ,
情况1:当 与 相交时,如下图所示:
,
,
,
情况2:当 与 不相交时,如下图所示:
,
,
故答案为:10或14.
【分析】根据四边形ABCD是平行四边形,证明= , ,由等角对等边可知: , ,然后分为当 与 相交和当 与 不相交两种情况进行求解。
14.【答案】
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,OB=OD= BD,
∵AB⊥AC,
∴∠BAC=90°,
∴AC= ,
∴OA= AC= ,
∴OB= ,
∴BD=2OB= ;
故答案为: .
【分析】由平行四边形的对角线互相平分得出OA=OC,OB=OD,由勾股定理求出AC,得出OA的长,再由勾股定理求出OB,即可得出对角线BD的长.
15.【答案】20°
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAD=180°﹣140°=40°,
由作法得AH平分∠BAD,
∴∠BAH=∠DAH,
∴∠BAD= ∠BAD=20°,
∵AB∥CD,
∴∠DHA=∠BAH=20°.
故答案为:20°.
【分析】先利用平行四边形的性质得到AB∥CD,AD∥BC,则利用平行线的性质可计算出∠BAD=40°,再由作法得AH平分∠BAD,所以∠BAD= ∠BAD=20°,然后根据平行线的性质得到∠DHA的度数.
16.【答案】14
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴OB=OD,
又OE⊥BD,
∴OE是BD的垂直平分线,
∴BE=ED,
∴BE+AE=ED+AE=AD,
∴△ABE的周长=AB+BE+AE=AB+AD=14.
故答案为:14.
【分析】根据平行四边形的性质得出OB=OD,结合OE⊥BD,得出OE是BD的垂直平分线,则可得到BE=ED,从而把△ABE的周长转化为AB+AD,结合平行四边形的周长,即可解答.
17.【答案】①
【解析】【解答】解:如图,
在四边形ABCD中,
①∵OA=OC,AB=CD, 不能判定这个四边形是平行四边形 ,①符合题意;
②∵OA=OC,AB∥DC,
∴∠ABO=∠CDO,∠BAO=∠CDO,
∴△AOB≌△COD(ASA),
∴AB=CD,
∴四边形ABCD的平行四边形(一组对边平行且相等的四边形是平行四边形),②不符合题意;
③∵OA=OC,OB=OD ,∴四边形ABCD的平行四边形(对角线互相平分的四边形是平行四边形),③不符合题意;
综上,符合题意得是 ① .
故答案为:①.
【分析】根据平行四边形的判定定理,结合各项条件,分别解答判断,即可作答.
18.【答案】
【解析】【解答】解:作AH⊥BE,
∵AD∥BC,AE∥CD,
∴四边形AECD为平行四边形,
∴AE=CD=2,
∵AD∥BC,
∴∠AEB=∠DAE,
∵∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∴AB=BE=AE=2,
∴△ABE是等边三角形,EC=BC-BE=5-2=3,
∴AH=AE=,
∴四边形AECD的面积=EC×AH=3×=3.
故答案为: 3.
【分析】作AH⊥BE,先证明四边形AECD为平行四边形,得出AE=CD=2,再根据平行线的性质和角平分线的定义求出AB=BE,从而求出△ABE是等边三角形和EC的长,再根据等边三角形的性质求出AH长,最后计算平行四边形AECD的面积即可.
19.【答案】8
【解析】【解答】解:过P点分别作EF∥AB,GH∥BC,
则四边形AGPE、四边形BGPF,四边形EPHD,四边形CFPH都是平行四边形,
∴S△AEP=S△AGP(等底等高),
同理S△BGP=S△BFP,S△FCP=S△HCP,S△DEP=S△DHP,
∴S阴影=SABCD=8.
故答案为:8.
【分析】过P点分别作EF∥AB,GH∥BC,把 ABCD 分割成四个平行四边形,然后根据三角形面积等积求出S△BGP=S△BFP,S△FCP=S△HCP,S△DEP=S△DHP,依此解答即可.
20.【答案】
【解析】【解答】解:设 ,
则在RtΔABE中有 ,
如图,延长EF至点G使FG=EF,连接AG、DE、BG,
∵点F是AB的中点,
∴四边形AEBG是平行四边形,
∴AG∥BE,AG=BE=x,
又∵□ABCD中有AD∥BC,
∴G、A、D三点共线,
∴DG=AG+AD=x+5,
∵∠EFD=90°,
∴DF垂直平分EG,
∴DE=DG=x+5,
∵AE⊥BC,AD∥BC,
∴AE⊥AD,
∴ ,
∴
解得 , (舍)
∴ ,
∴ .
故答案为: .
【分析】先求出DF垂直平分EG,再求出,最后求解即可。
21.【答案】解: 四边形 是平行四边形
AB⊥AC,
在 中,
在 中,
【解析】【分析】 在 中,利用勾股定理求出AC,根据平行四边形的性质得出OA=, 在 中, 利用勾股定理求出OB,即可得BD。
22.【答案】证明:四边形是平行四边形,
,,
又
(SAS)
【解析】【分析】根据平行四边形的性质可得OA=OC,OB=OD,结合AE=CF可得OE=OF,根据对顶角的性质可得∠DOE=∠BOF,证明△DOE≌△BOF,据此可得结论.
23.【答案】解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EDB=∠FBD,
在△DOE与△BOF中
∴△DOE≌△BOF(ASA),
∴OE=OF,又∵OB=OD,∴四边形BEDF是平行四边形
【解析】【分析】根据平行四边形的判定定理:对角线互相平分的四边形是平行四边形。根据三角形的全等,得出OE=OF ,根据平行四边形的性质得 OB=OD ,进而判断出四边形BEDF是平行四边形。
24.【答案】解:①以PQAD构成四边形
设X秒成为平行四边形
根据题意得:
x=24﹣3x
∴x=6
∴当运动6s时成为平行四边形;
②以PQBC构成四边形
设Y秒成为平行四边形
根据题意得:
10﹣y=3y
∴y=2.5
∴当运动2.5s时也成为平行四边形.
③四边形PAQC、四边形PDQB其实也可能成为平行四边形,其中,PDQB是错误的,四边形PAQC成为平行四边形时是7秒.
故答案为6秒、2.5秒、7秒
【解析】【分析】根据题意P,Q和梯形ABCD的两个顶点构成平行四边形,分两种情况讨论:①可以构成四边形PQAD;②可以构成四边形PQBC两种.
25.【答案】(1)证明:∵四边形 是平行四边形,
∴ , ,
∴ ,
∵ ,
∴ ,
∴ ,
在 和 中
,
∴ .
(2)解:由(1)得△ABC≌△EAD,
∴∠BAC=∠AED=70°,
∵四边形ABCD是平行四边形,
∴AB//DC,
∴∠ACD=∠BAC=70°;
(3)解:如图,过点 作 于点 ,
∵ ,
∴ , ,
在 和 中,由勾股定理得:
, ,
由(1)得 ,
∴ .
【解析】【分析】(1) △ABC和△EAD中已经有一条边和一个角分别相等,根据平行的性质和等边对等角得出∠B=∠DAE即可证明.
(2)根据全等三角形的性质,利用平行四边形的性质求解即可.
(3) 如图,过点 作 于点 ,根据等腰三角形的三线合一性质得到 ,接着根据勾股定理性质及全等性质即可求解
