人教版七年级下册5.1.1相交线 课件(共21张PPT)
文档属性
| 名称 | 人教版七年级下册5.1.1相交线 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 292.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 15:02:17 | ||
图片预览







文档简介
(共21张PPT)
第五章 相交线与平行线
5.1.1相交线
人教版七年级数学下册
备课组:七年级数学组
议课时间:2022.2.20
授课时间:2022.2(第1周)
1、能找出图形中一个角的邻补角和对顶角;
学习目标(1分钟)
2、掌握对顶角、邻补角的概念及性质,
并能进行简单的应用.(重难点)
定义:有 , 且两边 的两个角叫对顶角.
性质: .
自学指导1(1分钟)
学生自学 教师巡视(7分钟)
认真阅读课本P2的内容,并划出概念中的关键字眼:
2、什么是对顶角?对顶角有什么性质?
公共顶点
互为反向延长线
对顶角相等
1、什么是邻补角?邻补角有什么性质?
定义:有 ,另一边 的
两个角叫邻补角.
性质: .
一条公共边
互为反向延长线
邻补角和为180°(邻补角互补)
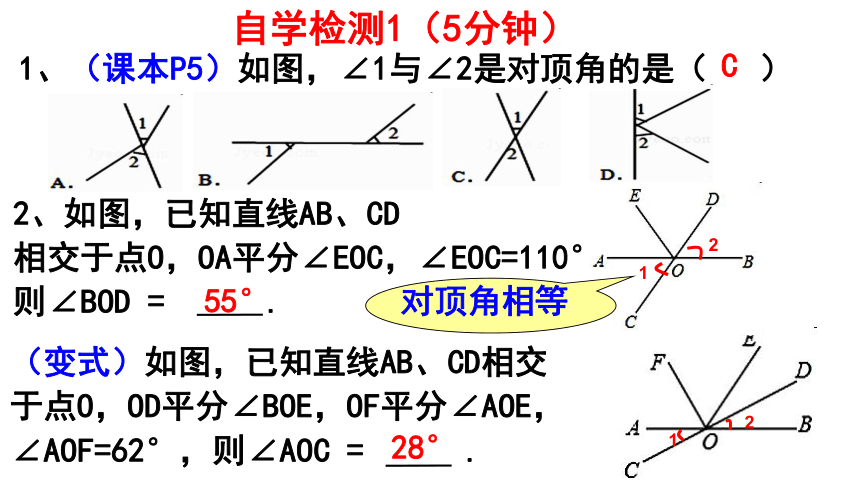
自学检测1(5分钟)
1、(课本P5)如图,∠1与∠2是对顶角的是( )
C
2、如图,已知直线AB、CD
相交于点O,OA平分∠EOC,∠EOC=110°,
则∠BOD = .
55°
1
2
对顶角相等
(变式)如图,已知直线AB、CD相交
于点O,OD平分∠BOE,OF平分∠AOE,
∠AOF=62°,则∠AOC = .
1
2
28°
① 有公共顶点;
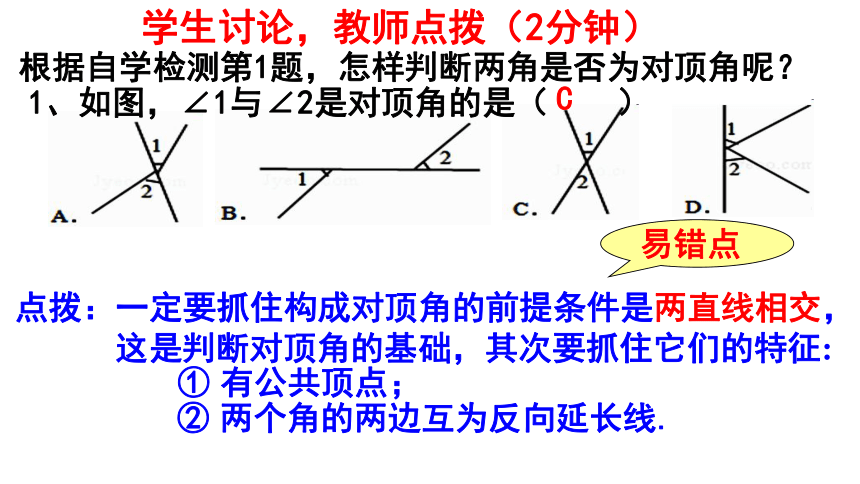
学生讨论,教师点拨(2分钟)
1、如图,∠1与∠2是对顶角的是( )
C
根据自学检测第1题,怎样判断两角是否为对顶角呢?
点拨:一定要抓住构成对顶角的前提条件是两直线相交,
这是判断对顶角的基础,其次要抓住它们的特征:
② 两个角的两边互为反向延长线.
易错点
自学指导2(1分钟)
认真阅读课本P3的例1:
学生自学 教师巡视(5分钟)
例1、如图,直线a、b相交,∠1=40°,
求 ∠2、∠3、∠ 4的度数.
a
b
)
(
1
3
4
2
)
(
(对顶角相等)
∵∠3=∠1
∠1=40°( )
已知
∴∠3=40°
解:
(等量代换)
∴∠2=180°—∠1=140°
∴∠4=∠2=140°
(对顶角相等)
(邻补角的定义)
自学检测2(5分钟)
直线AB、CD相交于O, ∠AOC=80°∠1=30°;
求∠2的度数.
A
C
E
1
2
)
)
O
解:∵∠DOB=∠ ,( )
=80°(已知)
∴∠DOB= °(等量代换)
又∵∠1=30°( )
∴∠2=∠ -∠
= - = °
AOC
∠AOC
DOB
80°
30°
50
对顶角相等
已知
80
D
B
1
课堂小结(2分钟)
角的 名称 特 征 性 质 相 同 点 不 同 点
对 顶 角
邻 补 角
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对,邻补角有四对
①有无公共边
2、(2020秋 召陵区期末)如图,直线AB、CD相交于点E,EF平分∠AEB,若∠BED : ∠DEF= 1 : 2,则∠BEC的度数为( )
A、144° B、126°
C、150° D、72°
C
140°
当堂训练(15分钟)
40°
(变式)互为补角的两个角的度数之比
为2:7,则这两个角的度数分别为 、 .
1、如图1,直线a,b相交于一点,若∠1=70°,则∠2的度数是( )
A.110° B.70° C.90° D.130°
A
解:∵∠2=∠ ( )
∠1=70 °( )
∴∠2= (等量代换)
又∵ (已知)
∴∠3= ( )
∴∠4=180°-∠ = ( 的定义)
3.直线AB、CD交EF于点G、H,∠2=∠3,∠1=70度.求∠4的度数.
A
C
D
B
E
F
G
H
1
2
3
4
图1
1
对顶角相等
已知
70°
∠2=∠3
70 °
等量代换
3
110 °
邻补角
4.直线AB、CD、EF相交于点O,
则∠1+∠2+∠3 = .
180°
5、如图3,直线AB,CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.
(1)写出图中任意一对邻补角;
(2)求∠EOF的度数.
O
A
B
C
D
E
F
(选做题)如图4所示,直线AB、CD、EF相交于点O,形成的对顶角( )
A、3对 B、4对 C、5对 D、6对
图4
正本作业:课本P8,T2
图3
5、如图3,直线AB,CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.
(1)写出图中任意一对邻补角;
(2)求∠EOF的度数.
解:(1)邻补角有:∠DOB与∠DOA∠COB与∠COA , ∠DOE与∠COA等
∴∠EOF=∠DOF-∠DOE= 90°﹣36°= 54°.
(2)依题意,得∠BOD=∠AOC=72°(对顶角相等)
∵OE平分∠BOD ,(已知)
∴∠DOE=
∠BOD= ×72°= 36°(角平分线的定义)
因此,∠EOF的度数是54°.
(选做题)如图4所示,直线AB、CD、EF相交于点O,形成的对顶角有( )
A、3对 B、4对
C、5对 D、6对
图4
O
A
B
C
D
E
F
D
解析:对顶角有6对,分别是:
∠1与∠4、∠BOC与∠AOD
∠2与∠5、∠COF与∠DOE
∠3与∠6、∠AOF与∠BOE
1
2
6
5
4
3
板书设计
5.1.1 两条直线的位置关系
定义:有 ,且两边 的两个
角叫对顶角.
性质: .
公共顶点
互为反向延长线
对顶角相等
定义:有 ,另一边 的
两个角叫邻补角.
性质: .
一条公共边
互为反向延长线
邻补角和为180°
1、邻补角
2、对顶角
有一个公共点的两条直线形成相交直线.
请你画出任意两条相交直线.看看这四个角有什么关系?
问题:两条相交直线.形成的小于平角的角有几个?
1
2
3
4
A
B
C
D
形如∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
O
图中还有哪些角也是邻补角呢?
1
2
3
4
A
B
C
D
O
图中还有哪些角也是对顶角呢?
形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
O
A
B
C
D
)
(
1
3
4
2
)
(
O
A
B
C
D
)
(
1
3
4
2
)
(
有关概念:
邻补角:如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
对顶角:如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
O
A
B
C
D
对顶角相等
4
3
2
1
∠1 与∠3在数量上又有什么关系呢?
∵∠1+∠2=180°
∠3+∠2=180°
∴∠1=∠3(同角的补角相等)
第五章 相交线与平行线
5.1.1相交线
人教版七年级数学下册
备课组:七年级数学组
议课时间:2022.2.20
授课时间:2022.2(第1周)
1、能找出图形中一个角的邻补角和对顶角;
学习目标(1分钟)
2、掌握对顶角、邻补角的概念及性质,
并能进行简单的应用.(重难点)
定义:有 , 且两边 的两个角叫对顶角.
性质: .
自学指导1(1分钟)
学生自学 教师巡视(7分钟)
认真阅读课本P2的内容,并划出概念中的关键字眼:
2、什么是对顶角?对顶角有什么性质?
公共顶点
互为反向延长线
对顶角相等
1、什么是邻补角?邻补角有什么性质?
定义:有 ,另一边 的
两个角叫邻补角.
性质: .
一条公共边
互为反向延长线
邻补角和为180°(邻补角互补)
自学检测1(5分钟)
1、(课本P5)如图,∠1与∠2是对顶角的是( )
C
2、如图,已知直线AB、CD
相交于点O,OA平分∠EOC,∠EOC=110°,
则∠BOD = .
55°
1
2
对顶角相等
(变式)如图,已知直线AB、CD相交
于点O,OD平分∠BOE,OF平分∠AOE,
∠AOF=62°,则∠AOC = .
1
2
28°
① 有公共顶点;
学生讨论,教师点拨(2分钟)
1、如图,∠1与∠2是对顶角的是( )
C
根据自学检测第1题,怎样判断两角是否为对顶角呢?
点拨:一定要抓住构成对顶角的前提条件是两直线相交,
这是判断对顶角的基础,其次要抓住它们的特征:
② 两个角的两边互为反向延长线.
易错点
自学指导2(1分钟)
认真阅读课本P3的例1:
学生自学 教师巡视(5分钟)
例1、如图,直线a、b相交,∠1=40°,
求 ∠2、∠3、∠ 4的度数.
a
b
)
(
1
3
4
2
)
(
(对顶角相等)
∵∠3=∠1
∠1=40°( )
已知
∴∠3=40°
解:
(等量代换)
∴∠2=180°—∠1=140°
∴∠4=∠2=140°
(对顶角相等)
(邻补角的定义)
自学检测2(5分钟)
直线AB、CD相交于O, ∠AOC=80°∠1=30°;
求∠2的度数.
A
C
E
1
2
)
)
O
解:∵∠DOB=∠ ,( )
=80°(已知)
∴∠DOB= °(等量代换)
又∵∠1=30°( )
∴∠2=∠ -∠
= - = °
AOC
∠AOC
DOB
80°
30°
50
对顶角相等
已知
80
D
B
1
课堂小结(2分钟)
角的 名称 特 征 性 质 相 同 点 不 同 点
对 顶 角
邻 补 角
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对,邻补角有四对
①有无公共边
2、(2020秋 召陵区期末)如图,直线AB、CD相交于点E,EF平分∠AEB,若∠BED : ∠DEF= 1 : 2,则∠BEC的度数为( )
A、144° B、126°
C、150° D、72°
C
140°
当堂训练(15分钟)
40°
(变式)互为补角的两个角的度数之比
为2:7,则这两个角的度数分别为 、 .
1、如图1,直线a,b相交于一点,若∠1=70°,则∠2的度数是( )
A.110° B.70° C.90° D.130°
A
解:∵∠2=∠ ( )
∠1=70 °( )
∴∠2= (等量代换)
又∵ (已知)
∴∠3= ( )
∴∠4=180°-∠ = ( 的定义)
3.直线AB、CD交EF于点G、H,∠2=∠3,∠1=70度.求∠4的度数.
A
C
D
B
E
F
G
H
1
2
3
4
图1
1
对顶角相等
已知
70°
∠2=∠3
70 °
等量代换
3
110 °
邻补角
4.直线AB、CD、EF相交于点O,
则∠1+∠2+∠3 = .
180°
5、如图3,直线AB,CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.
(1)写出图中任意一对邻补角;
(2)求∠EOF的度数.
O
A
B
C
D
E
F
(选做题)如图4所示,直线AB、CD、EF相交于点O,形成的对顶角( )
A、3对 B、4对 C、5对 D、6对
图4
正本作业:课本P8,T2
图3
5、如图3,直线AB,CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.
(1)写出图中任意一对邻补角;
(2)求∠EOF的度数.
解:(1)邻补角有:∠DOB与∠DOA∠COB与∠COA , ∠DOE与∠COA等
∴∠EOF=∠DOF-∠DOE= 90°﹣36°= 54°.
(2)依题意,得∠BOD=∠AOC=72°(对顶角相等)
∵OE平分∠BOD ,(已知)
∴∠DOE=
∠BOD= ×72°= 36°(角平分线的定义)
因此,∠EOF的度数是54°.
(选做题)如图4所示,直线AB、CD、EF相交于点O,形成的对顶角有( )
A、3对 B、4对
C、5对 D、6对
图4
O
A
B
C
D
E
F
D
解析:对顶角有6对,分别是:
∠1与∠4、∠BOC与∠AOD
∠2与∠5、∠COF与∠DOE
∠3与∠6、∠AOF与∠BOE
1
2
6
5
4
3
板书设计
5.1.1 两条直线的位置关系
定义:有 ,且两边 的两个
角叫对顶角.
性质: .
公共顶点
互为反向延长线
对顶角相等
定义:有 ,另一边 的
两个角叫邻补角.
性质: .
一条公共边
互为反向延长线
邻补角和为180°
1、邻补角
2、对顶角
有一个公共点的两条直线形成相交直线.
请你画出任意两条相交直线.看看这四个角有什么关系?
问题:两条相交直线.形成的小于平角的角有几个?
1
2
3
4
A
B
C
D
形如∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
O
图中还有哪些角也是邻补角呢?
1
2
3
4
A
B
C
D
O
图中还有哪些角也是对顶角呢?
形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
O
A
B
C
D
)
(
1
3
4
2
)
(
O
A
B
C
D
)
(
1
3
4
2
)
(
有关概念:
邻补角:如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
对顶角:如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
O
A
B
C
D
对顶角相等
4
3
2
1
∠1 与∠3在数量上又有什么关系呢?
∵∠1+∠2=180°
∠3+∠2=180°
∴∠1=∠3(同角的补角相等)
