第六章 圆周运动单元练习(Word版含答案)
文档属性
| 名称 | 第六章 圆周运动单元练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 521.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-08 08:09:02 | ||
图片预览




文档简介
第六章圆周运动单元练习
一、单选题
1.对于做匀速圆周运动的物体,不断变化的物理量是( )
A.周期 B.角速度 C.向心加速度 D.线速度的大小
2.甲、乙两物体做匀速圆周运动,其质量之比为1:2,转动半径之比为1:2,在相等时间里甲转过60°,乙转过45°,则它们所受合外力之比为( )
A.1:4 B.2:3 C.4:9 D.9:16
3.一质量为m的物体,沿半径为R的向下凹的半圆形轨道滑行,如图所示,经过最低点时的速度为v,物体与轨道之间的动摩擦因数为μ,则它在最低点时受到的摩擦力为( )
A.μmg B. C. D.
4.如图所示,光滑杆偏离竖直方向的夹角为,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动。当杆角速度为ω1时,小球的旋转平面在A处,线速度为v1,球对杆的压力为N1;当杆角速度为ω2时,小球的旋转平面在B处,线速度为v2,球对杆的压力为N2,则有( )
A.N1=N2 B.N1v2 D.ω1<ω2
5.在如图所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是。若皮带不打滑,则A、B、C三轮边缘上a、b、c三点的( )
A.角速度之比为2:1:2
B.线速度大小之比为2:1:2
C.周期之比为2:1:1
D.向心加速度之比为1:2:2
6.如图所示,A、B、C 三个物体放在水平旋转圆台上,动摩擦因数均为μ,A的质量为2m,B、C 的质量均为m,A、B离轴的距离为R,C离轴的距离为2R,当慢慢增加圆台转速,最先滑动的是 ( )
A.A B.B C.C D.三个物体同时滑动
7.如图所示,质量为m的小球用长为L的细线悬于O点,细线与竖直方向的夹角为θ,使小球在水平面内以P为圆心做匀速圆周运动,角速度为ω,则下列正确的是( )
A.由于小球做匀速圆周运动,所以加速度不变
B.小球做匀速圆周运动过程中,动能不断变化
C.小球做匀速圆周运动的向心力大小为mω2L
D.细线对小球的拉力大小为mω2L
8.如图,一硬币(可视为质点)置于水平圆盘上,硬币与竖直转轴的距离为r,已知硬币与圆盘之间的动摩擦因数为(最大静摩擦力等于滑动摩擦力),重力加速度大小为g。若硬币与圆盘一起轴匀速转动,则圆盘转动的最大角速度为( )
A. B. C. D.
9.长度为0.5m的轻质细杆OA,A端有一质量为2kg的小球,以O点为圆心,在竖直平面内做圆周运动,如图所示,小球通过最高点时的速度为2m/s,取g=10m/s2,则此时轻杆OA将( )
A.受到4N的拉力 B.受到4N的压力
C.受到36N的拉力 D.受到36N的压力
二、多选题
10.下列说法正确的是
A.做平抛运动的物体,每秒钟速度的改变量一定相等
B.做圆周运动的物体,所受合外力的方向一定与速度方向垂直
C.做圆周运动的物体,向心加速度的方向一定与速度方向垂直
D.做圆周运动的物体,所受的合外力等于圆周运动所需的向心力
11.甲乙两物体都在做匀速圆周运动,在这四种情况下哪个物体的向心加速度比较大
A.线速度相等,乙的半径小,乙的向心加速度较大
B.周期相等,甲的半径大,甲的向心加速度较大
C.角速度相等,乙的线速度小,乙的向心加速度较大
D.半径相等,甲的转速小,甲的向心加速度较大
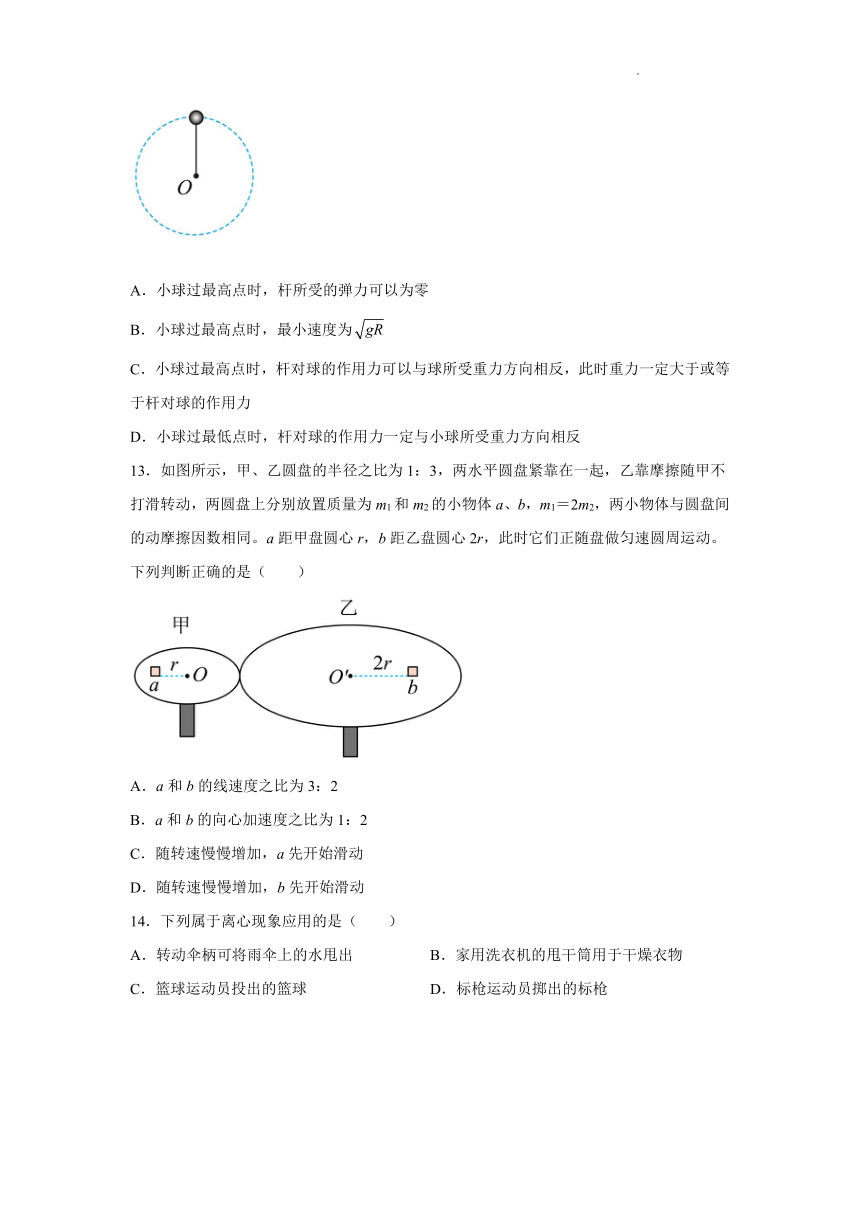
12.如图所示,某轻杆一端固定一质量为m的小球,以另一端O为圆心,使小球在竖直平面内做半径为R的圆周运动,以下说法中正确的是( )。
A.小球过最高点时,杆所受的弹力可以为零
B.小球过最高点时,最小速度为
C.小球过最高点时,杆对球的作用力可以与球所受重力方向相反,此时重力一定大于或等于杆对球的作用力
D.小球过最低点时,杆对球的作用力一定与小球所受重力方向相反
13.如图所示,甲、乙圆盘的半径之比为1:3,两水平圆盘紧靠在一起,乙靠摩擦随甲不打滑转动,两圆盘上分别放置质量为m1和m2的小物体a、b,m1=2m2,两小物体与圆盘间的动摩擦因数相同。a距甲盘圆心r,b距乙盘圆心2r,此时它们正随盘做匀速圆周运动。下列判断正确的是( )
A.a和b的线速度之比为3:2
B.a和b的向心加速度之比为1:2
C.随转速慢慢增加,a先开始滑动
D.随转速慢慢增加,b先开始滑动
14.下列属于离心现象应用的是( )
A.转动伞柄可将雨伞上的水甩出 B.家用洗衣机的甩干筒用于干燥衣物
C.篮球运动员投出的篮球 D.标枪运动员掷出的标枪
三、解答题
15.长L=0.5m的轻杆,其一端连接着一个零件A,A的质量m=2kg。现让A在竖直平面内绕O点做匀速圆周运动,如图所示。在A通过最高点时,()求下列两种情况下A对杆的作用力大小:
(1)当杆对零件无作用力时零件的速度大小;
(2)A的速率为1m/s;
(3)A的速率为4m/s。
16.如图所示,半径为R,内径很小的光滑半圆管竖直放置。两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点A时,对管壁上部的压力为3mg,b通过最高点A时,对管壁下部的压力为0.75mg,求a、b两球落地点间的距离。
17.如图所示,一根长的不可伸长轻绳,一端固定在天花板的点,另一端系一质量为的小球。现将轻绳拉直至水平位置,小球由点静止释放,小球运动到最低点点时,轻绳刚好被拉断。点下方有一倾角为的足够长的斜面,小球恰好垂直打在斜面上点。(,,)求:
(1)轻绳被拉断前瞬间的拉力大小?
(2)小球从点运动到斜面点的时间?
18.暑假里,小明去游乐场游玩,坐了一次名叫“摇头飞椅”的游艺机,如图所示,该游艺机顶上有一个半径为的“伞盖”,“伞盖”在转动过程中带动下面的悬绳转动,其示意图如图所示。“摇头飞椅”高,绳长。小明挑选了一个悬挂在“伞盖”边缘的最外侧的椅子坐下,他与座椅的总质量为。小明和椅子的转动可简化为如图所示的圆周运动。在某段时间内,“伞盖”保持在水平面内稳定旋转,绳与竖直方向夹角为。(,,)在此过程中,求:
(1)座椅受到绳子的拉力大小;
(2)小明运动的线速度大小;
所示的圆周运动。在某段时间内,“伞盖”保持在水平面内稳定旋
参考答案
1.C
【详解】
做匀速圆周运动的物体,它的周期、角速度和线速度的大小是不变的,向心加速度大小不变,方向不断变化,则向心加速度不断变化。
故选C。
2.C
【详解】
在相同的时间内甲转过60°,乙转过45°,则有
根据公式,有
可得
故选C。
3.C
【详解】
在最低点由向心力公式得
FN-mg=m
得
FN=mg+m
又由摩擦力公式有
Ff=μFN=μ(mg+m)
故选C。
4.A
【详解】
小球在光滑杆上受重力和支持力作用,两力的合力提供小球圆周运动的向心力,如图所示:
AB.由图可知,支持力
故支持力大小不变,故A正确B错误;
C.由
解得
由于RAD.设小球运动的半径为R,则有
解得
由于RAω2,故D错误。
故选A。
5.C
【详解】
AB.A、B两轮通过皮带传动,皮带不打滑,则A、B两轮边缘的线速度大小相等;B、C两轮固定在一起绕同一轴转动,则B、C两轮的角速度相等。a、b比较
va=vb
由
v=ωr
得
ωa∶ωb=rB∶rA=1∶2
b、c比较
ωb=ωc
由
v=ωr
得
vb∶vc=rB∶rC=1∶2
所以
ωa∶ωb∶ωc=1∶2∶2
va∶vb∶vc=1∶1∶2
AB错误;
C.由
知
Ta∶Tb∶Tc=2∶1∶1
选项C正确;
D.根据
a=ωv
可知
aa∶ab∶ac=1∶2∶4
D错误。
故选C。
6.C
【详解】
当滑块与转台间的摩擦力达到最大静摩擦时,滑块将要产生滑动,则
解得
则当转动半径越大时,最大角速度越小,也容易产生滑动,则当慢慢增加圆台转速,最先滑动的是C。
故选C。
7.D
【详解】
A.小球做匀速圆周运动,向心加速度大小不变,方向始终指向圆心P,时刻在变,故A错误;
B.小球做匀速圆周运动过程中,线速度大小不变,则动能保持不变,故B错误;
C.小球做匀速圆周运动的向心力大小为
故C错误;
D.设细线与竖直方向夹角为,竖直方向满足
水平方向满足
故细线上的拉力可表示为
或
故D正确。
故选D。
8.B
【详解】
硬币做圆周运动的向心力由静摩擦力提供,则:,解得,即圆盘转动的最大角速度为,故选B.
9.B
【详解】
小球到达最高点时,受重力和杆的弹力,先假设为向下的弹力,由牛顿第二定律有
解得
F=m-mg=2×N -2×10N=-4N<0
故弹力的方向与假设的方向相反,为向上的4N支持力;根据牛顿第三定律,球对杆有向下的4N压力。
故选B。
10.AC
【详解】
A.做平抛运动的物体,因为加速度是恒定的g,故每秒钟速度的改变量都等于g, 故一定相等,故A正确;
B.只有做匀速圆周运动的物体,所受合外力的方向才与速度方向垂直,故B错误;
C.做圆周运动的物体,向心加速度的方向沿半径指向圆心,而速度与半径垂直,故向心加速度的方向一定与速度方向垂直,故C正确;
D.只有做匀速圆周运动的物体,所受的合外力才等于圆周运动所需的向心力,故D错误。
故AC.
11.AB
【解析】
A、线速度相等,乙的半径小,根据公式,可知甲的向心加速度小于乙的向心加速度,故A正确;
B、周期相等,甲的半径大,乙的半径小,根据公式,甲的向心加速度大于乙的向心加速度,故B正确;
C、角速度相等,乙的线速度小,根据公式,甲的向心加速度大于乙的向心加速度,故C错误;
D、半径相等,甲的转速小,根据公式可知,甲的向心加速度小于乙的向心加速度,故D错误.
点睛:对于圆周运动的公式要采用控制变量法来理解,当半径不变时,加速度才与线速度、角速度和周期有单调性关系,而当半径也变化时,加速度与线速度、角速度和周期不具有单调性关系.
12.ACD
【详解】
A.小球过最高点时,当重力完全提供向心力时,杆对球的弹力为零,故杆所受的弹力为零,A正确;
B.小球过最高点时,当杆对小球的弹力大小与重力大小相等时,合力为零,则向心力为零,所以小球的速度为零,即为最小速度,B错误;
C.小球过最高点时,随着速度的变化,杆对球的作用力可以与球所受重力方向相反,则有
解得
故C正确;
D.小球过最低点时,圆心在最低点的上方,故合力向上,而重力是竖直向下的,故杆对球球的作用力一定竖直向上,与重力方向相反,故D正确。
故选ACD。
13.AC
【详解】
A.甲、乙两圆盘边缘上的各点线速度大小相等,由关系式
v=ωr
可得甲、乙两圆盘的角速度之比为
ω1:ω2=3:1
物体相对圆盘静止时物体的角速度等于圆盘的角速度,故m1与m2的角速度之比为3:1,则有
故A正确;
B.根据
a=ω2r
可得m1与m2的向心加速度之比为
a1:a2=(ω12 r):(ω22 2r)=9:2
故B错误;
CD.根据
μmg=mrω2
可知,m1先达到临界角速度,可知当转速增加时,m1先开始滑动,故C正确,D错误。
故选AC。
14.AB
【详解】
AB.转动伞柄可将雨伞上的水甩出以及家用洗衣机的甩干筒用于干燥衣物,都是离心现象的应用,选项AB正确;
CD.篮球运动员投出的篮球以及标枪运动员掷出的标枪,与离心运动无关,选项CD错误。
故选AB。
15.(1);(2)16N;(3)44N
【详解】
(1)当杆对零件无作用力时,通过最高点时由重力提供向心力,由牛顿第二定律得
代入数据,解得
(2)当A的速率v1=1m/s时,由于,可知杆对零件有竖直向上的支持力,由牛顿第二定律可得
代入数据,解得
(3)当A的速率v2=4m/s时,由于,可知杆对零件有竖直向下的拉力,由牛顿第二定律可得
代入数据,解得
16.3R
【详解】
设a球到达最高点时的速度为va,根据向心力公式有
mg+FNa=m
解得
设b球到达最高点时的速度为vb,根据向心力公式有
mg-FNb=m
即
解得
两小球脱离轨道后均做平抛运动,设所用时间为t,则
竖直方向
2R=gt2
水平方向
xa=vat
xb=vbt
解得
xa=4R
xb=R
故a、b两球落地点间的距离为
Δx=xa-xb=3R
17.(1);(2)0.4s
【详解】
(1)小球从到运用动能定理
在点时合力提供向心力
(2)在速度可分解为水平方向的分速度
竖直方向分速度
则根据自由落体规律公式
得
18.(1)500N;(2)7.5m/s
【详解】
(1)座椅受到绳子的拉力大小为
(2)由牛顿第二定律可知
解得小明运动的线速度大小
v=7.5m/s
一、单选题
1.对于做匀速圆周运动的物体,不断变化的物理量是( )
A.周期 B.角速度 C.向心加速度 D.线速度的大小
2.甲、乙两物体做匀速圆周运动,其质量之比为1:2,转动半径之比为1:2,在相等时间里甲转过60°,乙转过45°,则它们所受合外力之比为( )
A.1:4 B.2:3 C.4:9 D.9:16
3.一质量为m的物体,沿半径为R的向下凹的半圆形轨道滑行,如图所示,经过最低点时的速度为v,物体与轨道之间的动摩擦因数为μ,则它在最低点时受到的摩擦力为( )
A.μmg B. C. D.
4.如图所示,光滑杆偏离竖直方向的夹角为,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动。当杆角速度为ω1时,小球的旋转平面在A处,线速度为v1,球对杆的压力为N1;当杆角速度为ω2时,小球的旋转平面在B处,线速度为v2,球对杆的压力为N2,则有( )
A.N1=N2 B.N1
5.在如图所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是。若皮带不打滑,则A、B、C三轮边缘上a、b、c三点的( )
A.角速度之比为2:1:2
B.线速度大小之比为2:1:2
C.周期之比为2:1:1
D.向心加速度之比为1:2:2
6.如图所示,A、B、C 三个物体放在水平旋转圆台上,动摩擦因数均为μ,A的质量为2m,B、C 的质量均为m,A、B离轴的距离为R,C离轴的距离为2R,当慢慢增加圆台转速,最先滑动的是 ( )
A.A B.B C.C D.三个物体同时滑动
7.如图所示,质量为m的小球用长为L的细线悬于O点,细线与竖直方向的夹角为θ,使小球在水平面内以P为圆心做匀速圆周运动,角速度为ω,则下列正确的是( )
A.由于小球做匀速圆周运动,所以加速度不变
B.小球做匀速圆周运动过程中,动能不断变化
C.小球做匀速圆周运动的向心力大小为mω2L
D.细线对小球的拉力大小为mω2L
8.如图,一硬币(可视为质点)置于水平圆盘上,硬币与竖直转轴的距离为r,已知硬币与圆盘之间的动摩擦因数为(最大静摩擦力等于滑动摩擦力),重力加速度大小为g。若硬币与圆盘一起轴匀速转动,则圆盘转动的最大角速度为( )
A. B. C. D.
9.长度为0.5m的轻质细杆OA,A端有一质量为2kg的小球,以O点为圆心,在竖直平面内做圆周运动,如图所示,小球通过最高点时的速度为2m/s,取g=10m/s2,则此时轻杆OA将( )
A.受到4N的拉力 B.受到4N的压力
C.受到36N的拉力 D.受到36N的压力
二、多选题
10.下列说法正确的是
A.做平抛运动的物体,每秒钟速度的改变量一定相等
B.做圆周运动的物体,所受合外力的方向一定与速度方向垂直
C.做圆周运动的物体,向心加速度的方向一定与速度方向垂直
D.做圆周运动的物体,所受的合外力等于圆周运动所需的向心力
11.甲乙两物体都在做匀速圆周运动,在这四种情况下哪个物体的向心加速度比较大
A.线速度相等,乙的半径小,乙的向心加速度较大
B.周期相等,甲的半径大,甲的向心加速度较大
C.角速度相等,乙的线速度小,乙的向心加速度较大
D.半径相等,甲的转速小,甲的向心加速度较大
12.如图所示,某轻杆一端固定一质量为m的小球,以另一端O为圆心,使小球在竖直平面内做半径为R的圆周运动,以下说法中正确的是( )。
A.小球过最高点时,杆所受的弹力可以为零
B.小球过最高点时,最小速度为
C.小球过最高点时,杆对球的作用力可以与球所受重力方向相反,此时重力一定大于或等于杆对球的作用力
D.小球过最低点时,杆对球的作用力一定与小球所受重力方向相反
13.如图所示,甲、乙圆盘的半径之比为1:3,两水平圆盘紧靠在一起,乙靠摩擦随甲不打滑转动,两圆盘上分别放置质量为m1和m2的小物体a、b,m1=2m2,两小物体与圆盘间的动摩擦因数相同。a距甲盘圆心r,b距乙盘圆心2r,此时它们正随盘做匀速圆周运动。下列判断正确的是( )
A.a和b的线速度之比为3:2
B.a和b的向心加速度之比为1:2
C.随转速慢慢增加,a先开始滑动
D.随转速慢慢增加,b先开始滑动
14.下列属于离心现象应用的是( )
A.转动伞柄可将雨伞上的水甩出 B.家用洗衣机的甩干筒用于干燥衣物
C.篮球运动员投出的篮球 D.标枪运动员掷出的标枪
三、解答题
15.长L=0.5m的轻杆,其一端连接着一个零件A,A的质量m=2kg。现让A在竖直平面内绕O点做匀速圆周运动,如图所示。在A通过最高点时,()求下列两种情况下A对杆的作用力大小:
(1)当杆对零件无作用力时零件的速度大小;
(2)A的速率为1m/s;
(3)A的速率为4m/s。
16.如图所示,半径为R,内径很小的光滑半圆管竖直放置。两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点A时,对管壁上部的压力为3mg,b通过最高点A时,对管壁下部的压力为0.75mg,求a、b两球落地点间的距离。
17.如图所示,一根长的不可伸长轻绳,一端固定在天花板的点,另一端系一质量为的小球。现将轻绳拉直至水平位置,小球由点静止释放,小球运动到最低点点时,轻绳刚好被拉断。点下方有一倾角为的足够长的斜面,小球恰好垂直打在斜面上点。(,,)求:
(1)轻绳被拉断前瞬间的拉力大小?
(2)小球从点运动到斜面点的时间?
18.暑假里,小明去游乐场游玩,坐了一次名叫“摇头飞椅”的游艺机,如图所示,该游艺机顶上有一个半径为的“伞盖”,“伞盖”在转动过程中带动下面的悬绳转动,其示意图如图所示。“摇头飞椅”高,绳长。小明挑选了一个悬挂在“伞盖”边缘的最外侧的椅子坐下,他与座椅的总质量为。小明和椅子的转动可简化为如图所示的圆周运动。在某段时间内,“伞盖”保持在水平面内稳定旋转,绳与竖直方向夹角为。(,,)在此过程中,求:
(1)座椅受到绳子的拉力大小;
(2)小明运动的线速度大小;
所示的圆周运动。在某段时间内,“伞盖”保持在水平面内稳定旋
参考答案
1.C
【详解】
做匀速圆周运动的物体,它的周期、角速度和线速度的大小是不变的,向心加速度大小不变,方向不断变化,则向心加速度不断变化。
故选C。
2.C
【详解】
在相同的时间内甲转过60°,乙转过45°,则有
根据公式,有
可得
故选C。
3.C
【详解】
在最低点由向心力公式得
FN-mg=m
得
FN=mg+m
又由摩擦力公式有
Ff=μFN=μ(mg+m)
故选C。
4.A
【详解】
小球在光滑杆上受重力和支持力作用,两力的合力提供小球圆周运动的向心力,如图所示:
AB.由图可知,支持力
故支持力大小不变,故A正确B错误;
C.由
解得
由于RA
解得
由于RA
故选A。
5.C
【详解】
AB.A、B两轮通过皮带传动,皮带不打滑,则A、B两轮边缘的线速度大小相等;B、C两轮固定在一起绕同一轴转动,则B、C两轮的角速度相等。a、b比较
va=vb
由
v=ωr
得
ωa∶ωb=rB∶rA=1∶2
b、c比较
ωb=ωc
由
v=ωr
得
vb∶vc=rB∶rC=1∶2
所以
ωa∶ωb∶ωc=1∶2∶2
va∶vb∶vc=1∶1∶2
AB错误;
C.由
知
Ta∶Tb∶Tc=2∶1∶1
选项C正确;
D.根据
a=ωv
可知
aa∶ab∶ac=1∶2∶4
D错误。
故选C。
6.C
【详解】
当滑块与转台间的摩擦力达到最大静摩擦时,滑块将要产生滑动,则
解得
则当转动半径越大时,最大角速度越小,也容易产生滑动,则当慢慢增加圆台转速,最先滑动的是C。
故选C。
7.D
【详解】
A.小球做匀速圆周运动,向心加速度大小不变,方向始终指向圆心P,时刻在变,故A错误;
B.小球做匀速圆周运动过程中,线速度大小不变,则动能保持不变,故B错误;
C.小球做匀速圆周运动的向心力大小为
故C错误;
D.设细线与竖直方向夹角为,竖直方向满足
水平方向满足
故细线上的拉力可表示为
或
故D正确。
故选D。
8.B
【详解】
硬币做圆周运动的向心力由静摩擦力提供,则:,解得,即圆盘转动的最大角速度为,故选B.
9.B
【详解】
小球到达最高点时,受重力和杆的弹力,先假设为向下的弹力,由牛顿第二定律有
解得
F=m-mg=2×N -2×10N=-4N<0
故弹力的方向与假设的方向相反,为向上的4N支持力;根据牛顿第三定律,球对杆有向下的4N压力。
故选B。
10.AC
【详解】
A.做平抛运动的物体,因为加速度是恒定的g,故每秒钟速度的改变量都等于g, 故一定相等,故A正确;
B.只有做匀速圆周运动的物体,所受合外力的方向才与速度方向垂直,故B错误;
C.做圆周运动的物体,向心加速度的方向沿半径指向圆心,而速度与半径垂直,故向心加速度的方向一定与速度方向垂直,故C正确;
D.只有做匀速圆周运动的物体,所受的合外力才等于圆周运动所需的向心力,故D错误。
故AC.
11.AB
【解析】
A、线速度相等,乙的半径小,根据公式,可知甲的向心加速度小于乙的向心加速度,故A正确;
B、周期相等,甲的半径大,乙的半径小,根据公式,甲的向心加速度大于乙的向心加速度,故B正确;
C、角速度相等,乙的线速度小,根据公式,甲的向心加速度大于乙的向心加速度,故C错误;
D、半径相等,甲的转速小,根据公式可知,甲的向心加速度小于乙的向心加速度,故D错误.
点睛:对于圆周运动的公式要采用控制变量法来理解,当半径不变时,加速度才与线速度、角速度和周期有单调性关系,而当半径也变化时,加速度与线速度、角速度和周期不具有单调性关系.
12.ACD
【详解】
A.小球过最高点时,当重力完全提供向心力时,杆对球的弹力为零,故杆所受的弹力为零,A正确;
B.小球过最高点时,当杆对小球的弹力大小与重力大小相等时,合力为零,则向心力为零,所以小球的速度为零,即为最小速度,B错误;
C.小球过最高点时,随着速度的变化,杆对球的作用力可以与球所受重力方向相反,则有
解得
故C正确;
D.小球过最低点时,圆心在最低点的上方,故合力向上,而重力是竖直向下的,故杆对球球的作用力一定竖直向上,与重力方向相反,故D正确。
故选ACD。
13.AC
【详解】
A.甲、乙两圆盘边缘上的各点线速度大小相等,由关系式
v=ωr
可得甲、乙两圆盘的角速度之比为
ω1:ω2=3:1
物体相对圆盘静止时物体的角速度等于圆盘的角速度,故m1与m2的角速度之比为3:1,则有
故A正确;
B.根据
a=ω2r
可得m1与m2的向心加速度之比为
a1:a2=(ω12 r):(ω22 2r)=9:2
故B错误;
CD.根据
μmg=mrω2
可知,m1先达到临界角速度,可知当转速增加时,m1先开始滑动,故C正确,D错误。
故选AC。
14.AB
【详解】
AB.转动伞柄可将雨伞上的水甩出以及家用洗衣机的甩干筒用于干燥衣物,都是离心现象的应用,选项AB正确;
CD.篮球运动员投出的篮球以及标枪运动员掷出的标枪,与离心运动无关,选项CD错误。
故选AB。
15.(1);(2)16N;(3)44N
【详解】
(1)当杆对零件无作用力时,通过最高点时由重力提供向心力,由牛顿第二定律得
代入数据,解得
(2)当A的速率v1=1m/s时,由于,可知杆对零件有竖直向上的支持力,由牛顿第二定律可得
代入数据,解得
(3)当A的速率v2=4m/s时,由于,可知杆对零件有竖直向下的拉力,由牛顿第二定律可得
代入数据,解得
16.3R
【详解】
设a球到达最高点时的速度为va,根据向心力公式有
mg+FNa=m
解得
设b球到达最高点时的速度为vb,根据向心力公式有
mg-FNb=m
即
解得
两小球脱离轨道后均做平抛运动,设所用时间为t,则
竖直方向
2R=gt2
水平方向
xa=vat
xb=vbt
解得
xa=4R
xb=R
故a、b两球落地点间的距离为
Δx=xa-xb=3R
17.(1);(2)0.4s
【详解】
(1)小球从到运用动能定理
在点时合力提供向心力
(2)在速度可分解为水平方向的分速度
竖直方向分速度
则根据自由落体规律公式
得
18.(1)500N;(2)7.5m/s
【详解】
(1)座椅受到绳子的拉力大小为
(2)由牛顿第二定律可知
解得小明运动的线速度大小
v=7.5m/s
