第一章 三角形的证明 单元测试卷(含解析)
文档属性
| 名称 | 第一章 三角形的证明 单元测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 14:33:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版八年级数学下册单元测试卷
第一章 三角形的证明
一、选择题(本大题共14个小题,每题2分,共28分,在每个小题的四个选项中只有一项是符合题目要求的)
1.(2021·福建三元·八年级期中)以下列各组线段为边作三角形,不能构成直角三角形的是( )
A.,, B.3,4,5
C.1,2, D.15,36,39
2.(2021·辽宁和平·七年级期末)如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
A.①②④ B.②③④ C.①②③ D.①③④
3.(2021·山东龙口·七年级期中)在海面上有两个疑似漂浮目标. 接到消息后,A舰艇以12海里/时的速度离开港口O,向北偏西50°方向航行. 同时,B舰艇在同地以16海里/时的速度向北偏东方向行驶,如图所示,离开港口1.5小时后两船相距30海里,则B舰艇的航行方向是( )
A.北偏东60° B.北偏东50° C.北偏东40° D.北偏东30°
4.(2021·福建·武夷山市第二中学八年级期中)如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.若CD =AC,∠A =48°,则∠ACB的度数为( )
A.48° B.96° C.105° D.108°
5.(2021·山东新泰·七年级期中)在中,、、的对边分别为、、,下列条件中,能判断是直角三角形的有( )个.
①,,; ②;③;④,,.
A.1 B.2 C.3 D.4
6.(2021·辽宁大石桥·八年级期中)如图,已知等边ABC,AB=2,点D在AB上,点F在AC的延长线上,BD=CF,DE⊥BC于E,FG⊥BC于G,DF交BC于点P,则下列结论:①BE=CG;②EDP≌GFP;③∠EDP=60°;④EP=1中,一定正确的个数是( )个
A.1 B.2 C.3 D.4
7.(2021·福建·武夷山市第二中学八年级期中)如图,在△ABC中,∠C =90°,AD平分∠BAC交BC于点D,若CD=9,则点D到斜边AB的距离为( )
A.4.5 B.9 C.18 D.20
8.(2021·江苏泗阳·八年级期中)A、B、C三名同学玩“抢凳子”游戏.他们所站的位围成一个,在他们中间放一个木凳,谁先抢到凳子谁获胜,为保证游戏公平,则凳子应放的最适当的位置是在的( )
A.三边垂直平分线的交点 B.三边中线的交点
C.三个内角角平分线的交点 D.三边高的交点
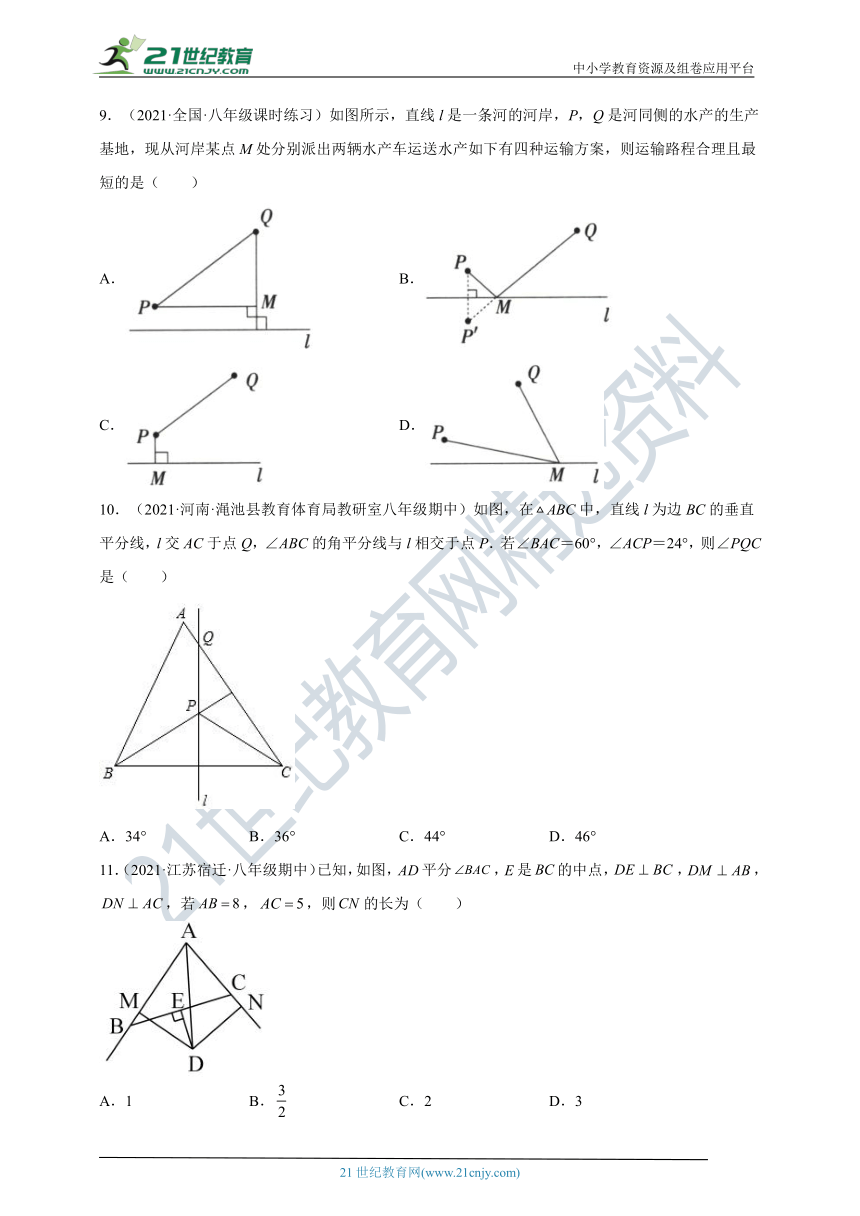
9.(2021·全国·八年级课时练习)如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
10.(2021·河南·渑池县教育体育局教研室八年级期中)如图,在ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
11.(2021·江苏宿迁·八年级期中)已知,如图,平分,是的中点,,,,若,,则的长为( )
A.1 B. C.2 D.3
12.(2021·山东阳谷·八年级期末)如图,已知△ABC中,AB=6,BC=5,AC=4,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E,连AF,则下列结论:①DE=BD+CE;②∠BFC=90°+∠ABC;③△ADE的周长为10;④S△ABF:S△ACF:S△BCF=6:4:5.正确的是( )
A.①③④ B.①②③ C.①②③④ D.②③④
13.(2021·江苏·淮安市浦东实验中学八年级期中)如图,是中的角平分线,于点,,,,则长是( )
A.5 B.6 C.7 D.8
14.(2021·福建台江·八年级期中)当题目条件出现角平分线时,我们往往可以构造等腰三角形解决问题.如图1,在中,,CD平分,,,求BC的长,解决办法:如图2,在BC边上取点E,使,连接DE,可得且是等腰三角形,所以BC的长为5,试通过构造等腰三角形解决问题:如图3,中,,,BD平分,要想求AD的长,仅需知道下列哪些线段的长(,,)( )
A.a和b B.b和c C.a和c D.a、b和c
二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上)
15.(2021·广东·西南中学八年级期中)一个三角形的三边长a,b,c满足|a﹣8|++(c﹣10)2=0,则这个三角形最长边上的高为 ___.
16.(2021·河南林州·八年级期中)如图,在中,垂直平分,交于点,交于点,,.若,则________.
17.(2021·内蒙古·呼和浩特市启东中学八年级期中)如图,∠AOB是一角度为17°的钢架,要使钢架更加牢固,需在其内部添加一些钢管:EF、FC、GH…,且OE=EF=FG=GH…,在OA、0B足够长的情况下,最多能添加这样的钢管的根数为___.
18.(2021·江苏·靖江市实验学校八年级期中)如图所示,已知△ABC的周长是15,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的面积是 ___.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.(2021·贵州清镇·八年级期中)如图,是一块草坪,已知AD=12m,CD=9m,∠ADC=90°,AB=39m,BC=36m,求这块草坪的面积.
20.(2021·浙江·绍兴市树人中学八年级期中)如图(1),△ABC中,AB=AC,∠B=2∠A.
(1)求∠A和∠B的度数;
(2)如图(2),BD是△ABC中∠ABC的平分线,写出图中与BD相等的线段,并说明理由.
21.(2021·河南·永城市教育体育局教研室八年级期末)如图,在△ABC中,AD⊥BC于点D,EF垂直平分AC,交AC于点F,交BC于点E,连接AE,且BAAE.
(1)若∠BAE30°,求∠C的度数;
(2)若△ABC的周长为18cm,AC7cm,求DC的长.
22.(2021·内蒙古·呼和浩特市启东中学八年级期中)如图,在△ABC中,BC的垂直平分线与∠BAC的平分线交于点E,过点E作EF⊥AB交AB的延长线于点F,作EG⊥AC于点G.
(1)求证:BF=CG;
(2)若AB=6,AC=8,求AF的长.
23.(2021·山东沂水·八年级期中)(问题提出)在中,,为的角平分线,探究线段,,的数量关系.
(问题解决)如图1,当,过点作,垂足为,易得;由此,如图2,当时,猜想线段,,有怎样的数量关系?给出证明.
(方法迁移)如图3,当,为的外角平分线时,探究线段,,又有怎样的数量关系?直接写出结论,不证明.
24.(2021·江苏·靖江市实验学校八年级期中)如图,△ABC中,AC=12cm,BC=5cm,AB=13cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3cm,设运动的时间为t秒.
(1)当t为何值时,CP把△ABC的周长分成相等的两部分?
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时P经过的路程?
(3)当t为何值时,△BCP为等腰三角形?(结果保留分数)
25.(2021·福建·武夷山市第二中学八年级期中)在△ABC中,AB =AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD =AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC = 90°时,那么∠DCE = 度;
(2)设∠BAC =α,∠DCE =β.
①如图2,当点D在线段CB上,∠BAC ≠ 90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图3,当点D在线段CB的延长线上,∠BAC ≠90°时,请将图3补充完整,写出此时α与β之间的数量关系并证明.
26.(2021·北京·中关村中学八年级期中)数学老师布置了一道作业题:
等边三角形ABC,过点C作直线,点D是线段BC上一点,连接AD,作AD的垂直平分线交直线于点P,在点D运动过程中,探究线段AC,DC,PC之间的数量关系.
数学小组同学们经过思考,交流了自己的想法:
小聪:利用轴对称知识,以直线为对称轴构造的轴对称图形(图2).可推得.
小明:D在运动过程中,始终不变.
小慧:通过证明三角形全等,可得到线段AC,DC,PC之间的数量关系.
(1)用等式表示线段AC,DC,PC之间的数量关系是__________.
(2)数学小组同学们解决完老师布置的作业题,进一步思考:若点D在点B左侧(如图3),再探究线段AC,DC,PC之间的数量关系,画图并证明.
(3)同学们继续思考:若点D在直线BC上运动,请直接写出线段AC,DC,PC之间的数量关系
参考答案
一、选择题
1—5ADCDD 6-10CBABA 11-14BABA
填空题
15.4.8 16.4 17.5 18.30.
三、解答题
19.【答案】216平方米
【分析】
连接AC,根据勾股定理计算AC,根据勾股定理的逆定理判定三角形ABC是直角三角形,根据面积公式计算即可.
【详解】
连接AC,∵AD=12,CD=9,∠ADC=90°,
∴AC==15,
∵AB=39,BC=36,AC=15
∴,
∴∠ACB=90°,
∴这块空地的面积为:==216(平方米),
故这块草坪的面积216平方米.
20.【答案】(1)∠A=36°,∠B=72°;(2)BD=AD=BC,理由见解析
【分析】
(1)根据等腰三角形的性质和三角形的内角和定理进行计算;
(2)结合(1)中的角的度数,又可以发现两个等腰三角形,即△ABD和△BCD.
【详解】
解:(1)∵AB=AC,∠B=2∠A,
∴∠C=∠B=2∠A,
又∵∠C+∠B+∠A=180°,
∴5∠A=180°,
∴∠A=36°,
∴∠B=72°;
(2)∵BD是△ABC中∠ABC的平分线,
∴∠ABD=∠CBD=∠A=36°,
∴∠BDC=∠A+∠ABD=∠C=72°,
∴BD=AD=BC.
21.【答案】(1)37.5°;(2)5.5cm
【分析】
(1)根据线段垂直平分线得出∠C=∠EAC,等腰三角形性质得出∠ABE=∠AEB,根据三角形外角可得∠ABE=∠AEB=2∠C,利用三角形内角和2∠C+30°+2∠C=180°即可得出答案;
(2)根据已知能推出2DE+2EC=11cm,即可得出答案.
【详解】
解:(1)∵EF垂直平分AC,
∴AE=CE,
∴∠C=∠EAC,
∵BA AE.
∴∠ABE=∠AEB,
∵∠AEB是△AEC的外角,
∴∠AEB=∠EAC+∠C=2∠C,
∴∠ABE=∠AEB=2∠C,
∵∠BAE 30°,∠AEB+∠BAE+∠ABE=180°,
∴2∠C+30°+2∠C=180°,
∴∠C=;
(2)∵AB=AE,AD⊥BE,
∴BD=DE,
∵△ABC周长18cm,AC=7cm,
∴AB+BE+EC=11cm,
即2DE+2EC=11cm,
∴DE+EC=DC=5.5cm.
22.
【答案】(1)见解析;(2)7
【分析】
(1)证明:连接BE、CE,根据线段垂直平分线的性质及角平分线的性质证明△BFE≌△CGE,即可得到结论;
(2)证明△AEF≌△AEG,推出AF=AG,得到2BF=AC-AB,求出BF,由此得到答案.
【详解】
(1)证明:连接BE、CE,
∵DE垂直平分BC,
∴BE=CE,
∵AE平分∠BAC,EF⊥AB,EG⊥AC.
∴EF=CE,∠EFB=∠CGE=90°,
∴△BFE≌△CGE,
∴BF=CG;
(2)∵AE平分∠BAC,
∴∠FAE=∠CAE,
∵∠EFB=∠CGE,AE=AE,
∴△AEF≌△AEG,
∴AF=AG,
∴AB+BF=AC-CG,
∴2BF=AC-AB=8-6=2,
∴BF=1,
∴AF=AB+BF=6+1=7.
23.【答案】(1)AB= AC(2)AB= CD-AC
【分析】
问题解决:在线段AB上截取AM=AC,连接DM,由角平分线定义和全等三角形的判定证明△AMD≌△ACD,进而证得DM=CD,∠AMD=∠ACB,结合三角形外角性质可证得∠B=∠BDM,进而证得BM=DM=CD即可解答;
方法迁移:在BA的延长线上截取AN=AC,连接DN,证明△AND≌△ACD,进而证得DN=CD,∠AND=∠ACD,结合等角的补角相等和三角形外角性质可证得∠B=∠BDN,进而证得BN=DN即可解答.
【详解】
解:问题解决:AB= AC+CD,
证明:如图,在线段AB上截取AM=AC,连接DM,
∵AD为∠BAC的角平分线,
∴∠MAD=∠CAD,又AD=AD,
∴△AMD≌△ACD(SAS),
∴DM=CD,∠AMD=∠ACB,
∵∠AMD=∠B+∠BDM,∠ACB=2∠B,
∴∠B=∠BDM,
∴BM=DM=CD,
∴AB=AM+BM=AC+CD;
方法迁移:AB= CD-AC.
证明:如图,在BA的延长线上截取AN=AC,连接DN,
∵AD为∠BAC的外角平分线,
∴∠NAD=∠CAD,又AD=AD,
∴△AND≌△ACD(SAS),
∴DN=CD,∠AND=∠ACD,
∵∠ACB+∠ACD=180°,∠DNE+∠AND=180°,
∴∠ACB=∠DNE,
∵∠DNE=∠B+∠BDN,∠ACB=2∠B,
∴∠B=∠BDN,
∴BN=DN=CD,
∴AB=BN-AN=CD-AC.
24.【答案】(1);(2)(3)或或或
【分析】
(1)根据题意当CP把△ABC的周长分成相等的两部分时,点在上,进而根据时间等于路程除以速度即可求得;
(2)根据题意当点运动到的中点时,CP把△ABC的面积分成相等的两部分,进而列出一元一次方程,解方程求解即可;
(3)先证明△ABC是直角三角形,分三种情况讨论,①当时,点在上时,和当点在上时;②当时,此时点在上,③当时,此时是的垂直平分线与的交点,如图,过点作于点,进而求得
【详解】
(1)△ABC的周长为,
当CP把△ABC的周长分成相等的两部分时,点在上,
此时
即
解得
(2)根据题意,当点运动到的中点时,CP把△ABC的面积分成相等的两部分,
此时
解得
(3) AC=12cm,BC=5cm,AB=13cm,
△ABC是直角三角形
①当时,如图,当在的位置,即点在上时,,
即
解得
当点在上时,如图,过点作,
则
在中,
,
则
解得
②当时,此时点在上,
则
即
解得
③当时,此时是的垂直平分线与的交点,如图,过点作,于点
,
是的中点,由(2)可知
综上所述,当或或或时,△BCP为等腰三角形
25.【答案】(1)90°;(2)①α+β=180°;②α=β.
【分析】
(1)根据∠DAE=∠BAC,得到∠BAD=∠CAE,推出△ABD≌△ACE,根据全等三角形的性质得到∠ACE=∠ABC=45°,由此得到结论;
(2)①由∠BAC=∠DAE,得到∠BAD=∠CAE,推出△ABD≌△ACE,根据全等三角形的性质得到∠B=∠ACE,于是得到∠B+∠ACB=∠ACE+∠ACB,证得∠B+∠ACB=∠DCE=β,即可得到结论;
②由∠DAE=∠BAC,得到∠DAB=∠EAC,推出△ABD≌△ACE,根据全等三角形的性质得到∠ADB=∠AEC,根据三角形内角和定理得到∠ADE+∠AED+α=180°,∠CDE+∠CED+β=180°以及∠CED=∠AEC+∠AED,由此得到α=β.
【详解】
解:(1)∵AB =AC,∠BAC = 90°,
∴∠ABC=∠ACB=45°,
∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD与△ACE中,,
∴△ABD≌△ACE,
∴∠ACE=∠ABC=45°,
∴∠DCE =90°,
故答案为:90°;
(2)①∵∠DAE=∠BAC,
∴∠BAD+∠DAC=α,∠DAC+∠CAE=α,
∴∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),∴∠ACE=∠B,
∵∠B+∠ACB=180°﹣α,∴∠DCE=∠ACE+∠ACB=180°﹣α=β,
∴α+β=180°;
(3)作出图形,
∵∠BAD+∠BAE=α,∠BAE+∠CAE=α,
∴∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),
∴∠AEC=∠ADB,
∵∠ADE+∠AED+α=180°,∠CDE+∠CED+β=180°,∠CED=∠AEC+∠AED,
∴α=β.
26.【答案】(1);(2);(3)
【分析】
(1)以直线为对称轴构造的轴对称图形,设交于点,证明是等边三角形,进而证明,可得,根据等边三角形的性质可得,进而可得;
(2)以直线为对称轴构造的轴对称图形,同理可得,是等边三角形,进而证明,可得,根据等边三角形的性质可得,;
(3)当在点右侧时,以直线为对称轴构造的轴对称图形,设,进而证明,即可证明,进而可得
【详解】
解:(1)如图,以直线为对称轴构造的轴对称图形,设交于点,
是等边三角形
,
,
三点共线
与关于对称,
,
是的垂直平分线上的一点
又
是等边三角形
在与中,
即
故答案为:
(2)如图,以直线为对称轴构造的轴对称图形,
由(1)可得在同一直线上,
是等边三角形
在与中
(3)如图,当在点右侧时,以直线为对称轴构造的轴对称图形,
由(1)可得在同一直线上
,,
设,
又
是等边三角形
,
即
在与中
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版八年级数学下册单元测试卷
第一章 三角形的证明
一、选择题(本大题共14个小题,每题2分,共28分,在每个小题的四个选项中只有一项是符合题目要求的)
1.(2021·福建三元·八年级期中)以下列各组线段为边作三角形,不能构成直角三角形的是( )
A.,, B.3,4,5
C.1,2, D.15,36,39
2.(2021·辽宁和平·七年级期末)如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
A.①②④ B.②③④ C.①②③ D.①③④
3.(2021·山东龙口·七年级期中)在海面上有两个疑似漂浮目标. 接到消息后,A舰艇以12海里/时的速度离开港口O,向北偏西50°方向航行. 同时,B舰艇在同地以16海里/时的速度向北偏东方向行驶,如图所示,离开港口1.5小时后两船相距30海里,则B舰艇的航行方向是( )
A.北偏东60° B.北偏东50° C.北偏东40° D.北偏东30°
4.(2021·福建·武夷山市第二中学八年级期中)如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.若CD =AC,∠A =48°,则∠ACB的度数为( )
A.48° B.96° C.105° D.108°
5.(2021·山东新泰·七年级期中)在中,、、的对边分别为、、,下列条件中,能判断是直角三角形的有( )个.
①,,; ②;③;④,,.
A.1 B.2 C.3 D.4
6.(2021·辽宁大石桥·八年级期中)如图,已知等边ABC,AB=2,点D在AB上,点F在AC的延长线上,BD=CF,DE⊥BC于E,FG⊥BC于G,DF交BC于点P,则下列结论:①BE=CG;②EDP≌GFP;③∠EDP=60°;④EP=1中,一定正确的个数是( )个
A.1 B.2 C.3 D.4
7.(2021·福建·武夷山市第二中学八年级期中)如图,在△ABC中,∠C =90°,AD平分∠BAC交BC于点D,若CD=9,则点D到斜边AB的距离为( )
A.4.5 B.9 C.18 D.20
8.(2021·江苏泗阳·八年级期中)A、B、C三名同学玩“抢凳子”游戏.他们所站的位围成一个,在他们中间放一个木凳,谁先抢到凳子谁获胜,为保证游戏公平,则凳子应放的最适当的位置是在的( )
A.三边垂直平分线的交点 B.三边中线的交点
C.三个内角角平分线的交点 D.三边高的交点
9.(2021·全国·八年级课时练习)如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
10.(2021·河南·渑池县教育体育局教研室八年级期中)如图,在ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
11.(2021·江苏宿迁·八年级期中)已知,如图,平分,是的中点,,,,若,,则的长为( )
A.1 B. C.2 D.3
12.(2021·山东阳谷·八年级期末)如图,已知△ABC中,AB=6,BC=5,AC=4,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E,连AF,则下列结论:①DE=BD+CE;②∠BFC=90°+∠ABC;③△ADE的周长为10;④S△ABF:S△ACF:S△BCF=6:4:5.正确的是( )
A.①③④ B.①②③ C.①②③④ D.②③④
13.(2021·江苏·淮安市浦东实验中学八年级期中)如图,是中的角平分线,于点,,,,则长是( )
A.5 B.6 C.7 D.8
14.(2021·福建台江·八年级期中)当题目条件出现角平分线时,我们往往可以构造等腰三角形解决问题.如图1,在中,,CD平分,,,求BC的长,解决办法:如图2,在BC边上取点E,使,连接DE,可得且是等腰三角形,所以BC的长为5,试通过构造等腰三角形解决问题:如图3,中,,,BD平分,要想求AD的长,仅需知道下列哪些线段的长(,,)( )
A.a和b B.b和c C.a和c D.a、b和c
二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上)
15.(2021·广东·西南中学八年级期中)一个三角形的三边长a,b,c满足|a﹣8|++(c﹣10)2=0,则这个三角形最长边上的高为 ___.
16.(2021·河南林州·八年级期中)如图,在中,垂直平分,交于点,交于点,,.若,则________.
17.(2021·内蒙古·呼和浩特市启东中学八年级期中)如图,∠AOB是一角度为17°的钢架,要使钢架更加牢固,需在其内部添加一些钢管:EF、FC、GH…,且OE=EF=FG=GH…,在OA、0B足够长的情况下,最多能添加这样的钢管的根数为___.
18.(2021·江苏·靖江市实验学校八年级期中)如图所示,已知△ABC的周长是15,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的面积是 ___.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.(2021·贵州清镇·八年级期中)如图,是一块草坪,已知AD=12m,CD=9m,∠ADC=90°,AB=39m,BC=36m,求这块草坪的面积.
20.(2021·浙江·绍兴市树人中学八年级期中)如图(1),△ABC中,AB=AC,∠B=2∠A.
(1)求∠A和∠B的度数;
(2)如图(2),BD是△ABC中∠ABC的平分线,写出图中与BD相等的线段,并说明理由.
21.(2021·河南·永城市教育体育局教研室八年级期末)如图,在△ABC中,AD⊥BC于点D,EF垂直平分AC,交AC于点F,交BC于点E,连接AE,且BAAE.
(1)若∠BAE30°,求∠C的度数;
(2)若△ABC的周长为18cm,AC7cm,求DC的长.
22.(2021·内蒙古·呼和浩特市启东中学八年级期中)如图,在△ABC中,BC的垂直平分线与∠BAC的平分线交于点E,过点E作EF⊥AB交AB的延长线于点F,作EG⊥AC于点G.
(1)求证:BF=CG;
(2)若AB=6,AC=8,求AF的长.
23.(2021·山东沂水·八年级期中)(问题提出)在中,,为的角平分线,探究线段,,的数量关系.
(问题解决)如图1,当,过点作,垂足为,易得;由此,如图2,当时,猜想线段,,有怎样的数量关系?给出证明.
(方法迁移)如图3,当,为的外角平分线时,探究线段,,又有怎样的数量关系?直接写出结论,不证明.
24.(2021·江苏·靖江市实验学校八年级期中)如图,△ABC中,AC=12cm,BC=5cm,AB=13cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3cm,设运动的时间为t秒.
(1)当t为何值时,CP把△ABC的周长分成相等的两部分?
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时P经过的路程?
(3)当t为何值时,△BCP为等腰三角形?(结果保留分数)
25.(2021·福建·武夷山市第二中学八年级期中)在△ABC中,AB =AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD =AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC = 90°时,那么∠DCE = 度;
(2)设∠BAC =α,∠DCE =β.
①如图2,当点D在线段CB上,∠BAC ≠ 90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图3,当点D在线段CB的延长线上,∠BAC ≠90°时,请将图3补充完整,写出此时α与β之间的数量关系并证明.
26.(2021·北京·中关村中学八年级期中)数学老师布置了一道作业题:
等边三角形ABC,过点C作直线,点D是线段BC上一点,连接AD,作AD的垂直平分线交直线于点P,在点D运动过程中,探究线段AC,DC,PC之间的数量关系.
数学小组同学们经过思考,交流了自己的想法:
小聪:利用轴对称知识,以直线为对称轴构造的轴对称图形(图2).可推得.
小明:D在运动过程中,始终不变.
小慧:通过证明三角形全等,可得到线段AC,DC,PC之间的数量关系.
(1)用等式表示线段AC,DC,PC之间的数量关系是__________.
(2)数学小组同学们解决完老师布置的作业题,进一步思考:若点D在点B左侧(如图3),再探究线段AC,DC,PC之间的数量关系,画图并证明.
(3)同学们继续思考:若点D在直线BC上运动,请直接写出线段AC,DC,PC之间的数量关系
参考答案
一、选择题
1—5ADCDD 6-10CBABA 11-14BABA
填空题
15.4.8 16.4 17.5 18.30.
三、解答题
19.【答案】216平方米
【分析】
连接AC,根据勾股定理计算AC,根据勾股定理的逆定理判定三角形ABC是直角三角形,根据面积公式计算即可.
【详解】
连接AC,∵AD=12,CD=9,∠ADC=90°,
∴AC==15,
∵AB=39,BC=36,AC=15
∴,
∴∠ACB=90°,
∴这块空地的面积为:==216(平方米),
故这块草坪的面积216平方米.
20.【答案】(1)∠A=36°,∠B=72°;(2)BD=AD=BC,理由见解析
【分析】
(1)根据等腰三角形的性质和三角形的内角和定理进行计算;
(2)结合(1)中的角的度数,又可以发现两个等腰三角形,即△ABD和△BCD.
【详解】
解:(1)∵AB=AC,∠B=2∠A,
∴∠C=∠B=2∠A,
又∵∠C+∠B+∠A=180°,
∴5∠A=180°,
∴∠A=36°,
∴∠B=72°;
(2)∵BD是△ABC中∠ABC的平分线,
∴∠ABD=∠CBD=∠A=36°,
∴∠BDC=∠A+∠ABD=∠C=72°,
∴BD=AD=BC.
21.【答案】(1)37.5°;(2)5.5cm
【分析】
(1)根据线段垂直平分线得出∠C=∠EAC,等腰三角形性质得出∠ABE=∠AEB,根据三角形外角可得∠ABE=∠AEB=2∠C,利用三角形内角和2∠C+30°+2∠C=180°即可得出答案;
(2)根据已知能推出2DE+2EC=11cm,即可得出答案.
【详解】
解:(1)∵EF垂直平分AC,
∴AE=CE,
∴∠C=∠EAC,
∵BA AE.
∴∠ABE=∠AEB,
∵∠AEB是△AEC的外角,
∴∠AEB=∠EAC+∠C=2∠C,
∴∠ABE=∠AEB=2∠C,
∵∠BAE 30°,∠AEB+∠BAE+∠ABE=180°,
∴2∠C+30°+2∠C=180°,
∴∠C=;
(2)∵AB=AE,AD⊥BE,
∴BD=DE,
∵△ABC周长18cm,AC=7cm,
∴AB+BE+EC=11cm,
即2DE+2EC=11cm,
∴DE+EC=DC=5.5cm.
22.
【答案】(1)见解析;(2)7
【分析】
(1)证明:连接BE、CE,根据线段垂直平分线的性质及角平分线的性质证明△BFE≌△CGE,即可得到结论;
(2)证明△AEF≌△AEG,推出AF=AG,得到2BF=AC-AB,求出BF,由此得到答案.
【详解】
(1)证明:连接BE、CE,
∵DE垂直平分BC,
∴BE=CE,
∵AE平分∠BAC,EF⊥AB,EG⊥AC.
∴EF=CE,∠EFB=∠CGE=90°,
∴△BFE≌△CGE,
∴BF=CG;
(2)∵AE平分∠BAC,
∴∠FAE=∠CAE,
∵∠EFB=∠CGE,AE=AE,
∴△AEF≌△AEG,
∴AF=AG,
∴AB+BF=AC-CG,
∴2BF=AC-AB=8-6=2,
∴BF=1,
∴AF=AB+BF=6+1=7.
23.【答案】(1)AB= AC(2)AB= CD-AC
【分析】
问题解决:在线段AB上截取AM=AC,连接DM,由角平分线定义和全等三角形的判定证明△AMD≌△ACD,进而证得DM=CD,∠AMD=∠ACB,结合三角形外角性质可证得∠B=∠BDM,进而证得BM=DM=CD即可解答;
方法迁移:在BA的延长线上截取AN=AC,连接DN,证明△AND≌△ACD,进而证得DN=CD,∠AND=∠ACD,结合等角的补角相等和三角形外角性质可证得∠B=∠BDN,进而证得BN=DN即可解答.
【详解】
解:问题解决:AB= AC+CD,
证明:如图,在线段AB上截取AM=AC,连接DM,
∵AD为∠BAC的角平分线,
∴∠MAD=∠CAD,又AD=AD,
∴△AMD≌△ACD(SAS),
∴DM=CD,∠AMD=∠ACB,
∵∠AMD=∠B+∠BDM,∠ACB=2∠B,
∴∠B=∠BDM,
∴BM=DM=CD,
∴AB=AM+BM=AC+CD;
方法迁移:AB= CD-AC.
证明:如图,在BA的延长线上截取AN=AC,连接DN,
∵AD为∠BAC的外角平分线,
∴∠NAD=∠CAD,又AD=AD,
∴△AND≌△ACD(SAS),
∴DN=CD,∠AND=∠ACD,
∵∠ACB+∠ACD=180°,∠DNE+∠AND=180°,
∴∠ACB=∠DNE,
∵∠DNE=∠B+∠BDN,∠ACB=2∠B,
∴∠B=∠BDN,
∴BN=DN=CD,
∴AB=BN-AN=CD-AC.
24.【答案】(1);(2)(3)或或或
【分析】
(1)根据题意当CP把△ABC的周长分成相等的两部分时,点在上,进而根据时间等于路程除以速度即可求得;
(2)根据题意当点运动到的中点时,CP把△ABC的面积分成相等的两部分,进而列出一元一次方程,解方程求解即可;
(3)先证明△ABC是直角三角形,分三种情况讨论,①当时,点在上时,和当点在上时;②当时,此时点在上,③当时,此时是的垂直平分线与的交点,如图,过点作于点,进而求得
【详解】
(1)△ABC的周长为,
当CP把△ABC的周长分成相等的两部分时,点在上,
此时
即
解得
(2)根据题意,当点运动到的中点时,CP把△ABC的面积分成相等的两部分,
此时
解得
(3) AC=12cm,BC=5cm,AB=13cm,
△ABC是直角三角形
①当时,如图,当在的位置,即点在上时,,
即
解得
当点在上时,如图,过点作,
则
在中,
,
则
解得
②当时,此时点在上,
则
即
解得
③当时,此时是的垂直平分线与的交点,如图,过点作,于点
,
是的中点,由(2)可知
综上所述,当或或或时,△BCP为等腰三角形
25.【答案】(1)90°;(2)①α+β=180°;②α=β.
【分析】
(1)根据∠DAE=∠BAC,得到∠BAD=∠CAE,推出△ABD≌△ACE,根据全等三角形的性质得到∠ACE=∠ABC=45°,由此得到结论;
(2)①由∠BAC=∠DAE,得到∠BAD=∠CAE,推出△ABD≌△ACE,根据全等三角形的性质得到∠B=∠ACE,于是得到∠B+∠ACB=∠ACE+∠ACB,证得∠B+∠ACB=∠DCE=β,即可得到结论;
②由∠DAE=∠BAC,得到∠DAB=∠EAC,推出△ABD≌△ACE,根据全等三角形的性质得到∠ADB=∠AEC,根据三角形内角和定理得到∠ADE+∠AED+α=180°,∠CDE+∠CED+β=180°以及∠CED=∠AEC+∠AED,由此得到α=β.
【详解】
解:(1)∵AB =AC,∠BAC = 90°,
∴∠ABC=∠ACB=45°,
∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD与△ACE中,,
∴△ABD≌△ACE,
∴∠ACE=∠ABC=45°,
∴∠DCE =90°,
故答案为:90°;
(2)①∵∠DAE=∠BAC,
∴∠BAD+∠DAC=α,∠DAC+∠CAE=α,
∴∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),∴∠ACE=∠B,
∵∠B+∠ACB=180°﹣α,∴∠DCE=∠ACE+∠ACB=180°﹣α=β,
∴α+β=180°;
(3)作出图形,
∵∠BAD+∠BAE=α,∠BAE+∠CAE=α,
∴∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),
∴∠AEC=∠ADB,
∵∠ADE+∠AED+α=180°,∠CDE+∠CED+β=180°,∠CED=∠AEC+∠AED,
∴α=β.
26.【答案】(1);(2);(3)
【分析】
(1)以直线为对称轴构造的轴对称图形,设交于点,证明是等边三角形,进而证明,可得,根据等边三角形的性质可得,进而可得;
(2)以直线为对称轴构造的轴对称图形,同理可得,是等边三角形,进而证明,可得,根据等边三角形的性质可得,;
(3)当在点右侧时,以直线为对称轴构造的轴对称图形,设,进而证明,即可证明,进而可得
【详解】
解:(1)如图,以直线为对称轴构造的轴对称图形,设交于点,
是等边三角形
,
,
三点共线
与关于对称,
,
是的垂直平分线上的一点
又
是等边三角形
在与中,
即
故答案为:
(2)如图,以直线为对称轴构造的轴对称图形,
由(1)可得在同一直线上,
是等边三角形
在与中
(3)如图,当在点右侧时,以直线为对称轴构造的轴对称图形,
由(1)可得在同一直线上
,,
设,
又
是等边三角形
,
即
在与中
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
