2021-2022学年浙江省杭州市西湖区十三中八年级(下)开学数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年浙江省杭州市西湖区十三中八年级(下)开学数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 893.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 14:59:42 | ||
图片预览



文档简介
2021-2022学年浙江省杭州市西湖区十三中八年级(下)开学数学试卷
一、选择题
1.下列冬奥会会徽中,属于轴对称图形的是( )
A. B.
C. D.
2.有下列长度的三条线段,其中能组成三角形的是( )
A.4,5,9 B.2.5,6.5,10 C.3,4,5 D.5,12,17
3.点P(a,1)在第一象限,则a的取值范围是( )
A.a>0 B.a≥0 C.a<0 D.a≤0
4.下列各式中,是二次根式有( )
①;②;③;④;⑤;⑥.
A.2个 B.3个 C.4个 D.5个
5.若x>y,则下列式子中错误的是( )
A.x﹣2>y﹣2 B.x+2>y+2 C.﹣2x>﹣2y D.>
6.一次函数y=kx﹣2k的大致图象是( )
A. B.
C. D.
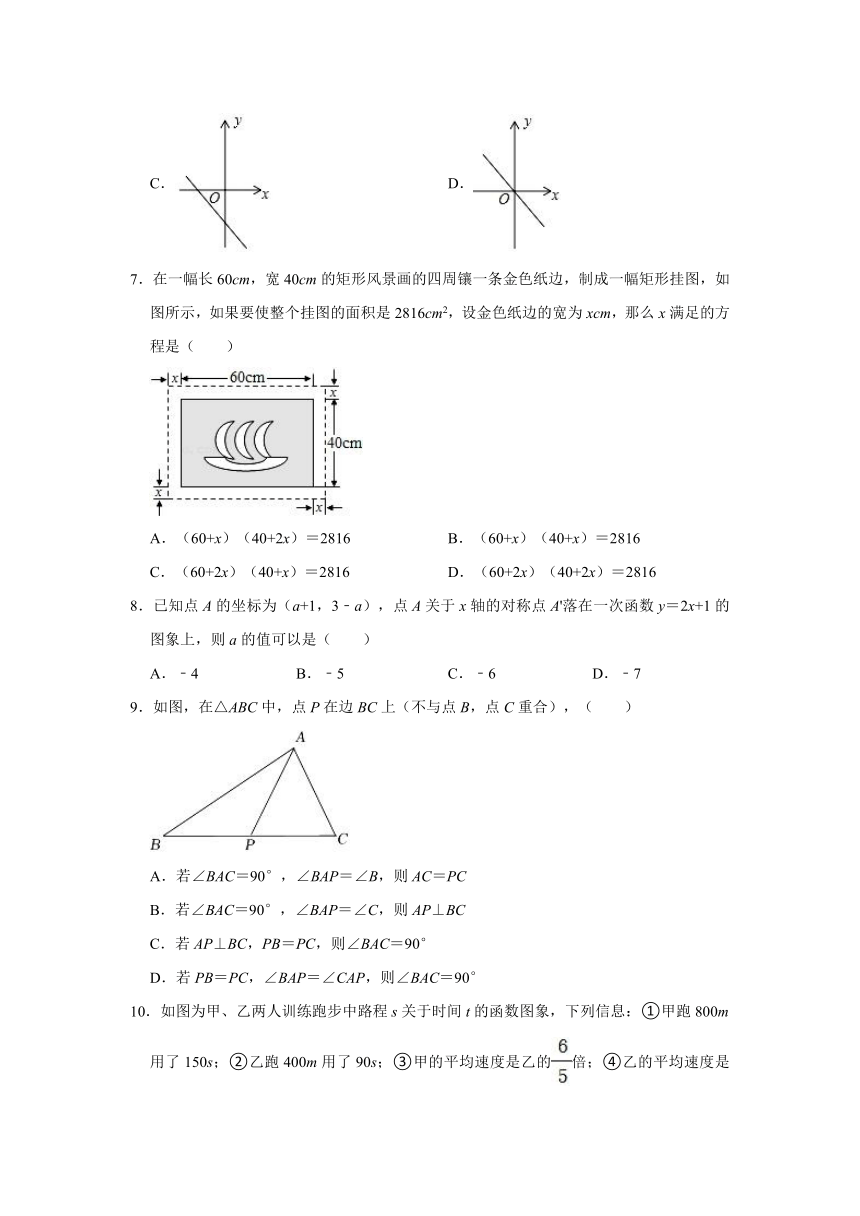
7.在一幅长60cm,宽40cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是2816cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.(60+x)(40+2x)=2816 B.(60+x)(40+x)=2816
C.(60+2x)(40+x)=2816 D.(60+2x)(40+2x)=2816
8.已知点A的坐标为(a+1,3﹣a),点A关于x轴的对称点A'落在一次函数y=2x+1的图象上,则a的值可以是( )
A.﹣4 B.﹣5 C.﹣6 D.﹣7
9.如图,在△ABC中,点P在边BC上(不与点B,点C重合),( )
A.若∠BAC=90°,∠BAP=∠B,则AC=PC
B.若∠BAC=90°,∠BAP=∠C,则AP⊥BC
C.若AP⊥BC,PB=PC,则∠BAC=90°
D.若PB=PC,∠BAP=∠CAP,则∠BAC=90°
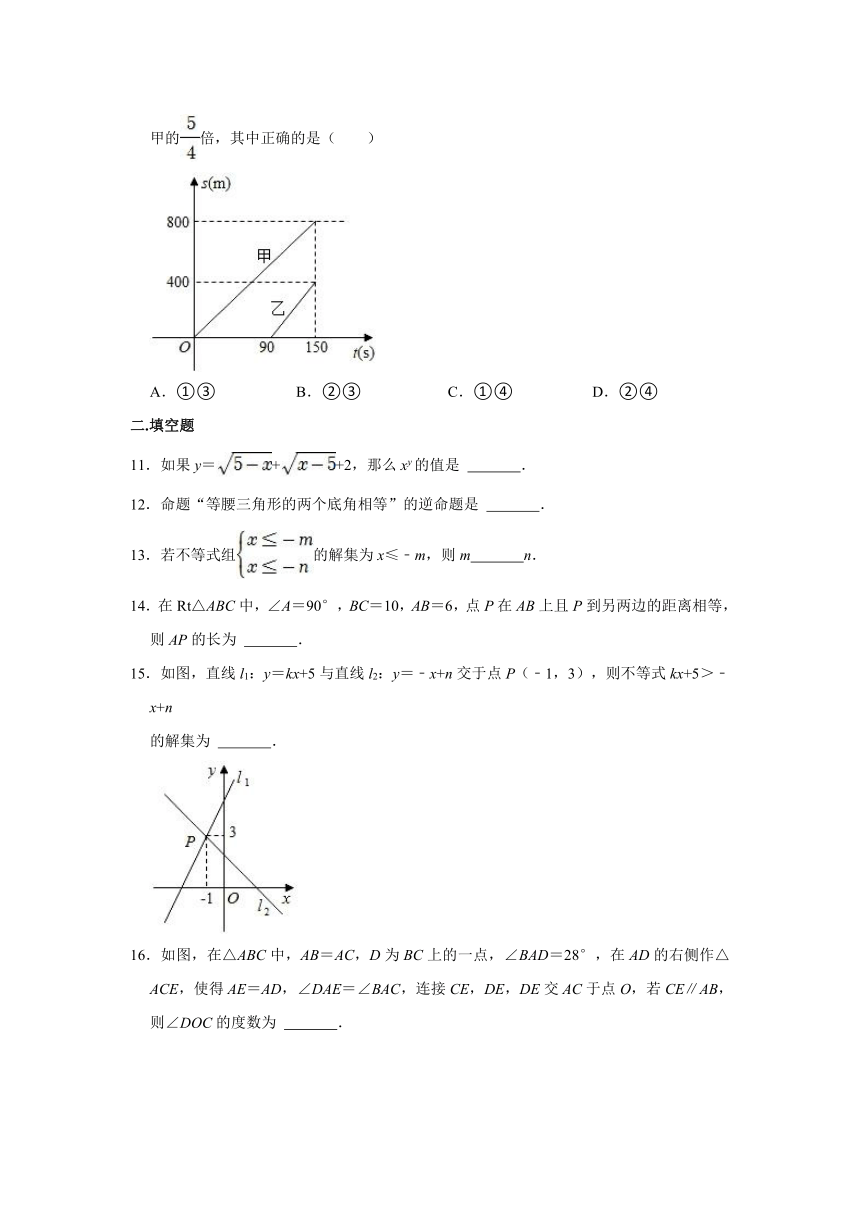
10.如图为甲、乙两人训练跑步中路程s关于时间t的函数图象,下列信息:①甲跑800m用了150s;②乙跑400m用了90s;③甲的平均速度是乙的倍;④乙的平均速度是甲的倍,其中正确的是( )
A.①③ B.②③ C.①④ D.②④
二.填空题
11.如果y=++2,那么xy的值是 .
12.命题“等腰三角形的两个底角相等”的逆命题是 .
13.若不等式组的解集为x≤﹣m,则m n.
14.在Rt△ABC中,∠A=90°,BC=10,AB=6,点P在AB上且P到另两边的距离相等,则AP的长为 .
15.如图,直线l1:y=kx+5与直线l2:y=﹣x+n交于点P(﹣1,3),则不等式kx+5>﹣x+n
的解集为 .
16.如图,在△ABC中,AB=AC,D为BC上的一点,∠BAD=28°,在AD的右侧作△ACE,使得AE=AD,∠DAE=∠BAC,连接CE,DE,DE交AC于点O,若CE∥AB,则∠DOC的度数为 .
三.解答题
17.计算:
(1);
(2).
18.(1);
(2)+2=.
19.小聪去购买笔记本和钢笔共30件,每本笔记本2元,每支钢笔5元,若购买的钢笔数量不少于笔记本的数量.
(1)小聪至多能买几本笔记本?
(2)若小聪只带了130元钱,此时他至少要买几本笔记本?
20.已知一次函数y=kx+b的图象过(1,6)和(﹣1,2).
(1)求一次函数y=kx+b的关系式;
(2)求一次函数y=kx+b的图象与坐标轴围成的三角形的面积.
21.如图,在△ABC中,AB=AC,D为CA延长线上一点,且DE⊥BC交AB于点F.
(1)求证:△ADF是等腰三角形;
(2)若AC=10,BE=3,F为AB中点,求DF的长.
22.如图,在△ABC中,AB=AC,点D在AC边上(不与点A,点C重合),连接BD,BD=AB.
(1)设∠C=α,∠ABD=β.
①当α=50°时,求β.
②直接写出β与α之间的等量关系及α的取值范围.
(2)若AB=5,BC=6,求AD的长.
23.设函数y1=ax+b,y2=bx+a(a,b为常数,ab≠0且a≠b),函数y和y的图象的交点为点P.
(1)求证:点P在y轴的右侧.
(2)已知点P在第一象限,函数y的值随x的增大而增大.
①当x=2时,y1﹣y2=2,求a的取值范围.
②若点P的坐标是(1,1),且a>b,求证:当x=2时,y1﹣y2<﹣.
参考答案
一、选择题
1.下列冬奥会会徽中,属于轴对称图形的是( )
A. B.
C. D.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
解:选项A、B、C不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:D.
2.有下列长度的三条线段,其中能组成三角形的是( )
A.4,5,9 B.2.5,6.5,10 C.3,4,5 D.5,12,17
【分析】三角形的三条边必须满足:任意两边之和>第三边,任意两边之差<第三边.
解:A、4+5=9,故不能组成三角形,不符合题意;
B、2.5+6.5<10,不能组成三角形,不符合题意;
C、4+3>5,能组成三角形,符合题意;
D、5+12=17,不能组成三角形,不符合题意;
故选:C.
3.点P(a,1)在第一象限,则a的取值范围是( )
A.a>0 B.a≥0 C.a<0 D.a≤0
【分析】由第一象限内点的坐标符号特点求解即可.
解:∵点P(a,1)在第一象限,
∴a>0,
故选:A.
4.下列各式中,是二次根式有( )
①;②;③;④;⑤;⑥.
A.2个 B.3个 C.4个 D.5个
【分析】根据二次根式的概念进行分析判断.
解:①是二次根式,
②没有意义,不是二次根式,
③是三次根式,不是二次根式,
④没有意义,不是二次根式,
⑤是二次根式,
⑥是二次根式,
∴①⑤⑥是二次根式,共3个,
故选:B.
5.若x>y,则下列式子中错误的是( )
A.x﹣2>y﹣2 B.x+2>y+2 C.﹣2x>﹣2y D.>
【分析】A:不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变,据此判断即可.
B:不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变,据此判断即可.
C:不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变,据此判断即可.
D:不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变,据此判断即可.
解:∵x>y,
∴x﹣2>y﹣2,
∴选项A正确;
∵x>y,
∴x+2>y+2,
∴选项B正确;
∵x>y,
∴﹣2x<﹣2y,
∴选项C不正确;
∵x>y,
∴,
∴选项D正确.
故选:C.
6.一次函数y=kx﹣2k的大致图象是( )
A. B.
C. D.
【分析】一次函数解析式为y=kx﹣2k,易得其图象与x轴的交点为(2,0),分析选项可得答案.
解:函数的解析式为y=kx﹣2k
即函数图象与x轴的交点为(2,0),
分析可得,B选项符合题意.
故选:B.
7.在一幅长60cm,宽40cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是2816cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.(60+x)(40+2x)=2816 B.(60+x)(40+x)=2816
C.(60+2x)(40+x)=2816 D.(60+2x)(40+2x)=2816
【分析】根据题意可知:矩形挂图的长为(60+2x)cm,宽为(40+2x)cm;则运用面积公式列方程即可.
解:挂图长为(60+2x)cm,宽为(40+2x)cm,
所以根据矩形的面积公式可得:(60+2x)(40+2x)=2816.
故选:D.
8.已知点A的坐标为(a+1,3﹣a),点A关于x轴的对称点A'落在一次函数y=2x+1的图象上,则a的值可以是( )
A.﹣4 B.﹣5 C.﹣6 D.﹣7
【分析】根据对称的性质求出点A′的坐标,再把点A′的坐标代入y=2x+1,即可求出a.
解:∵点A的坐标为(a+1,3﹣a),
∴点A关于x轴的对称点A'的坐标是(a+1,﹣3+a),
∵点A′在一次函数y=2x+1的图象上,
∴﹣3+a=2(a+1)+1,
解得:a=﹣6,
故选:C.
9.如图,在△ABC中,点P在边BC上(不与点B,点C重合),( )
A.若∠BAC=90°,∠BAP=∠B,则AC=PC
B.若∠BAC=90°,∠BAP=∠C,则AP⊥BC
C.若AP⊥BC,PB=PC,则∠BAC=90°
D.若PB=PC,∠BAP=∠CAP,则∠BAC=90°
【分析】根据直角三角形的性质逐项判定可求解.
解:A.∵∠BAC=90°,
∴∠BAP+∠CAP=∠B+∠C=90°,
∵∠BAP=∠B,
∴∠CAP=∠C,
∴AP=PC,
只有当∠B=30°时,AC=PC,故错误;
B.∵∠BAC=90°,
∴∠BAP+∠CAP=90°,
∵∠BAP=∠C,
∴∠C+∠CAP=90°,
∴∠APC=180°﹣(∠C+∠CAP)=90°,
即AP⊥BC,故正确;
C.∵AP⊥BC,PB=PC,
∴AP垂直平分BC,
而∠BAC不一定等于90°,故错误;
D.根据PB=PC,∠BAP=∠CAP,无法证明∠BAC=90°,故错误,
故选:B.
10.如图为甲、乙两人训练跑步中路程s关于时间t的函数图象,下列信息:①甲跑800m用了150s;②乙跑400m用了90s;③甲的平均速度是乙的倍;④乙的平均速度是甲的倍,其中正确的是( )
A.①③ B.②③ C.①④ D.②④
【分析】根据函数图象中的数据,可以直接判断①、②,再根据图象中的数据,计算出甲、乙的速度,然后即可判断③、④.
解:由图象可得,
甲跑800m用了150s,故①正确;
乙跑400m用了150﹣90=60(s),故②错误;
甲的平均速度是800÷150=(m/s),乙的平均速度是400÷60=(m/s),
则甲的平均速度是乙的:÷==倍,故③错误;
乙的平均速度是甲的==倍,故④正确;
故选:C.
二.填空题
11.如果y=++2,那么xy的值是 25 .
【分析】根据二次根式有意义的条件列不等式组求解确定x和y的值,从而代入求值.
解:由题意可得,
解得:x=5,
∴y==2,
∴原式=52=25,
故答案为:25.
12.命题“等腰三角形的两个底角相等”的逆命题是 两个角相等三角形是等腰三角形 .
【分析】先找到原命题的题设和结论,再将题设和结论互换,即可而得到原命题的逆命题.
解:因为原命题的题设是:“一个三角形是等腰三角形”,结论是“这个三角形两底角相等”,
所以命题“等腰三角形的两个底角相等”的逆命题是“两个角相等三角形是等腰三角形”.
13.若不等式组的解集为x≤﹣m,则m ≥ n.
【分析】根据口诀:同小取小可得﹣m≤﹣n,再由不等式的基本性质即可得出答案.
解:∵不等式组的解集为x≤﹣m,
∴﹣m≤﹣n,
则m≥n,
故答案为:≥.
14.在Rt△ABC中,∠A=90°,BC=10,AB=6,点P在AB上且P到另两边的距离相等,则AP的长为 .
【分析】根据勾股定理求出AC的值,过点P作PD⊥BC于D,进而利用勾股定理解答即可.
解:如图所示:过点P作PD⊥BC于D,连接PC,
∵∠A=90°,BC=10,AB=6,
∴AC=,
∵点P在AB上且P到另两边的距离相等,
∴PA=PD,
设AP=x,BP=6﹣x,
在Rt△APC与Rt△DPC中,
,
∴Rt△APC≌Rt△DPC(HL),
∴CD=AC=8,
∴BD=BC﹣CD=10﹣8=2,
在Rt△BPD中,BP2=PD2+BD2,
即(6﹣x)2=x2+22,
解得:x=,
∴AP=.
故答案为:.
15.如图,直线l1:y=kx+5与直线l2:y=﹣x+n交于点P(﹣1,3),则不等式kx+5>﹣x+n
的解集为 x>﹣1 .
【分析】写出直线y=kx+5在直线y=﹣x+n上方部分的x的取值范围即可.
解:由图可知,当x>﹣1时,直线y=kx+5在直线y=﹣x+n上方,
所以不等式kx+5>﹣x+n的解集为x>﹣1;
故答案为:x>﹣1.
16.如图,在△ABC中,AB=AC,D为BC上的一点,∠BAD=28°,在AD的右侧作△ACE,使得AE=AD,∠DAE=∠BAC,连接CE,DE,DE交AC于点O,若CE∥AB,则∠DOC的度数为 92° .
【分析】根据已知条件证明△DAB≌△EAC,可得∠B=∠ACE,再根据CE∥AB,可得∠B+∠ACB+∠ACE=180°,然后证明△ABC是等边三角形,△ADE是等边三角形,进而根据三角形内角和定理即可解决问题.
解:∵∠DAE=∠BAC,
∴∠DAE﹣∠DAC=∠BAC﹣∠DAC,
∴∠DAB=∠EAC,
在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴∠B=∠ACE,
∵CE∥AB,
∴∠B+∠BCE=180°,
∴∠B+∠ACB+∠ACE=180°,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠ACB=∠ACE=60°,
∴△ABC是等边三角形,
∴∠DAE=∠BAC=60°,
∴△ADE是等边三角形,
∴∠ADE=60°,
∵∠BAD=28°,
∴∠OAD=60°﹣28°=32°,
∴∠DOC=∠OAD+∠ADE=32°+60°=92°.
故答案为:92°.
三.解答题
17.计算:
(1);
(2).
【分析】(1)利用二次根式的乘法与除法法则运算;
(2)先把各二次根式化为最简二次根式,然后合并即可.
解:(1)原式=
=
=;
(2)原式=3+﹣2+
=+2.
18.(1);
(2)+2=.
【分析】(1)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:(1),
由①得:x≤,
由②得:x>﹣2,
∴不等式组的解集为﹣2<x≤;
(2)去分母得:1+2(x﹣2)=x﹣1,
解得:x=2,
检验:把x=2代入得:x﹣2=0,
∴x=2是增根,分式方程无解.
19.小聪去购买笔记本和钢笔共30件,每本笔记本2元,每支钢笔5元,若购买的钢笔数量不少于笔记本的数量.
(1)小聪至多能买几本笔记本?
(2)若小聪只带了130元钱,此时他至少要买几本笔记本?
【分析】(1)设小聪买x本笔记本,则买(30﹣x)支钢笔,由题意:购买的钢笔数量不少于笔记本的数量.列出一元一次不等式,解不等式即可;
(2)设小聪买y本笔记本,则买(30﹣y)支钢笔,由题意:每本笔记本2元,每支钢笔5元,小聪只带了130元钱,列出一元一次不等式,解不等式即可.
解:(1)设小聪买x本笔记本,则买(30﹣x)支钢笔,
由题意得:30﹣x≥x,
解得:x≤15,
答:小聪至多能买15本笔记本;
(2)设小聪买y本笔记本,则买(30﹣y)支钢笔,
由题意得:2y+5(30﹣y)≤130,
解得:y≥6,
答:若小聪只带了130元钱,此时他至少要买7本笔记本.
20.已知一次函数y=kx+b的图象过(1,6)和(﹣1,2).
(1)求一次函数y=kx+b的关系式;
(2)求一次函数y=kx+b的图象与坐标轴围成的三角形的面积.
【分析】(1)把已知点的坐标代入y=kx+b得到k、b的方程组,然后解方程组即可;
(2)利用坐标轴点的坐标特征求出一次函数与x轴和y轴的交点坐标,然后利用三角形面积公式求解.
解:(1)根据题意得,
解得,
所以一次函数解析式为y=2x+4;
(2)当x=0时,y=2x+4=4,则一次函数图象与y轴的交点坐标为(0,4),
当y=0时,2x+4=0,解得x=﹣2,则一次函数图象与x轴的交点坐标为(﹣2,0),
所以一次函数y=kx+b的图象与坐标轴围成的三角形的面积=×2×4=4.
21.如图,在△ABC中,AB=AC,D为CA延长线上一点,且DE⊥BC交AB于点F.
(1)求证:△ADF是等腰三角形;
(2)若AC=10,BE=3,F为AB中点,求DF的长.
【分析】(1)利用等腰三角形的性质可得∠B=∠C,再利用等角的余角相等证明∠D=∠AFD即可解答;
(2)由(1)得△ADF是等腰三角形,想到等腰三角形的三线合一性质,所以过点A作AG⊥DE,垂足为G,先在Rt△BEF中,利用勾股定理求出EF的长,然后证明△AGF≌△BEF即可解答.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠DEC=∠DEB=90°,
∴∠B+∠BFE=90°,∠C+∠D=90°,
∴∠D=∠BFE,
∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴AD=AF,
∴△ADF是等腰三角形;
(2)过点A作AG⊥DE,垂足为G,
∵AB=AC,AC=10,
∴AB=10,
∵F为AB中点,
∴AF=BF=AB=5,
在Rt△BFE中,BE=3,
∴EF===4,
∵∠AGF=∠BEF=90°,∠AFG=∠BFE,
∴△AFG≌△BFE(AAS),
∴GF=EF=4,
∵AD=AF,AG⊥DF,
∴DF=2GF=8.
22.如图,在△ABC中,AB=AC,点D在AC边上(不与点A,点C重合),连接BD,BD=AB.
(1)设∠C=α,∠ABD=β.
①当α=50°时,求β.
②直接写出β与α之间的等量关系及α的取值范围.
(2)若AB=5,BC=6,求AD的长.
【分析】(1)①由等腰三角形的性质得出∠ABC=∠C=50°,则可求出答案;
②由等腰三角形的性质得出∠A=∠ADB,∠ABC=∠C=α,则可求出β,由三角形外角的性质可得出答案;
(2)过点B作BM⊥BC于点M,BN⊥AC于点N,由勾股定理可得出AM=4,由勾股定理得出25﹣x2=36﹣(5﹣x)2,则可得出答案.
解:(1)①∵AB=AC,
∴∠ABC=∠C=50°,
∴∠A=180°﹣∠ABC﹣∠C=80°,
∵BD=AB,
∴∠BDA=∠A=80°,
∴β=180°﹣∠A﹣∠BDA=20°;
②∵AB=BD,
∴∠A=∠ADB,
∴β=180°﹣2∠A,
又∵AB=AC,
∴∠ABC=∠C=α,
∴∠A=180°﹣2∠C=180°﹣2α,
∴β=180°﹣2(180°﹣2α)
=4α﹣180°;
∵∠A=∠ADB,∠ADB>∠C,
∴180°﹣2α>α,
∴α<60°,
又∵4α﹣180°>0,
∴α>45°,
∴α的取值范围是45°<α<60°;
(2)过点B作BM⊥BC于点M,BN⊥AC于点N,
设AN=x,则CN=5﹣x,
∵AB=5,BC=6,
∴AM===4,
∵BN2=AB2﹣AN2=BC2﹣CN2,
∴25﹣x2=36﹣(5﹣x)2,
∴x=,
∴AD=2AN=.
23.设函数y1=ax+b,y2=bx+a(a,b为常数,ab≠0且a≠b),函数y和y的图象的交点为点P.
(1)求证:点P在y轴的右侧.
(2)已知点P在第一象限,函数y的值随x的增大而增大.
①当x=2时,y1﹣y2=2,求a的取值范围.
②若点P的坐标是(1,1),且a>b,求证:当x=2时,y1﹣y2<﹣.
【分析】(1)由ax+b=bx+a,解得x=1,即知点P在y轴的右侧.
(2)①由函数y2的值随x的增大而增大,得b>0,点P在第一象限,可得a+b>0,当x=2时,y2﹣y1=2,可得b=a﹣2,即可得a>2;
②根据点P的坐标是(1,1),知b=1﹣a,由a>b,b>0,可得<a<1,而当x=2时,y2﹣y1=2a﹣1,﹣=,即可证明y1﹣y2<﹣.
【解答】(1)证明:令ax+b=bx+a,解得x=1,
∴函数y1和y2的图象的交点P的横坐标为1,
∴点P在y轴的右侧.
(2)解:①∵函数y2的值随x的增大而增大,
∴b>0,
由(1)知P(1,a+b),
∵点P在第一象限,
∴a+b>0,
当x=2时,y1=2a+b,y2=2b+a,
∵y2﹣y1=2,
∴(2a+b)﹣(2b+a)=2,
∴a﹣b=2,即b=a﹣2,
∵b>0,
∴a﹣2>0,
∴a>2;
此时满足a+b>0,
∴a的取值范围是a>2;
②证明:∵点P的坐标是(1,1),
∴a+b=1,
∴b=1﹣a,
∵a>b,b>0,
∴a>1﹣a且1﹣a>0,
∴<a<1,
当x=2时,y1﹣y2=(2a+b)﹣(2b+a)=a﹣b=a﹣(1﹣a)=2a﹣1,
﹣=﹣==,
∵<a<1,
∴0<a(1﹣a)<1,2a﹣1>0,
∴>1,
∴>2a﹣1,
∴y1﹣y2<﹣.
一、选择题
1.下列冬奥会会徽中,属于轴对称图形的是( )
A. B.
C. D.
2.有下列长度的三条线段,其中能组成三角形的是( )
A.4,5,9 B.2.5,6.5,10 C.3,4,5 D.5,12,17
3.点P(a,1)在第一象限,则a的取值范围是( )
A.a>0 B.a≥0 C.a<0 D.a≤0
4.下列各式中,是二次根式有( )
①;②;③;④;⑤;⑥.
A.2个 B.3个 C.4个 D.5个
5.若x>y,则下列式子中错误的是( )
A.x﹣2>y﹣2 B.x+2>y+2 C.﹣2x>﹣2y D.>
6.一次函数y=kx﹣2k的大致图象是( )
A. B.
C. D.
7.在一幅长60cm,宽40cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是2816cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.(60+x)(40+2x)=2816 B.(60+x)(40+x)=2816
C.(60+2x)(40+x)=2816 D.(60+2x)(40+2x)=2816
8.已知点A的坐标为(a+1,3﹣a),点A关于x轴的对称点A'落在一次函数y=2x+1的图象上,则a的值可以是( )
A.﹣4 B.﹣5 C.﹣6 D.﹣7
9.如图,在△ABC中,点P在边BC上(不与点B,点C重合),( )
A.若∠BAC=90°,∠BAP=∠B,则AC=PC
B.若∠BAC=90°,∠BAP=∠C,则AP⊥BC
C.若AP⊥BC,PB=PC,则∠BAC=90°
D.若PB=PC,∠BAP=∠CAP,则∠BAC=90°
10.如图为甲、乙两人训练跑步中路程s关于时间t的函数图象,下列信息:①甲跑800m用了150s;②乙跑400m用了90s;③甲的平均速度是乙的倍;④乙的平均速度是甲的倍,其中正确的是( )
A.①③ B.②③ C.①④ D.②④
二.填空题
11.如果y=++2,那么xy的值是 .
12.命题“等腰三角形的两个底角相等”的逆命题是 .
13.若不等式组的解集为x≤﹣m,则m n.
14.在Rt△ABC中,∠A=90°,BC=10,AB=6,点P在AB上且P到另两边的距离相等,则AP的长为 .
15.如图,直线l1:y=kx+5与直线l2:y=﹣x+n交于点P(﹣1,3),则不等式kx+5>﹣x+n
的解集为 .
16.如图,在△ABC中,AB=AC,D为BC上的一点,∠BAD=28°,在AD的右侧作△ACE,使得AE=AD,∠DAE=∠BAC,连接CE,DE,DE交AC于点O,若CE∥AB,则∠DOC的度数为 .
三.解答题
17.计算:
(1);
(2).
18.(1);
(2)+2=.
19.小聪去购买笔记本和钢笔共30件,每本笔记本2元,每支钢笔5元,若购买的钢笔数量不少于笔记本的数量.
(1)小聪至多能买几本笔记本?
(2)若小聪只带了130元钱,此时他至少要买几本笔记本?
20.已知一次函数y=kx+b的图象过(1,6)和(﹣1,2).
(1)求一次函数y=kx+b的关系式;
(2)求一次函数y=kx+b的图象与坐标轴围成的三角形的面积.
21.如图,在△ABC中,AB=AC,D为CA延长线上一点,且DE⊥BC交AB于点F.
(1)求证:△ADF是等腰三角形;
(2)若AC=10,BE=3,F为AB中点,求DF的长.
22.如图,在△ABC中,AB=AC,点D在AC边上(不与点A,点C重合),连接BD,BD=AB.
(1)设∠C=α,∠ABD=β.
①当α=50°时,求β.
②直接写出β与α之间的等量关系及α的取值范围.
(2)若AB=5,BC=6,求AD的长.
23.设函数y1=ax+b,y2=bx+a(a,b为常数,ab≠0且a≠b),函数y和y的图象的交点为点P.
(1)求证:点P在y轴的右侧.
(2)已知点P在第一象限,函数y的值随x的增大而增大.
①当x=2时,y1﹣y2=2,求a的取值范围.
②若点P的坐标是(1,1),且a>b,求证:当x=2时,y1﹣y2<﹣.
参考答案
一、选择题
1.下列冬奥会会徽中,属于轴对称图形的是( )
A. B.
C. D.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
解:选项A、B、C不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:D.
2.有下列长度的三条线段,其中能组成三角形的是( )
A.4,5,9 B.2.5,6.5,10 C.3,4,5 D.5,12,17
【分析】三角形的三条边必须满足:任意两边之和>第三边,任意两边之差<第三边.
解:A、4+5=9,故不能组成三角形,不符合题意;
B、2.5+6.5<10,不能组成三角形,不符合题意;
C、4+3>5,能组成三角形,符合题意;
D、5+12=17,不能组成三角形,不符合题意;
故选:C.
3.点P(a,1)在第一象限,则a的取值范围是( )
A.a>0 B.a≥0 C.a<0 D.a≤0
【分析】由第一象限内点的坐标符号特点求解即可.
解:∵点P(a,1)在第一象限,
∴a>0,
故选:A.
4.下列各式中,是二次根式有( )
①;②;③;④;⑤;⑥.
A.2个 B.3个 C.4个 D.5个
【分析】根据二次根式的概念进行分析判断.
解:①是二次根式,
②没有意义,不是二次根式,
③是三次根式,不是二次根式,
④没有意义,不是二次根式,
⑤是二次根式,
⑥是二次根式,
∴①⑤⑥是二次根式,共3个,
故选:B.
5.若x>y,则下列式子中错误的是( )
A.x﹣2>y﹣2 B.x+2>y+2 C.﹣2x>﹣2y D.>
【分析】A:不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变,据此判断即可.
B:不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变,据此判断即可.
C:不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变,据此判断即可.
D:不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变,据此判断即可.
解:∵x>y,
∴x﹣2>y﹣2,
∴选项A正确;
∵x>y,
∴x+2>y+2,
∴选项B正确;
∵x>y,
∴﹣2x<﹣2y,
∴选项C不正确;
∵x>y,
∴,
∴选项D正确.
故选:C.
6.一次函数y=kx﹣2k的大致图象是( )
A. B.
C. D.
【分析】一次函数解析式为y=kx﹣2k,易得其图象与x轴的交点为(2,0),分析选项可得答案.
解:函数的解析式为y=kx﹣2k
即函数图象与x轴的交点为(2,0),
分析可得,B选项符合题意.
故选:B.
7.在一幅长60cm,宽40cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是2816cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.(60+x)(40+2x)=2816 B.(60+x)(40+x)=2816
C.(60+2x)(40+x)=2816 D.(60+2x)(40+2x)=2816
【分析】根据题意可知:矩形挂图的长为(60+2x)cm,宽为(40+2x)cm;则运用面积公式列方程即可.
解:挂图长为(60+2x)cm,宽为(40+2x)cm,
所以根据矩形的面积公式可得:(60+2x)(40+2x)=2816.
故选:D.
8.已知点A的坐标为(a+1,3﹣a),点A关于x轴的对称点A'落在一次函数y=2x+1的图象上,则a的值可以是( )
A.﹣4 B.﹣5 C.﹣6 D.﹣7
【分析】根据对称的性质求出点A′的坐标,再把点A′的坐标代入y=2x+1,即可求出a.
解:∵点A的坐标为(a+1,3﹣a),
∴点A关于x轴的对称点A'的坐标是(a+1,﹣3+a),
∵点A′在一次函数y=2x+1的图象上,
∴﹣3+a=2(a+1)+1,
解得:a=﹣6,
故选:C.
9.如图,在△ABC中,点P在边BC上(不与点B,点C重合),( )
A.若∠BAC=90°,∠BAP=∠B,则AC=PC
B.若∠BAC=90°,∠BAP=∠C,则AP⊥BC
C.若AP⊥BC,PB=PC,则∠BAC=90°
D.若PB=PC,∠BAP=∠CAP,则∠BAC=90°
【分析】根据直角三角形的性质逐项判定可求解.
解:A.∵∠BAC=90°,
∴∠BAP+∠CAP=∠B+∠C=90°,
∵∠BAP=∠B,
∴∠CAP=∠C,
∴AP=PC,
只有当∠B=30°时,AC=PC,故错误;
B.∵∠BAC=90°,
∴∠BAP+∠CAP=90°,
∵∠BAP=∠C,
∴∠C+∠CAP=90°,
∴∠APC=180°﹣(∠C+∠CAP)=90°,
即AP⊥BC,故正确;
C.∵AP⊥BC,PB=PC,
∴AP垂直平分BC,
而∠BAC不一定等于90°,故错误;
D.根据PB=PC,∠BAP=∠CAP,无法证明∠BAC=90°,故错误,
故选:B.
10.如图为甲、乙两人训练跑步中路程s关于时间t的函数图象,下列信息:①甲跑800m用了150s;②乙跑400m用了90s;③甲的平均速度是乙的倍;④乙的平均速度是甲的倍,其中正确的是( )
A.①③ B.②③ C.①④ D.②④
【分析】根据函数图象中的数据,可以直接判断①、②,再根据图象中的数据,计算出甲、乙的速度,然后即可判断③、④.
解:由图象可得,
甲跑800m用了150s,故①正确;
乙跑400m用了150﹣90=60(s),故②错误;
甲的平均速度是800÷150=(m/s),乙的平均速度是400÷60=(m/s),
则甲的平均速度是乙的:÷==倍,故③错误;
乙的平均速度是甲的==倍,故④正确;
故选:C.
二.填空题
11.如果y=++2,那么xy的值是 25 .
【分析】根据二次根式有意义的条件列不等式组求解确定x和y的值,从而代入求值.
解:由题意可得,
解得:x=5,
∴y==2,
∴原式=52=25,
故答案为:25.
12.命题“等腰三角形的两个底角相等”的逆命题是 两个角相等三角形是等腰三角形 .
【分析】先找到原命题的题设和结论,再将题设和结论互换,即可而得到原命题的逆命题.
解:因为原命题的题设是:“一个三角形是等腰三角形”,结论是“这个三角形两底角相等”,
所以命题“等腰三角形的两个底角相等”的逆命题是“两个角相等三角形是等腰三角形”.
13.若不等式组的解集为x≤﹣m,则m ≥ n.
【分析】根据口诀:同小取小可得﹣m≤﹣n,再由不等式的基本性质即可得出答案.
解:∵不等式组的解集为x≤﹣m,
∴﹣m≤﹣n,
则m≥n,
故答案为:≥.
14.在Rt△ABC中,∠A=90°,BC=10,AB=6,点P在AB上且P到另两边的距离相等,则AP的长为 .
【分析】根据勾股定理求出AC的值,过点P作PD⊥BC于D,进而利用勾股定理解答即可.
解:如图所示:过点P作PD⊥BC于D,连接PC,
∵∠A=90°,BC=10,AB=6,
∴AC=,
∵点P在AB上且P到另两边的距离相等,
∴PA=PD,
设AP=x,BP=6﹣x,
在Rt△APC与Rt△DPC中,
,
∴Rt△APC≌Rt△DPC(HL),
∴CD=AC=8,
∴BD=BC﹣CD=10﹣8=2,
在Rt△BPD中,BP2=PD2+BD2,
即(6﹣x)2=x2+22,
解得:x=,
∴AP=.
故答案为:.
15.如图,直线l1:y=kx+5与直线l2:y=﹣x+n交于点P(﹣1,3),则不等式kx+5>﹣x+n
的解集为 x>﹣1 .
【分析】写出直线y=kx+5在直线y=﹣x+n上方部分的x的取值范围即可.
解:由图可知,当x>﹣1时,直线y=kx+5在直线y=﹣x+n上方,
所以不等式kx+5>﹣x+n的解集为x>﹣1;
故答案为:x>﹣1.
16.如图,在△ABC中,AB=AC,D为BC上的一点,∠BAD=28°,在AD的右侧作△ACE,使得AE=AD,∠DAE=∠BAC,连接CE,DE,DE交AC于点O,若CE∥AB,则∠DOC的度数为 92° .
【分析】根据已知条件证明△DAB≌△EAC,可得∠B=∠ACE,再根据CE∥AB,可得∠B+∠ACB+∠ACE=180°,然后证明△ABC是等边三角形,△ADE是等边三角形,进而根据三角形内角和定理即可解决问题.
解:∵∠DAE=∠BAC,
∴∠DAE﹣∠DAC=∠BAC﹣∠DAC,
∴∠DAB=∠EAC,
在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴∠B=∠ACE,
∵CE∥AB,
∴∠B+∠BCE=180°,
∴∠B+∠ACB+∠ACE=180°,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠ACB=∠ACE=60°,
∴△ABC是等边三角形,
∴∠DAE=∠BAC=60°,
∴△ADE是等边三角形,
∴∠ADE=60°,
∵∠BAD=28°,
∴∠OAD=60°﹣28°=32°,
∴∠DOC=∠OAD+∠ADE=32°+60°=92°.
故答案为:92°.
三.解答题
17.计算:
(1);
(2).
【分析】(1)利用二次根式的乘法与除法法则运算;
(2)先把各二次根式化为最简二次根式,然后合并即可.
解:(1)原式=
=
=;
(2)原式=3+﹣2+
=+2.
18.(1);
(2)+2=.
【分析】(1)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:(1),
由①得:x≤,
由②得:x>﹣2,
∴不等式组的解集为﹣2<x≤;
(2)去分母得:1+2(x﹣2)=x﹣1,
解得:x=2,
检验:把x=2代入得:x﹣2=0,
∴x=2是增根,分式方程无解.
19.小聪去购买笔记本和钢笔共30件,每本笔记本2元,每支钢笔5元,若购买的钢笔数量不少于笔记本的数量.
(1)小聪至多能买几本笔记本?
(2)若小聪只带了130元钱,此时他至少要买几本笔记本?
【分析】(1)设小聪买x本笔记本,则买(30﹣x)支钢笔,由题意:购买的钢笔数量不少于笔记本的数量.列出一元一次不等式,解不等式即可;
(2)设小聪买y本笔记本,则买(30﹣y)支钢笔,由题意:每本笔记本2元,每支钢笔5元,小聪只带了130元钱,列出一元一次不等式,解不等式即可.
解:(1)设小聪买x本笔记本,则买(30﹣x)支钢笔,
由题意得:30﹣x≥x,
解得:x≤15,
答:小聪至多能买15本笔记本;
(2)设小聪买y本笔记本,则买(30﹣y)支钢笔,
由题意得:2y+5(30﹣y)≤130,
解得:y≥6,
答:若小聪只带了130元钱,此时他至少要买7本笔记本.
20.已知一次函数y=kx+b的图象过(1,6)和(﹣1,2).
(1)求一次函数y=kx+b的关系式;
(2)求一次函数y=kx+b的图象与坐标轴围成的三角形的面积.
【分析】(1)把已知点的坐标代入y=kx+b得到k、b的方程组,然后解方程组即可;
(2)利用坐标轴点的坐标特征求出一次函数与x轴和y轴的交点坐标,然后利用三角形面积公式求解.
解:(1)根据题意得,
解得,
所以一次函数解析式为y=2x+4;
(2)当x=0时,y=2x+4=4,则一次函数图象与y轴的交点坐标为(0,4),
当y=0时,2x+4=0,解得x=﹣2,则一次函数图象与x轴的交点坐标为(﹣2,0),
所以一次函数y=kx+b的图象与坐标轴围成的三角形的面积=×2×4=4.
21.如图,在△ABC中,AB=AC,D为CA延长线上一点,且DE⊥BC交AB于点F.
(1)求证:△ADF是等腰三角形;
(2)若AC=10,BE=3,F为AB中点,求DF的长.
【分析】(1)利用等腰三角形的性质可得∠B=∠C,再利用等角的余角相等证明∠D=∠AFD即可解答;
(2)由(1)得△ADF是等腰三角形,想到等腰三角形的三线合一性质,所以过点A作AG⊥DE,垂足为G,先在Rt△BEF中,利用勾股定理求出EF的长,然后证明△AGF≌△BEF即可解答.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠DEC=∠DEB=90°,
∴∠B+∠BFE=90°,∠C+∠D=90°,
∴∠D=∠BFE,
∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴AD=AF,
∴△ADF是等腰三角形;
(2)过点A作AG⊥DE,垂足为G,
∵AB=AC,AC=10,
∴AB=10,
∵F为AB中点,
∴AF=BF=AB=5,
在Rt△BFE中,BE=3,
∴EF===4,
∵∠AGF=∠BEF=90°,∠AFG=∠BFE,
∴△AFG≌△BFE(AAS),
∴GF=EF=4,
∵AD=AF,AG⊥DF,
∴DF=2GF=8.
22.如图,在△ABC中,AB=AC,点D在AC边上(不与点A,点C重合),连接BD,BD=AB.
(1)设∠C=α,∠ABD=β.
①当α=50°时,求β.
②直接写出β与α之间的等量关系及α的取值范围.
(2)若AB=5,BC=6,求AD的长.
【分析】(1)①由等腰三角形的性质得出∠ABC=∠C=50°,则可求出答案;
②由等腰三角形的性质得出∠A=∠ADB,∠ABC=∠C=α,则可求出β,由三角形外角的性质可得出答案;
(2)过点B作BM⊥BC于点M,BN⊥AC于点N,由勾股定理可得出AM=4,由勾股定理得出25﹣x2=36﹣(5﹣x)2,则可得出答案.
解:(1)①∵AB=AC,
∴∠ABC=∠C=50°,
∴∠A=180°﹣∠ABC﹣∠C=80°,
∵BD=AB,
∴∠BDA=∠A=80°,
∴β=180°﹣∠A﹣∠BDA=20°;
②∵AB=BD,
∴∠A=∠ADB,
∴β=180°﹣2∠A,
又∵AB=AC,
∴∠ABC=∠C=α,
∴∠A=180°﹣2∠C=180°﹣2α,
∴β=180°﹣2(180°﹣2α)
=4α﹣180°;
∵∠A=∠ADB,∠ADB>∠C,
∴180°﹣2α>α,
∴α<60°,
又∵4α﹣180°>0,
∴α>45°,
∴α的取值范围是45°<α<60°;
(2)过点B作BM⊥BC于点M,BN⊥AC于点N,
设AN=x,则CN=5﹣x,
∵AB=5,BC=6,
∴AM===4,
∵BN2=AB2﹣AN2=BC2﹣CN2,
∴25﹣x2=36﹣(5﹣x)2,
∴x=,
∴AD=2AN=.
23.设函数y1=ax+b,y2=bx+a(a,b为常数,ab≠0且a≠b),函数y和y的图象的交点为点P.
(1)求证:点P在y轴的右侧.
(2)已知点P在第一象限,函数y的值随x的增大而增大.
①当x=2时,y1﹣y2=2,求a的取值范围.
②若点P的坐标是(1,1),且a>b,求证:当x=2时,y1﹣y2<﹣.
【分析】(1)由ax+b=bx+a,解得x=1,即知点P在y轴的右侧.
(2)①由函数y2的值随x的增大而增大,得b>0,点P在第一象限,可得a+b>0,当x=2时,y2﹣y1=2,可得b=a﹣2,即可得a>2;
②根据点P的坐标是(1,1),知b=1﹣a,由a>b,b>0,可得<a<1,而当x=2时,y2﹣y1=2a﹣1,﹣=,即可证明y1﹣y2<﹣.
【解答】(1)证明:令ax+b=bx+a,解得x=1,
∴函数y1和y2的图象的交点P的横坐标为1,
∴点P在y轴的右侧.
(2)解:①∵函数y2的值随x的增大而增大,
∴b>0,
由(1)知P(1,a+b),
∵点P在第一象限,
∴a+b>0,
当x=2时,y1=2a+b,y2=2b+a,
∵y2﹣y1=2,
∴(2a+b)﹣(2b+a)=2,
∴a﹣b=2,即b=a﹣2,
∵b>0,
∴a﹣2>0,
∴a>2;
此时满足a+b>0,
∴a的取值范围是a>2;
②证明:∵点P的坐标是(1,1),
∴a+b=1,
∴b=1﹣a,
∵a>b,b>0,
∴a>1﹣a且1﹣a>0,
∴<a<1,
当x=2时,y1﹣y2=(2a+b)﹣(2b+a)=a﹣b=a﹣(1﹣a)=2a﹣1,
﹣=﹣==,
∵<a<1,
∴0<a(1﹣a)<1,2a﹣1>0,
∴>1,
∴>2a﹣1,
∴y1﹣y2<﹣.
同课章节目录
