2021-2022学年四川省内江市东兴区六中八年级(下)入学数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年四川省内江市东兴区六中八年级(下)入学数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 15:20:01 | ||
图片预览


文档简介
2021-2022学年四川省内江市东兴区六中八年级(下)入学数学试卷
一、选择题
1.下列运算正确的是( )
A.x x2=x2 B.(xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
2.实数a在数轴上的对应点位置如图所示,若实数b满足:|b|<a,则b的值可以是( )
A.﹣3 B.﹣2 C.3 D.4
3.在一个样本中,50个数据分别落在5个小组内,第1、2、3、5小组数据的个数分别是2、8、15、5,则第4小组的频率是( )
A.0.6 B.20 C.0.4 D.30
4.已知y=++9,则y+x的平方根是( )
A.3 B.±3 C.4 D.±4
5.若分式有意义,则x的取值范围是( )
A.x≠2 B.x≠﹣2 C.x≠4 D.x≠﹣4
6.如果把分式中的x,y同时变为原来的4倍,那么该分式的值( )
A.不变 B.变为原来的4倍
C.变为原来的 D.变为原来的
7.如图,在△ABC中,∠C=90°,AC=16,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,则△ABC的面积为( )
A.16 B.32 C.48 D.64
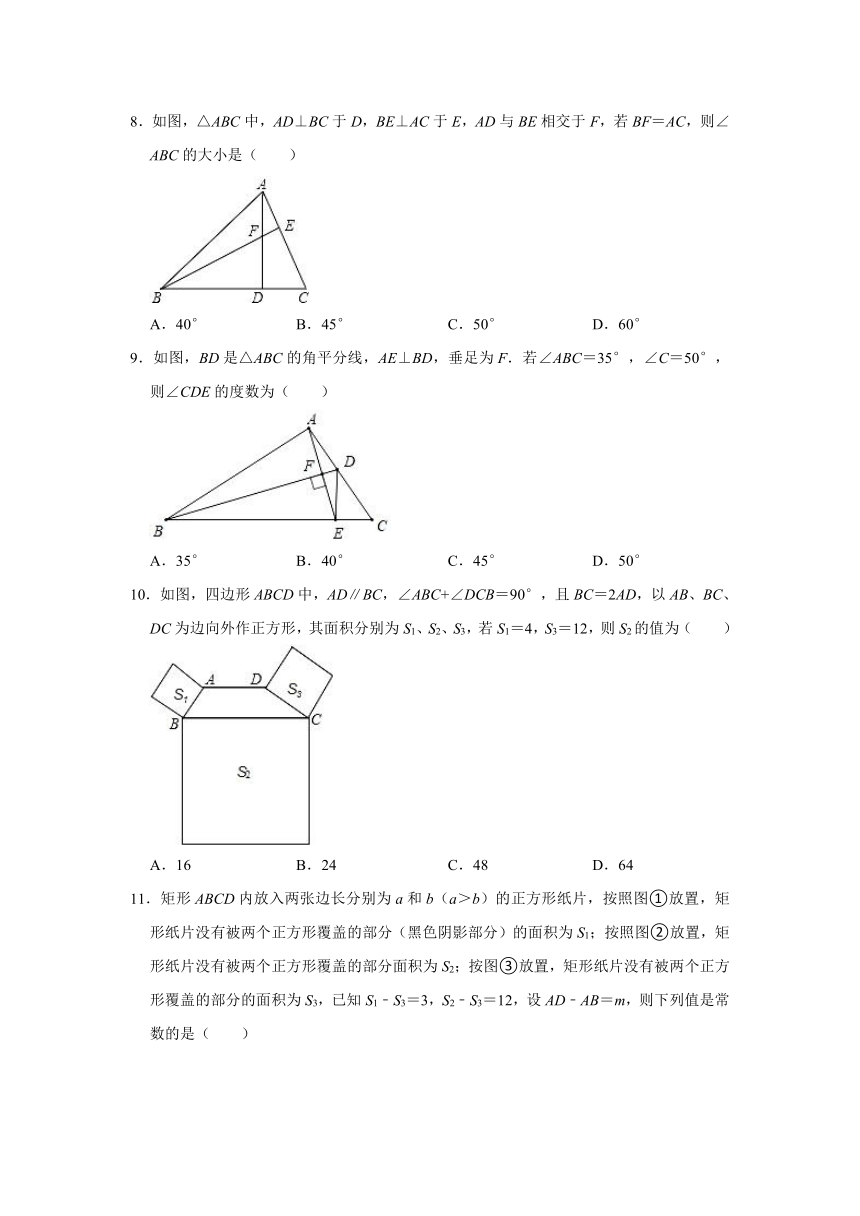
8.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是( )
A.40° B.45° C.50° D.60°
9.如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
10.如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=4,S3=12,则S2的值为( )
A.16 B.24 C.48 D.64
11.矩形ABCD内放入两张边长分别为a和b(a>b)的正方形纸片,按照图①放置,矩形纸片没有被两个正方形覆盖的部分(黑色阴影部分)的面积为S1;按照图②放置,矩形纸片没有被两个正方形覆盖的部分面积为S2;按图③放置,矩形纸片没有被两个正方形覆盖的部分的面积为S3,已知S1﹣S3=3,S2﹣S3=12,设AD﹣AB=m,则下列值是常数的是( )
A.ma B.mb C.m D.a+b
12.如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①DC′平分∠BDE;②BC长为2a+b;③△BDC′是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( )
A.①②④ B.②③④ C.②③ D.②④
二、填空题(共5小题,满分15分)
13.因式分解:xy2+2xy+x= .
14.若2m+2m+2m+2m=8,则m= .
15.在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为 cm2.
16.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.E为线段BD上一点,连结CE,将边BC沿CE折叠,使点B的对称点B'落在CD的延长线上.若AB=10,BC=8,则△ACE的面积为 .
17.如图,已知在△ABC中,AB=AC,∠BAC=90,直角∠EPF顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下4个结论:①AE=CF,②△EPF是等腰Rt△,③S四边形AEPF=S△ABC,④EF=AP.当∠EPF在△ABC内部绕顶点P旋转时(点E不与AB重合),上述结论始终成立的是 .
三、解答题(共6小题,满分31分)
18.计算:﹣12018+()﹣2++(π﹣2019)0﹣|﹣2|.
19.已知(x+y)2=1,(x﹣y)2=49,求x2+y2与xy的值.
20.已知a=,b=,求代数式[(ab+1)(ab﹣2)﹣2a2b2+2]÷(﹣ab)的值.
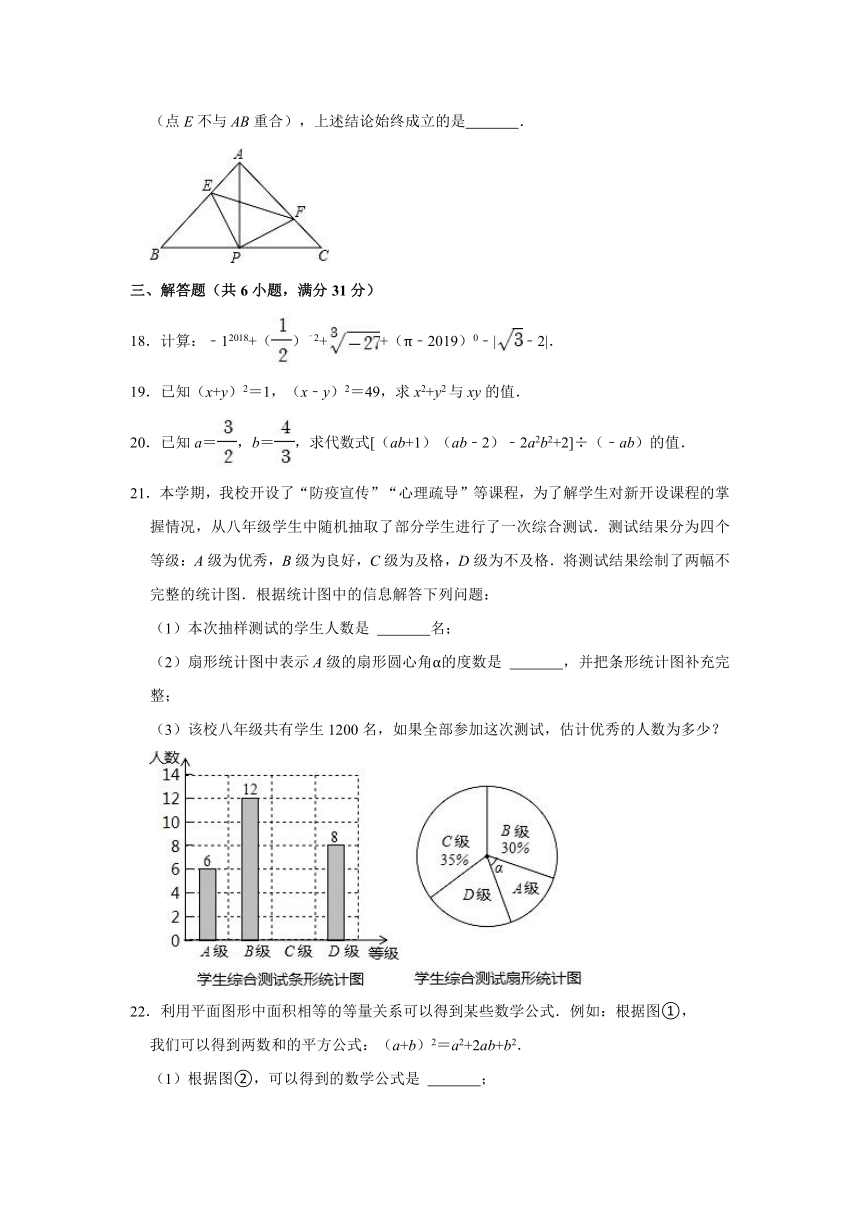
21.本学期,我校开设了“防疫宣传”“心理疏导”等课程,为了解学生对新开设课程的掌握情况,从八年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了两幅不完整的统计图.根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 名;
(2)扇形统计图中表示A级的扇形圆心角α的度数是 ,并把条形统计图补充完整;
(3)该校八年级共有学生1200名,如果全部参加这次测试,估计优秀的人数为多少?
22.利用平面图形中面积相等的等量关系可以得到某些数学公式.例如:根据图①,
我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.
(1)根据图②,可以得到的数学公式是 ;
(2)根据图③,请写出(a+b)、(a﹣b)、ab的等量关系是 .
(3)根据图④,请写出一个等式: ;
(4)小明同学使用图⑤中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片,恰好拼成一个面积为(3a+b)(a+3b)的长方形,则可得x+y+z的值为 ;
(5)类似地,利用立体图形体积的等量关系也可以得到某些数学公式.现请你根据图⑥,写出一个等式: .
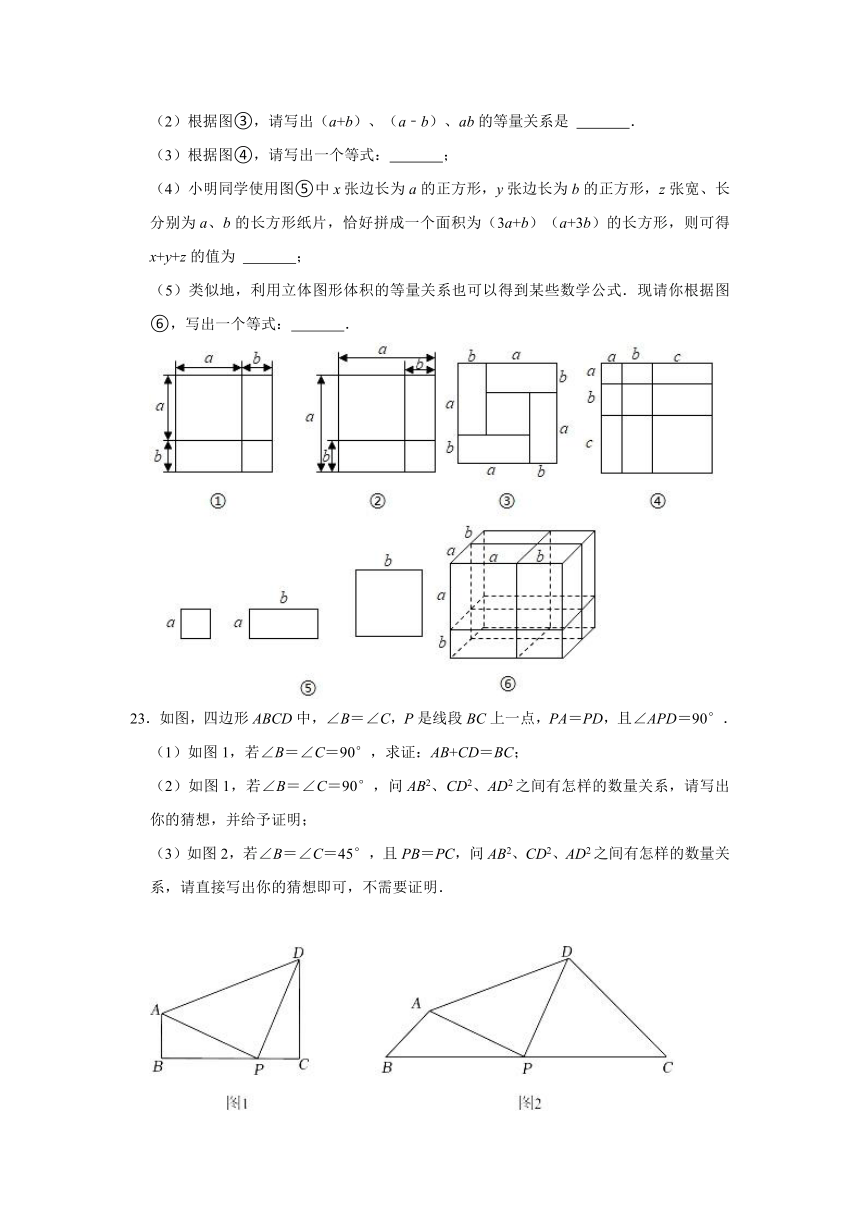
23.如图,四边形ABCD中,∠B=∠C,P是线段BC上一点,PA=PD,且∠APD=90°.
(1)如图1,若∠B=∠C=90°,求证:AB+CD=BC;
(2)如图1,若∠B=∠C=90°,问AB2、CD2、AD2之间有怎样的数量关系,请写出你的猜想,并给予证明;
(3)如图2,若∠B=∠C=45°,且PB=PC,问AB2、CD2、AD2之间有怎样的数量关系,请直接写出你的猜想即可,不需要证明.
参考答案
一、选择
1.下列运算正确的是( )
A.x x2=x2 B.(xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
【分析】根据同底数幂的除法,底数不变指数相减,合并同类项,系数相加字母和字母的指数不变,同底数幂的乘法,底数不变指数相加,幂的乘方,底数不变指数相乘,对各选项计算后利用排除法求解.
解:A、x x2=x3同底数幂的乘法,底数不变指数相加,故本选项错误;
B、(xy)2=x2y2,幂的乘方,底数不变指数相乘,故本选项错误;
C、(x2)3=x6,幂的乘方,底数不变指数相乘,故本选项正确;
D、x2+x2=2x2,故本选项错误.
故选:C.
2.实数a在数轴上的对应点位置如图所示,若实数b满足:|b|<a,则b的值可以是( )
A.﹣3 B.﹣2 C.3 D.4
【分析】直接利用数轴得出a的取值范围,再结合绝对值的性质得出b的值.
解:由数轴可得:2<a<3,
∵|b|<a,
∴b的值可以是:﹣2.
故选:B.
3.在一个样本中,50个数据分别落在5个小组内,第1、2、3、5小组数据的个数分别是2、8、15、5,则第4小组的频率是( )
A.0.6 B.20 C.0.4 D.30
【分析】根据总数计算出第4小组的频数,用第4小组的频数除以数据总数就是第4小组的频率.
解:第4小组的频数:50﹣2﹣8﹣15﹣5=20,
第4小组的频率为:20÷50=0.4.
∴第4小组的频率为0.4.
故选:C.
4.已知y=++9,则y+x的平方根是( )
A.3 B.±3 C.4 D.±4
【分析】直接利用二次根式有意义的条件得出x的值,进而得出y的值,再利用平方根的定义得出答案.
解:由题意可得:,
解得:x=7,
故y=9,
则y+x=9+7=16,
故y+x的平方根是:±4.
故选:D.
5.若分式有意义,则x的取值范围是( )
A.x≠2 B.x≠﹣2 C.x≠4 D.x≠﹣4
【分析】根据分式有意义的条件即可得出答案.
解:∵2x+4≠0,
∴x≠﹣2,
故选:B.
6.如果把分式中的x,y同时变为原来的4倍,那么该分式的值( )
A.不变 B.变为原来的4倍
C.变为原来的 D.变为原来的
【分析】根据题意可得== ,即可求解.
解:x,y同时变为原来的4倍,
则有== ,
∴该分式的值是原分式值的,
故选:D.
7.如图,在△ABC中,∠C=90°,AC=16,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,则△ABC的面积为( )
A.16 B.32 C.48 D.64
【分析】根据线段垂直平分线的性质得到AD=BD,根据题意求出AD、CD,根据勾股定理求出BC,根据三角形的面积公式计算,得到答案.
解:∵MN是AB的垂直平分线,
∴AD=BD,
∵CD:DB=3:5,AC=16,
∴AD=BD=10,CD=6,
∴AC=AD+CD=16,
由勾股定理得:BC===8,
则S△ABC=AC BC=×16×8=64,
故选:D.
8.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是( )
A.40° B.45° C.50° D.60°
【分析】先利用AAS判定△BDF≌△ADC,从而得出BD=DA,即△ABD为等腰直角三角形.所以得出∠ABC=45°.
解:∵AD⊥BC于D,BE⊥AC于E,
∴∠BEA=∠ADC=90°.
∵∠FBD+∠BFD=90°,∠AFE+∠FAE=90°,∠BFD=∠AFE,
∴∠FBD=∠FAE,
在△BDF和△ADC中,,
∴△BDF≌△ADC(AAS),
∴BD=AD,
∴∠ABC=∠BAD=45°,
故选:B.
9.如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
【分析】根据角平分线的定义和垂直的定义得到∠ABD=∠EBD=∠ABC=,∠AFB=∠EFB=90°,推出AB=BE,根据等腰三角形的性质得到AF=EF,求得AD=ED,得到∠DAF=∠DEF,根据三角形的外角的性质即可得到结论.
解:∵∠ABC=35°,∠C=50°,
∴∠BAC=180°﹣35°﹣50°=95°,
∵BD是△ABC的角平分线,
∴∠ABF=∠EBF,
∵AE⊥BD,
∴∠AFB=∠EFB=90°,
在△ABF和△EBF中,
,
∴△ABF≌△EBF(ASA),
∴AB=EB,AF=EF,
∴∠BAE=∠BEA,DA=DE,
∴∠DAE=∠DEA,
∴∠BAE+∠DAE=∠BEA+∠DEA,
∴∠DEB=∠DAB=95°,
∴∠CDE=∠DEB﹣∠C=45°,
故选:C.
10.如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=4,S3=12,则S2的值为( )
A.16 B.24 C.48 D.64
【分析】根据已知条件得到AB=2,CD=2,过A作AE∥CD交BC于E,则∠AEB=∠DCB,根据平行四边形的性质得到CE=AD,AE=CD=2,由已知条件得到∠BAE=90°,根据勾股定理得到BE=,于是得到结论.
解:∵S1=4,S3=12,
∴AB=2,CD=2,
过A作AE∥CD交BC于E,
则∠AEB=∠DCB,
∵AD∥BC,
∴四边形AECD是平行四边形,
∴CE=AD,AE=CD=2,
∵∠ABC+∠DCB=90°,
∴∠AEB+∠ABC=90°,
∴∠BAE=90°,
∴BE=,
∵BC=2AD,
∴BC=2BE=8,
∴S2=(8)2=64,
故选:D.
11.矩形ABCD内放入两张边长分别为a和b(a>b)的正方形纸片,按照图①放置,矩形纸片没有被两个正方形覆盖的部分(黑色阴影部分)的面积为S1;按照图②放置,矩形纸片没有被两个正方形覆盖的部分面积为S2;按图③放置,矩形纸片没有被两个正方形覆盖的部分的面积为S3,已知S1﹣S3=3,S2﹣S3=12,设AD﹣AB=m,则下列值是常数的是( )
A.ma B.mb C.m D.a+b
【分析】利用面积的和差表示出S2﹣S1,根据图①与图②分别表示出矩形的面积,进而得到b(AD﹣AB)=12,从而求解.
解:由,
可得:S2﹣S1=9,
由图①得:S矩形ABCD=S1+a2+b(AD﹣a),
由图②得:S矩形ABCD=S2+a2+b(AB﹣a),
∴S1+a2+b(AD﹣a)=S2+a2+b(AB﹣a),
∴S2﹣S1=b(AD﹣AB),
∵AD﹣AB=m,
∴mb=9.
故选:B.
12.如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①DC′平分∠BDE;②BC长为2a+b;③△BDC′是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( )
A.①②④ B.②③④ C.②③ D.②④
【分析】由△ABC为等腰直角三角形,得AB=AC=BC,∠ABC=∠C=45°,根据折叠可得∠C′DE=45°,∠BDC′=∠DC′E﹣∠DBE=22.5°,可判定①错误;而BE=AB=AC=AD+CD=DE+CD=a+b,CE=DE=a,可判定②正确;由∠DBC=∠BDC′=22.5°,可判定③正确;又△CED的周长=DE+EC+DC=2a+b,可判定④正确,即可得到答案.
解:∵△ABC为等腰直角三角形,
∴AB=AC=BC,∠ABC=∠C=45°,
∵Rt△ABD折叠得到Rt△EBD,
∴∠DBE=∠ABC=22.5°,DE=AD=a,∠DEB=90°,
∴△DCE为等腰直角三角形,
∴CE=DE=a,∠CDE=45°,
∵Rt△DC′E由Rt△DCE折叠得到,
∴∠C′DE=∠CDE=45°,∠DC′E=45°,
∴∠BDC′=∠DC′E﹣∠DBE=22.5°,
∴DC′不平分∠BDE,所以①错误;
∵BE=AB=AC=AD+CD=DE+CD=a+b,CE=DE=a,
∴BC=BE+CE=a+b+a=2a+b,所以②正确;
∵∠DBC=∠BDC′=22.5°,
∴△BDC′是等腰三角形,所以③正确;
∵△CED的周长=DE+EC+DC=a+a+b=2a+b,
∴△CED的周长等于BC的长,所以④正确.
故答案为:②③④,
故选:B.
二、填空题(共5小题,满分15分)
13.因式分解:xy2+2xy+x= x(y+1)2 .
【分析】先提取公因式x,再对余下的多项式利用完全平方公式继续分解.
解:xy2+2xy+x,
=x(y2+2y+1),
=x(y+1)2.
故答案为:x(y+1)2.
14.若2m+2m+2m+2m=8,则m= 1 .
【分析】首先合并同类项,再利用同底数幂的乘法的法则进行求解即可.
解:∵2m+2m+2m+2m=8,
∴4×2m=8,
∴22×2m=8,
则有:2m+2=23,
∴m+2=3,
解得:m=1.
故答案为:1.
15.在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为 126或66 cm2.
【分析】此题分两种情况:∠B为锐角或∠B为钝角已知AB、AC的值,利用勾股定理即可求出BC的长,利用三角形的面积公式得结果.
解:当∠B为锐角时(如图1),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=21,
∴S△ABC==×21×12=126cm2;
当∠B为钝角时(如图2),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=CD﹣BD=16﹣5=11cm,
∴S△ABC==×11×12=66cm2,
故答案为:126或66.
16.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.E为线段BD上一点,连结CE,将边BC沿CE折叠,使点B的对称点B'落在CD的延长线上.若AB=10,BC=8,则△ACE的面积为 .
【分析】求出AC=6,面积法求出CD=,在Rt△BCD中,用勾股定理得BD=,即可得B'D=B'C﹣CD=,设BE=B'E=x,则DE=BD﹣BE=﹣x,在Rt△B'DE中,用勾股定理可得BE=4,即可得到答案.
解:∵∠ACB=90°,AB=10,BC=8,
∴AC==6,
∵CD⊥AB,
∴2S△ABC=AB CD=AC BC,
∴CD==,
在Rt△BCD中,BD===,
∵将边BC沿CE折叠,使点B的对称点B'落在CD的延长线上,
∴B'C=BC=8,BE=B'E,
∴B'D=B'C﹣CD=8﹣=,
设BE=B'E=x,则DE=BD﹣BE=﹣x,
在Rt△B'DE中,B'D2+DE2=B'E2,
∴()2+(﹣x)2=x2,
解得x=4,
∴BE=4,
∴AE=AB﹣BE=6,
∴△ACE的面积为AE CD=×6×=,
故答案为:.
17.如图,已知在△ABC中,AB=AC,∠BAC=90,直角∠EPF顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下4个结论:①AE=CF,②△EPF是等腰Rt△,③S四边形AEPF=S△ABC,④EF=AP.当∠EPF在△ABC内部绕顶点P旋转时(点E不与AB重合),上述结论始终成立的是 ①②③ .
【分析】由题意可证△AEP≌△CFP,可得:①AE=CF,②△EPF是等腰Rt△,③S四边形AEPF=S△ABC,即成立的为①②③.
解:∵AB=AC,∠BAC=90,点P是BC的中点
∴AP=BP=CP,∠B=∠C=∠BAP=∠PAC=45°,AP⊥BC,S△APC=S△ABC
∵∠APF+∠CPF=90°,∠APF+∠APE=90°
∴∠APE=∠CPF且AP=PC,∠C=∠BAP
∴△AEP≌△CFP(ASA)
∴AE=CF,PF=PE,S△AEP=S△CFP.
∴△PEF是等腰直角三角形,S△APC=S四边形AEPF.
∴S四边形AEPF=S△ABC
故①②③正确,
∵AP是定值,EF随PF的变化而变化,只有当PF⊥AC时,EF=AP
∴④不正确
故答案为:①②③
三、解答题(共6小题,满分31分)
18.计算:﹣12018+()﹣2++(π﹣2019)0﹣|﹣2|.
【分析】首先计算乘方、开方,然后从左向右依次计算,求出算式的值是多少即可.
解:﹣12018+()﹣2++(π﹣2019)0﹣|﹣2|
=﹣1+4+(﹣3)+1﹣2+
=﹣1+
19.已知(x+y)2=1,(x﹣y)2=49,求x2+y2与xy的值.
【分析】已知等式利用完全平方公式化简,相加减即可求出所求式子的值.
解:∵(x+y)2=x2+y2+2xy=1①,(x﹣y)2=x2+y2﹣2xy=49②,
∴①+②得:2(x2+y2)=50,即x2+y2=25;
①﹣②得:4xy=﹣48,即xy=﹣12.
20.已知a=,b=,求代数式[(ab+1)(ab﹣2)﹣2a2b2+2]÷(﹣ab)的值.
【分析】先根据多项式乘多项式算括号里面的,合并同类项,算除法,最后代入求出答案即可.
解:[(ab+1)(ab﹣2)﹣2a2b2+2]÷(﹣ab)
=(a2b2﹣ab﹣2﹣2a2b2+2)÷(﹣ab)
=(﹣a2b2﹣ab)÷(﹣ab)
=ab+1,
当a=,b=时,
原式=×+1
=2+1
=3.
21.本学期,我校开设了“防疫宣传”“心理疏导”等课程,为了解学生对新开设课程的掌握情况,从八年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了两幅不完整的统计图.根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 40 名;
(2)扇形统计图中表示A级的扇形圆心角α的度数是 54° ,并把条形统计图补充完整;
(3)该校八年级共有学生1200名,如果全部参加这次测试,估计优秀的人数为多少?
【分析】(1)根据B级的人数和所占的百分比,可以求得本次抽样测试的学生人数;
(2)根据条形统计图中的数据,可以计算出扇形统计图中表示A级的扇形圆心角α的度数和C级的人数,即可将条形统计图补充完整;
(3)用总人数乘以优秀的人数所占的百分比即可.
解:(1)本次抽样测试的学生人数是:12÷30%=40(名),
故答案为:40;
(2)扇形统计图中表示A级的扇形圆心角α的度数是:360°×=54°,
C级的人数为:40×35%=14,补充完整的条形统计图如图所示:
故答案为:54°;
(3)1200×=180(人),
答:估计优秀的人数为180人.
22.利用平面图形中面积相等的等量关系可以得到某些数学公式.例如:根据图①,
我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.
(1)根据图②,可以得到的数学公式是 (a﹣b)2=a2﹣2ab+b2 ;
(2)根据图③,请写出(a+b)、(a﹣b)、ab的等量关系是 (a+b)2=(a﹣b)2+4ab .
(3)根据图④,请写出一个等式: (a+b+c)2=a2+b2+c2+2ab+2bc+2ca ;
(4)小明同学使用图⑤中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片,恰好拼成一个面积为(3a+b)(a+3b)的长方形,则可得x+y+z的值为 16 ;
(5)类似地,利用立体图形体积的等量关系也可以得到某些数学公式.现请你根据图⑥,写出一个等式: (a+b)3=a3+3a2b+3ab2+b3 .
【分析】(1)根据图②利用图形间面积的和差关系可以表示出此题结果;
(2)从整体和部分求和两个角度分别表示出图③中正方形的面积即可;
(3)从整体和部分求和两个角度分别表示出图④中正方形的面积即可;,
(4)由计算(3a+b)(a+3b)可得x、y、z的值,就可以求得此题的结果;
(4)从整体和部分求和两个角度分别表示出图⑥中正方体的体积.
【解答】(1)图②中左上角正方形的面积可表示为(a﹣b)2或a2﹣2ab+b2,
故答案为:(a﹣b)2=a2﹣2ab+b2;
(2)用两种方法表示图③的面积分别为:(a+b)2和(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab.
(3)用两种方法表示图④的面积分别为:(a+b+c)2和a2+b2+c2+2ab+2bc+2ca,
故答案为:(a+b+c)2=a2+b2+c2+2ab+2bc+2ca;
(4)∵(3a+b)(a+3b)=3a2+9ab+ab+3b2=3a2+10ab+3b2,
∴x=3,y=10,z=3,
∴x+y+z=3+10+3=16,
故答案为:16;
(5)图⑥的体积可表示为(a+b)3或a3+3a2b+3ab2+b3,
故答案为:(a+b)3=a3+3a2b+3ab2+b3.
23.如图,四边形ABCD中,∠B=∠C,P是线段BC上一点,PA=PD,且∠APD=90°.
(1)如图1,若∠B=∠C=90°,求证:AB+CD=BC;
(2)如图1,若∠B=∠C=90°,问AB2、CD2、AD2之间有怎样的数量关系,请写出你的猜想,并给予证明;
(3)如图2,若∠B=∠C=45°,且PB=PC,问AB2、CD2、AD2之间有怎样的数量关系,请直接写出你的猜想即可,不需要证明.
【分析】(1)证明△ABP≌△PCD(AAS),推出AB=PC,PB=CD,可得结论.
(2)猜想:AB2+CD2=AD2.利用等腰直角三角形的性质以及勾股定理,可得结论;
(3)结论:AB2+CD2=AD2.如图2中,过点A作AN⊥BC由点N,过点D作DM⊥BC由点M.利用(2)中结论以及等腰直角三角形的性质解决问题即可.
【解答】(1)证明:如图1中,
∵∠B=∠C=∠APD=90°,
∴∠APB+∠PAB=90°,∠APB+∠DPC=90°,
∴∠BAP=∠DPC,
在△ABP和△PCD中,
,
∴△ABP≌△PCD(AAS),
∴AB=PC,PB=CD,
∴AB+CD=PC+PB=BC;
(2)猜想:AB2+CD2=AD2.
理由:在Rt△APD中,∵PA=PD,∠APD=90°,
∴AD2=PA2+PD2,
∴PD2=AD2,
在Rt△DCP中,PD2=PC2+CD2,
∵AB=CP,
∴AB2+CD2=AD2;
(3)结论:AB2+CD2=AD2.
理由:如图2中,过点A作AN⊥BC由点N,过点D作DM⊥BC由点M.
∵∠B=∠C=45°,∠ANB=∠DMC=90°,
∴△ABN,△DMC都是等腰直角三角形,
∴AB2=2AN2,CD2=2DM2,
由(2)可知,AN2+DM2=AD2,
∴2AN2+2DM2=AD2,
∴AB2+CD2=AD2.
一、选择题
1.下列运算正确的是( )
A.x x2=x2 B.(xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
2.实数a在数轴上的对应点位置如图所示,若实数b满足:|b|<a,则b的值可以是( )
A.﹣3 B.﹣2 C.3 D.4
3.在一个样本中,50个数据分别落在5个小组内,第1、2、3、5小组数据的个数分别是2、8、15、5,则第4小组的频率是( )
A.0.6 B.20 C.0.4 D.30
4.已知y=++9,则y+x的平方根是( )
A.3 B.±3 C.4 D.±4
5.若分式有意义,则x的取值范围是( )
A.x≠2 B.x≠﹣2 C.x≠4 D.x≠﹣4
6.如果把分式中的x,y同时变为原来的4倍,那么该分式的值( )
A.不变 B.变为原来的4倍
C.变为原来的 D.变为原来的
7.如图,在△ABC中,∠C=90°,AC=16,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,则△ABC的面积为( )
A.16 B.32 C.48 D.64
8.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是( )
A.40° B.45° C.50° D.60°
9.如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
10.如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=4,S3=12,则S2的值为( )
A.16 B.24 C.48 D.64
11.矩形ABCD内放入两张边长分别为a和b(a>b)的正方形纸片,按照图①放置,矩形纸片没有被两个正方形覆盖的部分(黑色阴影部分)的面积为S1;按照图②放置,矩形纸片没有被两个正方形覆盖的部分面积为S2;按图③放置,矩形纸片没有被两个正方形覆盖的部分的面积为S3,已知S1﹣S3=3,S2﹣S3=12,设AD﹣AB=m,则下列值是常数的是( )
A.ma B.mb C.m D.a+b
12.如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①DC′平分∠BDE;②BC长为2a+b;③△BDC′是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( )
A.①②④ B.②③④ C.②③ D.②④
二、填空题(共5小题,满分15分)
13.因式分解:xy2+2xy+x= .
14.若2m+2m+2m+2m=8,则m= .
15.在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为 cm2.
16.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.E为线段BD上一点,连结CE,将边BC沿CE折叠,使点B的对称点B'落在CD的延长线上.若AB=10,BC=8,则△ACE的面积为 .
17.如图,已知在△ABC中,AB=AC,∠BAC=90,直角∠EPF顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下4个结论:①AE=CF,②△EPF是等腰Rt△,③S四边形AEPF=S△ABC,④EF=AP.当∠EPF在△ABC内部绕顶点P旋转时(点E不与AB重合),上述结论始终成立的是 .
三、解答题(共6小题,满分31分)
18.计算:﹣12018+()﹣2++(π﹣2019)0﹣|﹣2|.
19.已知(x+y)2=1,(x﹣y)2=49,求x2+y2与xy的值.
20.已知a=,b=,求代数式[(ab+1)(ab﹣2)﹣2a2b2+2]÷(﹣ab)的值.
21.本学期,我校开设了“防疫宣传”“心理疏导”等课程,为了解学生对新开设课程的掌握情况,从八年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了两幅不完整的统计图.根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 名;
(2)扇形统计图中表示A级的扇形圆心角α的度数是 ,并把条形统计图补充完整;
(3)该校八年级共有学生1200名,如果全部参加这次测试,估计优秀的人数为多少?
22.利用平面图形中面积相等的等量关系可以得到某些数学公式.例如:根据图①,
我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.
(1)根据图②,可以得到的数学公式是 ;
(2)根据图③,请写出(a+b)、(a﹣b)、ab的等量关系是 .
(3)根据图④,请写出一个等式: ;
(4)小明同学使用图⑤中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片,恰好拼成一个面积为(3a+b)(a+3b)的长方形,则可得x+y+z的值为 ;
(5)类似地,利用立体图形体积的等量关系也可以得到某些数学公式.现请你根据图⑥,写出一个等式: .
23.如图,四边形ABCD中,∠B=∠C,P是线段BC上一点,PA=PD,且∠APD=90°.
(1)如图1,若∠B=∠C=90°,求证:AB+CD=BC;
(2)如图1,若∠B=∠C=90°,问AB2、CD2、AD2之间有怎样的数量关系,请写出你的猜想,并给予证明;
(3)如图2,若∠B=∠C=45°,且PB=PC,问AB2、CD2、AD2之间有怎样的数量关系,请直接写出你的猜想即可,不需要证明.
参考答案
一、选择
1.下列运算正确的是( )
A.x x2=x2 B.(xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
【分析】根据同底数幂的除法,底数不变指数相减,合并同类项,系数相加字母和字母的指数不变,同底数幂的乘法,底数不变指数相加,幂的乘方,底数不变指数相乘,对各选项计算后利用排除法求解.
解:A、x x2=x3同底数幂的乘法,底数不变指数相加,故本选项错误;
B、(xy)2=x2y2,幂的乘方,底数不变指数相乘,故本选项错误;
C、(x2)3=x6,幂的乘方,底数不变指数相乘,故本选项正确;
D、x2+x2=2x2,故本选项错误.
故选:C.
2.实数a在数轴上的对应点位置如图所示,若实数b满足:|b|<a,则b的值可以是( )
A.﹣3 B.﹣2 C.3 D.4
【分析】直接利用数轴得出a的取值范围,再结合绝对值的性质得出b的值.
解:由数轴可得:2<a<3,
∵|b|<a,
∴b的值可以是:﹣2.
故选:B.
3.在一个样本中,50个数据分别落在5个小组内,第1、2、3、5小组数据的个数分别是2、8、15、5,则第4小组的频率是( )
A.0.6 B.20 C.0.4 D.30
【分析】根据总数计算出第4小组的频数,用第4小组的频数除以数据总数就是第4小组的频率.
解:第4小组的频数:50﹣2﹣8﹣15﹣5=20,
第4小组的频率为:20÷50=0.4.
∴第4小组的频率为0.4.
故选:C.
4.已知y=++9,则y+x的平方根是( )
A.3 B.±3 C.4 D.±4
【分析】直接利用二次根式有意义的条件得出x的值,进而得出y的值,再利用平方根的定义得出答案.
解:由题意可得:,
解得:x=7,
故y=9,
则y+x=9+7=16,
故y+x的平方根是:±4.
故选:D.
5.若分式有意义,则x的取值范围是( )
A.x≠2 B.x≠﹣2 C.x≠4 D.x≠﹣4
【分析】根据分式有意义的条件即可得出答案.
解:∵2x+4≠0,
∴x≠﹣2,
故选:B.
6.如果把分式中的x,y同时变为原来的4倍,那么该分式的值( )
A.不变 B.变为原来的4倍
C.变为原来的 D.变为原来的
【分析】根据题意可得== ,即可求解.
解:x,y同时变为原来的4倍,
则有== ,
∴该分式的值是原分式值的,
故选:D.
7.如图,在△ABC中,∠C=90°,AC=16,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,则△ABC的面积为( )
A.16 B.32 C.48 D.64
【分析】根据线段垂直平分线的性质得到AD=BD,根据题意求出AD、CD,根据勾股定理求出BC,根据三角形的面积公式计算,得到答案.
解:∵MN是AB的垂直平分线,
∴AD=BD,
∵CD:DB=3:5,AC=16,
∴AD=BD=10,CD=6,
∴AC=AD+CD=16,
由勾股定理得:BC===8,
则S△ABC=AC BC=×16×8=64,
故选:D.
8.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是( )
A.40° B.45° C.50° D.60°
【分析】先利用AAS判定△BDF≌△ADC,从而得出BD=DA,即△ABD为等腰直角三角形.所以得出∠ABC=45°.
解:∵AD⊥BC于D,BE⊥AC于E,
∴∠BEA=∠ADC=90°.
∵∠FBD+∠BFD=90°,∠AFE+∠FAE=90°,∠BFD=∠AFE,
∴∠FBD=∠FAE,
在△BDF和△ADC中,,
∴△BDF≌△ADC(AAS),
∴BD=AD,
∴∠ABC=∠BAD=45°,
故选:B.
9.如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
【分析】根据角平分线的定义和垂直的定义得到∠ABD=∠EBD=∠ABC=,∠AFB=∠EFB=90°,推出AB=BE,根据等腰三角形的性质得到AF=EF,求得AD=ED,得到∠DAF=∠DEF,根据三角形的外角的性质即可得到结论.
解:∵∠ABC=35°,∠C=50°,
∴∠BAC=180°﹣35°﹣50°=95°,
∵BD是△ABC的角平分线,
∴∠ABF=∠EBF,
∵AE⊥BD,
∴∠AFB=∠EFB=90°,
在△ABF和△EBF中,
,
∴△ABF≌△EBF(ASA),
∴AB=EB,AF=EF,
∴∠BAE=∠BEA,DA=DE,
∴∠DAE=∠DEA,
∴∠BAE+∠DAE=∠BEA+∠DEA,
∴∠DEB=∠DAB=95°,
∴∠CDE=∠DEB﹣∠C=45°,
故选:C.
10.如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=4,S3=12,则S2的值为( )
A.16 B.24 C.48 D.64
【分析】根据已知条件得到AB=2,CD=2,过A作AE∥CD交BC于E,则∠AEB=∠DCB,根据平行四边形的性质得到CE=AD,AE=CD=2,由已知条件得到∠BAE=90°,根据勾股定理得到BE=,于是得到结论.
解:∵S1=4,S3=12,
∴AB=2,CD=2,
过A作AE∥CD交BC于E,
则∠AEB=∠DCB,
∵AD∥BC,
∴四边形AECD是平行四边形,
∴CE=AD,AE=CD=2,
∵∠ABC+∠DCB=90°,
∴∠AEB+∠ABC=90°,
∴∠BAE=90°,
∴BE=,
∵BC=2AD,
∴BC=2BE=8,
∴S2=(8)2=64,
故选:D.
11.矩形ABCD内放入两张边长分别为a和b(a>b)的正方形纸片,按照图①放置,矩形纸片没有被两个正方形覆盖的部分(黑色阴影部分)的面积为S1;按照图②放置,矩形纸片没有被两个正方形覆盖的部分面积为S2;按图③放置,矩形纸片没有被两个正方形覆盖的部分的面积为S3,已知S1﹣S3=3,S2﹣S3=12,设AD﹣AB=m,则下列值是常数的是( )
A.ma B.mb C.m D.a+b
【分析】利用面积的和差表示出S2﹣S1,根据图①与图②分别表示出矩形的面积,进而得到b(AD﹣AB)=12,从而求解.
解:由,
可得:S2﹣S1=9,
由图①得:S矩形ABCD=S1+a2+b(AD﹣a),
由图②得:S矩形ABCD=S2+a2+b(AB﹣a),
∴S1+a2+b(AD﹣a)=S2+a2+b(AB﹣a),
∴S2﹣S1=b(AD﹣AB),
∵AD﹣AB=m,
∴mb=9.
故选:B.
12.如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①DC′平分∠BDE;②BC长为2a+b;③△BDC′是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( )
A.①②④ B.②③④ C.②③ D.②④
【分析】由△ABC为等腰直角三角形,得AB=AC=BC,∠ABC=∠C=45°,根据折叠可得∠C′DE=45°,∠BDC′=∠DC′E﹣∠DBE=22.5°,可判定①错误;而BE=AB=AC=AD+CD=DE+CD=a+b,CE=DE=a,可判定②正确;由∠DBC=∠BDC′=22.5°,可判定③正确;又△CED的周长=DE+EC+DC=2a+b,可判定④正确,即可得到答案.
解:∵△ABC为等腰直角三角形,
∴AB=AC=BC,∠ABC=∠C=45°,
∵Rt△ABD折叠得到Rt△EBD,
∴∠DBE=∠ABC=22.5°,DE=AD=a,∠DEB=90°,
∴△DCE为等腰直角三角形,
∴CE=DE=a,∠CDE=45°,
∵Rt△DC′E由Rt△DCE折叠得到,
∴∠C′DE=∠CDE=45°,∠DC′E=45°,
∴∠BDC′=∠DC′E﹣∠DBE=22.5°,
∴DC′不平分∠BDE,所以①错误;
∵BE=AB=AC=AD+CD=DE+CD=a+b,CE=DE=a,
∴BC=BE+CE=a+b+a=2a+b,所以②正确;
∵∠DBC=∠BDC′=22.5°,
∴△BDC′是等腰三角形,所以③正确;
∵△CED的周长=DE+EC+DC=a+a+b=2a+b,
∴△CED的周长等于BC的长,所以④正确.
故答案为:②③④,
故选:B.
二、填空题(共5小题,满分15分)
13.因式分解:xy2+2xy+x= x(y+1)2 .
【分析】先提取公因式x,再对余下的多项式利用完全平方公式继续分解.
解:xy2+2xy+x,
=x(y2+2y+1),
=x(y+1)2.
故答案为:x(y+1)2.
14.若2m+2m+2m+2m=8,则m= 1 .
【分析】首先合并同类项,再利用同底数幂的乘法的法则进行求解即可.
解:∵2m+2m+2m+2m=8,
∴4×2m=8,
∴22×2m=8,
则有:2m+2=23,
∴m+2=3,
解得:m=1.
故答案为:1.
15.在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为 126或66 cm2.
【分析】此题分两种情况:∠B为锐角或∠B为钝角已知AB、AC的值,利用勾股定理即可求出BC的长,利用三角形的面积公式得结果.
解:当∠B为锐角时(如图1),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=21,
∴S△ABC==×21×12=126cm2;
当∠B为钝角时(如图2),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=CD﹣BD=16﹣5=11cm,
∴S△ABC==×11×12=66cm2,
故答案为:126或66.
16.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.E为线段BD上一点,连结CE,将边BC沿CE折叠,使点B的对称点B'落在CD的延长线上.若AB=10,BC=8,则△ACE的面积为 .
【分析】求出AC=6,面积法求出CD=,在Rt△BCD中,用勾股定理得BD=,即可得B'D=B'C﹣CD=,设BE=B'E=x,则DE=BD﹣BE=﹣x,在Rt△B'DE中,用勾股定理可得BE=4,即可得到答案.
解:∵∠ACB=90°,AB=10,BC=8,
∴AC==6,
∵CD⊥AB,
∴2S△ABC=AB CD=AC BC,
∴CD==,
在Rt△BCD中,BD===,
∵将边BC沿CE折叠,使点B的对称点B'落在CD的延长线上,
∴B'C=BC=8,BE=B'E,
∴B'D=B'C﹣CD=8﹣=,
设BE=B'E=x,则DE=BD﹣BE=﹣x,
在Rt△B'DE中,B'D2+DE2=B'E2,
∴()2+(﹣x)2=x2,
解得x=4,
∴BE=4,
∴AE=AB﹣BE=6,
∴△ACE的面积为AE CD=×6×=,
故答案为:.
17.如图,已知在△ABC中,AB=AC,∠BAC=90,直角∠EPF顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下4个结论:①AE=CF,②△EPF是等腰Rt△,③S四边形AEPF=S△ABC,④EF=AP.当∠EPF在△ABC内部绕顶点P旋转时(点E不与AB重合),上述结论始终成立的是 ①②③ .
【分析】由题意可证△AEP≌△CFP,可得:①AE=CF,②△EPF是等腰Rt△,③S四边形AEPF=S△ABC,即成立的为①②③.
解:∵AB=AC,∠BAC=90,点P是BC的中点
∴AP=BP=CP,∠B=∠C=∠BAP=∠PAC=45°,AP⊥BC,S△APC=S△ABC
∵∠APF+∠CPF=90°,∠APF+∠APE=90°
∴∠APE=∠CPF且AP=PC,∠C=∠BAP
∴△AEP≌△CFP(ASA)
∴AE=CF,PF=PE,S△AEP=S△CFP.
∴△PEF是等腰直角三角形,S△APC=S四边形AEPF.
∴S四边形AEPF=S△ABC
故①②③正确,
∵AP是定值,EF随PF的变化而变化,只有当PF⊥AC时,EF=AP
∴④不正确
故答案为:①②③
三、解答题(共6小题,满分31分)
18.计算:﹣12018+()﹣2++(π﹣2019)0﹣|﹣2|.
【分析】首先计算乘方、开方,然后从左向右依次计算,求出算式的值是多少即可.
解:﹣12018+()﹣2++(π﹣2019)0﹣|﹣2|
=﹣1+4+(﹣3)+1﹣2+
=﹣1+
19.已知(x+y)2=1,(x﹣y)2=49,求x2+y2与xy的值.
【分析】已知等式利用完全平方公式化简,相加减即可求出所求式子的值.
解:∵(x+y)2=x2+y2+2xy=1①,(x﹣y)2=x2+y2﹣2xy=49②,
∴①+②得:2(x2+y2)=50,即x2+y2=25;
①﹣②得:4xy=﹣48,即xy=﹣12.
20.已知a=,b=,求代数式[(ab+1)(ab﹣2)﹣2a2b2+2]÷(﹣ab)的值.
【分析】先根据多项式乘多项式算括号里面的,合并同类项,算除法,最后代入求出答案即可.
解:[(ab+1)(ab﹣2)﹣2a2b2+2]÷(﹣ab)
=(a2b2﹣ab﹣2﹣2a2b2+2)÷(﹣ab)
=(﹣a2b2﹣ab)÷(﹣ab)
=ab+1,
当a=,b=时,
原式=×+1
=2+1
=3.
21.本学期,我校开设了“防疫宣传”“心理疏导”等课程,为了解学生对新开设课程的掌握情况,从八年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了两幅不完整的统计图.根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 40 名;
(2)扇形统计图中表示A级的扇形圆心角α的度数是 54° ,并把条形统计图补充完整;
(3)该校八年级共有学生1200名,如果全部参加这次测试,估计优秀的人数为多少?
【分析】(1)根据B级的人数和所占的百分比,可以求得本次抽样测试的学生人数;
(2)根据条形统计图中的数据,可以计算出扇形统计图中表示A级的扇形圆心角α的度数和C级的人数,即可将条形统计图补充完整;
(3)用总人数乘以优秀的人数所占的百分比即可.
解:(1)本次抽样测试的学生人数是:12÷30%=40(名),
故答案为:40;
(2)扇形统计图中表示A级的扇形圆心角α的度数是:360°×=54°,
C级的人数为:40×35%=14,补充完整的条形统计图如图所示:
故答案为:54°;
(3)1200×=180(人),
答:估计优秀的人数为180人.
22.利用平面图形中面积相等的等量关系可以得到某些数学公式.例如:根据图①,
我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.
(1)根据图②,可以得到的数学公式是 (a﹣b)2=a2﹣2ab+b2 ;
(2)根据图③,请写出(a+b)、(a﹣b)、ab的等量关系是 (a+b)2=(a﹣b)2+4ab .
(3)根据图④,请写出一个等式: (a+b+c)2=a2+b2+c2+2ab+2bc+2ca ;
(4)小明同学使用图⑤中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片,恰好拼成一个面积为(3a+b)(a+3b)的长方形,则可得x+y+z的值为 16 ;
(5)类似地,利用立体图形体积的等量关系也可以得到某些数学公式.现请你根据图⑥,写出一个等式: (a+b)3=a3+3a2b+3ab2+b3 .
【分析】(1)根据图②利用图形间面积的和差关系可以表示出此题结果;
(2)从整体和部分求和两个角度分别表示出图③中正方形的面积即可;
(3)从整体和部分求和两个角度分别表示出图④中正方形的面积即可;,
(4)由计算(3a+b)(a+3b)可得x、y、z的值,就可以求得此题的结果;
(4)从整体和部分求和两个角度分别表示出图⑥中正方体的体积.
【解答】(1)图②中左上角正方形的面积可表示为(a﹣b)2或a2﹣2ab+b2,
故答案为:(a﹣b)2=a2﹣2ab+b2;
(2)用两种方法表示图③的面积分别为:(a+b)2和(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab.
(3)用两种方法表示图④的面积分别为:(a+b+c)2和a2+b2+c2+2ab+2bc+2ca,
故答案为:(a+b+c)2=a2+b2+c2+2ab+2bc+2ca;
(4)∵(3a+b)(a+3b)=3a2+9ab+ab+3b2=3a2+10ab+3b2,
∴x=3,y=10,z=3,
∴x+y+z=3+10+3=16,
故答案为:16;
(5)图⑥的体积可表示为(a+b)3或a3+3a2b+3ab2+b3,
故答案为:(a+b)3=a3+3a2b+3ab2+b3.
23.如图,四边形ABCD中,∠B=∠C,P是线段BC上一点,PA=PD,且∠APD=90°.
(1)如图1,若∠B=∠C=90°,求证:AB+CD=BC;
(2)如图1,若∠B=∠C=90°,问AB2、CD2、AD2之间有怎样的数量关系,请写出你的猜想,并给予证明;
(3)如图2,若∠B=∠C=45°,且PB=PC,问AB2、CD2、AD2之间有怎样的数量关系,请直接写出你的猜想即可,不需要证明.
【分析】(1)证明△ABP≌△PCD(AAS),推出AB=PC,PB=CD,可得结论.
(2)猜想:AB2+CD2=AD2.利用等腰直角三角形的性质以及勾股定理,可得结论;
(3)结论:AB2+CD2=AD2.如图2中,过点A作AN⊥BC由点N,过点D作DM⊥BC由点M.利用(2)中结论以及等腰直角三角形的性质解决问题即可.
【解答】(1)证明:如图1中,
∵∠B=∠C=∠APD=90°,
∴∠APB+∠PAB=90°,∠APB+∠DPC=90°,
∴∠BAP=∠DPC,
在△ABP和△PCD中,
,
∴△ABP≌△PCD(AAS),
∴AB=PC,PB=CD,
∴AB+CD=PC+PB=BC;
(2)猜想:AB2+CD2=AD2.
理由:在Rt△APD中,∵PA=PD,∠APD=90°,
∴AD2=PA2+PD2,
∴PD2=AD2,
在Rt△DCP中,PD2=PC2+CD2,
∵AB=CP,
∴AB2+CD2=AD2;
(3)结论:AB2+CD2=AD2.
理由:如图2中,过点A作AN⊥BC由点N,过点D作DM⊥BC由点M.
∵∠B=∠C=45°,∠ANB=∠DMC=90°,
∴△ABN,△DMC都是等腰直角三角形,
∴AB2=2AN2,CD2=2DM2,
由(2)可知,AN2+DM2=AD2,
∴2AN2+2DM2=AD2,
∴AB2+CD2=AD2.
同课章节目录
