2021-2022学年山东省烟台市招远市八年级(上)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年山东省烟台市招远市八年级(上)期末数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 975.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 00:00:00 | ||
图片预览




文档简介
2021-2022学年山东省烟台市招远市八年级第一学期期末数学试卷(五四学制)
一.选择题。(本大题共12个小题,每小题3分,满分36分)
1.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.一棋谱中四部分的截图由黑白棋子摆成的图案是中心对称的是( )
A. B. C. D.
2.已知四边形ABCD的对角线AC,BD相交于点O,OB=OD.则下列条件中不能判定四边形ABCD为平行四边形的是( )
A.OA=OC B.AB∥CD C.AD∥BC D.AB=CD
3.若式子+有意义,则x满足的条件是( )
A.x≠3且x≠﹣3 B.x≠3且x≠4 C.x≠4且x≠﹣5 D.x≠﹣3且x≠﹣5
4.如图,将 ABCD的一边BC延长至点E,若∠A=∠D+50°,则∠B等于( )
A.50° B.65° C.70° D.75°
5.下列说法中错误的是( )
A.一组数据的平均数受极端值的影响较大
B.一组数据的平均数、众数、中位数有可能相同
C.如果一组数据的众数是5,那么这组数据中出现次数最多的数据是5
D.一组数据的中位数有时有两个
6.下列各式,从左到右变形正确的是( )
A.
B.
C.
D.
7.已知3a=3b﹣5,则代数式3a2﹣6ab+3b2﹣3的值为( )
A. B.2 C.22 D.
8.如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE⊥DE,则△BDC通过下列变换能与△ACE重合的是( )
A.绕点C逆时针旋转90度
B.沿AB的垂直平分线翻折
C.绕AB的中点M顺时针旋转90度
D.沿DE方向平移
9.已知一组数据的方差s2=[(3﹣7)2+(8﹣7)2+(11﹣7)2+(a﹣7)2+(b﹣7)2+(c﹣7)2],则a+b+c的值为( )
A.22 B.21 C.20 D.7
10.如图,在△ABC中,∠BAC=126°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'刚好落在BC边上,且AB'=CB',则∠C'的度数为( )
A.18° B.16° C.15° D.14°
11.如图,点A的坐标为(1,4),点B在x轴上,把△AOB沿x轴向右平移到△CED,若四边形ABDC的面积为8,则点C的坐标为( )
A.( 2,4) B.(3,4) C.(3,3) D.(4,3)
12.如图,在四边形ABCD中,AB∥CD,BC∥AD,且AD=DC,则下列说法:
①四边形ABCD是平行四边形;
②AB=BC;
③AC⊥BD
④AC平分∠BAD;
⑤若AC=6,BD=8,则四边形ABCD的面积为24.
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
二.填空题。(本大题共6个小题,每小题3分,满分18分)
13.过多边形的一个顶点可做7条对角线,则多边形的内角和为 .
14.如图,将直角△ABC沿斜边AC的方向平移到△DEF的位置,DE交BC于点G,BG=4,EF=10,则线段GC的长 .
15.若x2﹣5x=﹣5,则x+= .
16.如图,将△ABC绕点A逆时针旋转50°得到△ADE.若∠E=65°,且AD⊥BC于点F,则∠BAC的度数为 .
17.定义一种法则“*”如下:a*b=,例如:1*2=,若m*3=,则m的值为 .
18.如图,在平行四边形 ABCD中,AB=3,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 .
三.解答题。(本大题共7个小题,共66分。请在答题卡指定区域内作答.)
19.(1)化简求值:
(﹣)÷,任取一个合适的x的值,求出该代数式的值;
(2)解分式方程:
+3=.
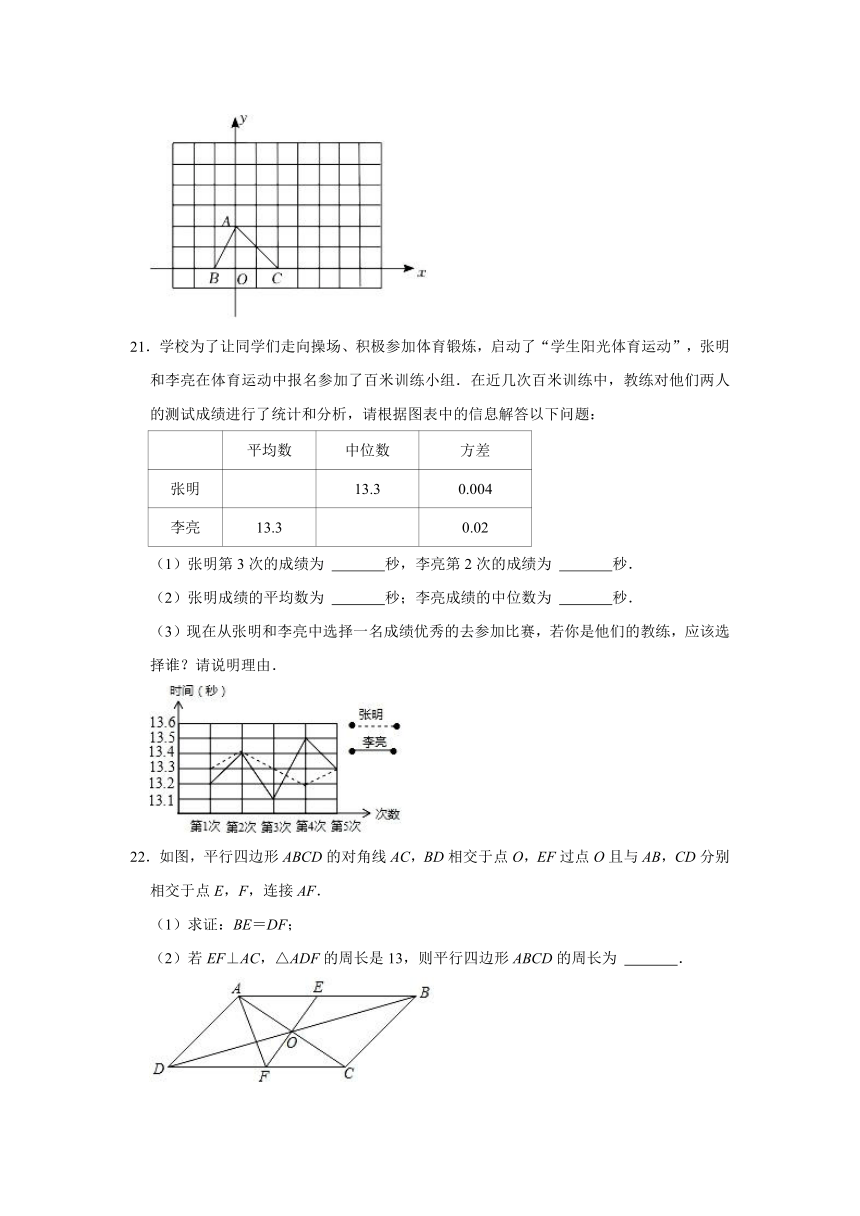
20.如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,2),B(﹣1,0),C(2,0).
(1)△ABC平移后,其中点C的坐标移到点C1(4,1),请在给定的坐标系中画出△A1B1C1.
(2)把△A1B1C1绕着点A1逆时针方向旋转90°,画出旋转后的△A1B2C2.
21.学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明 13.3 0.004
李亮 13.3 0.02
(1)张明第3次的成绩为 秒,李亮第2次的成绩为 秒.
(2)张明成绩的平均数为 秒;李亮成绩的中位数为 秒.
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
22.如图,平行四边形ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F,连接AF.
(1)求证:BE=DF;
(2)若EF⊥AC,△ADF的周长是13,则平行四边形ABCD的周长为 .
23.随着智能分拣设备在快递业务中的普及,快件分拣效率大幅提高.使用某品牌智能分拣设备,每人每小时分拣的快件量是传统分拣方式的25倍,经过测试,由5人用此设备分拣6000件快件的时间,比20人用传统方式分拣同样数量的快件节省3小时.
(1)使用智能分拣设备后,每人每小时可分拣快件多少件?
(2)已知某快递中转站平均每天需要分拣10万件快件,每天工作时间为8小时,如果使用此智能分拣设备,每天只需要安排多少名工人就可以完成分拣工作?
24.请阅读下列材料:
我们可以通过以下方法求代数式x2+6x+5的最小值.
x2+6x+5=x2+2 x 3+32﹣32+5=(x+3)2﹣4;
∵(x+3)2≥0;
∴当x=﹣3时,代数式x2+6x+5的最小值为﹣4.
请根据上述的方法,解答下列问题:
(1)x2+6x﹣1=(x+m)2+n,则mn的值为 .
(2)求代数式的最大值.
(3)若代数式2x2+kx+6的最小值为2,求k的值.
25.已知,△ABC、△ADE是等腰三角形,AB=AC,AD=AE,D是BC上一点,∠DAE=∠BAC,过点E作BC的平行线交AB于点F,连接CF.
(1)如图1,求证:四边形CDEF是平行四边形;
(2)如图2,连接BE、DF,若AD⊥BC,在不添加任何辅助线的情况下,请直接写出图2中长度等于BC的长的的线段.
参考答案
一.选择题。(本大题共12个小题,每小题3分,满分36分)
1.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.一棋谱中四部分的截图由黑白棋子摆成的图案是中心对称的是( )
A. B. C. D.
【分析】把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,根据中心对称图形的概念求解.
解:选项A能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形;
选项B、C、D不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形;
故选:A.
2.已知四边形ABCD的对角线AC,BD相交于点O,OB=OD.则下列条件中不能判定四边形ABCD为平行四边形的是( )
A.OA=OC B.AB∥CD C.AD∥BC D.AB=CD
【分析】根据平行四边形的判定定理分别进行分析即可.
解:A、∵OA=OC,OB=OD,∴四边形ABCD是平行四边形,不符合题意;
B、∵AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠ODC,
∵OB=OD,
∴△ABO≌△DCO(AAS),
∴AB=CD,
∴四边形ABCD是平行四边形,不符合题意;
C、∵AD∥BC,
∴∠OBC=∠ODA,∠OCB=∠OAD,
∵OB=OD,
∴△OBC≌△ODC(AAS),
∴AD=BC,
∴四边形ABCD是平行四边形,不符合题意;
D、∵AB=CD,OB=OD,不能判断四边形ABCD是平行四边形,符合题意;
故选:D.
3.若式子+有意义,则x满足的条件是( )
A.x≠3且x≠﹣3 B.x≠3且x≠4 C.x≠4且x≠﹣5 D.x≠﹣3且x≠﹣5
【分析】直接利用分式有意义的条件得出答案.
解:∵分式有意义,
∴x﹣3≠0,x﹣4≠0,
∴x≠3且x≠4,
故选:B.
4.如图,将 ABCD的一边BC延长至点E,若∠A=∠D+50°,则∠B等于( )
A.50° B.65° C.70° D.75°
【分析】根据平行四边形的邻角互补求出∠D的度数,再根据平行四边形的对角相等即可得解.
解:∵四边形ABCD是平行四边形,
∴∠A+∠D=180°,∠B=∠D,
∵∠A=∠D+50°,
∴∠D=65°,
∴∠B=65°,
故选:B.
5.下列说法中错误的是( )
A.一组数据的平均数受极端值的影响较大
B.一组数据的平均数、众数、中位数有可能相同
C.如果一组数据的众数是5,那么这组数据中出现次数最多的数据是5
D.一组数据的中位数有时有两个
【分析】根据平均数、众数、中位数的概念逐一分析求解可得.
解:A.一组数据的平均数受极端值的影响较大,此说法正确,此选项不符合题意;
B.在一组数据的平均数、众数、中位数有可能相同,如全部相等的数据,此说法正确,此选项不符合题意;
C.根据众数的定义可知众数是出现次数最多的数,故此选项说法正确,此选项不符合题意;
D.一组数据的中位数是最中间的一个或最中间的两个的平均数,所以不可能有两个,故此选项说法错误,符合题意;
故选:D.
6.下列各式,从左到右变形正确的是( )
A.
B.
C.
D.
【分析】根据分式的基本性质(分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变)判断即可.
解:A、2前面是加号不是乘号,不可以约分,原变形错误,故本选项不符合题意;
B、原式=﹣,原变形错误,故本选项不符合题意;
C、原式==,原变形正确,故本选项符合题意;
D、从左边到右边不正确,原变形错误,故本选项不符合题意;
故选:C.
7.已知3a=3b﹣5,则代数式3a2﹣6ab+3b2﹣3的值为( )
A. B.2 C.22 D.
【分析】已知条件化简为a﹣b=,只需要把所求式子化为用a﹣b表示的式子即可.
解:依题意a﹣b=,
原式=3(a﹣b) ﹣3
=3×(﹣) ﹣3
=
=.
故选:D.
8.如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE⊥DE,则△BDC通过下列变换能与△ACE重合的是( )
A.绕点C逆时针旋转90度
B.沿AB的垂直平分线翻折
C.绕AB的中点M顺时针旋转90度
D.沿DE方向平移
【分析】根据全等三角形的判定定理AAS得到△BDC≌△CEA,则BD=CE,CD=AE.结合平移与旋转的性质进行判断.
解:∵BD⊥DE,AE⊥DE,
∴∠BDC=∠CEA=90°,
又∠ACB=90°,
∴∠BCD=∠CAE(同角的余角相等),
∴在△BDC与△CEA中,
,
∴△BDC≌△CEA(AAS).
∴BD=CE,CD=AE.
A、绕点C旋转后,CB与AC不重合,即△BDC与△ACE不重合,故选项A不符合题意;
B、△BDC与△ACE不关于AB的中垂线对称,则沿AB的中垂线翻折后不重合,故选项B不符合题意;
C、因为△ABC是等腰直角三角形,所以CM⊥AB,所以绕中点M逆时针旋转90度,则△ACE与△BDC重合,故选项C符合题意;
D、先沿ED方向平移△CEA,使点E与点D重合后,再将平移后的三角形绕点D逆时针旋转90度,则△BDC与△ACE重合,故选项D不符合题意;
故选:C.
9.已知一组数据的方差s2=[(3﹣7)2+(8﹣7)2+(11﹣7)2+(a﹣7)2+(b﹣7)2+(c﹣7)2],则a+b+c的值为( )
A.22 B.21 C.20 D.7
【分析】根据方差的定义得出这组数据为3,8,11,a,b,c,其平均数为7,再利用平均数的概念求解可得.
解:由题意知,这组数据为3,8,11,a,b,c,其平均数为7,
则=7,
∴a+b+c=20,
故选:C.
10.如图,在△ABC中,∠BAC=126°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'刚好落在BC边上,且AB'=CB',则∠C'的度数为( )
A.18° B.16° C.15° D.14°
【分析】由旋转的性质可得∠C=∠C',AB=AB',由等腰三角形的性质可得∠C=∠CAB',∠B=∠AB'B,由三角形的外角性质和三角形内角和定理可求解.
解:∵AB'=CB',
∴∠C=∠CAB',
∴∠AB'B=∠C+∠CAB'=2∠C,
∵将△ABC绕点A按逆时针方向旋转得到△AB'C',
∴∠C=∠C',AB=AB',
∴∠B=∠AB'B=2∠C,
∵∠B+∠C+∠CAB=180°,
∴3∠C=180°﹣126°=54°,
∴∠C=18°,
∴∠C'=∠C=18°,
故选:A.
11.如图,点A的坐标为(1,4),点B在x轴上,把△AOB沿x轴向右平移到△CED,若四边形ABDC的面积为8,则点C的坐标为( )
A.( 2,4) B.(3,4) C.(3,3) D.(4,3)
【分析】根据平移的性质得出四边形ABDC是平行四边形,从而得A和C的纵坐标相同,根据四边形ABDC的面积求得AC的长,即可求得C的坐标.
解:∵把△OAB沿x轴向右平移到△ECD,
∴四边形ABDC是平行四边形,
∴AC=BD,A和C的纵坐标相同,
∵四边形ABDC的面积为8,点A的坐标为(1,4),
∴4AC=8,
∴AC=2,
∴C(3,4),
故选:B.
12.如图,在四边形ABCD中,AB∥CD,BC∥AD,且AD=DC,则下列说法:
①四边形ABCD是平行四边形;
②AB=BC;
③AC⊥BD
④AC平分∠BAD;
⑤若AC=6,BD=8,则四边形ABCD的面积为24.
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
【分析】先证四边形ABCD是平行四边形,再证平行四边形ABCD是菱形,即可得出结论.
解:∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,故①正确;
∵AD=DC,
∴平行四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AC平分∠BAD,故②③④正确,
∵AC=6,BD=8,
∴菱形ABCD的面积=AC×BD=×6×8=24,故⑤正确;
正确的个数有5个,
故选:D.
二.填空题。(本大题共6个小题,每小题3分,满分18分)
13.过多边形的一个顶点可做7条对角线,则多边形的内角和为 1440° .
【分析】从多边形一个顶点可作7条对角线,则这个多边形的边数是10,n边形的内角和可以表示成(n﹣2) 180°,代入公式就可以求出内角和.
解:∵过多边形的一个顶点共有7条对角线,
∴n﹣3=7,即n=10,
故该多边形边数为10,
∴(10﹣2) 180°=1440°,
∴这个多边形的内角和为1440°.
故答案为:1440°.
14.如图,将直角△ABC沿斜边AC的方向平移到△DEF的位置,DE交BC于点G,BG=4,EF=10,则线段GC的长 6 .
【分析】根据平移的性质即可得到结论.
解:∵△DEF的是直角三角形ABC沿着斜边AC的方向平移后得到的,BC=EF=10,
∵BG=4,
∴CG=BC﹣BG=EF﹣BG=10﹣4=6,
故答案为:6.
15.若x2﹣5x=﹣5,则x+= 4 .
【分析】先通分得出原式=,变形后把x2﹣5x=﹣5代入,即可求出答案.
解:∵x2﹣5x=﹣5,
∴x+
=
=
=
=
=
=
=4,
故答案为:4.
16.如图,将△ABC绕点A逆时针旋转50°得到△ADE.若∠E=65°,且AD⊥BC于点F,则∠BAC的度数为 75° .
【分析】由旋转的性质可得∠C=∠E=65°,∠BAD=50°,再由垂直的定义可得∠AFC=90°,利用直角三角形两锐角互余可得∠CAF=90°﹣∠C=25°,即可得∠BAC=75°.
解:∵△ABC绕点A逆时针旋转50°得到△ADE,
∴∠C=∠E=65°,∠BAD=50°,
∵AD⊥BC,
∴∠AFC=90°,
∴∠CAF=90°﹣∠C=25°,
∴∠BAC=∠CAF+∠BAD=25°+50°=75°,
故答案为:75°.
17.定义一种法则“*”如下:a*b=,例如:1*2=,若m*3=,则m的值为 2 .
【分析】已知等式利用题中的新定义化简得到分式方程,求出分式方程的解即可得到m的值.
解:根据题中的新定义化简得:
﹣=,
去分母得:3﹣1=m,
解得:m=2,
检验:把m=2代入得:3m≠0,
∴分式方程的解为m=2.
故答案为:2.
18.如图,在平行四边形 ABCD中,AB=3,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 36 .
【分析】根据平行四边形的性质和角平分线的定义可得AE=AB=DE=CD=3,∠BEC=90°,可得BC=AD=3+3=6,再根据勾股定理解答即可.
解:∵BE、CE 分别平分∠ABC 和∠BCD
∴∠EBC=∠ABC,∠ECB=∠BCD,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=2,BC=AD,
∴∠ABC+∠BCD=180°,
∴∠EBC+∠ECB=90°,
∴∠BEC=90°,
∴BE2+CE2=BC2 ,
∵AD∥BC,
∴∠EBC=∠AEB,
∵BE平分∠ABC,
∴∠EBC=∠ABE,
∴∠AEB=∠ABE,
∴AB=AE=3,
同理可证 DE=DC=3,
∴DE+AE=AD=6,
∴BE2+CE2=BC2=AD2=36.
故答案为:36.
三.解答题。(本大题共7个小题,共66分。请在答题卡指定区域内作答.)
19.(1)化简求值:
(﹣)÷,任取一个合适的x的值,求出该代数式的值;
(2)解分式方程:
+3=.
【分析】(1)先将小括号内的式子进行通分计算,然后算括号外面的除法,再根据分式有意义的条件选取合适的x的值,代入求值;
(2)将分式方程转化为整式方程,然后解方程,注意结果要进行检验.
解:(1)原式=[﹣]÷
=
=
=2x+4,
∵x﹣1≠0,x+1≠0,x≠0,
∴x≠±1且x≠0,
∴当x=2时,原式=2×2+4=8;
(2)+3=,
整理,可得:,
去分母,可得:x﹣1+3(x﹣2)=﹣3,
移项,合并同类项,可得:4x=4,
系数化1,得:x=1,
检验,当x=1时,x﹣2≠0,
∴原分式方程的解为x=1.
20.如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,2),B(﹣1,0),C(2,0).
(1)△ABC平移后,其中点C的坐标移到点C1(4,1),请在给定的坐标系中画出△A1B1C1.
(2)把△A1B1C1绕着点A1逆时针方向旋转90°,画出旋转后的△A1B2C2.
【分析】(1)利用平移变换的性质分别作出A,B,C 的对应点A1,B1,C1即可;
(2)利用旋转变换的性质分别作出B1,C1的对应点B2,C2即可.
解:(1)如图△A1B1C1就是所要求做的三角形;
(2)如图,△A1B2C2就是所要求做的三角形.
21.学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明 13.3 0.004
李亮 13.3 0.02
(1)张明第3次的成绩为 13.3 秒,李亮第2次的成绩为 13.4 秒.
(2)张明成绩的平均数为 13.3 秒;李亮成绩的中位数为 13.3 秒.
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
【分析】(1)利用折线统计图即可求解;
(2)利用平均数和中位数的定义求解;
(3)根据平均数、中位数以及方差的意义进行判断.
解:(1)张明第3次的成绩为13.3秒,李亮第2次的成绩为13.4秒.
故答案为13.3,13.4;
(2)张明成绩的平均数为=13.3(秒);
将李亮的5次成绩按从小到大的顺序排列为:13.1,13.2,13.3,13.4,13.5,
其中第三个数是13.3,所以中位数为13.3秒;
故答案为13.3,13.3;
(3)选择张明.
理由如下:因为两人平均数和中位数相同,但张明成绩的方差小于李亮成绩的方差,所以张明成绩比李亮成绩稳定,因此选择张明.
22.如图,平行四边形ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F,连接AF.
(1)求证:BE=DF;
(2)若EF⊥AC,△ADF的周长是13,则平行四边形ABCD的周长为 26 .
【分析】(1)证明出△OBE≌△ODF,即有BE=DF;
(2)由EF垂直平分AC得△ADF的周长为AD+DC=13,进而平行四边形ABCD的周长为13×2=26.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OB=OD,
∴∠ABD=∠CDB,
在△OBE和△ODF中,
,
∴△OBE≌△ODF(ASA),
∴BE=DF;
(2)∵EF⊥AC,AO=OC,
∴AF=CF,
∴△ADF的周长为AD+DF+FA=AD+DF+CF=AD+DC=13,
∴平行四边形ABCD的周长为13×2=26.
故答案为:26.
23.随着智能分拣设备在快递业务中的普及,快件分拣效率大幅提高.使用某品牌智能分拣设备,每人每小时分拣的快件量是传统分拣方式的25倍,经过测试,由5人用此设备分拣6000件快件的时间,比20人用传统方式分拣同样数量的快件节省3小时.
(1)使用智能分拣设备后,每人每小时可分拣快件多少件?
(2)已知某快递中转站平均每天需要分拣10万件快件,每天工作时间为8小时,如果使用此智能分拣设备,每天只需要安排多少名工人就可以完成分拣工作?
【分析】(1)设使用传统分拣方式,每人每小时可分拣快件x件,则使用智能分拣设备后,每人每小时可分拣快件25x件,利用工作时间=工作总量÷工作效率,结合5人用此设备分拣6000件快件的时间比20人用传统方式分拣同样数量的快件节省3小时,列出分式方程,解方程即可;
(2)利用需要的工人人数=每天需要分拣快件的总数÷每天的工作时间÷每人每小时可分拣快件的数量,即可求出结论.
解:(1)设使用传统分拣方式,每人每小时可分拣快件x件,则使用智能分拣设备后,每人每小时可分拣快件25x件,
依题意得:﹣=3,
解得:x=84,
经检验,x=84是原方程的解,且符合题意,
则25x=2100.
答:使用智能分拣设备后,每人每小时可分拣快件2100件.
(2)100000÷8÷2100=5(人),5+1=6(人).
答:每天只需要安排6名工人就可以完成分拣工作.
24.请阅读下列材料:
我们可以通过以下方法求代数式x2+6x+5的最小值.
x2+6x+5=x2+2 x 3+32﹣32+5=(x+3)2﹣4;
∵(x+3)2≥0;
∴当x=﹣3时,代数式x2+6x+5的最小值为﹣4.
请根据上述的方法,解答下列问题:
(1)x2+6x﹣1=(x+m)2+n,则mn的值为 ﹣30 .
(2)求代数式的最大值.
(3)若代数式2x2+kx+6的最小值为2,求k的值.
【分析】(1)根据配方的过程求得m、n的值代入求值即可.
(2)先利用完全平方公式配方,再根据偶次方非负数的性质列式求解.
(3)先利用完全平方公式配方,再根据偶次方非负数的性质列式求.
解:(1)x +6x﹣1=x+2 x 3+3 ﹣3 ﹣1=(x+3)2﹣10=(x+m) +n.
∴mn=3x(﹣10)=﹣30.
故答案为:﹣30.
(2)=5==.
∵∴,
∴代数式的最大值为11.
(3)2x2+kx+6=2(x)+6
=2+6
=2+6.
∵∴代数式2x2+kx+6有最小值为,
∵代数式2x2+kx+6的最小值为2,
∴解之:k=.
25.已知,△ABC、△ADE是等腰三角形,AB=AC,AD=AE,D是BC上一点,∠DAE=∠BAC,过点E作BC的平行线交AB于点F,连接CF.
(1)如图1,求证:四边形CDEF是平行四边形;
(2)如图2,连接BE、DF,若AD⊥BC,在不添加任何辅助线的情况下,请直接写出图2中长度等于BC的长的的线段.
【分析】(1)由SAS证明△ACD≌△ABE得出CD=BE,∠ACD=∠ABE,由平行线的性质得出∠ABC=∠EFB,得出∠ABE=∠EFB,证出EB=EF,得出EF=CD,即可得出结论,
(2)证明四边形BEFD是平行四边形可得BE=DF,结合(1)即可得结论.
【解答】(1)如答图1,证明:连接BE,
∵∠BAC=∠DAE,
∴∠DAC=∠EAB,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴CD=BE,∠ACD=∠ABE,
∵EF∥BC,
∴∠ABC=∠EFB,
∴∠ABE=∠EFB,
∴EB=EF,
∴EF=CD,
∵EF∥BC,
∴四边形EDCF是平行四边形;
(2)∵AB=AC,AD⊥BC,
∴BD=CD=BC,
由(1)知CD=BE=EF,
∴BD=EF,
∵E作BC的平行线交AB于点F,即BD||EF,
∴四边形BEFD是平行四边形,
∴BE=DF,
∴BD=CD=BE=EF=DF=BC,
故答案为:BD,CD,BE,EF,DF.
一.选择题。(本大题共12个小题,每小题3分,满分36分)
1.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.一棋谱中四部分的截图由黑白棋子摆成的图案是中心对称的是( )
A. B. C. D.
2.已知四边形ABCD的对角线AC,BD相交于点O,OB=OD.则下列条件中不能判定四边形ABCD为平行四边形的是( )
A.OA=OC B.AB∥CD C.AD∥BC D.AB=CD
3.若式子+有意义,则x满足的条件是( )
A.x≠3且x≠﹣3 B.x≠3且x≠4 C.x≠4且x≠﹣5 D.x≠﹣3且x≠﹣5
4.如图,将 ABCD的一边BC延长至点E,若∠A=∠D+50°,则∠B等于( )
A.50° B.65° C.70° D.75°
5.下列说法中错误的是( )
A.一组数据的平均数受极端值的影响较大
B.一组数据的平均数、众数、中位数有可能相同
C.如果一组数据的众数是5,那么这组数据中出现次数最多的数据是5
D.一组数据的中位数有时有两个
6.下列各式,从左到右变形正确的是( )
A.
B.
C.
D.
7.已知3a=3b﹣5,则代数式3a2﹣6ab+3b2﹣3的值为( )
A. B.2 C.22 D.
8.如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE⊥DE,则△BDC通过下列变换能与△ACE重合的是( )
A.绕点C逆时针旋转90度
B.沿AB的垂直平分线翻折
C.绕AB的中点M顺时针旋转90度
D.沿DE方向平移
9.已知一组数据的方差s2=[(3﹣7)2+(8﹣7)2+(11﹣7)2+(a﹣7)2+(b﹣7)2+(c﹣7)2],则a+b+c的值为( )
A.22 B.21 C.20 D.7
10.如图,在△ABC中,∠BAC=126°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'刚好落在BC边上,且AB'=CB',则∠C'的度数为( )
A.18° B.16° C.15° D.14°
11.如图,点A的坐标为(1,4),点B在x轴上,把△AOB沿x轴向右平移到△CED,若四边形ABDC的面积为8,则点C的坐标为( )
A.( 2,4) B.(3,4) C.(3,3) D.(4,3)
12.如图,在四边形ABCD中,AB∥CD,BC∥AD,且AD=DC,则下列说法:
①四边形ABCD是平行四边形;
②AB=BC;
③AC⊥BD
④AC平分∠BAD;
⑤若AC=6,BD=8,则四边形ABCD的面积为24.
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
二.填空题。(本大题共6个小题,每小题3分,满分18分)
13.过多边形的一个顶点可做7条对角线,则多边形的内角和为 .
14.如图,将直角△ABC沿斜边AC的方向平移到△DEF的位置,DE交BC于点G,BG=4,EF=10,则线段GC的长 .
15.若x2﹣5x=﹣5,则x+= .
16.如图,将△ABC绕点A逆时针旋转50°得到△ADE.若∠E=65°,且AD⊥BC于点F,则∠BAC的度数为 .
17.定义一种法则“*”如下:a*b=,例如:1*2=,若m*3=,则m的值为 .
18.如图,在平行四边形 ABCD中,AB=3,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 .
三.解答题。(本大题共7个小题,共66分。请在答题卡指定区域内作答.)
19.(1)化简求值:
(﹣)÷,任取一个合适的x的值,求出该代数式的值;
(2)解分式方程:
+3=.
20.如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,2),B(﹣1,0),C(2,0).
(1)△ABC平移后,其中点C的坐标移到点C1(4,1),请在给定的坐标系中画出△A1B1C1.
(2)把△A1B1C1绕着点A1逆时针方向旋转90°,画出旋转后的△A1B2C2.
21.学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明 13.3 0.004
李亮 13.3 0.02
(1)张明第3次的成绩为 秒,李亮第2次的成绩为 秒.
(2)张明成绩的平均数为 秒;李亮成绩的中位数为 秒.
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
22.如图,平行四边形ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F,连接AF.
(1)求证:BE=DF;
(2)若EF⊥AC,△ADF的周长是13,则平行四边形ABCD的周长为 .
23.随着智能分拣设备在快递业务中的普及,快件分拣效率大幅提高.使用某品牌智能分拣设备,每人每小时分拣的快件量是传统分拣方式的25倍,经过测试,由5人用此设备分拣6000件快件的时间,比20人用传统方式分拣同样数量的快件节省3小时.
(1)使用智能分拣设备后,每人每小时可分拣快件多少件?
(2)已知某快递中转站平均每天需要分拣10万件快件,每天工作时间为8小时,如果使用此智能分拣设备,每天只需要安排多少名工人就可以完成分拣工作?
24.请阅读下列材料:
我们可以通过以下方法求代数式x2+6x+5的最小值.
x2+6x+5=x2+2 x 3+32﹣32+5=(x+3)2﹣4;
∵(x+3)2≥0;
∴当x=﹣3时,代数式x2+6x+5的最小值为﹣4.
请根据上述的方法,解答下列问题:
(1)x2+6x﹣1=(x+m)2+n,则mn的值为 .
(2)求代数式的最大值.
(3)若代数式2x2+kx+6的最小值为2,求k的值.
25.已知,△ABC、△ADE是等腰三角形,AB=AC,AD=AE,D是BC上一点,∠DAE=∠BAC,过点E作BC的平行线交AB于点F,连接CF.
(1)如图1,求证:四边形CDEF是平行四边形;
(2)如图2,连接BE、DF,若AD⊥BC,在不添加任何辅助线的情况下,请直接写出图2中长度等于BC的长的的线段.
参考答案
一.选择题。(本大题共12个小题,每小题3分,满分36分)
1.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.一棋谱中四部分的截图由黑白棋子摆成的图案是中心对称的是( )
A. B. C. D.
【分析】把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,根据中心对称图形的概念求解.
解:选项A能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形;
选项B、C、D不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形;
故选:A.
2.已知四边形ABCD的对角线AC,BD相交于点O,OB=OD.则下列条件中不能判定四边形ABCD为平行四边形的是( )
A.OA=OC B.AB∥CD C.AD∥BC D.AB=CD
【分析】根据平行四边形的判定定理分别进行分析即可.
解:A、∵OA=OC,OB=OD,∴四边形ABCD是平行四边形,不符合题意;
B、∵AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠ODC,
∵OB=OD,
∴△ABO≌△DCO(AAS),
∴AB=CD,
∴四边形ABCD是平行四边形,不符合题意;
C、∵AD∥BC,
∴∠OBC=∠ODA,∠OCB=∠OAD,
∵OB=OD,
∴△OBC≌△ODC(AAS),
∴AD=BC,
∴四边形ABCD是平行四边形,不符合题意;
D、∵AB=CD,OB=OD,不能判断四边形ABCD是平行四边形,符合题意;
故选:D.
3.若式子+有意义,则x满足的条件是( )
A.x≠3且x≠﹣3 B.x≠3且x≠4 C.x≠4且x≠﹣5 D.x≠﹣3且x≠﹣5
【分析】直接利用分式有意义的条件得出答案.
解:∵分式有意义,
∴x﹣3≠0,x﹣4≠0,
∴x≠3且x≠4,
故选:B.
4.如图,将 ABCD的一边BC延长至点E,若∠A=∠D+50°,则∠B等于( )
A.50° B.65° C.70° D.75°
【分析】根据平行四边形的邻角互补求出∠D的度数,再根据平行四边形的对角相等即可得解.
解:∵四边形ABCD是平行四边形,
∴∠A+∠D=180°,∠B=∠D,
∵∠A=∠D+50°,
∴∠D=65°,
∴∠B=65°,
故选:B.
5.下列说法中错误的是( )
A.一组数据的平均数受极端值的影响较大
B.一组数据的平均数、众数、中位数有可能相同
C.如果一组数据的众数是5,那么这组数据中出现次数最多的数据是5
D.一组数据的中位数有时有两个
【分析】根据平均数、众数、中位数的概念逐一分析求解可得.
解:A.一组数据的平均数受极端值的影响较大,此说法正确,此选项不符合题意;
B.在一组数据的平均数、众数、中位数有可能相同,如全部相等的数据,此说法正确,此选项不符合题意;
C.根据众数的定义可知众数是出现次数最多的数,故此选项说法正确,此选项不符合题意;
D.一组数据的中位数是最中间的一个或最中间的两个的平均数,所以不可能有两个,故此选项说法错误,符合题意;
故选:D.
6.下列各式,从左到右变形正确的是( )
A.
B.
C.
D.
【分析】根据分式的基本性质(分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变)判断即可.
解:A、2前面是加号不是乘号,不可以约分,原变形错误,故本选项不符合题意;
B、原式=﹣,原变形错误,故本选项不符合题意;
C、原式==,原变形正确,故本选项符合题意;
D、从左边到右边不正确,原变形错误,故本选项不符合题意;
故选:C.
7.已知3a=3b﹣5,则代数式3a2﹣6ab+3b2﹣3的值为( )
A. B.2 C.22 D.
【分析】已知条件化简为a﹣b=,只需要把所求式子化为用a﹣b表示的式子即可.
解:依题意a﹣b=,
原式=3(a﹣b) ﹣3
=3×(﹣) ﹣3
=
=.
故选:D.
8.如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE⊥DE,则△BDC通过下列变换能与△ACE重合的是( )
A.绕点C逆时针旋转90度
B.沿AB的垂直平分线翻折
C.绕AB的中点M顺时针旋转90度
D.沿DE方向平移
【分析】根据全等三角形的判定定理AAS得到△BDC≌△CEA,则BD=CE,CD=AE.结合平移与旋转的性质进行判断.
解:∵BD⊥DE,AE⊥DE,
∴∠BDC=∠CEA=90°,
又∠ACB=90°,
∴∠BCD=∠CAE(同角的余角相等),
∴在△BDC与△CEA中,
,
∴△BDC≌△CEA(AAS).
∴BD=CE,CD=AE.
A、绕点C旋转后,CB与AC不重合,即△BDC与△ACE不重合,故选项A不符合题意;
B、△BDC与△ACE不关于AB的中垂线对称,则沿AB的中垂线翻折后不重合,故选项B不符合题意;
C、因为△ABC是等腰直角三角形,所以CM⊥AB,所以绕中点M逆时针旋转90度,则△ACE与△BDC重合,故选项C符合题意;
D、先沿ED方向平移△CEA,使点E与点D重合后,再将平移后的三角形绕点D逆时针旋转90度,则△BDC与△ACE重合,故选项D不符合题意;
故选:C.
9.已知一组数据的方差s2=[(3﹣7)2+(8﹣7)2+(11﹣7)2+(a﹣7)2+(b﹣7)2+(c﹣7)2],则a+b+c的值为( )
A.22 B.21 C.20 D.7
【分析】根据方差的定义得出这组数据为3,8,11,a,b,c,其平均数为7,再利用平均数的概念求解可得.
解:由题意知,这组数据为3,8,11,a,b,c,其平均数为7,
则=7,
∴a+b+c=20,
故选:C.
10.如图,在△ABC中,∠BAC=126°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'刚好落在BC边上,且AB'=CB',则∠C'的度数为( )
A.18° B.16° C.15° D.14°
【分析】由旋转的性质可得∠C=∠C',AB=AB',由等腰三角形的性质可得∠C=∠CAB',∠B=∠AB'B,由三角形的外角性质和三角形内角和定理可求解.
解:∵AB'=CB',
∴∠C=∠CAB',
∴∠AB'B=∠C+∠CAB'=2∠C,
∵将△ABC绕点A按逆时针方向旋转得到△AB'C',
∴∠C=∠C',AB=AB',
∴∠B=∠AB'B=2∠C,
∵∠B+∠C+∠CAB=180°,
∴3∠C=180°﹣126°=54°,
∴∠C=18°,
∴∠C'=∠C=18°,
故选:A.
11.如图,点A的坐标为(1,4),点B在x轴上,把△AOB沿x轴向右平移到△CED,若四边形ABDC的面积为8,则点C的坐标为( )
A.( 2,4) B.(3,4) C.(3,3) D.(4,3)
【分析】根据平移的性质得出四边形ABDC是平行四边形,从而得A和C的纵坐标相同,根据四边形ABDC的面积求得AC的长,即可求得C的坐标.
解:∵把△OAB沿x轴向右平移到△ECD,
∴四边形ABDC是平行四边形,
∴AC=BD,A和C的纵坐标相同,
∵四边形ABDC的面积为8,点A的坐标为(1,4),
∴4AC=8,
∴AC=2,
∴C(3,4),
故选:B.
12.如图,在四边形ABCD中,AB∥CD,BC∥AD,且AD=DC,则下列说法:
①四边形ABCD是平行四边形;
②AB=BC;
③AC⊥BD
④AC平分∠BAD;
⑤若AC=6,BD=8,则四边形ABCD的面积为24.
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
【分析】先证四边形ABCD是平行四边形,再证平行四边形ABCD是菱形,即可得出结论.
解:∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,故①正确;
∵AD=DC,
∴平行四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AC平分∠BAD,故②③④正确,
∵AC=6,BD=8,
∴菱形ABCD的面积=AC×BD=×6×8=24,故⑤正确;
正确的个数有5个,
故选:D.
二.填空题。(本大题共6个小题,每小题3分,满分18分)
13.过多边形的一个顶点可做7条对角线,则多边形的内角和为 1440° .
【分析】从多边形一个顶点可作7条对角线,则这个多边形的边数是10,n边形的内角和可以表示成(n﹣2) 180°,代入公式就可以求出内角和.
解:∵过多边形的一个顶点共有7条对角线,
∴n﹣3=7,即n=10,
故该多边形边数为10,
∴(10﹣2) 180°=1440°,
∴这个多边形的内角和为1440°.
故答案为:1440°.
14.如图,将直角△ABC沿斜边AC的方向平移到△DEF的位置,DE交BC于点G,BG=4,EF=10,则线段GC的长 6 .
【分析】根据平移的性质即可得到结论.
解:∵△DEF的是直角三角形ABC沿着斜边AC的方向平移后得到的,BC=EF=10,
∵BG=4,
∴CG=BC﹣BG=EF﹣BG=10﹣4=6,
故答案为:6.
15.若x2﹣5x=﹣5,则x+= 4 .
【分析】先通分得出原式=,变形后把x2﹣5x=﹣5代入,即可求出答案.
解:∵x2﹣5x=﹣5,
∴x+
=
=
=
=
=
=
=4,
故答案为:4.
16.如图,将△ABC绕点A逆时针旋转50°得到△ADE.若∠E=65°,且AD⊥BC于点F,则∠BAC的度数为 75° .
【分析】由旋转的性质可得∠C=∠E=65°,∠BAD=50°,再由垂直的定义可得∠AFC=90°,利用直角三角形两锐角互余可得∠CAF=90°﹣∠C=25°,即可得∠BAC=75°.
解:∵△ABC绕点A逆时针旋转50°得到△ADE,
∴∠C=∠E=65°,∠BAD=50°,
∵AD⊥BC,
∴∠AFC=90°,
∴∠CAF=90°﹣∠C=25°,
∴∠BAC=∠CAF+∠BAD=25°+50°=75°,
故答案为:75°.
17.定义一种法则“*”如下:a*b=,例如:1*2=,若m*3=,则m的值为 2 .
【分析】已知等式利用题中的新定义化简得到分式方程,求出分式方程的解即可得到m的值.
解:根据题中的新定义化简得:
﹣=,
去分母得:3﹣1=m,
解得:m=2,
检验:把m=2代入得:3m≠0,
∴分式方程的解为m=2.
故答案为:2.
18.如图,在平行四边形 ABCD中,AB=3,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 36 .
【分析】根据平行四边形的性质和角平分线的定义可得AE=AB=DE=CD=3,∠BEC=90°,可得BC=AD=3+3=6,再根据勾股定理解答即可.
解:∵BE、CE 分别平分∠ABC 和∠BCD
∴∠EBC=∠ABC,∠ECB=∠BCD,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=2,BC=AD,
∴∠ABC+∠BCD=180°,
∴∠EBC+∠ECB=90°,
∴∠BEC=90°,
∴BE2+CE2=BC2 ,
∵AD∥BC,
∴∠EBC=∠AEB,
∵BE平分∠ABC,
∴∠EBC=∠ABE,
∴∠AEB=∠ABE,
∴AB=AE=3,
同理可证 DE=DC=3,
∴DE+AE=AD=6,
∴BE2+CE2=BC2=AD2=36.
故答案为:36.
三.解答题。(本大题共7个小题,共66分。请在答题卡指定区域内作答.)
19.(1)化简求值:
(﹣)÷,任取一个合适的x的值,求出该代数式的值;
(2)解分式方程:
+3=.
【分析】(1)先将小括号内的式子进行通分计算,然后算括号外面的除法,再根据分式有意义的条件选取合适的x的值,代入求值;
(2)将分式方程转化为整式方程,然后解方程,注意结果要进行检验.
解:(1)原式=[﹣]÷
=
=
=2x+4,
∵x﹣1≠0,x+1≠0,x≠0,
∴x≠±1且x≠0,
∴当x=2时,原式=2×2+4=8;
(2)+3=,
整理,可得:,
去分母,可得:x﹣1+3(x﹣2)=﹣3,
移项,合并同类项,可得:4x=4,
系数化1,得:x=1,
检验,当x=1时,x﹣2≠0,
∴原分式方程的解为x=1.
20.如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,2),B(﹣1,0),C(2,0).
(1)△ABC平移后,其中点C的坐标移到点C1(4,1),请在给定的坐标系中画出△A1B1C1.
(2)把△A1B1C1绕着点A1逆时针方向旋转90°,画出旋转后的△A1B2C2.
【分析】(1)利用平移变换的性质分别作出A,B,C 的对应点A1,B1,C1即可;
(2)利用旋转变换的性质分别作出B1,C1的对应点B2,C2即可.
解:(1)如图△A1B1C1就是所要求做的三角形;
(2)如图,△A1B2C2就是所要求做的三角形.
21.学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明 13.3 0.004
李亮 13.3 0.02
(1)张明第3次的成绩为 13.3 秒,李亮第2次的成绩为 13.4 秒.
(2)张明成绩的平均数为 13.3 秒;李亮成绩的中位数为 13.3 秒.
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
【分析】(1)利用折线统计图即可求解;
(2)利用平均数和中位数的定义求解;
(3)根据平均数、中位数以及方差的意义进行判断.
解:(1)张明第3次的成绩为13.3秒,李亮第2次的成绩为13.4秒.
故答案为13.3,13.4;
(2)张明成绩的平均数为=13.3(秒);
将李亮的5次成绩按从小到大的顺序排列为:13.1,13.2,13.3,13.4,13.5,
其中第三个数是13.3,所以中位数为13.3秒;
故答案为13.3,13.3;
(3)选择张明.
理由如下:因为两人平均数和中位数相同,但张明成绩的方差小于李亮成绩的方差,所以张明成绩比李亮成绩稳定,因此选择张明.
22.如图,平行四边形ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F,连接AF.
(1)求证:BE=DF;
(2)若EF⊥AC,△ADF的周长是13,则平行四边形ABCD的周长为 26 .
【分析】(1)证明出△OBE≌△ODF,即有BE=DF;
(2)由EF垂直平分AC得△ADF的周长为AD+DC=13,进而平行四边形ABCD的周长为13×2=26.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OB=OD,
∴∠ABD=∠CDB,
在△OBE和△ODF中,
,
∴△OBE≌△ODF(ASA),
∴BE=DF;
(2)∵EF⊥AC,AO=OC,
∴AF=CF,
∴△ADF的周长为AD+DF+FA=AD+DF+CF=AD+DC=13,
∴平行四边形ABCD的周长为13×2=26.
故答案为:26.
23.随着智能分拣设备在快递业务中的普及,快件分拣效率大幅提高.使用某品牌智能分拣设备,每人每小时分拣的快件量是传统分拣方式的25倍,经过测试,由5人用此设备分拣6000件快件的时间,比20人用传统方式分拣同样数量的快件节省3小时.
(1)使用智能分拣设备后,每人每小时可分拣快件多少件?
(2)已知某快递中转站平均每天需要分拣10万件快件,每天工作时间为8小时,如果使用此智能分拣设备,每天只需要安排多少名工人就可以完成分拣工作?
【分析】(1)设使用传统分拣方式,每人每小时可分拣快件x件,则使用智能分拣设备后,每人每小时可分拣快件25x件,利用工作时间=工作总量÷工作效率,结合5人用此设备分拣6000件快件的时间比20人用传统方式分拣同样数量的快件节省3小时,列出分式方程,解方程即可;
(2)利用需要的工人人数=每天需要分拣快件的总数÷每天的工作时间÷每人每小时可分拣快件的数量,即可求出结论.
解:(1)设使用传统分拣方式,每人每小时可分拣快件x件,则使用智能分拣设备后,每人每小时可分拣快件25x件,
依题意得:﹣=3,
解得:x=84,
经检验,x=84是原方程的解,且符合题意,
则25x=2100.
答:使用智能分拣设备后,每人每小时可分拣快件2100件.
(2)100000÷8÷2100=5(人),5+1=6(人).
答:每天只需要安排6名工人就可以完成分拣工作.
24.请阅读下列材料:
我们可以通过以下方法求代数式x2+6x+5的最小值.
x2+6x+5=x2+2 x 3+32﹣32+5=(x+3)2﹣4;
∵(x+3)2≥0;
∴当x=﹣3时,代数式x2+6x+5的最小值为﹣4.
请根据上述的方法,解答下列问题:
(1)x2+6x﹣1=(x+m)2+n,则mn的值为 ﹣30 .
(2)求代数式的最大值.
(3)若代数式2x2+kx+6的最小值为2,求k的值.
【分析】(1)根据配方的过程求得m、n的值代入求值即可.
(2)先利用完全平方公式配方,再根据偶次方非负数的性质列式求解.
(3)先利用完全平方公式配方,再根据偶次方非负数的性质列式求.
解:(1)x +6x﹣1=x+2 x 3+3 ﹣3 ﹣1=(x+3)2﹣10=(x+m) +n.
∴mn=3x(﹣10)=﹣30.
故答案为:﹣30.
(2)=5==.
∵∴,
∴代数式的最大值为11.
(3)2x2+kx+6=2(x)+6
=2+6
=2+6.
∵∴代数式2x2+kx+6有最小值为,
∵代数式2x2+kx+6的最小值为2,
∴解之:k=.
25.已知,△ABC、△ADE是等腰三角形,AB=AC,AD=AE,D是BC上一点,∠DAE=∠BAC,过点E作BC的平行线交AB于点F,连接CF.
(1)如图1,求证:四边形CDEF是平行四边形;
(2)如图2,连接BE、DF,若AD⊥BC,在不添加任何辅助线的情况下,请直接写出图2中长度等于BC的长的的线段.
【分析】(1)由SAS证明△ACD≌△ABE得出CD=BE,∠ACD=∠ABE,由平行线的性质得出∠ABC=∠EFB,得出∠ABE=∠EFB,证出EB=EF,得出EF=CD,即可得出结论,
(2)证明四边形BEFD是平行四边形可得BE=DF,结合(1)即可得结论.
【解答】(1)如答图1,证明:连接BE,
∵∠BAC=∠DAE,
∴∠DAC=∠EAB,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴CD=BE,∠ACD=∠ABE,
∵EF∥BC,
∴∠ABC=∠EFB,
∴∠ABE=∠EFB,
∴EB=EF,
∴EF=CD,
∵EF∥BC,
∴四边形EDCF是平行四边形;
(2)∵AB=AC,AD⊥BC,
∴BD=CD=BC,
由(1)知CD=BE=EF,
∴BD=EF,
∵E作BC的平行线交AB于点F,即BD||EF,
∴四边形BEFD是平行四边形,
∴BE=DF,
∴BD=CD=BE=EF=DF=BC,
故答案为:BD,CD,BE,EF,DF.
同课章节目录
