2021-2022学年河北省张家口市桥东区九年级(下)开学数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年河北省张家口市桥东区九年级(下)开学数学试卷(Word版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 812.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 00:00:00 | ||
图片预览



文档简介
2021-2022学年河北省张家口市桥东区九年级(下)开学数学试卷
一、选择题(每小题3分)
1.下列各数中,最小的数是( )
A.0 B.1 C.﹣1 D.﹣
2.计算:﹣a2+2a2=( )
A.a2 B.﹣a2 C.2a2 D.0
3.如图是五个相同的小正方体搭成的几何体,其俯视图是( )
A. B.
C. D.
4.PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,是衡量空气污染程度的重要指标.将0.0000025用科学记数法表示为2.5×10n,则n的值是( )
A.﹣5 B.﹣6 C.﹣7 D.﹣8
5.如图,∠1=30°,∠B=60°,AB⊥AC,则下列说法正确的是( )
A.AB∥CD B.AD∥BC
C.AC⊥CD D.∠DAB+∠D=180°
6.已知(x﹣1)3=ax3+bx2+cx+d,则a+b+c+d的值为( )
A.﹣1 B.0 C.1 D.不能确定
7.如图,在直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是﹣1,则菱形OACB的边长为( )
A.3 B. C.5 D.
8.如果关于x的一元二次方程x2+2x﹣m=0有实数根,则m的取值范围是( )
A.m≥﹣1 B.m≤﹣1 C.m>1 D.m<1
9.如图,EF是△ABC纸片的中位线,将△AEF沿EF所在的直线折叠,点A落在BC边上的点D处,已知△AEF的面积为7,则图中阴影部分的面积为( )
A.7 B.14 C.21 D.28
10.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
A.88° B.92° C.106° D.136°
11.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于( )
A.3 B. C.2 D.
12.已知x2﹣4x﹣1=0,则代数式﹣的值是( )
A.7 B.6 C.5 D.﹣5
13.如图是反比例函数y=和y=﹣在x轴上方的图象,x轴的平行线AB分别与这两个函数图象相交于点A,B,点P在x轴上.则点P从左到右的运动过程中,△APB的面积是( )
A.10 B.4
C.5 D.从小变大再变小
二、填空题(每小题3分)
14.分解因式:ax2﹣4a= .
15.不等式﹣3<0的最大整数解是 .
16.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为 km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为 km.
三、解答题(共52分)
17.某书店新进了一批图书,甲、乙两种书的进价分别为4元/本、10元/本.现购进m本甲种书和n本乙种书,共付款Q元.
(1)用含m,n的代数式表示Q;
(2)若共购进5×104本甲种书及3×103本乙种书,用科学记数法表示Q的值.
18.已知训练场球筐中有A、B两种品牌的乒乓球共101个,设A品牌乒乓球有x个.
(1)淇淇说:“筐里B品牌球是A品牌球的两倍.”嘉嘉根据她的说法列出了方程:101﹣x=2x.请用嘉嘉所列方程分析淇淇的说法是否正确;
(2)据工作人员透露:B品牌球比A品牌球至少多28个,试通过列不等式的方法说明A品牌球最多有几个.
19.不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,现从中任意摸出一个是红球的概率为.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率.
20.小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,如图所示,图中的线段y1、y2分别表示小东、小明离B地的距离y1、y2(千米)与所用时间x(小时)的关系.
(1)写出y1、y2与x的关系式: , ;
(2)试用文字说明:交点P所表示的实际意义.
(3)试求出A、B两地之间的距离.
(4)求出小东、小明相距4千米时出发的时间.
21.如图,在△ABC中,∠BAC=90°,∠B=60°,AB=2.AD⊥BC于D.E为边BC上的一个(不与B、C重合)点,且AE⊥EF于E,∠EAF=∠B,EF、AF相交于点F.
(1)填空:AC= ;∠F= .
(2)当BD=DE时,证明:△ABC≌△EAF.
(3)△EAF面积的最小值是 .
(4)当△EAF的内心在△ABC的外部时,直接写出AE的范围 .
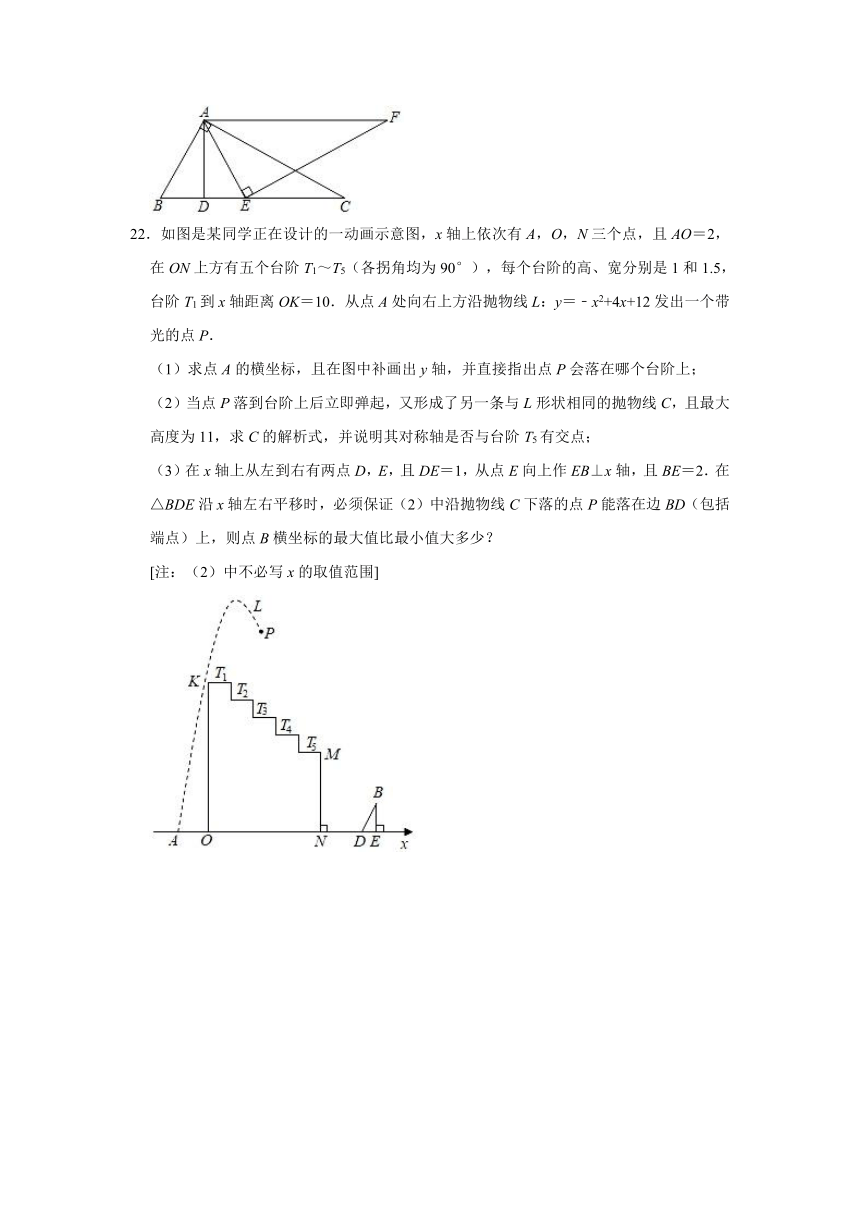
22.如图是某同学正在设计的一动画示意图,x轴上依次有A,O,N三个点,且AO=2,在ON上方有五个台阶T1~T5(各拐角均为90°),每个台阶的高、宽分别是1和1.5,台阶T1到x轴距离OK=10.从点A处向右上方沿抛物线L:y=﹣x2+4x+12发出一个带光的点P.
(1)求点A的横坐标,且在图中补画出y轴,并直接指出点P会落在哪个台阶上;
(2)当点P落到台阶上后立即弹起,又形成了另一条与L形状相同的抛物线C,且最大高度为11,求C的解析式,并说明其对称轴是否与台阶T5有交点;
(3)在x轴上从左到右有两点D,E,且DE=1,从点E向上作EB⊥x轴,且BE=2.在△BDE沿x轴左右平移时,必须保证(2)中沿抛物线C下落的点P能落在边BD(包括端点)上,则点B横坐标的最大值比最小值大多少?
[注:(2)中不必写x的取值范围]
参考答案
一、选择题(每小题3分)
1.下列各数中,最小的数是( )
A.0 B.1 C.﹣1 D.﹣
【分析】根据正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,进行比较.
解:∵正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,
∴﹣<﹣1<0<1,
故选:D.
2.计算:﹣a2+2a2=( )
A.a2 B.﹣a2 C.2a2 D.0
【分析】根据合并同类项法则,合并同类项时,系数相加减,字母及其指数不变,据此计算即可得出正确选项.
解:﹣a2+2a2=(﹣1+2)a2=a2,
故选:A.
3.如图是五个相同的小正方体搭成的几何体,其俯视图是( )
A. B.
C. D.
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
解:如图是五个相同的小正方体搭成的几何体,其俯视图是.
故选:C.
4.PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,是衡量空气污染程度的重要指标.将0.0000025用科学记数法表示为2.5×10n,则n的值是( )
A.﹣5 B.﹣6 C.﹣7 D.﹣8
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.0000025=2.5×10﹣6,
∴n=﹣6.
故选:B.
5.如图,∠1=30°,∠B=60°,AB⊥AC,则下列说法正确的是( )
A.AB∥CD B.AD∥BC
C.AC⊥CD D.∠DAB+∠D=180°
【分析】因为AB⊥AC,所以∠BAC=90°,又因为∠1=30°,∠B=60°,则可求得∠1=∠BCA=30°,故AD∥BC.
解:∵AB⊥AC,
∴∠BAC=90°.
∵∠1=30°,∠B=60°,
∴∠BCA=30°.
∴∠1=∠BCA.
∴AD∥BC.
故选:B.
6.已知(x﹣1)3=ax3+bx2+cx+d,则a+b+c+d的值为( )
A.﹣1 B.0 C.1 D.不能确定
【分析】令x=1,即可求出原式的值.
解:把x=1代入(x﹣1)3=ax3+bx2+cx+d,
得a+b+c+d=0.
故选:B.
7.如图,在直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是﹣1,则菱形OACB的边长为( )
A.3 B. C.5 D.
【分析】首先连接AB交OC于点D,由菱形OACB中,点C的坐标是(4,0),点B的纵坐标是﹣1,即可求得菱形OACB的边长.
解:连接AB交OC于点D,
∵四边形ABCD是菱形,
∴AB⊥OC,OD=CD,AD=BD,
∵点C的坐标是(4,0),点B的纵坐标是﹣1,
∴OC=4,BD=AD=1,
∴OD=CD=2,
∴菱形OACB的边长为=.
故选:D.
8.如果关于x的一元二次方程x2+2x﹣m=0有实数根,则m的取值范围是( )
A.m≥﹣1 B.m≤﹣1 C.m>1 D.m<1
【分析】要使一元二次方程x2+2x﹣m=0有实数根,只需△≥0.
解:∵一元二次方程x2+2x﹣m=0有实数根,
∴Δ=4+4m≥0,
即m≥﹣1.
故选:A.
9.如图,EF是△ABC纸片的中位线,将△AEF沿EF所在的直线折叠,点A落在BC边上的点D处,已知△AEF的面积为7,则图中阴影部分的面积为( )
A.7 B.14 C.21 D.28
【分析】根据三角形的中位线定理,结合相似三角形的性质可以求得△ABC的面积,再根据折叠的性质得到△DEF的面积,从而求解.
解:∵EF是△ABC的中位线,
∴EF∥BC,EF=BC.
∴△AEF∽△ACB.
∴==()2=.
∴△ABC的面积=28.
由折叠的性质得△DEF的面积为7,
∴图中阴影部分的面积为28﹣7﹣7=14.
故选:B.
10.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
A.88° B.92° C.106° D.136°
【分析】首先根据∠BOD=88°,应用圆周角定理,求出∠BAD的度数多少;然后根据圆内接四边形的性质,可得∠BAD+∠BCD=180°,据此求出∠BCD的度数是多少即可.
解:∵∠BOD=88°,
∴∠BAD=88°÷2=44°,
∵∠BAD+∠BCD=180°,
∴∠BCD=180°﹣44°=136°,
即∠BCD的度数是136°.
故选:D.
11.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于( )
A.3 B. C.2 D.
【分析】设正六边形的边长为a,求出BH长,根据正切值算出BH与AB的比即可.
解:连接BD,如图所示:
由正六边形和正方形的性质得:B、D、H三点共线,
设正六边形的边长为a,则AB=BC=CD=DE=a,
∵在△BCD中,BC=CD=a,∠BCD=120°,
∴BD=a.
∴BH=DB+DH=(+1)a.
在Rt△ABH中,tan∠HAB==+1.
故选:B.
12.已知x2﹣4x﹣1=0,则代数式﹣的值是( )
A.7 B.6 C.5 D.﹣5
【分析】原式通分并利用同分母分式的减法法则计算,把已知等式变形后代入计算即可求出值.
解:原式=
=
=
由x2﹣4x﹣1=0,得到x2﹣4x=1,即x(x﹣4)=1,(x﹣2)2=5,
则原式=5,
故选:C.
13.如图是反比例函数y=和y=﹣在x轴上方的图象,x轴的平行线AB分别与这两个函数图象相交于点A,B,点P在x轴上.则点P从左到右的运动过程中,△APB的面积是( )
A.10 B.4
C.5 D.从小变大再变小
【分析】利用反比例函数的比例系数的几何意义即可得到答案.
解:连接OA、OB,
∵x轴的平行线AB分别与这两个函数图象相交于点A,B.设AB交y轴于C.
∴AB⊥y轴,
∵点A、B在反比例函数y=和y=﹣在x轴上方的图象上,
∴S△PAB=S△AOB=S△COB+S△AOC=(3+7)=5,
故选:C.
二、填空题(每小题3分)
14.分解因式:ax2﹣4a= a(x+2)(x﹣2) .
【分析】先提取公因式a,再对余下的多项式利用平方差公式继续分解.
解:ax2﹣4a,
=a(x2﹣4),
=a(x+2)(x﹣2).
15.不等式﹣3<0的最大整数解是 x=4 .
【分析】求出不等式的解集,找出解集中的最大整数即可.
解:由不等式﹣3<0解得:x<5,
则不等式的最大整数解是x=4.
故答案为:x=4.
16.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为 20 km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为 13 km.
【分析】(1)由垂线段最短以及根据两点的纵坐标相同即可求出AB的长度;
(2)根据A、B、C三点的坐标可求出CE与AE的长度,设CD=x,根据勾股定理即可求出x的值.
解:(1)由A、B两点的纵坐标相同可知:AB∥x轴,
∴AB=12﹣(﹣8)=20;
(2)过点C作l⊥AB于点E,连接AC,作AC的垂直平分线交直线l于点D,
由(1)可知:CE=1﹣(﹣17)=18,
AE=12,
设CD=x,
∴AD=CD=x,
由勾股定理可知:x2=(18﹣x)2+122,
∴解得:x=13,
∴CD=13,
故答案为:(1)20;(2)13;
三、解答题(共52分)
17.某书店新进了一批图书,甲、乙两种书的进价分别为4元/本、10元/本.现购进m本甲种书和n本乙种书,共付款Q元.
(1)用含m,n的代数式表示Q;
(2)若共购进5×104本甲种书及3×103本乙种书,用科学记数法表示Q的值.
【分析】(1)分析题目,弄懂题意即可根据题意列出代数式;
(2)根据(1)式的代数式将数字代入,再用科学记数法表示出即可.
解:(1)由题意可得:Q=4m+10n;
(2)将m=5×104,n=3×103代入(1)式得:
Q=4×5×104+10×3×103=2.3×105.
18.已知训练场球筐中有A、B两种品牌的乒乓球共101个,设A品牌乒乓球有x个.
(1)淇淇说:“筐里B品牌球是A品牌球的两倍.”嘉嘉根据她的说法列出了方程:101﹣x=2x.请用嘉嘉所列方程分析淇淇的说法是否正确;
(2)据工作人员透露:B品牌球比A品牌球至少多28个,试通过列不等式的方法说明A品牌球最多有几个.
【分析】(1)解嘉嘉所列的方程可得出x的值,由x的值不为整数,即可得出淇淇的说法不正确;
(2)设A品牌乒乓球有x个,则B品牌乒乓球有(101﹣x)个,根据B品牌球比A品牌球至少多28个,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,再取其中的最大整数值即可得出结论.
解:(1)嘉嘉所列方程为101﹣x=2x,
解得:x=33,
又∵x为整数,
∴x=33不合题意,
∴淇淇的说法不正确.
(2)设A品牌乒乓球有x个,则B品牌乒乓球有(101﹣x)个,
依题意得:101﹣x﹣x≥28,
解得:x≤36,
又∵x为整数,
∴x可取的最大值为36.
答:A品牌球最多有36个.
19.不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,现从中任意摸出一个是红球的概率为.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率.
【分析】(1)根据红球的概率为及红球个数求出所有球的个数,然后利用概率公式解答即可.
(2)此题需要两步完成,所以采用树状图法或者采用列表法都比较简单;解题时要注意是放回实验还是不放回实验,此题属于不放回实验.
解:(1)设袋中黄球的个数为x个,
∴袋中黄球的个数为1个;
(2)、列表如下:
* 红1 红2 黄 蓝
红1 * (红1,红2) (红1,黄) (红1,蓝)
红2 (红2,红1) * (红2,黄) (红2,蓝)
黄 (黄,红1) (黄,红2) * (黄,蓝)
蓝 (蓝,红1) (蓝,红2) (蓝,黄) *
∴一共有12种情况,两次摸到都是红球的有2种情况,
∴两次摸到都是红球的概率为:P=
20.小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,如图所示,图中的线段y1、y2分别表示小东、小明离B地的距离y1、y2(千米)与所用时间x(小时)的关系.
(1)写出y1、y2与x的关系式: y1=﹣5x+20 , y2=3x ;
(2)试用文字说明:交点P所表示的实际意义.
(3)试求出A、B两地之间的距离.
(4)求出小东、小明相距4千米时出发的时间.
【分析】(1)需求直线y1的解析式,因为它过点(2.5,7.5),(4,0),利用待定系数法即可求出其解析式.再利用待定系数法即可求出OP的解析式;
(2)因为小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,所以交点P(2.5,7.5)的意义是经过2.5小时后,小东与小明在距离B地7.5千米处相遇;
(3)需求直线y1的解析式,因为它过点(2.5,7.5),(4,0),利用待定系数法即可求出其解析式.然后令x=0,求出此时的y值即可;
(4)根据题意列方程解答即可.
解:(1)设y1=k1x+b,根据题意得:
,解得,
∴y1=﹣5x+20,
设y2=k2x,根据题意得:2.5k2=7.5,解得k2=3,
∴y2=3x.
故答案为:y1=﹣5x+20,y2=3x.
(2)交点P所表示的实际意义是:
经过2.5小时后,小东与小明在距离B地7.5千米处相遇.
(3)y1=﹣5x+20,当x=0时,y1=20.
故AB两地之间的距离为20千米.
(4)根据题意得5x+3x=20﹣4或5x+3x=20+4,
解得x=2或x=3.
即出发2小时或3小时小东、小明相距4千米.
21.如图,在△ABC中,∠BAC=90°,∠B=60°,AB=2.AD⊥BC于D.E为边BC上的一个(不与B、C重合)点,且AE⊥EF于E,∠EAF=∠B,EF、AF相交于点F.
(1)填空:AC= 2 ;∠F= 30° .
(2)当BD=DE时,证明:△ABC≌△EAF.
(3)△EAF面积的最小值是 .
(4)当△EAF的内心在△ABC的外部时,直接写出AE的范围 .
【分析】(1)先解直角三角形ABC,求得AC的值,再在直角三角形AEF中,利用互余关系求得∠F即可;
(2)先利用等腰三角形的“三线合一“性质证明AB=AE,再利用ASA证明△ABC≌△EAF;
(3))先在△AEF中,由三角函数求得EF=AE,再利用三角形的面积公式得出S△EAF=AE2,然后由当AE⊥BC时,AE最短,S△EAF最小,求得AE的值,则△EAF面积的最小值可得;
(4)当△EAF内心恰好落在AC上时,设△EAF的内心为N,连接EN,利用三角形的内心性质证明△ABE是等边三角形,从而可知AE=AB=2,由(1)可知AC=2,从而可得当△EAF的内心在△ABC的外部时,AE的范围.
解:(1)∵∠BAC=90°,∠B=60°,AB=2,tanB=,
∴AC=AB tanB=2tan60°=2;
∵AE⊥EF,
∴∠AEF=90°,
∵∠EAF=∠B=60°,
∴∠F=90°﹣∠EAF=90°﹣60°=30°.
故答案为:2,30°;
(2)证明:当BD=DE时,
∵AD⊥BC于D,
∴AB=AE,
∵∠AEF=90°,∠BAC=90°,
∴∠AEF=∠BAC,
又∠EAF=∠B,
∴△ABC≌△EAF(ASA);
(3)∵∠AEF=90°,∠EAF=60°,tan∠EAF=,
∴EF=AE tan∠EAF=AE tan60°=AE,
∴S△EAF=AE EF=AE×AE=AE2,
当AE⊥BC时,AE最短,S△EAF最小,此时∠AEB=90°,sinB=,
∴AE=AB sinB=2sin60°=2×=,
S△EAF=AE2=×3=,
∴△EAF面积的最小值是,
故答案为:;
(4)当△EAF内心恰好落在AC上时,设△EAF的内心为N,连接EN,如图:
∵N是△EAF的内心,
∴AN平分∠EAF,EN平分∠AEF,
∴∠EAC=∠EAF=×60°=30°,
∵∠BAC=90°,
∴∠BAE=∠BAC﹣∠EAC=90°﹣30°=60°,
又∵∠B=60°,
∴△ABE是等边三角形,
∴AE=AB=2,
∵E为BC上的一点,不与B、C重合,由(1)可知AC=2,
∴当△EAF的内心在△ABC的外部时,.
故答案为:.
22.如图是某同学正在设计的一动画示意图,x轴上依次有A,O,N三个点,且AO=2,在ON上方有五个台阶T1~T5(各拐角均为90°),每个台阶的高、宽分别是1和1.5,台阶T1到x轴距离OK=10.从点A处向右上方沿抛物线L:y=﹣x2+4x+12发出一个带光的点P.
(1)求点A的横坐标,且在图中补画出y轴,并直接指出点P会落在哪个台阶上;
(2)当点P落到台阶上后立即弹起,又形成了另一条与L形状相同的抛物线C,且最大高度为11,求C的解析式,并说明其对称轴是否与台阶T5有交点;
(3)在x轴上从左到右有两点D,E,且DE=1,从点E向上作EB⊥x轴,且BE=2.在△BDE沿x轴左右平移时,必须保证(2)中沿抛物线C下落的点P能落在边BD(包括端点)上,则点B横坐标的最大值比最小值大多少?
[注:(2)中不必写x的取值范围]
【分析】(1)由题意台阶T4的左边端点(4.5,7),右边端点的坐标(6,7),求出x=4.5,6时的y的值,即可判断.
(2)由题意抛物线C:y=﹣x2+bx+c,经过R(5,7),最高点的纵坐标为11,构建方程组求出b,c,可得结论.
(3)求出抛物线与X轴的交点,以及y=2时,点的坐标,判断出两种特殊位置点B的横坐标的值,可得结论.
解:(1)图形如图所示,由题意台阶T4左边的端点坐标(4.5,7),右边的端点(6,7),
对于抛物线y=﹣x2+4x+12,
令y=0,x2﹣4x﹣12=0,解得x=﹣2或6,
∴A(﹣2,0),
∴点A的横坐标为﹣2,
当x=4.5时,y=9.75>7,
当x=6时,y=0<7,
当y=7时,7=﹣x2+4x+12,
解得x=﹣1或5,
∴抛物线与台阶T4有交点,设交点为R(5,7),
∴点P会落在台阶T4上.
(2)由题意抛物线C:y=﹣x2+bx+c,经过R(5,7),最高点的纵坐标为11,
∴,
解得或(舍弃),
∴抛物线C的解析式为y=﹣x2+14x﹣38,
对称轴x=7,
∵台阶T5的左边的端点(6,6),右边的端点为(7.5,6),
∴抛物线C的对称轴与台阶T5有交点.
(3)对于抛物线C:y=﹣x2+14x﹣38,
令y=0,得到x2﹣14x+38=0,解得x=7±,
∴抛物线C交x轴的正半轴于(7+,0),
当y=2时,2=﹣x2+14x﹣38,解得x=4或10,
∴抛物线经过(10,2),
Rt△BDE中,∠DEB=90°,DE=1,BE=2,
∴当点D与(7+,0)重合时,点B的横坐标的值最大,最大值为8+,
当点B与(10,2)重合时,点B的横坐标最小,最小值为10,
∴点B横坐标的最大值比最小值大﹣2.
一、选择题(每小题3分)
1.下列各数中,最小的数是( )
A.0 B.1 C.﹣1 D.﹣
2.计算:﹣a2+2a2=( )
A.a2 B.﹣a2 C.2a2 D.0
3.如图是五个相同的小正方体搭成的几何体,其俯视图是( )
A. B.
C. D.
4.PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,是衡量空气污染程度的重要指标.将0.0000025用科学记数法表示为2.5×10n,则n的值是( )
A.﹣5 B.﹣6 C.﹣7 D.﹣8
5.如图,∠1=30°,∠B=60°,AB⊥AC,则下列说法正确的是( )
A.AB∥CD B.AD∥BC
C.AC⊥CD D.∠DAB+∠D=180°
6.已知(x﹣1)3=ax3+bx2+cx+d,则a+b+c+d的值为( )
A.﹣1 B.0 C.1 D.不能确定
7.如图,在直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是﹣1,则菱形OACB的边长为( )
A.3 B. C.5 D.
8.如果关于x的一元二次方程x2+2x﹣m=0有实数根,则m的取值范围是( )
A.m≥﹣1 B.m≤﹣1 C.m>1 D.m<1
9.如图,EF是△ABC纸片的中位线,将△AEF沿EF所在的直线折叠,点A落在BC边上的点D处,已知△AEF的面积为7,则图中阴影部分的面积为( )
A.7 B.14 C.21 D.28
10.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
A.88° B.92° C.106° D.136°
11.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于( )
A.3 B. C.2 D.
12.已知x2﹣4x﹣1=0,则代数式﹣的值是( )
A.7 B.6 C.5 D.﹣5
13.如图是反比例函数y=和y=﹣在x轴上方的图象,x轴的平行线AB分别与这两个函数图象相交于点A,B,点P在x轴上.则点P从左到右的运动过程中,△APB的面积是( )
A.10 B.4
C.5 D.从小变大再变小
二、填空题(每小题3分)
14.分解因式:ax2﹣4a= .
15.不等式﹣3<0的最大整数解是 .
16.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为 km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为 km.
三、解答题(共52分)
17.某书店新进了一批图书,甲、乙两种书的进价分别为4元/本、10元/本.现购进m本甲种书和n本乙种书,共付款Q元.
(1)用含m,n的代数式表示Q;
(2)若共购进5×104本甲种书及3×103本乙种书,用科学记数法表示Q的值.
18.已知训练场球筐中有A、B两种品牌的乒乓球共101个,设A品牌乒乓球有x个.
(1)淇淇说:“筐里B品牌球是A品牌球的两倍.”嘉嘉根据她的说法列出了方程:101﹣x=2x.请用嘉嘉所列方程分析淇淇的说法是否正确;
(2)据工作人员透露:B品牌球比A品牌球至少多28个,试通过列不等式的方法说明A品牌球最多有几个.
19.不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,现从中任意摸出一个是红球的概率为.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率.
20.小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,如图所示,图中的线段y1、y2分别表示小东、小明离B地的距离y1、y2(千米)与所用时间x(小时)的关系.
(1)写出y1、y2与x的关系式: , ;
(2)试用文字说明:交点P所表示的实际意义.
(3)试求出A、B两地之间的距离.
(4)求出小东、小明相距4千米时出发的时间.
21.如图,在△ABC中,∠BAC=90°,∠B=60°,AB=2.AD⊥BC于D.E为边BC上的一个(不与B、C重合)点,且AE⊥EF于E,∠EAF=∠B,EF、AF相交于点F.
(1)填空:AC= ;∠F= .
(2)当BD=DE时,证明:△ABC≌△EAF.
(3)△EAF面积的最小值是 .
(4)当△EAF的内心在△ABC的外部时,直接写出AE的范围 .
22.如图是某同学正在设计的一动画示意图,x轴上依次有A,O,N三个点,且AO=2,在ON上方有五个台阶T1~T5(各拐角均为90°),每个台阶的高、宽分别是1和1.5,台阶T1到x轴距离OK=10.从点A处向右上方沿抛物线L:y=﹣x2+4x+12发出一个带光的点P.
(1)求点A的横坐标,且在图中补画出y轴,并直接指出点P会落在哪个台阶上;
(2)当点P落到台阶上后立即弹起,又形成了另一条与L形状相同的抛物线C,且最大高度为11,求C的解析式,并说明其对称轴是否与台阶T5有交点;
(3)在x轴上从左到右有两点D,E,且DE=1,从点E向上作EB⊥x轴,且BE=2.在△BDE沿x轴左右平移时,必须保证(2)中沿抛物线C下落的点P能落在边BD(包括端点)上,则点B横坐标的最大值比最小值大多少?
[注:(2)中不必写x的取值范围]
参考答案
一、选择题(每小题3分)
1.下列各数中,最小的数是( )
A.0 B.1 C.﹣1 D.﹣
【分析】根据正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,进行比较.
解:∵正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,
∴﹣<﹣1<0<1,
故选:D.
2.计算:﹣a2+2a2=( )
A.a2 B.﹣a2 C.2a2 D.0
【分析】根据合并同类项法则,合并同类项时,系数相加减,字母及其指数不变,据此计算即可得出正确选项.
解:﹣a2+2a2=(﹣1+2)a2=a2,
故选:A.
3.如图是五个相同的小正方体搭成的几何体,其俯视图是( )
A. B.
C. D.
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
解:如图是五个相同的小正方体搭成的几何体,其俯视图是.
故选:C.
4.PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,是衡量空气污染程度的重要指标.将0.0000025用科学记数法表示为2.5×10n,则n的值是( )
A.﹣5 B.﹣6 C.﹣7 D.﹣8
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.0000025=2.5×10﹣6,
∴n=﹣6.
故选:B.
5.如图,∠1=30°,∠B=60°,AB⊥AC,则下列说法正确的是( )
A.AB∥CD B.AD∥BC
C.AC⊥CD D.∠DAB+∠D=180°
【分析】因为AB⊥AC,所以∠BAC=90°,又因为∠1=30°,∠B=60°,则可求得∠1=∠BCA=30°,故AD∥BC.
解:∵AB⊥AC,
∴∠BAC=90°.
∵∠1=30°,∠B=60°,
∴∠BCA=30°.
∴∠1=∠BCA.
∴AD∥BC.
故选:B.
6.已知(x﹣1)3=ax3+bx2+cx+d,则a+b+c+d的值为( )
A.﹣1 B.0 C.1 D.不能确定
【分析】令x=1,即可求出原式的值.
解:把x=1代入(x﹣1)3=ax3+bx2+cx+d,
得a+b+c+d=0.
故选:B.
7.如图,在直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是﹣1,则菱形OACB的边长为( )
A.3 B. C.5 D.
【分析】首先连接AB交OC于点D,由菱形OACB中,点C的坐标是(4,0),点B的纵坐标是﹣1,即可求得菱形OACB的边长.
解:连接AB交OC于点D,
∵四边形ABCD是菱形,
∴AB⊥OC,OD=CD,AD=BD,
∵点C的坐标是(4,0),点B的纵坐标是﹣1,
∴OC=4,BD=AD=1,
∴OD=CD=2,
∴菱形OACB的边长为=.
故选:D.
8.如果关于x的一元二次方程x2+2x﹣m=0有实数根,则m的取值范围是( )
A.m≥﹣1 B.m≤﹣1 C.m>1 D.m<1
【分析】要使一元二次方程x2+2x﹣m=0有实数根,只需△≥0.
解:∵一元二次方程x2+2x﹣m=0有实数根,
∴Δ=4+4m≥0,
即m≥﹣1.
故选:A.
9.如图,EF是△ABC纸片的中位线,将△AEF沿EF所在的直线折叠,点A落在BC边上的点D处,已知△AEF的面积为7,则图中阴影部分的面积为( )
A.7 B.14 C.21 D.28
【分析】根据三角形的中位线定理,结合相似三角形的性质可以求得△ABC的面积,再根据折叠的性质得到△DEF的面积,从而求解.
解:∵EF是△ABC的中位线,
∴EF∥BC,EF=BC.
∴△AEF∽△ACB.
∴==()2=.
∴△ABC的面积=28.
由折叠的性质得△DEF的面积为7,
∴图中阴影部分的面积为28﹣7﹣7=14.
故选:B.
10.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
A.88° B.92° C.106° D.136°
【分析】首先根据∠BOD=88°,应用圆周角定理,求出∠BAD的度数多少;然后根据圆内接四边形的性质,可得∠BAD+∠BCD=180°,据此求出∠BCD的度数是多少即可.
解:∵∠BOD=88°,
∴∠BAD=88°÷2=44°,
∵∠BAD+∠BCD=180°,
∴∠BCD=180°﹣44°=136°,
即∠BCD的度数是136°.
故选:D.
11.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于( )
A.3 B. C.2 D.
【分析】设正六边形的边长为a,求出BH长,根据正切值算出BH与AB的比即可.
解:连接BD,如图所示:
由正六边形和正方形的性质得:B、D、H三点共线,
设正六边形的边长为a,则AB=BC=CD=DE=a,
∵在△BCD中,BC=CD=a,∠BCD=120°,
∴BD=a.
∴BH=DB+DH=(+1)a.
在Rt△ABH中,tan∠HAB==+1.
故选:B.
12.已知x2﹣4x﹣1=0,则代数式﹣的值是( )
A.7 B.6 C.5 D.﹣5
【分析】原式通分并利用同分母分式的减法法则计算,把已知等式变形后代入计算即可求出值.
解:原式=
=
=
由x2﹣4x﹣1=0,得到x2﹣4x=1,即x(x﹣4)=1,(x﹣2)2=5,
则原式=5,
故选:C.
13.如图是反比例函数y=和y=﹣在x轴上方的图象,x轴的平行线AB分别与这两个函数图象相交于点A,B,点P在x轴上.则点P从左到右的运动过程中,△APB的面积是( )
A.10 B.4
C.5 D.从小变大再变小
【分析】利用反比例函数的比例系数的几何意义即可得到答案.
解:连接OA、OB,
∵x轴的平行线AB分别与这两个函数图象相交于点A,B.设AB交y轴于C.
∴AB⊥y轴,
∵点A、B在反比例函数y=和y=﹣在x轴上方的图象上,
∴S△PAB=S△AOB=S△COB+S△AOC=(3+7)=5,
故选:C.
二、填空题(每小题3分)
14.分解因式:ax2﹣4a= a(x+2)(x﹣2) .
【分析】先提取公因式a,再对余下的多项式利用平方差公式继续分解.
解:ax2﹣4a,
=a(x2﹣4),
=a(x+2)(x﹣2).
15.不等式﹣3<0的最大整数解是 x=4 .
【分析】求出不等式的解集,找出解集中的最大整数即可.
解:由不等式﹣3<0解得:x<5,
则不等式的最大整数解是x=4.
故答案为:x=4.
16.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为 20 km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为 13 km.
【分析】(1)由垂线段最短以及根据两点的纵坐标相同即可求出AB的长度;
(2)根据A、B、C三点的坐标可求出CE与AE的长度,设CD=x,根据勾股定理即可求出x的值.
解:(1)由A、B两点的纵坐标相同可知:AB∥x轴,
∴AB=12﹣(﹣8)=20;
(2)过点C作l⊥AB于点E,连接AC,作AC的垂直平分线交直线l于点D,
由(1)可知:CE=1﹣(﹣17)=18,
AE=12,
设CD=x,
∴AD=CD=x,
由勾股定理可知:x2=(18﹣x)2+122,
∴解得:x=13,
∴CD=13,
故答案为:(1)20;(2)13;
三、解答题(共52分)
17.某书店新进了一批图书,甲、乙两种书的进价分别为4元/本、10元/本.现购进m本甲种书和n本乙种书,共付款Q元.
(1)用含m,n的代数式表示Q;
(2)若共购进5×104本甲种书及3×103本乙种书,用科学记数法表示Q的值.
【分析】(1)分析题目,弄懂题意即可根据题意列出代数式;
(2)根据(1)式的代数式将数字代入,再用科学记数法表示出即可.
解:(1)由题意可得:Q=4m+10n;
(2)将m=5×104,n=3×103代入(1)式得:
Q=4×5×104+10×3×103=2.3×105.
18.已知训练场球筐中有A、B两种品牌的乒乓球共101个,设A品牌乒乓球有x个.
(1)淇淇说:“筐里B品牌球是A品牌球的两倍.”嘉嘉根据她的说法列出了方程:101﹣x=2x.请用嘉嘉所列方程分析淇淇的说法是否正确;
(2)据工作人员透露:B品牌球比A品牌球至少多28个,试通过列不等式的方法说明A品牌球最多有几个.
【分析】(1)解嘉嘉所列的方程可得出x的值,由x的值不为整数,即可得出淇淇的说法不正确;
(2)设A品牌乒乓球有x个,则B品牌乒乓球有(101﹣x)个,根据B品牌球比A品牌球至少多28个,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,再取其中的最大整数值即可得出结论.
解:(1)嘉嘉所列方程为101﹣x=2x,
解得:x=33,
又∵x为整数,
∴x=33不合题意,
∴淇淇的说法不正确.
(2)设A品牌乒乓球有x个,则B品牌乒乓球有(101﹣x)个,
依题意得:101﹣x﹣x≥28,
解得:x≤36,
又∵x为整数,
∴x可取的最大值为36.
答:A品牌球最多有36个.
19.不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,现从中任意摸出一个是红球的概率为.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率.
【分析】(1)根据红球的概率为及红球个数求出所有球的个数,然后利用概率公式解答即可.
(2)此题需要两步完成,所以采用树状图法或者采用列表法都比较简单;解题时要注意是放回实验还是不放回实验,此题属于不放回实验.
解:(1)设袋中黄球的个数为x个,
∴袋中黄球的个数为1个;
(2)、列表如下:
* 红1 红2 黄 蓝
红1 * (红1,红2) (红1,黄) (红1,蓝)
红2 (红2,红1) * (红2,黄) (红2,蓝)
黄 (黄,红1) (黄,红2) * (黄,蓝)
蓝 (蓝,红1) (蓝,红2) (蓝,黄) *
∴一共有12种情况,两次摸到都是红球的有2种情况,
∴两次摸到都是红球的概率为:P=
20.小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,如图所示,图中的线段y1、y2分别表示小东、小明离B地的距离y1、y2(千米)与所用时间x(小时)的关系.
(1)写出y1、y2与x的关系式: y1=﹣5x+20 , y2=3x ;
(2)试用文字说明:交点P所表示的实际意义.
(3)试求出A、B两地之间的距离.
(4)求出小东、小明相距4千米时出发的时间.
【分析】(1)需求直线y1的解析式,因为它过点(2.5,7.5),(4,0),利用待定系数法即可求出其解析式.再利用待定系数法即可求出OP的解析式;
(2)因为小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,所以交点P(2.5,7.5)的意义是经过2.5小时后,小东与小明在距离B地7.5千米处相遇;
(3)需求直线y1的解析式,因为它过点(2.5,7.5),(4,0),利用待定系数法即可求出其解析式.然后令x=0,求出此时的y值即可;
(4)根据题意列方程解答即可.
解:(1)设y1=k1x+b,根据题意得:
,解得,
∴y1=﹣5x+20,
设y2=k2x,根据题意得:2.5k2=7.5,解得k2=3,
∴y2=3x.
故答案为:y1=﹣5x+20,y2=3x.
(2)交点P所表示的实际意义是:
经过2.5小时后,小东与小明在距离B地7.5千米处相遇.
(3)y1=﹣5x+20,当x=0时,y1=20.
故AB两地之间的距离为20千米.
(4)根据题意得5x+3x=20﹣4或5x+3x=20+4,
解得x=2或x=3.
即出发2小时或3小时小东、小明相距4千米.
21.如图,在△ABC中,∠BAC=90°,∠B=60°,AB=2.AD⊥BC于D.E为边BC上的一个(不与B、C重合)点,且AE⊥EF于E,∠EAF=∠B,EF、AF相交于点F.
(1)填空:AC= 2 ;∠F= 30° .
(2)当BD=DE时,证明:△ABC≌△EAF.
(3)△EAF面积的最小值是 .
(4)当△EAF的内心在△ABC的外部时,直接写出AE的范围 .
【分析】(1)先解直角三角形ABC,求得AC的值,再在直角三角形AEF中,利用互余关系求得∠F即可;
(2)先利用等腰三角形的“三线合一“性质证明AB=AE,再利用ASA证明△ABC≌△EAF;
(3))先在△AEF中,由三角函数求得EF=AE,再利用三角形的面积公式得出S△EAF=AE2,然后由当AE⊥BC时,AE最短,S△EAF最小,求得AE的值,则△EAF面积的最小值可得;
(4)当△EAF内心恰好落在AC上时,设△EAF的内心为N,连接EN,利用三角形的内心性质证明△ABE是等边三角形,从而可知AE=AB=2,由(1)可知AC=2,从而可得当△EAF的内心在△ABC的外部时,AE的范围.
解:(1)∵∠BAC=90°,∠B=60°,AB=2,tanB=,
∴AC=AB tanB=2tan60°=2;
∵AE⊥EF,
∴∠AEF=90°,
∵∠EAF=∠B=60°,
∴∠F=90°﹣∠EAF=90°﹣60°=30°.
故答案为:2,30°;
(2)证明:当BD=DE时,
∵AD⊥BC于D,
∴AB=AE,
∵∠AEF=90°,∠BAC=90°,
∴∠AEF=∠BAC,
又∠EAF=∠B,
∴△ABC≌△EAF(ASA);
(3)∵∠AEF=90°,∠EAF=60°,tan∠EAF=,
∴EF=AE tan∠EAF=AE tan60°=AE,
∴S△EAF=AE EF=AE×AE=AE2,
当AE⊥BC时,AE最短,S△EAF最小,此时∠AEB=90°,sinB=,
∴AE=AB sinB=2sin60°=2×=,
S△EAF=AE2=×3=,
∴△EAF面积的最小值是,
故答案为:;
(4)当△EAF内心恰好落在AC上时,设△EAF的内心为N,连接EN,如图:
∵N是△EAF的内心,
∴AN平分∠EAF,EN平分∠AEF,
∴∠EAC=∠EAF=×60°=30°,
∵∠BAC=90°,
∴∠BAE=∠BAC﹣∠EAC=90°﹣30°=60°,
又∵∠B=60°,
∴△ABE是等边三角形,
∴AE=AB=2,
∵E为BC上的一点,不与B、C重合,由(1)可知AC=2,
∴当△EAF的内心在△ABC的外部时,.
故答案为:.
22.如图是某同学正在设计的一动画示意图,x轴上依次有A,O,N三个点,且AO=2,在ON上方有五个台阶T1~T5(各拐角均为90°),每个台阶的高、宽分别是1和1.5,台阶T1到x轴距离OK=10.从点A处向右上方沿抛物线L:y=﹣x2+4x+12发出一个带光的点P.
(1)求点A的横坐标,且在图中补画出y轴,并直接指出点P会落在哪个台阶上;
(2)当点P落到台阶上后立即弹起,又形成了另一条与L形状相同的抛物线C,且最大高度为11,求C的解析式,并说明其对称轴是否与台阶T5有交点;
(3)在x轴上从左到右有两点D,E,且DE=1,从点E向上作EB⊥x轴,且BE=2.在△BDE沿x轴左右平移时,必须保证(2)中沿抛物线C下落的点P能落在边BD(包括端点)上,则点B横坐标的最大值比最小值大多少?
[注:(2)中不必写x的取值范围]
【分析】(1)由题意台阶T4的左边端点(4.5,7),右边端点的坐标(6,7),求出x=4.5,6时的y的值,即可判断.
(2)由题意抛物线C:y=﹣x2+bx+c,经过R(5,7),最高点的纵坐标为11,构建方程组求出b,c,可得结论.
(3)求出抛物线与X轴的交点,以及y=2时,点的坐标,判断出两种特殊位置点B的横坐标的值,可得结论.
解:(1)图形如图所示,由题意台阶T4左边的端点坐标(4.5,7),右边的端点(6,7),
对于抛物线y=﹣x2+4x+12,
令y=0,x2﹣4x﹣12=0,解得x=﹣2或6,
∴A(﹣2,0),
∴点A的横坐标为﹣2,
当x=4.5时,y=9.75>7,
当x=6时,y=0<7,
当y=7时,7=﹣x2+4x+12,
解得x=﹣1或5,
∴抛物线与台阶T4有交点,设交点为R(5,7),
∴点P会落在台阶T4上.
(2)由题意抛物线C:y=﹣x2+bx+c,经过R(5,7),最高点的纵坐标为11,
∴,
解得或(舍弃),
∴抛物线C的解析式为y=﹣x2+14x﹣38,
对称轴x=7,
∵台阶T5的左边的端点(6,6),右边的端点为(7.5,6),
∴抛物线C的对称轴与台阶T5有交点.
(3)对于抛物线C:y=﹣x2+14x﹣38,
令y=0,得到x2﹣14x+38=0,解得x=7±,
∴抛物线C交x轴的正半轴于(7+,0),
当y=2时,2=﹣x2+14x﹣38,解得x=4或10,
∴抛物线经过(10,2),
Rt△BDE中,∠DEB=90°,DE=1,BE=2,
∴当点D与(7+,0)重合时,点B的横坐标的值最大,最大值为8+,
当点B与(10,2)重合时,点B的横坐标最小,最小值为10,
∴点B横坐标的最大值比最小值大﹣2.
同课章节目录
