人教版数学八年级下册 16.3.1二次根式的加减 课件(共15张PPT)
文档属性
| 名称 | 人教版数学八年级下册 16.3.1二次根式的加减 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 184.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 19:43:48 | ||
图片预览






文档简介
(共15张PPT)
16.3(1) 二次根式的加减
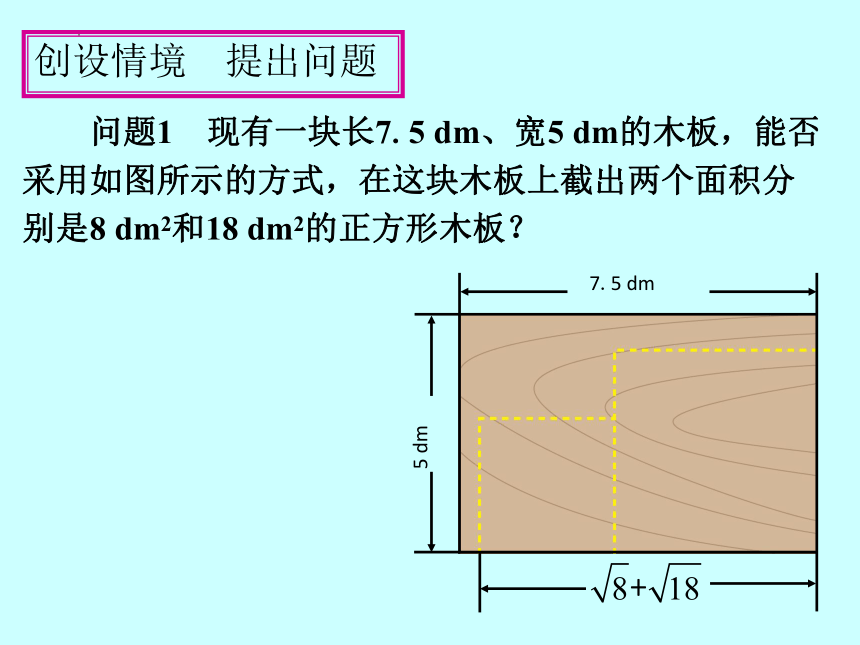
问题1 现有一块长7.5 dm、宽5 dm的木板,能否
采用如图所示的方式,在这块木板上截出两个面积分
别是8 dm2和18 dm2的正方形木板?
创设情境 提出问题
5 dm
7.5 dm
学习目标:
1.探索二次根式加减运算的方法和步骤;
2.会进行二次根式的加减运算.
学习重点:
在化简二次根式的基础上,应用分配律进行二次根式的加减运算.
复习
2. 把下列二次根式化成最简二次根式:
(1) ; (2) ;(3) ;
(4) ; (4) ;(6) .
1.计算:
(1)2x+3x =_____; (2)2x2-3x2+5x2 =_____;
(3)x+2x+3y=______;(4)3a2-2a2+a3 =______.
a2+a3
4x2
3x+3y
5x
同类二次根式
问题1. 观察下列二次根式有何特征?
(1) (2)
被开方数相同
同类二次根式:
的二次根式.
练习:判断下列二次根式是否为同类二次根式.
(1) (2) (3)
问题2:计算.
二次根式的加减
(1)
(2)
(3)
分配律
被开方数相同
1. 合并的依据?
2.什么情况下可以合并?
练:P10 (1)
问题3:计算并写出依据.
二次根式的加减
(4)
化为最简二次根式
分配律
________________
________________
二次根式加减法则:
二次根式加减时,可以先将二次根式化为
最简二次根式 ,再将被开方数相同的二次根式
进行合并。
归纳:
合作探究 形成知识
步骤:
“一化简、二判断、三合并”;
依据:
二次根式的性质、分配律和整式加减法则;
基本思想:
把二次根式加减问题转化为整式加减问题.
请总结二次根式加减的步骤、依据和基本思想.
例1 计算:
(1)
(2)
二次根式的加减
初步应用 巩固知识
例2 计算(并说出运算步骤和每一步的依据):
(1)
(2) .
练习2 P13 ::2,3
问题1 现有一块长7.5 dm、宽5 dm的木板,能否
采用如图所示的方式,在这块木板上截出两个面积分
别是8 dm2和18 dm2的正方形木板?
能截出两块正方形木
板的条件是什么?能用数
学式子表示吗?
5 dm
7.5 dm
5 dm
7.5 dm
如何比较大小:
__ 5
__ 7.5
综合应用 深化提高
练习3 化简: .
解:原式
课堂小结
(1)二次根式的加减运算分哪几步进行?每一个步骤
的依据是什么?
(2)在二次根式的加减中,主要的想法是怎样的?
(3)在二次根式加减中,有哪些地方容易出现错误?
16.3(1) 二次根式的加减
问题1 现有一块长7.5 dm、宽5 dm的木板,能否
采用如图所示的方式,在这块木板上截出两个面积分
别是8 dm2和18 dm2的正方形木板?
创设情境 提出问题
5 dm
7.5 dm
学习目标:
1.探索二次根式加减运算的方法和步骤;
2.会进行二次根式的加减运算.
学习重点:
在化简二次根式的基础上,应用分配律进行二次根式的加减运算.
复习
2. 把下列二次根式化成最简二次根式:
(1) ; (2) ;(3) ;
(4) ; (4) ;(6) .
1.计算:
(1)2x+3x =_____; (2)2x2-3x2+5x2 =_____;
(3)x+2x+3y=______;(4)3a2-2a2+a3 =______.
a2+a3
4x2
3x+3y
5x
同类二次根式
问题1. 观察下列二次根式有何特征?
(1) (2)
被开方数相同
同类二次根式:
的二次根式.
练习:判断下列二次根式是否为同类二次根式.
(1) (2) (3)
问题2:计算.
二次根式的加减
(1)
(2)
(3)
分配律
被开方数相同
1. 合并的依据?
2.什么情况下可以合并?
练:P10 (1)
问题3:计算并写出依据.
二次根式的加减
(4)
化为最简二次根式
分配律
________________
________________
二次根式加减法则:
二次根式加减时,可以先将二次根式化为
最简二次根式 ,再将被开方数相同的二次根式
进行合并。
归纳:
合作探究 形成知识
步骤:
“一化简、二判断、三合并”;
依据:
二次根式的性质、分配律和整式加减法则;
基本思想:
把二次根式加减问题转化为整式加减问题.
请总结二次根式加减的步骤、依据和基本思想.
例1 计算:
(1)
(2)
二次根式的加减
初步应用 巩固知识
例2 计算(并说出运算步骤和每一步的依据):
(1)
(2) .
练习2 P13 ::2,3
问题1 现有一块长7.5 dm、宽5 dm的木板,能否
采用如图所示的方式,在这块木板上截出两个面积分
别是8 dm2和18 dm2的正方形木板?
能截出两块正方形木
板的条件是什么?能用数
学式子表示吗?
5 dm
7.5 dm
5 dm
7.5 dm
如何比较大小:
__ 5
__ 7.5
综合应用 深化提高
练习3 化简: .
解:原式
课堂小结
(1)二次根式的加减运算分哪几步进行?每一个步骤
的依据是什么?
(2)在二次根式的加减中,主要的想法是怎样的?
(3)在二次根式加减中,有哪些地方容易出现错误?
