北师大版七年级数学下册第二章相交线与平行线 复习课件(共54张PPT)
文档属性
| 名称 | 北师大版七年级数学下册第二章相交线与平行线 复习课件(共54张PPT) | 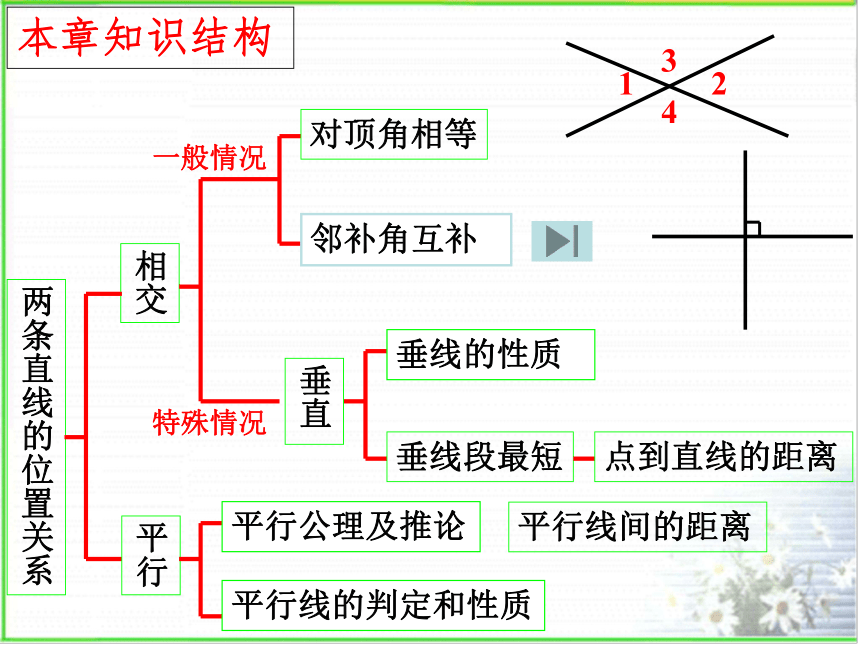 | |
| 格式 | zip | ||
| 文件大小 | 709.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 19:51:45 | ||
图片预览




文档简介
(共54张PPT)
相交
一般情况
特殊情况
对顶角相等
邻补角互补
垂直
垂线段最短
点到直线的距离
1
2
3
4
垂线的性质
本章知识结构
两条直线的位置关系
平行
平行公理及推论
平行线的判定和性质
平行线间的距离
第二章 平行线与相交线
复习课
知识点梳理
1、平行线
在同一平面内,不相交的两条直线叫做平行线。
⑴定义:
⑵平行公理 :经过已知直线外一点,有且只有一条直
线与已知直线平行。
⑶平行公理的推论:
如果两条直线都和第三条直线平行,则这两条直线也互相平行。
平行于同一直线的两直线互相平行
概念、性质填空:
一、概念:
两个角的和是_____,称这两个角互为余角。
两个角的和是平角,称这两个角互为_____。
有公共顶点,两边互为反向延长线的两个
角叫做_______。
二、性质:
_________的余角相等;
同角或等角的____相等;
对顶角_____。
直角
补角
对顶角
同角或等角
补角
相等
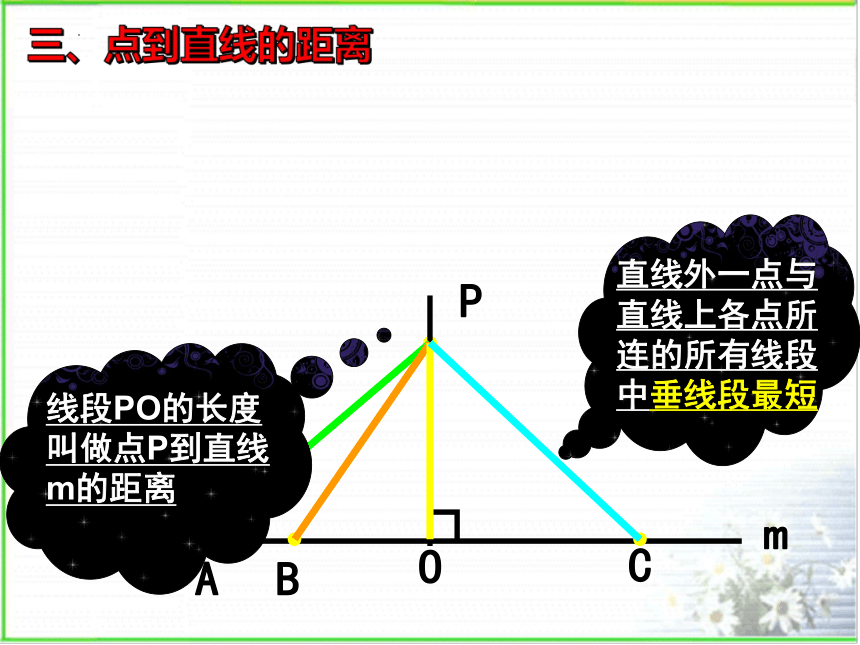
m
P
O
C
B
A
直线外一点与直线上各点所连的所有线段中垂线段最短
线段PO的长度叫做点P到直线m的距离
三、点到直线的距离
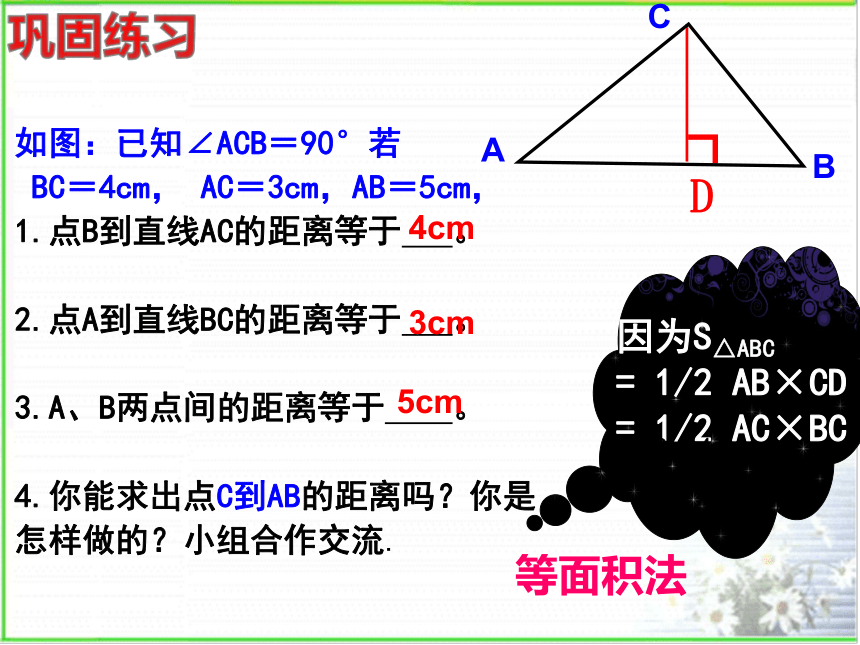
如图:已知∠ACB=90°若
BC=4cm, AC=3cm,AB=5cm, 1.点B到直线AC的距离等于 。
2.点A到直线BC的距离等于 。
3.A、B两点间的距离等于 。
4.你能求出点C到AB的距离吗?你是怎样做的?小组合作交流.
D
因为S△ABC
= 1/2 AB×CD
= 1/2 AC×BC
所以CD=2.4cm
巩固练习
4cm
A
C
B
3cm
5cm
等面积法
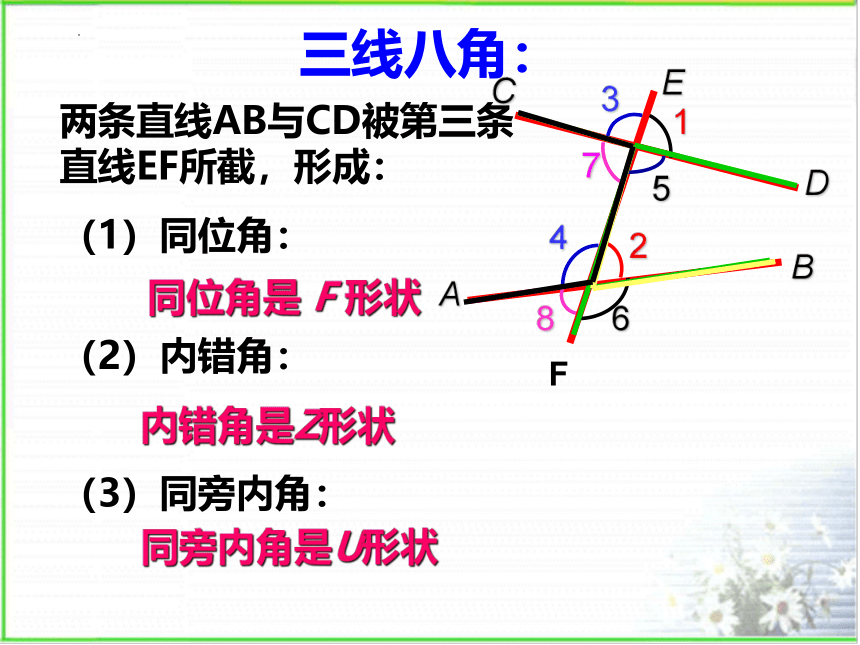
三线八角:
两条直线AB与CD被第三条直线EF所截,形成:
(1)同位角:
(2)内错角:
(3)同旁内角:
同位角是 F 形状
内错角是Z形状
同旁内角是U形状
C
A
1
3
7
5
2
8
6
E
4
D
B
F
区别:条件与结论互换,
即:已知平行用特征,探索平行用判定。
3、平行线的判定方法:
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行;
4、平行线的特征:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
a
b
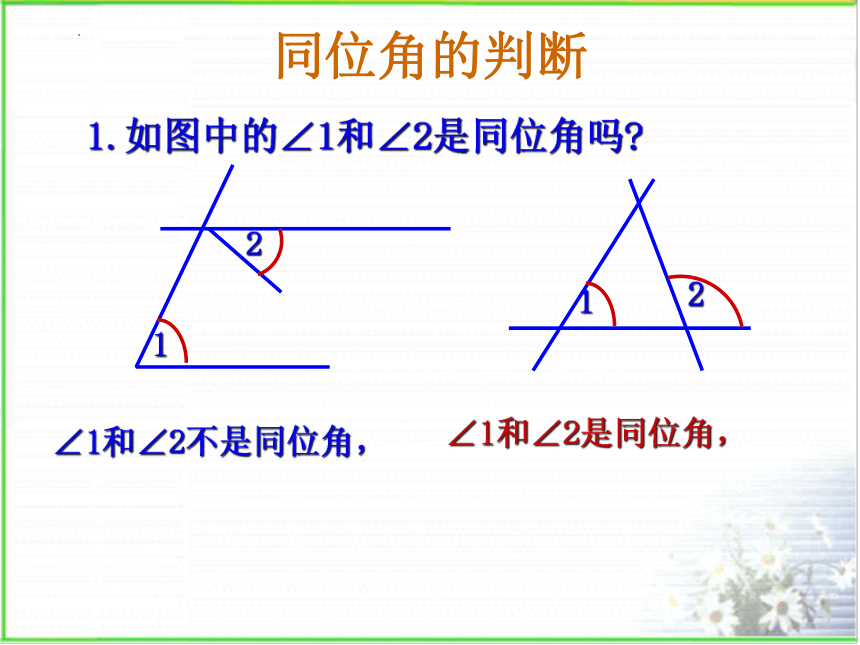
∠1和∠2不是同位角,
同位角的判断
1.如图中的∠1和∠2是同位角吗
1
2
1
2
∠1和∠2是同位角,
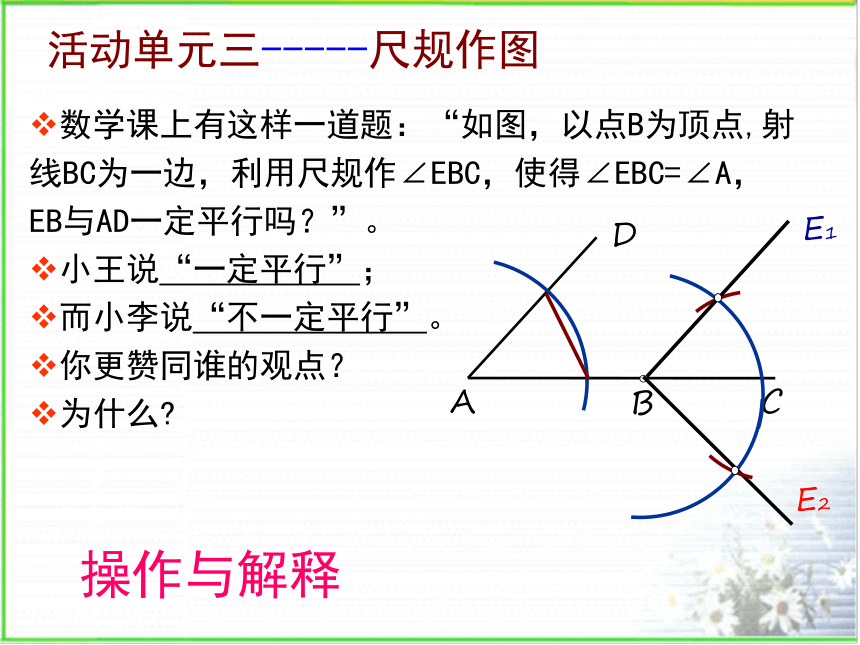
数学课上有这样一道题:“如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A,EB与AD一定平行吗?”。
小王说“一定平行”;
而小李说“不一定平行”。
你更赞同谁的观点?
为什么
A
B
C
D
E1
E2
操作与解释
活动单元三-----尺规作图
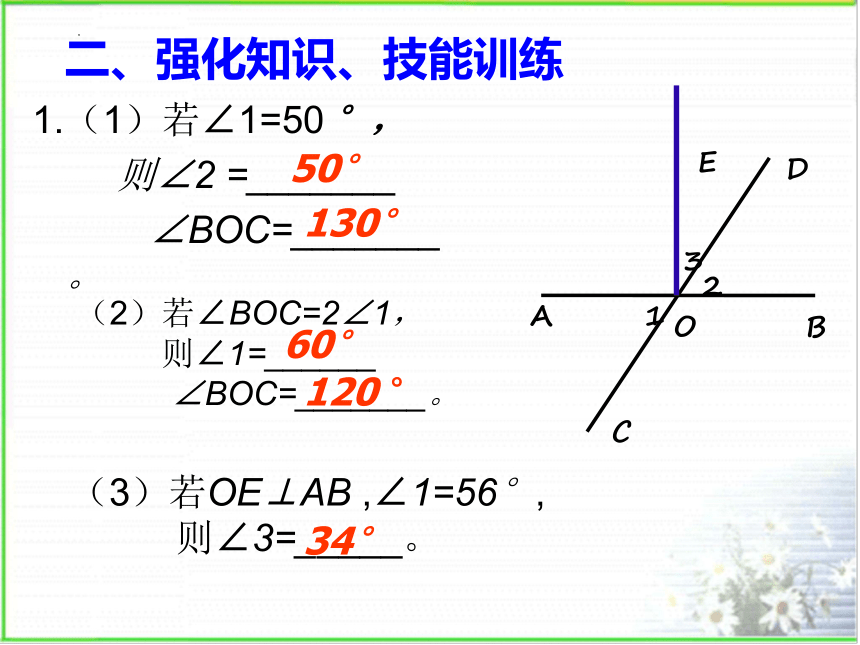
二、强化知识、技能训练
1.(1)若∠1=50 °,
则∠2 =_______
∠BOC=_______。
O
A
B
C
D
2
1
(2)若∠BOC=2∠1,
则∠1=______
∠BOC=_______。
(3)若OE⊥AB ,∠1=56°,
则∠3=_____。
60°
120 °
34°
50°
130°
3
E
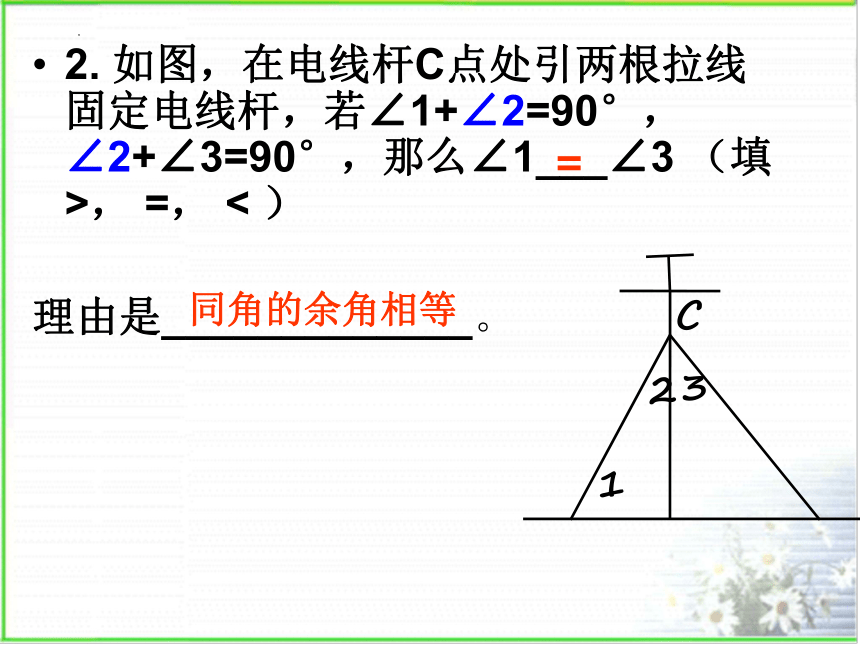
2. 如图,在电线杆C点处引两根拉线固定电线杆,若∠1+∠2=90°,∠2+∠3=90°,那么∠1___∠3 (填 >, =, < )
理由是_____________。
2
1
3
C
=
同角的余角相等
2.如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。(尝试用自己的方式书写说理过程)
A
D
B
C
115°
110°
解:∵AD∥BC ,∠A=115°, ∠D=110°
(已知)
∴∠A+ ∠B=180 °
∠D+ ∠C=180 °
(两直线平行,同旁内角互补)
∴∠B=180°﹣115°=65 °
∠C=180°-110°=70 °
3.图中如果AC∥BD 、AE ∥BF ,那么∠A与∠B的关系如何?你是
怎样思考的?
解:∵AC//BD,AE//BF(已知)
∴∠A=∠DOE
∠B=∠DOE
(两直线平行,同位角相等)
∴∠A=∠B(等量代换)
4.已知,如图直线AB、CD被直线EF所截,且∠1+∠2=180°
求证:AB//CD
A
B
C
D
E
F
1
2
H
G
证明:
解一:∵∠1+∠EHB=180°
(平角的定义)
∠1+∠2=180°(已知)
∴ ∠EHB=∠2
(同角的补角相等)
∴AB//CD
(同位角相等,两直线平行)
解二:∵∠1+∠AHG=180°
(平角的定义)
∠1+∠2=180°(已知)
∴ ∠AHG=∠2
(同角的补角相等)
∴AB//CD
(内错角相等,两直线平行)
解三:∵∠1=∠BHG(对顶角相等)
∠1+∠2=180°(已知)
∴ ∠BHG+∠2=180°
(等量代换)
∴AB//CD
(同旁内角互补,两直线平行)
证明:∵BD平分∠ABC(已知)
∴∠2=∠3(角平分线定义)
又∵∠2=∠1(已知)
∴∠3= ∠1(等量代换)
∴AD∥BC
(内错角相等,两直线平行)
5.如图,已知:∠1=∠2,BD平分∠ABC,试说明AD∥BC.
A
B
C
D
1
2
3
6.如图已知∠1=∠ACB, ∠2=∠3.
求证:CD∥FH.
(小明写了相关的过程,但是却忘了写理由
请你帮他把理由补充完整)
解:∵ ∠1=∠ACB(已知)
∴DE∥BC( )
∴ ∠2 =∠DCF( )
又∵ ∠2=∠3(已知)
∴ ∠3 =∠DCF( )
∴ CD∥FH( )
H
A
C
B
F
D
E
1
2
3
同位角相等,两直线平行
两直线平行,内错角相等
等量代换
同位角相等,两直线平行
7.如图已知AD∥BC,且DC⊥AD于D.
(1)DC与BC有怎样的位置关系?说说你的理由。
(2)你能说明∠1+∠2=180°吗?
A
D
C
B
1
2
4
3
解:(1)∵ DC⊥AD于D(已知)
∴∠3=90°(垂直定义)
又∵ AD∥BC(已知)
∴∠3+∠DCB=180°
(两直线平行,同旁内角互补)
∴ ∠DCB=180°-90°=90°
因此 , DC⊥BC
A
D
C
B
1
2
4
3
(2)
解:∵AD//BC(已知)
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
又∵∠1=∠4(对顶角相等)
∴∠1+∠2=180°(等量代换)
情况1
E在AB与CD之间且向内凹
∠AEC =∠A+∠C
A
B
C
D
E
已知AB∥CD,E为平面内一点(E不在AB和CD上),连接AE,CE,探索∠AEC与∠A,∠C之间的关系。
F
经典题型
解题思路:
过点E作AB的平行线
1
2
3
4
情况2
E在AB与CD之间且向外凸
∠AEC+∠A+∠C=3600
A
B
C
D
E
已知AB∥CD,E为平面内一点(E不在AB和CD上),连接AE,CE,探索∠AEC与∠A,∠C之间的关系。
F
8.如图,已知AB//CD
(1)你能找到∠B、∠D和∠BED的关系吗?
(2)如果∠B=46,∠D=58,则∠E的度数是多少?
A
B
C
D
E
南方新课堂
2、如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC B.∠AFE=∠ACD C.∠3=∠4 D.∠1=∠2
3、如图,AB∥CD,下列结论中错误的是( )
A.∠1=∠2
B.∠2+∠5=180°
C.∠2=∠3
D.∠3+∠4=180°
4、如图,AB∥CD,∠1=128°,FG平分∠EFD,
则∠2的度数是( )
A、46°
B、23°
C、26°
D、24°
128°
条件:1、∠ABC=40°,∠ACB=60°
2、BO,CO分别平分∠ABC和∠ACB
11、如图,已知AB∥DE,∠B=50°,CM平分∠BCE,
CN⊥CM,那么∠DCN=( )度。
12. 已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有( )个.
A.2
B.3
C.4
D.5
A
B
C
D
E
F
O
D
13. 夹在平行线间的两条线段相等,则两条线段所在的直线的位置关系是( )
A 平行 B 相交
C 平行或相交 D不能确定
C
D
14. 在下列给出的条件中,不能判定AB∥DF的是 ( )
A.∠A+∠2=180° B. ∠A=∠3
C. ∠1=∠4 D. ∠1=∠A
15.如图,一束光线AD经CD镜面反射至
镜面AB,再经AB镜面反射至镜面CD,再经
CD镜面反射至镜面AB.已知CD||AB.
(1)从图中找出互相平行的直线,并说明
理由;
A
B
C
D
E
1
2
3
4
5
7
6
(2)若∠A=70 ,求四边形ABCD各个内角
的度数。
16.如图,两平面镜所成的角为∠1,一束光线由点P发出,经OB,OA两次反后,∠1=120°∠PQB=40°
变式
O
A
B
Q
P
R
1
C
(1)PQ与RC平行吗?
(2)要使 PQ与RC平行
必须改变∠1和∠PQB任何一个角的度数,问要改变哪一个角?这个角改变后度数是多少?
17.探究:
下面三个图中,∠ABC的两边分别与∠DEF的两边平行,
即DE∥BA,EF∥BC。
①在图1中,射线BA与射线ED同向,BC与EF也同向;
②在图2中,射线BA与射线ED异向,BC与EF也异向;
③在图3中,射线BA与射线ED同向,BC与EF异向。
问:(1)在上述关系中,∠B与∠E的关系怎样?
(2)你有了怎样的猜想?说出你的认识。
基础闯关
1. 如图,若AO⊥BO, CO⊥DO ,
∠BOC ︰∠AOD =4 ︰5,
则∠BOC = 。
80°
2、如图,想通过码头A向河对岸搭建一座桥,使桥梁最短的搭建方式是沿___搭建,理由是_____若一条船想从码头A开向码头D,则最短路线为___理由是___________.
AC
垂线段最短
AD
两点之间,线段最短
E
D
C
B
A
基础闯关
基础闯关
3、如图,在△ABF中,∠AFB=90°,
FE⊥AB,AF=3,FB=4,AB=5,过点F作
CD∥AB,则点A到直线FB的距离
为__,点A到点B的距离为__,
点F到直线AB的距离为__,直线
CD到直线AB的距离为__ 。
证明: ∵由AC∥DE (已知)
A
D
B
E
1
2
C
∴ ∠ACD= ∠2
(两直线平行,内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD (等量代换)
∴ AB ∥ CD
(内错角相等,两直线平行)
1:如图,已知:AC∥DE,∠1=∠2,
试证明AB∥CD。
能力闯关
∵ EF⊥AB,CD⊥AB
∴ AD∥BC
(垂直于同一条直线的两条直线互相平行)
∴ ∠EFB= ∠DCB
(两直线平行,同位角相等)
∵ ∠EFB=∠GDC
∴ ∠DCB=∠GDC
∴ DG∥BC
(内错角相等,两直线平行)
∴ ∠AGD=∠ACB
(两直线平行,同位角相等)
证明:
2.已知 EF⊥AB,CD⊥AB,
∠EFB=∠GDC,
求证:∠AGD=∠ACB。
能力闯关
3.如图,已知AB ∥ CD, ∠1=∠2,那么∠E与∠F相等吗?试作出判断并说出你的理由。
1
2
3
4
A
B
C
D
E
F
能力闯关
4、如图,已知AB∥CD∥EF,则x、y、z
三者的关系是什么?
能力闯关
5、在如图的方格中,每一个小方格都是边长为1的正方形,点A、B是方格纸中的两个格点,在这个5×5的方格纸中,找出格点C,使△ABC的面积为2个平方单位,则满足条件的格点C的个数是( )个
A. 5 B. 4 C. 3 D. 2
能力闯关
1、如图,∠C+∠A=∠AEC.判断AB与CD
是否平行,并说明理由.
A
C
E
B
D
F
1
挑战自我
2.如图,∠C+∠A=∠AEC.判断AB与CD是否平行,并说明理由.
A
C
E
B
D
1
5
4
3
2
3.如图,∠C+∠A=∠AEC.判断AB与CD
是否平行,并说明理由.
A
C
E
B
D
F
4.如图,∠C+∠A=∠AEC.判断AB与CD
是否平行,并说明理由.
A
C
E
B
D
F
5.如图,已知AB∥CD,∠BAE=135°,
∠AED =80°,∠EDC的度数是( )
F
过点E作EF∥AB
A
B
E
D
C
6.如图,AB∥EF,∠B=105°,
∠DCE =40°,则∠CEF的为( )
F
过点C作EF∥AB
7.如图,AB∥CD,EF⊥AB于点O,FG与CD交于点M,若∠1=43°,则∠2=__________
G
过点F作EG∥AB
1、如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
参考题
方法一:
?
?
O
方法二:
?
?
方法三:
?
?
M
N
方法四:
?
?
O
2、⑴如图a,若AB∥CD,则∠B+∠D=∠E,你能
说明原因?
⑵如图a反之,若∠B+∠D=∠E,直线AB与CD
有什么位置关系?请说明理由。
⑶若将点E移至图b所示位置,此时∠B、∠D、∠E之间有什么关系?请说明理由
⑷若将E点移至图c所示的位置,情况又如何?
⑸在图d中,AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系?
D
B
A
E
C
(a)
A
B
C
D
E
(b)
E
A
B
C
D
(c)
D
A
B
C
E
G
F
(d)
余角和补角的性质
同角或等角的余角相等
同角或等角的补角相等
因为∠1+∠3=90
∠2+∠3=90
所以∠1= ∠2
因为∠1=∠2
∠1+∠3=90
∠2+∠4=90
所以 ∠3= ∠4
相交
一般情况
特殊情况
对顶角相等
邻补角互补
垂直
垂线段最短
点到直线的距离
1
2
3
4
垂线的性质
本章知识结构
两条直线的位置关系
平行
平行公理及推论
平行线的判定和性质
平行线间的距离
第二章 平行线与相交线
复习课
知识点梳理
1、平行线
在同一平面内,不相交的两条直线叫做平行线。
⑴定义:
⑵平行公理 :经过已知直线外一点,有且只有一条直
线与已知直线平行。
⑶平行公理的推论:
如果两条直线都和第三条直线平行,则这两条直线也互相平行。
平行于同一直线的两直线互相平行
概念、性质填空:
一、概念:
两个角的和是_____,称这两个角互为余角。
两个角的和是平角,称这两个角互为_____。
有公共顶点,两边互为反向延长线的两个
角叫做_______。
二、性质:
_________的余角相等;
同角或等角的____相等;
对顶角_____。
直角
补角
对顶角
同角或等角
补角
相等
m
P
O
C
B
A
直线外一点与直线上各点所连的所有线段中垂线段最短
线段PO的长度叫做点P到直线m的距离
三、点到直线的距离
如图:已知∠ACB=90°若
BC=4cm, AC=3cm,AB=5cm, 1.点B到直线AC的距离等于 。
2.点A到直线BC的距离等于 。
3.A、B两点间的距离等于 。
4.你能求出点C到AB的距离吗?你是怎样做的?小组合作交流.
D
因为S△ABC
= 1/2 AB×CD
= 1/2 AC×BC
所以CD=2.4cm
巩固练习
4cm
A
C
B
3cm
5cm
等面积法
三线八角:
两条直线AB与CD被第三条直线EF所截,形成:
(1)同位角:
(2)内错角:
(3)同旁内角:
同位角是 F 形状
内错角是Z形状
同旁内角是U形状
C
A
1
3
7
5
2
8
6
E
4
D
B
F
区别:条件与结论互换,
即:已知平行用特征,探索平行用判定。
3、平行线的判定方法:
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行;
4、平行线的特征:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
a
b
∠1和∠2不是同位角,
同位角的判断
1.如图中的∠1和∠2是同位角吗
1
2
1
2
∠1和∠2是同位角,
数学课上有这样一道题:“如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A,EB与AD一定平行吗?”。
小王说“一定平行”;
而小李说“不一定平行”。
你更赞同谁的观点?
为什么
A
B
C
D
E1
E2
操作与解释
活动单元三-----尺规作图
二、强化知识、技能训练
1.(1)若∠1=50 °,
则∠2 =_______
∠BOC=_______。
O
A
B
C
D
2
1
(2)若∠BOC=2∠1,
则∠1=______
∠BOC=_______。
(3)若OE⊥AB ,∠1=56°,
则∠3=_____。
60°
120 °
34°
50°
130°
3
E
2. 如图,在电线杆C点处引两根拉线固定电线杆,若∠1+∠2=90°,∠2+∠3=90°,那么∠1___∠3 (填 >, =, < )
理由是_____________。
2
1
3
C
=
同角的余角相等
2.如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。(尝试用自己的方式书写说理过程)
A
D
B
C
115°
110°
解:∵AD∥BC ,∠A=115°, ∠D=110°
(已知)
∴∠A+ ∠B=180 °
∠D+ ∠C=180 °
(两直线平行,同旁内角互补)
∴∠B=180°﹣115°=65 °
∠C=180°-110°=70 °
3.图中如果AC∥BD 、AE ∥BF ,那么∠A与∠B的关系如何?你是
怎样思考的?
解:∵AC//BD,AE//BF(已知)
∴∠A=∠DOE
∠B=∠DOE
(两直线平行,同位角相等)
∴∠A=∠B(等量代换)
4.已知,如图直线AB、CD被直线EF所截,且∠1+∠2=180°
求证:AB//CD
A
B
C
D
E
F
1
2
H
G
证明:
解一:∵∠1+∠EHB=180°
(平角的定义)
∠1+∠2=180°(已知)
∴ ∠EHB=∠2
(同角的补角相等)
∴AB//CD
(同位角相等,两直线平行)
解二:∵∠1+∠AHG=180°
(平角的定义)
∠1+∠2=180°(已知)
∴ ∠AHG=∠2
(同角的补角相等)
∴AB//CD
(内错角相等,两直线平行)
解三:∵∠1=∠BHG(对顶角相等)
∠1+∠2=180°(已知)
∴ ∠BHG+∠2=180°
(等量代换)
∴AB//CD
(同旁内角互补,两直线平行)
证明:∵BD平分∠ABC(已知)
∴∠2=∠3(角平分线定义)
又∵∠2=∠1(已知)
∴∠3= ∠1(等量代换)
∴AD∥BC
(内错角相等,两直线平行)
5.如图,已知:∠1=∠2,BD平分∠ABC,试说明AD∥BC.
A
B
C
D
1
2
3
6.如图已知∠1=∠ACB, ∠2=∠3.
求证:CD∥FH.
(小明写了相关的过程,但是却忘了写理由
请你帮他把理由补充完整)
解:∵ ∠1=∠ACB(已知)
∴DE∥BC( )
∴ ∠2 =∠DCF( )
又∵ ∠2=∠3(已知)
∴ ∠3 =∠DCF( )
∴ CD∥FH( )
H
A
C
B
F
D
E
1
2
3
同位角相等,两直线平行
两直线平行,内错角相等
等量代换
同位角相等,两直线平行
7.如图已知AD∥BC,且DC⊥AD于D.
(1)DC与BC有怎样的位置关系?说说你的理由。
(2)你能说明∠1+∠2=180°吗?
A
D
C
B
1
2
4
3
解:(1)∵ DC⊥AD于D(已知)
∴∠3=90°(垂直定义)
又∵ AD∥BC(已知)
∴∠3+∠DCB=180°
(两直线平行,同旁内角互补)
∴ ∠DCB=180°-90°=90°
因此 , DC⊥BC
A
D
C
B
1
2
4
3
(2)
解:∵AD//BC(已知)
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
又∵∠1=∠4(对顶角相等)
∴∠1+∠2=180°(等量代换)
情况1
E在AB与CD之间且向内凹
∠AEC =∠A+∠C
A
B
C
D
E
已知AB∥CD,E为平面内一点(E不在AB和CD上),连接AE,CE,探索∠AEC与∠A,∠C之间的关系。
F
经典题型
解题思路:
过点E作AB的平行线
1
2
3
4
情况2
E在AB与CD之间且向外凸
∠AEC+∠A+∠C=3600
A
B
C
D
E
已知AB∥CD,E为平面内一点(E不在AB和CD上),连接AE,CE,探索∠AEC与∠A,∠C之间的关系。
F
8.如图,已知AB//CD
(1)你能找到∠B、∠D和∠BED的关系吗?
(2)如果∠B=46,∠D=58,则∠E的度数是多少?
A
B
C
D
E
南方新课堂
2、如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC B.∠AFE=∠ACD C.∠3=∠4 D.∠1=∠2
3、如图,AB∥CD,下列结论中错误的是( )
A.∠1=∠2
B.∠2+∠5=180°
C.∠2=∠3
D.∠3+∠4=180°
4、如图,AB∥CD,∠1=128°,FG平分∠EFD,
则∠2的度数是( )
A、46°
B、23°
C、26°
D、24°
128°
条件:1、∠ABC=40°,∠ACB=60°
2、BO,CO分别平分∠ABC和∠ACB
11、如图,已知AB∥DE,∠B=50°,CM平分∠BCE,
CN⊥CM,那么∠DCN=( )度。
12. 已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有( )个.
A.2
B.3
C.4
D.5
A
B
C
D
E
F
O
D
13. 夹在平行线间的两条线段相等,则两条线段所在的直线的位置关系是( )
A 平行 B 相交
C 平行或相交 D不能确定
C
D
14. 在下列给出的条件中,不能判定AB∥DF的是 ( )
A.∠A+∠2=180° B. ∠A=∠3
C. ∠1=∠4 D. ∠1=∠A
15.如图,一束光线AD经CD镜面反射至
镜面AB,再经AB镜面反射至镜面CD,再经
CD镜面反射至镜面AB.已知CD||AB.
(1)从图中找出互相平行的直线,并说明
理由;
A
B
C
D
E
1
2
3
4
5
7
6
(2)若∠A=70 ,求四边形ABCD各个内角
的度数。
16.如图,两平面镜所成的角为∠1,一束光线由点P发出,经OB,OA两次反后,∠1=120°∠PQB=40°
变式
O
A
B
Q
P
R
1
C
(1)PQ与RC平行吗?
(2)要使 PQ与RC平行
必须改变∠1和∠PQB任何一个角的度数,问要改变哪一个角?这个角改变后度数是多少?
17.探究:
下面三个图中,∠ABC的两边分别与∠DEF的两边平行,
即DE∥BA,EF∥BC。
①在图1中,射线BA与射线ED同向,BC与EF也同向;
②在图2中,射线BA与射线ED异向,BC与EF也异向;
③在图3中,射线BA与射线ED同向,BC与EF异向。
问:(1)在上述关系中,∠B与∠E的关系怎样?
(2)你有了怎样的猜想?说出你的认识。
基础闯关
1. 如图,若AO⊥BO, CO⊥DO ,
∠BOC ︰∠AOD =4 ︰5,
则∠BOC = 。
80°
2、如图,想通过码头A向河对岸搭建一座桥,使桥梁最短的搭建方式是沿___搭建,理由是_____若一条船想从码头A开向码头D,则最短路线为___理由是___________.
AC
垂线段最短
AD
两点之间,线段最短
E
D
C
B
A
基础闯关
基础闯关
3、如图,在△ABF中,∠AFB=90°,
FE⊥AB,AF=3,FB=4,AB=5,过点F作
CD∥AB,则点A到直线FB的距离
为__,点A到点B的距离为__,
点F到直线AB的距离为__,直线
CD到直线AB的距离为__ 。
证明: ∵由AC∥DE (已知)
A
D
B
E
1
2
C
∴ ∠ACD= ∠2
(两直线平行,内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD (等量代换)
∴ AB ∥ CD
(内错角相等,两直线平行)
1:如图,已知:AC∥DE,∠1=∠2,
试证明AB∥CD。
能力闯关
∵ EF⊥AB,CD⊥AB
∴ AD∥BC
(垂直于同一条直线的两条直线互相平行)
∴ ∠EFB= ∠DCB
(两直线平行,同位角相等)
∵ ∠EFB=∠GDC
∴ ∠DCB=∠GDC
∴ DG∥BC
(内错角相等,两直线平行)
∴ ∠AGD=∠ACB
(两直线平行,同位角相等)
证明:
2.已知 EF⊥AB,CD⊥AB,
∠EFB=∠GDC,
求证:∠AGD=∠ACB。
能力闯关
3.如图,已知AB ∥ CD, ∠1=∠2,那么∠E与∠F相等吗?试作出判断并说出你的理由。
1
2
3
4
A
B
C
D
E
F
能力闯关
4、如图,已知AB∥CD∥EF,则x、y、z
三者的关系是什么?
能力闯关
5、在如图的方格中,每一个小方格都是边长为1的正方形,点A、B是方格纸中的两个格点,在这个5×5的方格纸中,找出格点C,使△ABC的面积为2个平方单位,则满足条件的格点C的个数是( )个
A. 5 B. 4 C. 3 D. 2
能力闯关
1、如图,∠C+∠A=∠AEC.判断AB与CD
是否平行,并说明理由.
A
C
E
B
D
F
1
挑战自我
2.如图,∠C+∠A=∠AEC.判断AB与CD是否平行,并说明理由.
A
C
E
B
D
1
5
4
3
2
3.如图,∠C+∠A=∠AEC.判断AB与CD
是否平行,并说明理由.
A
C
E
B
D
F
4.如图,∠C+∠A=∠AEC.判断AB与CD
是否平行,并说明理由.
A
C
E
B
D
F
5.如图,已知AB∥CD,∠BAE=135°,
∠AED =80°,∠EDC的度数是( )
F
过点E作EF∥AB
A
B
E
D
C
6.如图,AB∥EF,∠B=105°,
∠DCE =40°,则∠CEF的为( )
F
过点C作EF∥AB
7.如图,AB∥CD,EF⊥AB于点O,FG与CD交于点M,若∠1=43°,则∠2=__________
G
过点F作EG∥AB
1、如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
参考题
方法一:
?
?
O
方法二:
?
?
方法三:
?
?
M
N
方法四:
?
?
O
2、⑴如图a,若AB∥CD,则∠B+∠D=∠E,你能
说明原因?
⑵如图a反之,若∠B+∠D=∠E,直线AB与CD
有什么位置关系?请说明理由。
⑶若将点E移至图b所示位置,此时∠B、∠D、∠E之间有什么关系?请说明理由
⑷若将E点移至图c所示的位置,情况又如何?
⑸在图d中,AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系?
D
B
A
E
C
(a)
A
B
C
D
E
(b)
E
A
B
C
D
(c)
D
A
B
C
E
G
F
(d)
余角和补角的性质
同角或等角的余角相等
同角或等角的补角相等
因为∠1+∠3=90
∠2+∠3=90
所以∠1= ∠2
因为∠1=∠2
∠1+∠3=90
∠2+∠4=90
所以 ∠3= ∠4
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
