华东师大版八年级下册数学 综合与实践 图形的等分 教案
文档属性
| 名称 | 华东师大版八年级下册数学 综合与实践 图形的等分 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 97.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 06:55:50 | ||
图片预览

文档简介
图形的等分教学设计
一、教学目标
知识与技能:经历从特殊到一般的数学过程,不仅掌握中心对称的性质,而且会进行知识迁移,体会割补法,能够推广到任意四边形面积的等分,解决实际问题。
过程与方法:经历观察、猜想、验证等数学活动,发展合情的推理能力和分析问题的能力,较清晰的阐述自己的观点。综合运用所学知识来解决问题,发展应用意识、实践能力与创新能力。
情感态度与价值观:乐于接触社会环境中的数学信息,愿意谈论实践中的数学话题,敢于面对数学活动中的困难,明确理论与实践的差异性,学会辩证分析问题,有独立克服困难和学好数学的自信心。
二、教学的重点和难点
重点:矩形面积的等分,总结对称图形面积的二等分、四等分。
难点:组合图形面积的等分,并把面积两等分运用到现实生活中的解题。
教学方法
主要采取引导启发的教学方法,并在教学中渗透自主探究法、小组讨论法等。
教学过程
情境导入,引入问题
在日常生活中,我们常常会遇到平分问题。比如:你和你的朋友蛋蛋一起去吃披萨,披萨我们都知道,是那种圆圆的薄饼,所以我们可以抽象的将它看成一个平面图形——圆形。现在要把披萨平均分给你和蛋蛋两个人,就是要把这个圆形的面积二等分。
问1:我们应该如何去分割?
问2:这样的直线有多少条?
结论:过圆心的任意一条直线都可以将这个圆形分成面积相等的两部分。
问3:如果要将这个披萨平均分给4个人,应该如何分割?最少切几刀?
【设计意图】结合实际,走出课本,使学生具有强烈的好奇心和求知欲,明白数学来源于生活。
独立尝试,探究问题
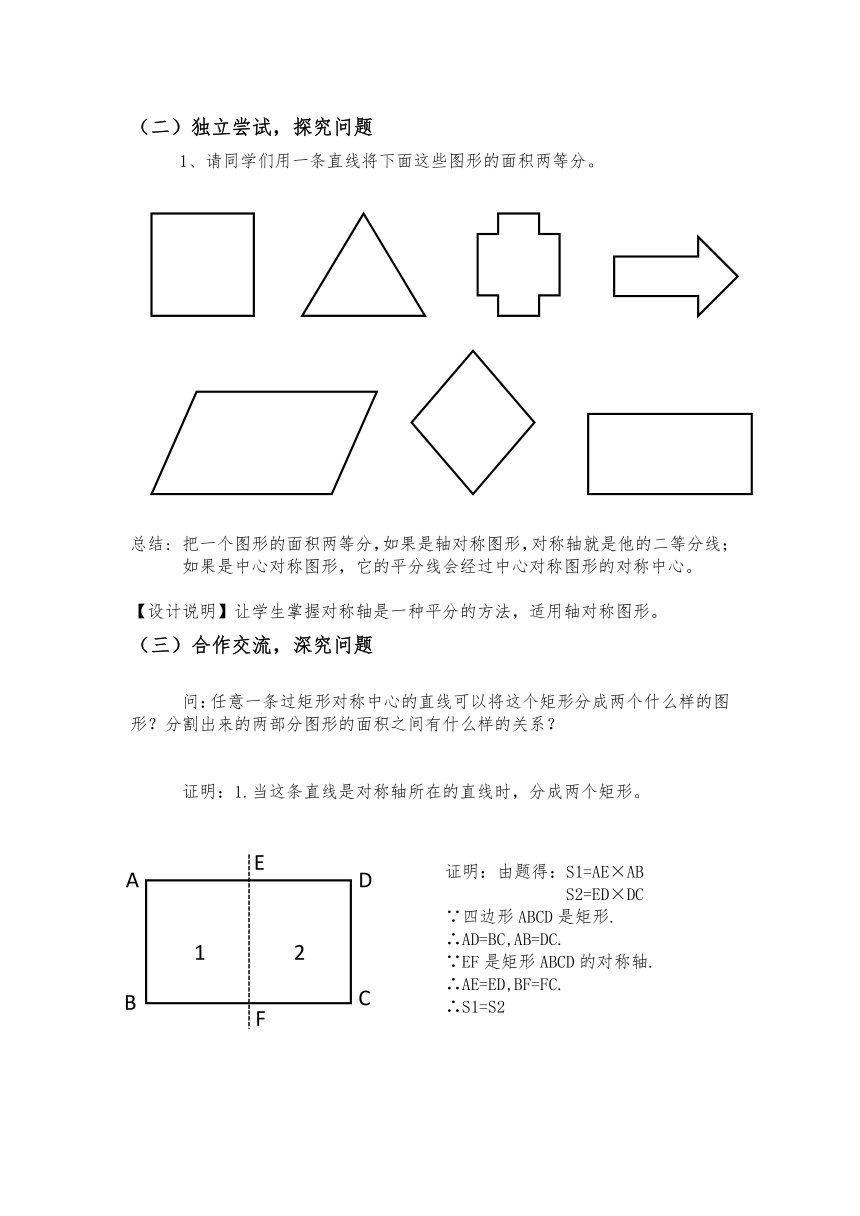
请同学们用一条直线将下面这些图形的面积两等分。
总结: 把一个图形的面积两等分,如果是轴对称图形,对称轴就是他的二等分线;如果是中心对称图形,它的平分线会经过中心对称图形的对称中心。
【设计说明】让学生掌握对称轴是一种平分的方法,适用轴对称图形。
合作交流,深究问题
问:任意一条过矩形对称中心的直线可以将这个矩形分成两个什么样的图形?分割出来的两部分图形的面积之间有什么样的关系?
证明:1.当这条直线是对称轴所在的直线时,分成两个矩形。
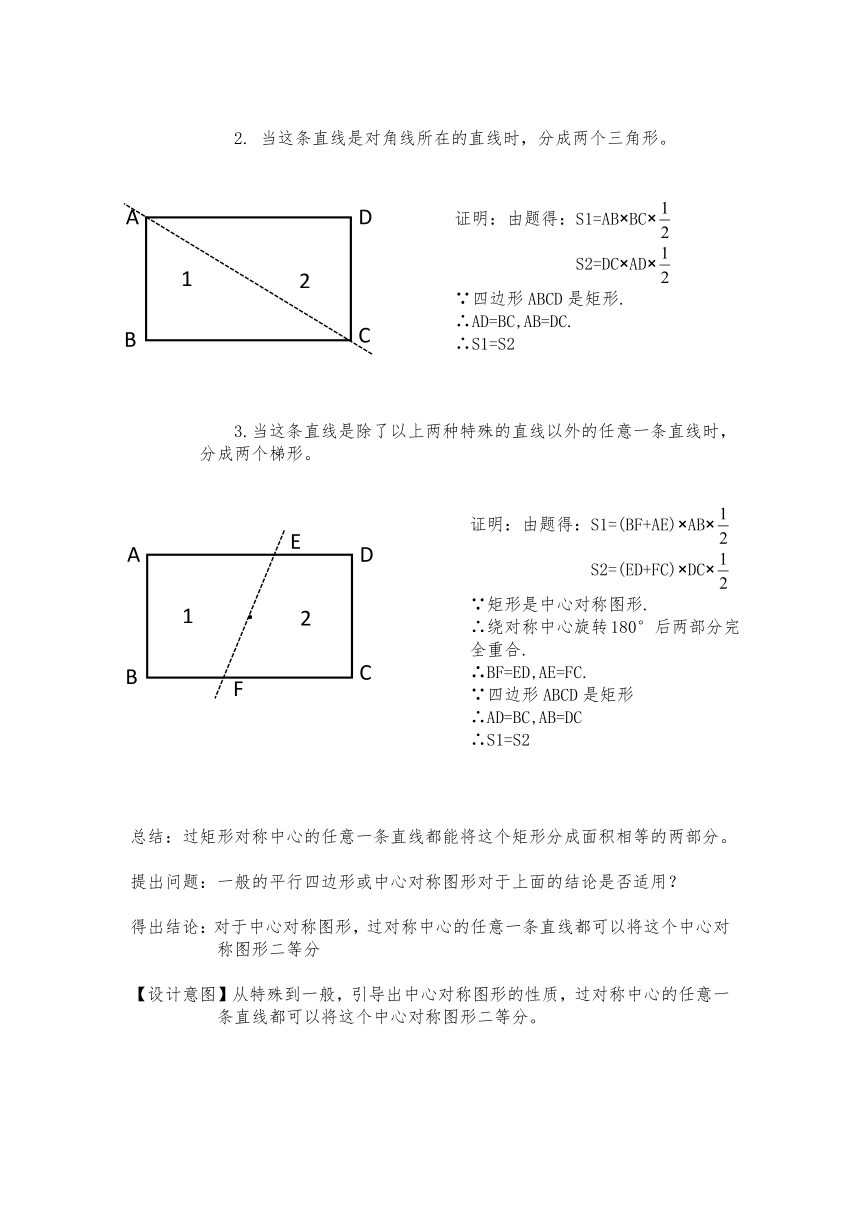
2. 当这条直线是对角线所在的直线时,分成两个三角形。
3.当这条直线是除了以上两种特殊的直线以外的任意一条直线时,分成两个梯形。
总结:过矩形对称中心的任意一条直线都能将这个矩形分成面积相等的两部分。
提出问题:一般的平行四边形或中心对称图形对于上面的结论是否适用?
得出结论:对于中心对称图形,过对称中心的任意一条直线都可以将这个中心对称图形二等分
【设计意图】从特殊到一般,引导出中心对称图形的性质,过对称中心的任意一条直线都可以将这个中心对称图形二等分。
巩固练习
1 .如图,有一“L”形钢板,工人师傅想一刀切成面积相等的两部分,你能帮助工人师傅设计一下吗?
2.在两个平行四边形的内部分别有一个圆和一个矩形。请你各用一条直线分别把左、右两图中的阴影部分分割为面积相等的两部分。
【设计意图】综合运用所学知识来解决问题,检查学生是否掌握把一个图形面积等分。
整合问题
问题:如果要将这个披萨平均分给4个人,应该如何分割?最少切几刀?
总结:先把图形两等分,再把分后得到的图形两等分,是我们的做题思路。对称中心这个特殊的点可以给我们分的时候带来方便。
【设计说明】中心对称图形的对称中心可以给我们作的平分线提供一个点。
拓展探究
如图:下面两图中的正方形分别内接与同一个等腰直角三角形(内接指四个顶点全在三角形的边上),已知左图中正方形面积为72平方厘米,求右图中正方形的面积?
【设计说明】让学生掌握对称轴是一种平分的方法,适用轴对称图形。
课后作业
如图:在正方形ABCD中,画有甲、乙、丙三个小正方形。问:乙、丙面积之和与甲相比,哪一个大些?
板书设计
图形的等分
一、轴对称图形:(1)、(2)、(3)、(4)、(6)、(7)
中心对称图形:(1)、(5)、(6)、(7)
证明:1.当这条直线是对称轴所在的直线时,分成两个矩形。
由题得:S1=AE×AB
S2=ED×DC
∵四边形ABCD是矩形.
∴AD=BC,AB=DC.
∵EF是矩形ABCD的对称轴.
∴AE=ED,BF=FC.
∴S1=S2
当这条直线是对角线所在的直线时,分成两个三角形。
由题得:S1=AB×BC×
S2=DC×AD×
∵四边形ABCD是矩形.
∴AD=BC,AB=DC.
∴S1=S2
当这条直线是除了以上两种特殊的直线以外的任意一条直线时,分成两个梯形。
由题得:S1=(BF+AE)×AB×
S2=(ED+FC)×DC×
∵矩形是中心对称图形.
∴绕对称中心旋转180°后两部分完全重合.
∴BF=ED,AE=FC.
∵四边形ABCD是矩形
∴AD=BC,AB=DC
∴S1=S2
一、教学目标
知识与技能:经历从特殊到一般的数学过程,不仅掌握中心对称的性质,而且会进行知识迁移,体会割补法,能够推广到任意四边形面积的等分,解决实际问题。
过程与方法:经历观察、猜想、验证等数学活动,发展合情的推理能力和分析问题的能力,较清晰的阐述自己的观点。综合运用所学知识来解决问题,发展应用意识、实践能力与创新能力。
情感态度与价值观:乐于接触社会环境中的数学信息,愿意谈论实践中的数学话题,敢于面对数学活动中的困难,明确理论与实践的差异性,学会辩证分析问题,有独立克服困难和学好数学的自信心。
二、教学的重点和难点
重点:矩形面积的等分,总结对称图形面积的二等分、四等分。
难点:组合图形面积的等分,并把面积两等分运用到现实生活中的解题。
教学方法
主要采取引导启发的教学方法,并在教学中渗透自主探究法、小组讨论法等。
教学过程
情境导入,引入问题
在日常生活中,我们常常会遇到平分问题。比如:你和你的朋友蛋蛋一起去吃披萨,披萨我们都知道,是那种圆圆的薄饼,所以我们可以抽象的将它看成一个平面图形——圆形。现在要把披萨平均分给你和蛋蛋两个人,就是要把这个圆形的面积二等分。
问1:我们应该如何去分割?
问2:这样的直线有多少条?
结论:过圆心的任意一条直线都可以将这个圆形分成面积相等的两部分。
问3:如果要将这个披萨平均分给4个人,应该如何分割?最少切几刀?
【设计意图】结合实际,走出课本,使学生具有强烈的好奇心和求知欲,明白数学来源于生活。
独立尝试,探究问题
请同学们用一条直线将下面这些图形的面积两等分。
总结: 把一个图形的面积两等分,如果是轴对称图形,对称轴就是他的二等分线;如果是中心对称图形,它的平分线会经过中心对称图形的对称中心。
【设计说明】让学生掌握对称轴是一种平分的方法,适用轴对称图形。
合作交流,深究问题
问:任意一条过矩形对称中心的直线可以将这个矩形分成两个什么样的图形?分割出来的两部分图形的面积之间有什么样的关系?
证明:1.当这条直线是对称轴所在的直线时,分成两个矩形。
2. 当这条直线是对角线所在的直线时,分成两个三角形。
3.当这条直线是除了以上两种特殊的直线以外的任意一条直线时,分成两个梯形。
总结:过矩形对称中心的任意一条直线都能将这个矩形分成面积相等的两部分。
提出问题:一般的平行四边形或中心对称图形对于上面的结论是否适用?
得出结论:对于中心对称图形,过对称中心的任意一条直线都可以将这个中心对称图形二等分
【设计意图】从特殊到一般,引导出中心对称图形的性质,过对称中心的任意一条直线都可以将这个中心对称图形二等分。
巩固练习
1 .如图,有一“L”形钢板,工人师傅想一刀切成面积相等的两部分,你能帮助工人师傅设计一下吗?
2.在两个平行四边形的内部分别有一个圆和一个矩形。请你各用一条直线分别把左、右两图中的阴影部分分割为面积相等的两部分。
【设计意图】综合运用所学知识来解决问题,检查学生是否掌握把一个图形面积等分。
整合问题
问题:如果要将这个披萨平均分给4个人,应该如何分割?最少切几刀?
总结:先把图形两等分,再把分后得到的图形两等分,是我们的做题思路。对称中心这个特殊的点可以给我们分的时候带来方便。
【设计说明】中心对称图形的对称中心可以给我们作的平分线提供一个点。
拓展探究
如图:下面两图中的正方形分别内接与同一个等腰直角三角形(内接指四个顶点全在三角形的边上),已知左图中正方形面积为72平方厘米,求右图中正方形的面积?
【设计说明】让学生掌握对称轴是一种平分的方法,适用轴对称图形。
课后作业
如图:在正方形ABCD中,画有甲、乙、丙三个小正方形。问:乙、丙面积之和与甲相比,哪一个大些?
板书设计
图形的等分
一、轴对称图形:(1)、(2)、(3)、(4)、(6)、(7)
中心对称图形:(1)、(5)、(6)、(7)
证明:1.当这条直线是对称轴所在的直线时,分成两个矩形。
由题得:S1=AE×AB
S2=ED×DC
∵四边形ABCD是矩形.
∴AD=BC,AB=DC.
∵EF是矩形ABCD的对称轴.
∴AE=ED,BF=FC.
∴S1=S2
当这条直线是对角线所在的直线时,分成两个三角形。
由题得:S1=AB×BC×
S2=DC×AD×
∵四边形ABCD是矩形.
∴AD=BC,AB=DC.
∴S1=S2
当这条直线是除了以上两种特殊的直线以外的任意一条直线时,分成两个梯形。
由题得:S1=(BF+AE)×AB×
S2=(ED+FC)×DC×
∵矩形是中心对称图形.
∴绕对称中心旋转180°后两部分完全重合.
∴BF=ED,AE=FC.
∵四边形ABCD是矩形
∴AD=BC,AB=DC
∴S1=S2
