人教版数学八年级下册第19章 一次函数 复习课件(45张PPT)
文档属性
| 名称 | 人教版数学八年级下册第19章 一次函数 复习课件(45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 06:56:57 | ||
图片预览









文档简介
(共45张PPT)
《一次函数》复习课件
考点梳理
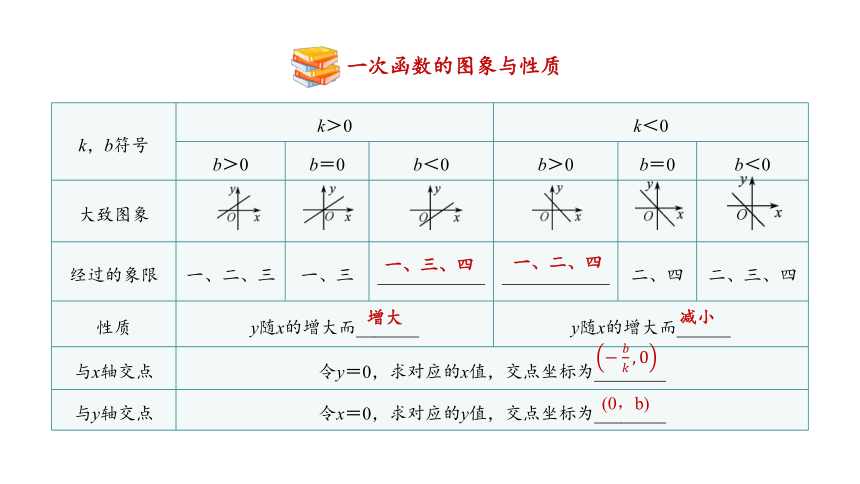
考点1 一次函数的图象与性质
定义、图象及性质
1.一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.
2.当b=____时,y=kx(k≠0)为正比例函数,正比例函数是一种特殊的一次函数.
一次函数与正比例函数
0
k,b符号 k>0 k<0 b>0 b=0 b<0 b>0 b=0 b<0
大致图象
经过的象限 一、二、三 一、三 ____________ ____________ 二、四 二、三、四
性质 y随x的增大而_______ y随x的增大而______ 与x轴交点 令y=0,求对应的x值,交点坐标为________ 与y轴交点 令x=0,求对应的y值,交点坐标为________ 一次函数的图象与性质
一、三、四
一、二、四
增大
减小
(0,b)
同一平面直角坐标系中两直线(l1:y1=k1x+b1, l2:y2=k2x+b2)
考点专练
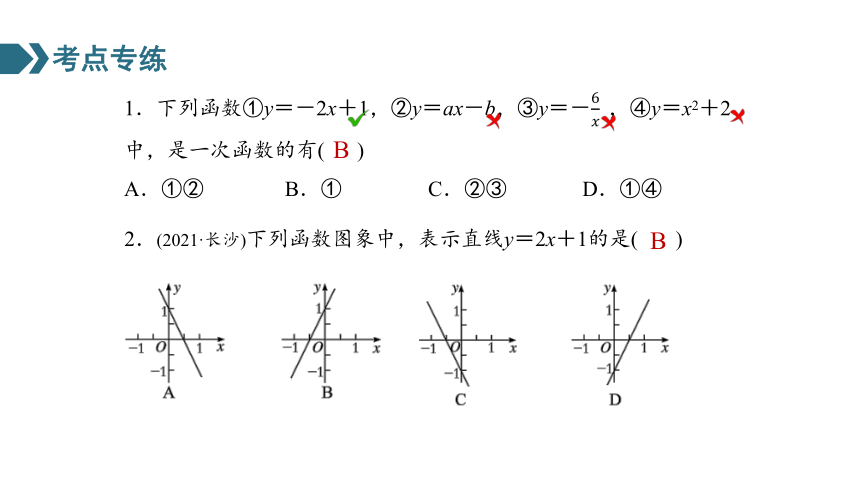
1.下列函数①y=-2x+1,②y=ax-b,③y=-,④y=x2+2中,是一次函数的有( )
A.①② B.① C.②③ D.①④
B
2.(2021·长沙)下列函数图象中,表示直线y=2x+1的是( )
B
3.直线y=x+1与y=-2x+a的交点在第一象限,则a的取值可以是( )
A.-1 B.0 C.1 D.2
D
y=x+1
y=-2x+a
x=
y=
>0
>0
a>1
4.(2021·营口)已知一次函数y=kx-k过点(-1,4),则下列结论正确的是( )
A.y随x增大而增大
B.k=2
C.直线过点(1,0)
D.与坐标轴围成的三角形面积为2
4=(-1)k-k
k =-2
y=-2x+2
当x=1, y=0
x
y
O
1
2
三角形面积S= ×1×2=1
C
5.(2021·上海)已知函数y=kx经过二、四象限,且函数不经过(-1,1),请写出一个符合条件的函数解析式____________.
y=-2x
k<0
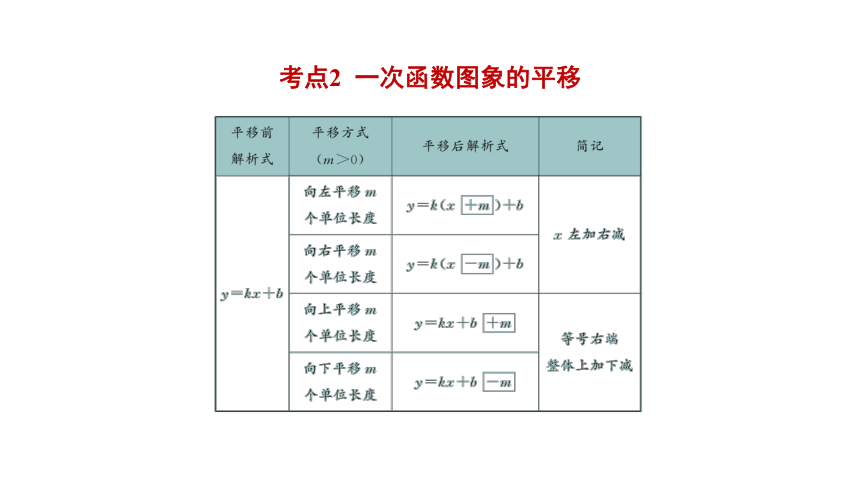
考点2 一次函数图象的平移
6.(2021·黄石)将直线y=-x+1向左平移m(m>0)个单位后,经过点(1,-3),则m的值为______.
考点专练
y=-(x+m)+1
-3=-(1+m)+1
m =3
3
考点3 一次函数解析式的确定
此考点是必考点,是函数中至关重要的考点,是解决一次函数问题的基础与关键点.
考情分析
待定系数法求一次函数解析式的步骤
考点专练
7.(2021·江西南昌一模)已知一次函数y=kx+b(k≠0)经过(1,-2),(-2,3)两点,则它的图象不经过第______象限.
x
y
O
(1,-2)
(-2,3)
一
8.(2021·广西桂林)如图,与图中直线y=-x+1关于x轴对称的直线的函数解析式是 ____________.
y=x-1
-1
考点4 一次函数与一次方程(组)、不等式的关系
一次函数与方程(组)的关系
一次函数与方程(组)的关系 一次函数y=kx+b的解析式可以看成是一个二元一次方程
一次函数y=kx+b的图象与x轴的交点的横坐标是关于x的方程___________的根
一次函数y=k1x+b1与一次函数y=k2x+b2的图象的交点坐标就是方程组
________________的解
kx+b=0
一次函数与不等式的关系
一次函数与不等式的关系 直线y=kx+b在x轴上方的点的横坐标就是不等式______________ 的解集
直线y=kx+b在x轴下方的点的横坐标就是不等式______________ 的解集
直线l1:y1=k1x+b1,l2:y2=k2x+b2的图象在平面直角坐标系的位置与函数值之间的关系:当直线l1在直线l2上方时,y1>y2;当直线l1在直线l2下方时,y1kx+b>0
kx+b<0
遇到一次函数与不等式问题,要注意利用数形结合思想,先画出对应的函数图象,再结合图象及不等号方向确定对应的自变量x的取值范围.正确读图,从图象中提取信息是解决此类问题的关键.
方法点拨
9.(2020·济宁)数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
考点专练
A
10.(2021·贺州)直线y=ax+b(a≠0)过点A(0,1),B(2,0),则关于x的方程ax+b=0的解为( )
A.x=0 B.x=1 C.x=2 D.x=3
y=ax+b
ax+b=0
B(2,0)
C
11.(2021·娄底)如图,直线y=x+b和y=kx+4与x轴分别相交于点A(-4,0),点B(2,0),则的解集为( )
A.-4<x<2 B.x<-4
C.x>2 D.x<-4或x>2
A
考点5 一次函数的实际应用
利用一次函数解决实际问题,首先建立函数模型,然后求出函数解析式,最后根据函数解析式、函数性质作答.
由实际问题得到的一次函数解析式,自变量的取值范围一般受到限制,则图象为线段或射线,根据函数的性质,存在最大值或最小值问题
易错提醒
1.(2021·济南)漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位h(cm)是时间t(min)的一次函数,下表是小明记录的部分数据,其中有一个h的值记录错误,请排除后利用正确的数据确定当h为8 cm时,对应的时间t为________min.
t(min) … 1 2 3 5 …
h(cm) … 2.4 2.8 3.4 4 …
15
考点专练
2.(2020·青岛)为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480 m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自注水速度保持不变,同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示.
(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;
(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍,求单独打开甲进水口注满游泳池需多少小时?
解:(1)函数关系式为y=140t+100,
同时打开甲、乙两个进水口的注水速度为140 m3/h.
(2)单独打开甲进水口注满游泳池需8 h.
典例讲析
题型一 一次函数的图象与性质
例1. (2021·江西模拟)如图,在平面直角坐标系中,已知四边形OABC是矩形,OA=1,AB=2,过点B的直线y=3x+n与y轴交于点D,过点B作直线BE⊥BD交x轴于点E.
(1)求点D的坐标;
(2)求直线BE的解析式.
解:(1)如图,∵OA=1,AB=2,∴B(1,2),
∵直线y=3x+n过点B,
∴3×1+n=2,解得n=-1,
∴直线BD的解析式为:y=3x-1,
∵直线y=3x-1与y轴交于点D,
令x=0,可得y=-1,
∴D(0,-1).
例1. (2021·江西模拟)如图,在平面直角坐标系中,已知四边形OABC是矩形,OA=1,AB=2,过点B的直线y=3x+n与y轴交于点D,过点B作直线BE⊥BD交x轴于点E.
(1)求点D的坐标;
解: (2)设直线BE的解析式为y=kx+b,
∵BE⊥BD,∴k=-,
∵B(1,2),
∴-×1+b=2,解得b= ,
∴直线BE的解析式为y=- x+ .
例1. (2021·江西模拟)如图,在平面直角坐标系中,已知四边形OABC是矩形,OA=1,AB=2,过点B的直线y=3x+n与y轴交于点D,过点B作直线BE⊥BD交x轴于点E.
(2)求直线BE的解析式.
跟踪练习
1.对于一次函数y=x+2,下列说法不正确的是( )
A.图象经过点(1,3)
B.图象与x轴交于点(-2,0)
C.图象不经过第四象限
D.当x>2时,y<4
1+2=3
x
y
O
y=x+2
当x>2时,y>4
D
2.如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=.
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
点B的坐标为(0,3)
2
3
(2)若△ABC的面积为4,求直线l2的解析式.
解: (2)∵△ABC的面积为4,
∴ ×BC×AO=4,
∴ ×BC×2=4,即BC=4,可求得C(0,-1),
设l2的解析式为y=kx+b,
∴l2的解析式为y= x-1.
则解得
题型二 一次函数综合题
例2. (2021·西藏)已知第一象限点P(x,y)在直线y=-x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(1)当点P的横坐标为2时,求△AOP的面积;
(2)当S=4时,求点P的坐标;
(3)求S关于x的函数解析式,写出x的取值范围,并在图中画出函数S的图象.
解:(1)把点P的横坐标代入y=-x+5得,y=-2+5=3,
例2. (2021·西藏)已知第一象限点P(x,y)在直线y=-x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(1)当点P的横坐标为2时,求△AOP的面积;
∴S△AOP= ×4×3=6;
∴点P(2,3),
y=-x+5
P
A
∴点P的坐标为(3,2);
例2. (2021·西藏)已知第一象限点P(x,y)在直线y=-x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(2)当S=4时,求点P的坐标;
y=-x+5
P
A
解: (2)当S=4时,即×4×|y|=4,
∴y=2或y=-2(舍去),
当y=2时,即2=-x+5,解得x=3,
∴点P(3,2),
∴S关于x的函数解析式为S=-2x+10(0<x<5)
例2. (2021·西藏)已知第一象限点P(x,y)在直线y=-x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(3)求S关于x的函数解析式,写出x的取值范围,并在图中画出函数S的图象.
解: (3)由题意得,S= OA·|y|=2|y|,
∵点P在第一象限,
∴y>0,即0<x<5时,S=2(-x+5)=-2x+10,
画出的图象如图所示.
跟踪练习
3.如图,在平面直角坐标系中,点A,B的坐标分别为(-,0),(,1),连接AB,以AB为边向上作等边三角形ABC.
(1)求点C的坐标;
(2)求线段BC所在直线的解析式.
∴点C的坐标为(-,2);
3.如图,在平面直角坐标系中,点A,B的坐标分别为(-,0),(,1),连接AB,以AB为边向上作等边三角形ABC.
(1)求点C的坐标;
解:(1)过点B作BH⊥x轴,点A坐标为(-,0),点B坐标为(,1),
可证∠BAH=30°,
∵△ABC为等边三角形,
∴AB=AC=2,∴∠CAB+∠BAH=90°,
∴点C的纵坐标为2,
H
-
∴直线BC的函数解析式为y=- x+ .
3.如图,在平面直角坐标系中,点A,B的坐标分别为(-,0),(,1),连接AB,以AB为边向上作等边三角形ABC.
(2)求线段BC所在直线的解析式.
解: (2)设直线BC的解析式为:y=kx+b,
则解得
H
-
随堂练习
1.已知正比例函数y=kx(k≠0)的图象过点(2,3),把正比例函数y=kx(k≠0)的图象平移,使它过点(1,-1),则平移后的函数图象大致是( )
y= x
y= x+k
-1= +k
k=-
y= x-
D
2.(2021·抚顺)如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x= B.x=1 C.x=2 D.x=4
m的值
点P(m,2)代入直线y=2x得
2m=2
∴m=1
B
3.(2021·嘉兴)已知点P(a,b)在直线y=-3x-4上,且2a-5b≤0,则下列不等式一定成立的是( )
A. ≤ B. ≥ C. ≥ D. ≤
b=-3a-4
2a-5(-3a-4)≤0
2a +15a +20≤0
17a +20≤0
a ≤
<0
b ≥
2a-5b≤0
2a ≤ 5b
2 ≥ 5
≤
D
4.(2021·眉山)一次函数y=(2a+3)x+2的值随x值的增大而减少,则常数a的取值范围是_____________.
2a+3<0
a<
a<
5.(2021·江西南昌模拟)已知直线y=m与一次函数y=mx+m和y=-mx-m的图象分别相交于A,B两点,则AB=_____.
x
y
O
m
(-2,m)
2
2
6.(2021·梧州)如图,在同一平面直角坐标系中,直线l1:y= x+ 与直线l2:y=kx+3相交于点A,则方程组的解为________________.
7.(2021·贺州)如图,一次函数y=x+4与坐标轴分别交于A,B两点,点P,C分别是线段AB,OB上的点,且∠OPC=45°,PC=PO,则点P的坐标为_____________________.
(-2,4-2)
△APO≌ △BCP
4
4
2
4- 4
4-2
中考失分点专练:忽视一次函数图象的性质而漏解
一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,则这个函数的解析式为____________________________________.
y= x-4或y=-x-3
《一次函数》复习课件
考点梳理
考点1 一次函数的图象与性质
定义、图象及性质
1.一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.
2.当b=____时,y=kx(k≠0)为正比例函数,正比例函数是一种特殊的一次函数.
一次函数与正比例函数
0
k,b符号 k>0 k<0 b>0 b=0 b<0 b>0 b=0 b<0
大致图象
经过的象限 一、二、三 一、三 ____________ ____________ 二、四 二、三、四
性质 y随x的增大而_______ y随x的增大而______ 与x轴交点 令y=0,求对应的x值,交点坐标为________ 与y轴交点 令x=0,求对应的y值,交点坐标为________ 一次函数的图象与性质
一、三、四
一、二、四
增大
减小
(0,b)
同一平面直角坐标系中两直线(l1:y1=k1x+b1, l2:y2=k2x+b2)
考点专练
1.下列函数①y=-2x+1,②y=ax-b,③y=-,④y=x2+2中,是一次函数的有( )
A.①② B.① C.②③ D.①④
B
2.(2021·长沙)下列函数图象中,表示直线y=2x+1的是( )
B
3.直线y=x+1与y=-2x+a的交点在第一象限,则a的取值可以是( )
A.-1 B.0 C.1 D.2
D
y=x+1
y=-2x+a
x=
y=
>0
>0
a>1
4.(2021·营口)已知一次函数y=kx-k过点(-1,4),则下列结论正确的是( )
A.y随x增大而增大
B.k=2
C.直线过点(1,0)
D.与坐标轴围成的三角形面积为2
4=(-1)k-k
k =-2
y=-2x+2
当x=1, y=0
x
y
O
1
2
三角形面积S= ×1×2=1
C
5.(2021·上海)已知函数y=kx经过二、四象限,且函数不经过(-1,1),请写出一个符合条件的函数解析式____________.
y=-2x
k<0
考点2 一次函数图象的平移
6.(2021·黄石)将直线y=-x+1向左平移m(m>0)个单位后,经过点(1,-3),则m的值为______.
考点专练
y=-(x+m)+1
-3=-(1+m)+1
m =3
3
考点3 一次函数解析式的确定
此考点是必考点,是函数中至关重要的考点,是解决一次函数问题的基础与关键点.
考情分析
待定系数法求一次函数解析式的步骤
考点专练
7.(2021·江西南昌一模)已知一次函数y=kx+b(k≠0)经过(1,-2),(-2,3)两点,则它的图象不经过第______象限.
x
y
O
(1,-2)
(-2,3)
一
8.(2021·广西桂林)如图,与图中直线y=-x+1关于x轴对称的直线的函数解析式是 ____________.
y=x-1
-1
考点4 一次函数与一次方程(组)、不等式的关系
一次函数与方程(组)的关系
一次函数与方程(组)的关系 一次函数y=kx+b的解析式可以看成是一个二元一次方程
一次函数y=kx+b的图象与x轴的交点的横坐标是关于x的方程___________的根
一次函数y=k1x+b1与一次函数y=k2x+b2的图象的交点坐标就是方程组
________________的解
kx+b=0
一次函数与不等式的关系
一次函数与不等式的关系 直线y=kx+b在x轴上方的点的横坐标就是不等式______________ 的解集
直线y=kx+b在x轴下方的点的横坐标就是不等式______________ 的解集
直线l1:y1=k1x+b1,l2:y2=k2x+b2的图象在平面直角坐标系的位置与函数值之间的关系:当直线l1在直线l2上方时,y1>y2;当直线l1在直线l2下方时,y1
kx+b<0
遇到一次函数与不等式问题,要注意利用数形结合思想,先画出对应的函数图象,再结合图象及不等号方向确定对应的自变量x的取值范围.正确读图,从图象中提取信息是解决此类问题的关键.
方法点拨
9.(2020·济宁)数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
考点专练
A
10.(2021·贺州)直线y=ax+b(a≠0)过点A(0,1),B(2,0),则关于x的方程ax+b=0的解为( )
A.x=0 B.x=1 C.x=2 D.x=3
y=ax+b
ax+b=0
B(2,0)
C
11.(2021·娄底)如图,直线y=x+b和y=kx+4与x轴分别相交于点A(-4,0),点B(2,0),则的解集为( )
A.-4<x<2 B.x<-4
C.x>2 D.x<-4或x>2
A
考点5 一次函数的实际应用
利用一次函数解决实际问题,首先建立函数模型,然后求出函数解析式,最后根据函数解析式、函数性质作答.
由实际问题得到的一次函数解析式,自变量的取值范围一般受到限制,则图象为线段或射线,根据函数的性质,存在最大值或最小值问题
易错提醒
1.(2021·济南)漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位h(cm)是时间t(min)的一次函数,下表是小明记录的部分数据,其中有一个h的值记录错误,请排除后利用正确的数据确定当h为8 cm时,对应的时间t为________min.
t(min) … 1 2 3 5 …
h(cm) … 2.4 2.8 3.4 4 …
15
考点专练
2.(2020·青岛)为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480 m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自注水速度保持不变,同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示.
(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;
(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍,求单独打开甲进水口注满游泳池需多少小时?
解:(1)函数关系式为y=140t+100,
同时打开甲、乙两个进水口的注水速度为140 m3/h.
(2)单独打开甲进水口注满游泳池需8 h.
典例讲析
题型一 一次函数的图象与性质
例1. (2021·江西模拟)如图,在平面直角坐标系中,已知四边形OABC是矩形,OA=1,AB=2,过点B的直线y=3x+n与y轴交于点D,过点B作直线BE⊥BD交x轴于点E.
(1)求点D的坐标;
(2)求直线BE的解析式.
解:(1)如图,∵OA=1,AB=2,∴B(1,2),
∵直线y=3x+n过点B,
∴3×1+n=2,解得n=-1,
∴直线BD的解析式为:y=3x-1,
∵直线y=3x-1与y轴交于点D,
令x=0,可得y=-1,
∴D(0,-1).
例1. (2021·江西模拟)如图,在平面直角坐标系中,已知四边形OABC是矩形,OA=1,AB=2,过点B的直线y=3x+n与y轴交于点D,过点B作直线BE⊥BD交x轴于点E.
(1)求点D的坐标;
解: (2)设直线BE的解析式为y=kx+b,
∵BE⊥BD,∴k=-,
∵B(1,2),
∴-×1+b=2,解得b= ,
∴直线BE的解析式为y=- x+ .
例1. (2021·江西模拟)如图,在平面直角坐标系中,已知四边形OABC是矩形,OA=1,AB=2,过点B的直线y=3x+n与y轴交于点D,过点B作直线BE⊥BD交x轴于点E.
(2)求直线BE的解析式.
跟踪练习
1.对于一次函数y=x+2,下列说法不正确的是( )
A.图象经过点(1,3)
B.图象与x轴交于点(-2,0)
C.图象不经过第四象限
D.当x>2时,y<4
1+2=3
x
y
O
y=x+2
当x>2时,y>4
D
2.如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=.
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
点B的坐标为(0,3)
2
3
(2)若△ABC的面积为4,求直线l2的解析式.
解: (2)∵△ABC的面积为4,
∴ ×BC×AO=4,
∴ ×BC×2=4,即BC=4,可求得C(0,-1),
设l2的解析式为y=kx+b,
∴l2的解析式为y= x-1.
则解得
题型二 一次函数综合题
例2. (2021·西藏)已知第一象限点P(x,y)在直线y=-x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(1)当点P的横坐标为2时,求△AOP的面积;
(2)当S=4时,求点P的坐标;
(3)求S关于x的函数解析式,写出x的取值范围,并在图中画出函数S的图象.
解:(1)把点P的横坐标代入y=-x+5得,y=-2+5=3,
例2. (2021·西藏)已知第一象限点P(x,y)在直线y=-x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(1)当点P的横坐标为2时,求△AOP的面积;
∴S△AOP= ×4×3=6;
∴点P(2,3),
y=-x+5
P
A
∴点P的坐标为(3,2);
例2. (2021·西藏)已知第一象限点P(x,y)在直线y=-x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(2)当S=4时,求点P的坐标;
y=-x+5
P
A
解: (2)当S=4时,即×4×|y|=4,
∴y=2或y=-2(舍去),
当y=2时,即2=-x+5,解得x=3,
∴点P(3,2),
∴S关于x的函数解析式为S=-2x+10(0<x<5)
例2. (2021·西藏)已知第一象限点P(x,y)在直线y=-x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(3)求S关于x的函数解析式,写出x的取值范围,并在图中画出函数S的图象.
解: (3)由题意得,S= OA·|y|=2|y|,
∵点P在第一象限,
∴y>0,即0<x<5时,S=2(-x+5)=-2x+10,
画出的图象如图所示.
跟踪练习
3.如图,在平面直角坐标系中,点A,B的坐标分别为(-,0),(,1),连接AB,以AB为边向上作等边三角形ABC.
(1)求点C的坐标;
(2)求线段BC所在直线的解析式.
∴点C的坐标为(-,2);
3.如图,在平面直角坐标系中,点A,B的坐标分别为(-,0),(,1),连接AB,以AB为边向上作等边三角形ABC.
(1)求点C的坐标;
解:(1)过点B作BH⊥x轴,点A坐标为(-,0),点B坐标为(,1),
可证∠BAH=30°,
∵△ABC为等边三角形,
∴AB=AC=2,∴∠CAB+∠BAH=90°,
∴点C的纵坐标为2,
H
-
∴直线BC的函数解析式为y=- x+ .
3.如图,在平面直角坐标系中,点A,B的坐标分别为(-,0),(,1),连接AB,以AB为边向上作等边三角形ABC.
(2)求线段BC所在直线的解析式.
解: (2)设直线BC的解析式为:y=kx+b,
则解得
H
-
随堂练习
1.已知正比例函数y=kx(k≠0)的图象过点(2,3),把正比例函数y=kx(k≠0)的图象平移,使它过点(1,-1),则平移后的函数图象大致是( )
y= x
y= x+k
-1= +k
k=-
y= x-
D
2.(2021·抚顺)如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x= B.x=1 C.x=2 D.x=4
m的值
点P(m,2)代入直线y=2x得
2m=2
∴m=1
B
3.(2021·嘉兴)已知点P(a,b)在直线y=-3x-4上,且2a-5b≤0,则下列不等式一定成立的是( )
A. ≤ B. ≥ C. ≥ D. ≤
b=-3a-4
2a-5(-3a-4)≤0
2a +15a +20≤0
17a +20≤0
a ≤
<0
b ≥
2a-5b≤0
2a ≤ 5b
2 ≥ 5
≤
D
4.(2021·眉山)一次函数y=(2a+3)x+2的值随x值的增大而减少,则常数a的取值范围是_____________.
2a+3<0
a<
a<
5.(2021·江西南昌模拟)已知直线y=m与一次函数y=mx+m和y=-mx-m的图象分别相交于A,B两点,则AB=_____.
x
y
O
m
(-2,m)
2
2
6.(2021·梧州)如图,在同一平面直角坐标系中,直线l1:y= x+ 与直线l2:y=kx+3相交于点A,则方程组的解为________________.
7.(2021·贺州)如图,一次函数y=x+4与坐标轴分别交于A,B两点,点P,C分别是线段AB,OB上的点,且∠OPC=45°,PC=PO,则点P的坐标为_____________________.
(-2,4-2)
△APO≌ △BCP
4
4
2
4- 4
4-2
中考失分点专练:忽视一次函数图象的性质而漏解
一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,则这个函数的解析式为____________________________________.
y= x-4或y=-x-3
