苏科版七年级数学下册 10.5 用二元一次方程组解决问题 课件(共18张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 10.5 用二元一次方程组解决问题 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 216.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
10.5 用二元一次方程组解决问题
1、会列二元一次方程组解决行程问题。
2、体会列二元一次方程组解决行程问题的一般步骤,将实际问题转化成二元一次方程组的数学模型。
教学目标:
重点、难点:
重点:1、会列二元一次方程组解决行程问题。
2、将实际问题转化成二元一次方程组
的数学模型。
难点:将实际问题转化成二元一次方程组的
数学模型。
(一)课前预习
1、列二元一次方程组解应用题的一般步骤是什么?
审 设 列 解 验 答
实际问题
数学问题
抽象
已知量、未知量,等量关系
二元一次方程组
方程组的解
解的合理性
实际问题答案
分析
列出
求出
验证
合理
设未知数
2、与行程问题有关的等量关系。
3、解题技巧:
列表或画线段图,找相等关系。
路程=速度·时间
速度=路程/时间
时间=路程/速度
(二)、师生互动、共同探究:
问题1.
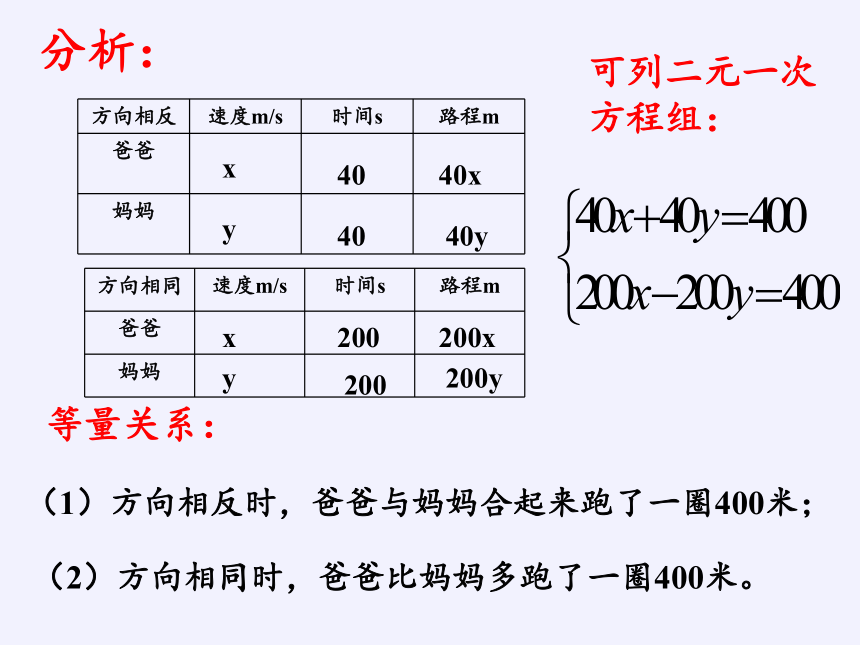
小强、爸爸、妈妈一家三口今年“五.一”期间外出郊游,因为他们有早锻炼的习惯,所以,第一天的早晨仍旧在400米的环形跑道上练习跑步,小强发现:爸爸、妈妈他们同时同地出发,如果方向相反,则40秒相遇,若两个速度不变,方向相同,那么3分20秒相遇一次,求爸爸、妈妈两人各自的速度.(爸爸比妈妈跑的快)
分析:
方向相反 速度m/s 时间s 路程m
爸爸
妈妈
方向相同 速度m/s 时间s 路程m
爸爸
妈妈
等量关系:
(1)方向相反时,爸爸与妈妈合起来跑了一圈400米;
(2)方向相同时,爸爸比妈妈多跑了一圈400米。
可列二元一次方程组:
x
x
y
y
40
40
200
200
40x
40y
200x
200y
问题2.
第一天上午,小强、爸爸、妈妈到达甲景点(公园)后,小强与爸爸两人练习跑步让妈妈当裁判,如果小强先跑10米,则爸爸跑5秒就可追上小强;如果小强先跑2秒,则爸爸跑4秒就可追上小强,若设小强的速度为x米/秒,爸爸的速度为y米/秒,则可列方程组 。
小强
爸爸
10米
5x
5y
分析:
小强
爸爸
2x
4x
4y
可列二元一次方程组:
变式练习1:
A、B两地相距20米,爸爸从A地向B地行进,同时妈妈从B地向A地行进,两秒后两人途中相遇,相遇后爸爸立即返回A地,妈妈继续向A地行进,爸爸回到A地时,妈妈离A地还有4米,求爸爸、妈妈两人的速度.
变式练习2:
妈妈从小强处出发向他左侧方向运动,同时,爸爸从小强处出发向他右侧方向运动,3秒后,相距15个单位长度,已知妈妈、爸爸的速度比是1:4。
(1).求出爸爸、妈妈的运动速度,并说出爸爸、妈妈从小强处出发运动3秒时的位置;
(2).爸爸、妈妈在3秒时的位置处同时向左侧方向运动时, 小强同时从妈妈位置出发向爸爸运动,当遇到爸爸后,立即返回向妈妈运动,遇到妈妈后又立即返回向爸爸运动,如此往返,直到爸爸追上妈妈时, 小强立即停止运动.若小强一直以20单位长度/秒的速度匀速运动,那么小强从开始运动到停止运动,行驶的路程是多少个单位长度
变式练习2:
变式练习3:
小强一家三口在郊游,第二天到达乙景点爬山,小强发现他从甲地到乙地的路有一段上坡、一段平地、一段3千米的下坡,如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需90分钟,从乙地到甲地需102分。甲地到乙地全程是多少?
问题3.
小强一家三口第二天在乙景点爬山的时候,看到远处一列火车匀速通过一个隧道后,产生了以下对话.你能根据他们的对话求出这列火车的长吗?
小强:火车开始进入隧道到完全开出隧
道共用30秒.
妈妈:整列火车完全在隧道里的时间是
20秒.
爸爸:我坐火车路过这个隧道,广播里
告诉我们隧道全长500米.
500m
ym
30x
500m
ym
20x
分析:
(1)
(2)
可列二元一次方程组:
变式练习.
两列火车分别在两条平行的铁轨上行驶,其中,快车长168m,慢车长184m,如果两车相向而行,从相遇到离开需4s;如果同向而行,从快车追上慢车到离开需16s,求两车的速度.
(三)小结:
1、今天我们学了有关行程问题的应用题,我们发现了解决这类问题的一些规律,同学们能再总结一下吗?
(1)、操场上的相遇、追击问题
(2)、平地、山坡的相遇、追击问题
(3)、火车有长度时的相遇、追击问题
2、本节课你有何收获?有何困惑?
验、答
审、设、列、解、
谢 谢
10.5 用二元一次方程组解决问题
1、会列二元一次方程组解决行程问题。
2、体会列二元一次方程组解决行程问题的一般步骤,将实际问题转化成二元一次方程组的数学模型。
教学目标:
重点、难点:
重点:1、会列二元一次方程组解决行程问题。
2、将实际问题转化成二元一次方程组
的数学模型。
难点:将实际问题转化成二元一次方程组的
数学模型。
(一)课前预习
1、列二元一次方程组解应用题的一般步骤是什么?
审 设 列 解 验 答
实际问题
数学问题
抽象
已知量、未知量,等量关系
二元一次方程组
方程组的解
解的合理性
实际问题答案
分析
列出
求出
验证
合理
设未知数
2、与行程问题有关的等量关系。
3、解题技巧:
列表或画线段图,找相等关系。
路程=速度·时间
速度=路程/时间
时间=路程/速度
(二)、师生互动、共同探究:
问题1.
小强、爸爸、妈妈一家三口今年“五.一”期间外出郊游,因为他们有早锻炼的习惯,所以,第一天的早晨仍旧在400米的环形跑道上练习跑步,小强发现:爸爸、妈妈他们同时同地出发,如果方向相反,则40秒相遇,若两个速度不变,方向相同,那么3分20秒相遇一次,求爸爸、妈妈两人各自的速度.(爸爸比妈妈跑的快)
分析:
方向相反 速度m/s 时间s 路程m
爸爸
妈妈
方向相同 速度m/s 时间s 路程m
爸爸
妈妈
等量关系:
(1)方向相反时,爸爸与妈妈合起来跑了一圈400米;
(2)方向相同时,爸爸比妈妈多跑了一圈400米。
可列二元一次方程组:
x
x
y
y
40
40
200
200
40x
40y
200x
200y
问题2.
第一天上午,小强、爸爸、妈妈到达甲景点(公园)后,小强与爸爸两人练习跑步让妈妈当裁判,如果小强先跑10米,则爸爸跑5秒就可追上小强;如果小强先跑2秒,则爸爸跑4秒就可追上小强,若设小强的速度为x米/秒,爸爸的速度为y米/秒,则可列方程组 。
小强
爸爸
10米
5x
5y
分析:
小强
爸爸
2x
4x
4y
可列二元一次方程组:
变式练习1:
A、B两地相距20米,爸爸从A地向B地行进,同时妈妈从B地向A地行进,两秒后两人途中相遇,相遇后爸爸立即返回A地,妈妈继续向A地行进,爸爸回到A地时,妈妈离A地还有4米,求爸爸、妈妈两人的速度.
变式练习2:
妈妈从小强处出发向他左侧方向运动,同时,爸爸从小强处出发向他右侧方向运动,3秒后,相距15个单位长度,已知妈妈、爸爸的速度比是1:4。
(1).求出爸爸、妈妈的运动速度,并说出爸爸、妈妈从小强处出发运动3秒时的位置;
(2).爸爸、妈妈在3秒时的位置处同时向左侧方向运动时, 小强同时从妈妈位置出发向爸爸运动,当遇到爸爸后,立即返回向妈妈运动,遇到妈妈后又立即返回向爸爸运动,如此往返,直到爸爸追上妈妈时, 小强立即停止运动.若小强一直以20单位长度/秒的速度匀速运动,那么小强从开始运动到停止运动,行驶的路程是多少个单位长度
变式练习2:
变式练习3:
小强一家三口在郊游,第二天到达乙景点爬山,小强发现他从甲地到乙地的路有一段上坡、一段平地、一段3千米的下坡,如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需90分钟,从乙地到甲地需102分。甲地到乙地全程是多少?
问题3.
小强一家三口第二天在乙景点爬山的时候,看到远处一列火车匀速通过一个隧道后,产生了以下对话.你能根据他们的对话求出这列火车的长吗?
小强:火车开始进入隧道到完全开出隧
道共用30秒.
妈妈:整列火车完全在隧道里的时间是
20秒.
爸爸:我坐火车路过这个隧道,广播里
告诉我们隧道全长500米.
500m
ym
30x
500m
ym
20x
分析:
(1)
(2)
可列二元一次方程组:
变式练习.
两列火车分别在两条平行的铁轨上行驶,其中,快车长168m,慢车长184m,如果两车相向而行,从相遇到离开需4s;如果同向而行,从快车追上慢车到离开需16s,求两车的速度.
(三)小结:
1、今天我们学了有关行程问题的应用题,我们发现了解决这类问题的一些规律,同学们能再总结一下吗?
(1)、操场上的相遇、追击问题
(2)、平地、山坡的相遇、追击问题
(3)、火车有长度时的相遇、追击问题
2、本节课你有何收获?有何困惑?
验、答
审、设、列、解、
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
