高一数学《直线与平面平行的性质》
图片预览






文档简介
课件32张PPT。2.2.3直线与平面平行
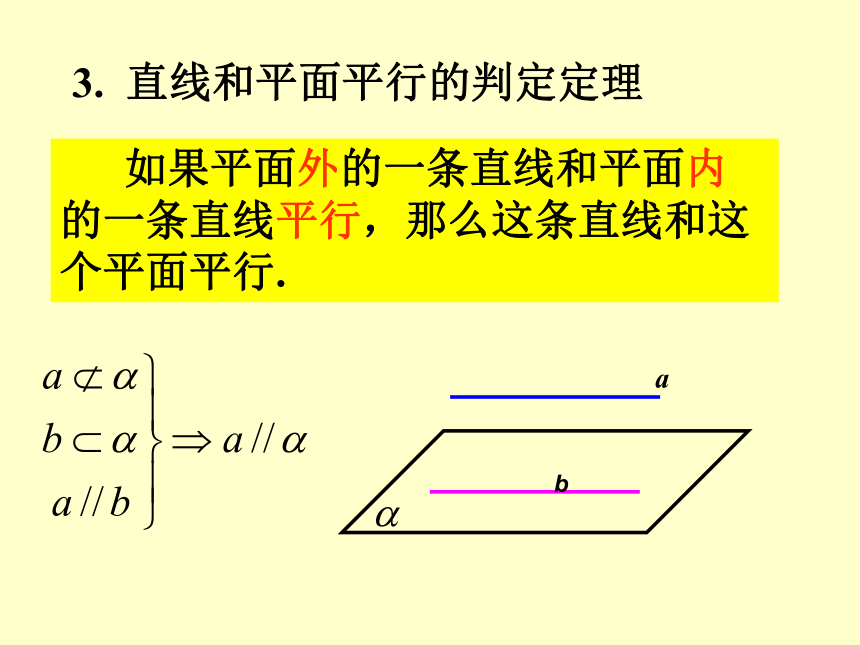
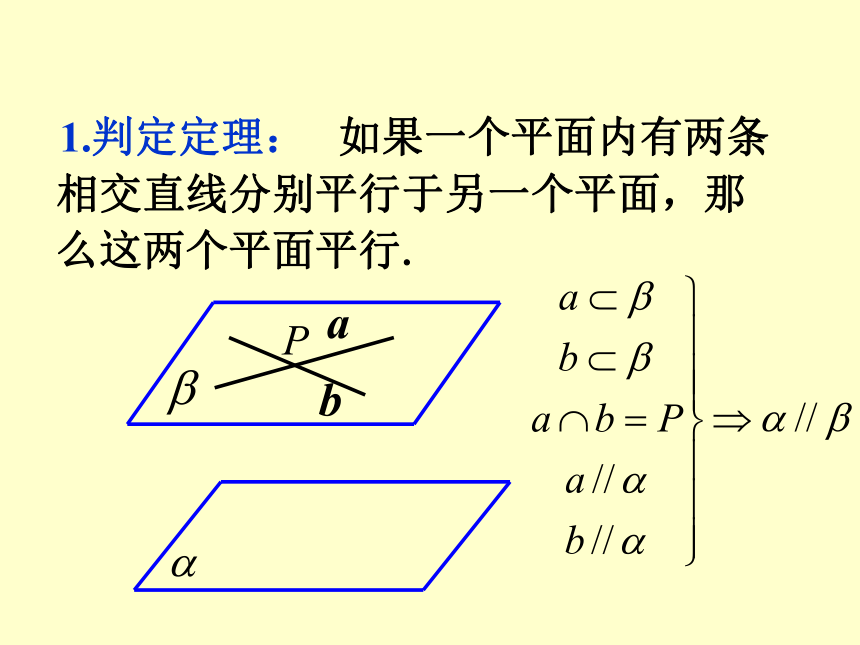
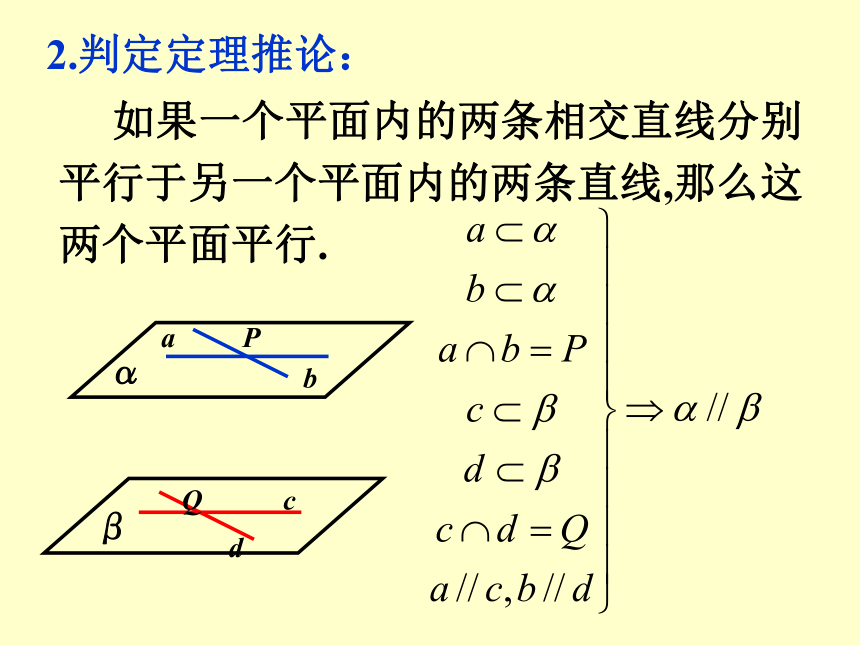
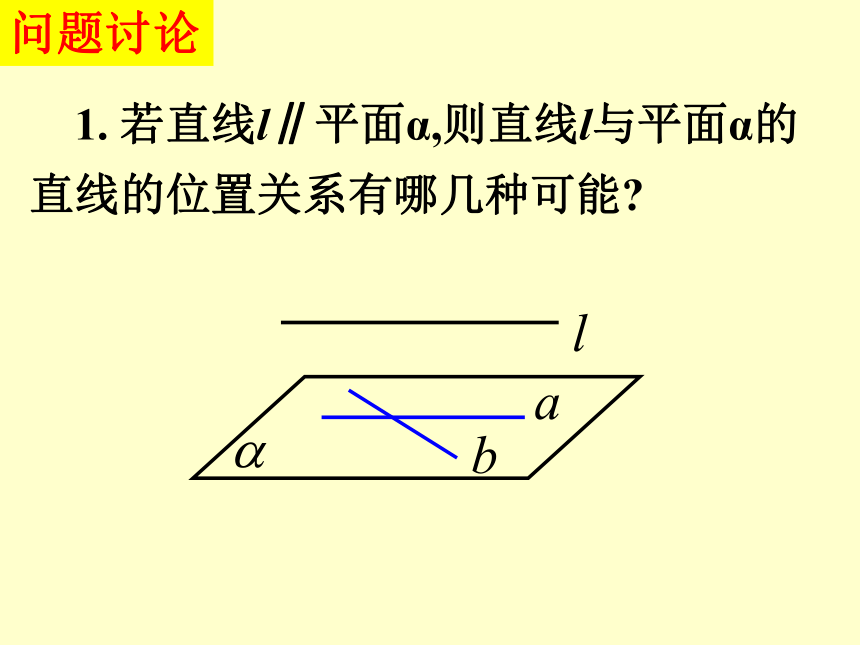
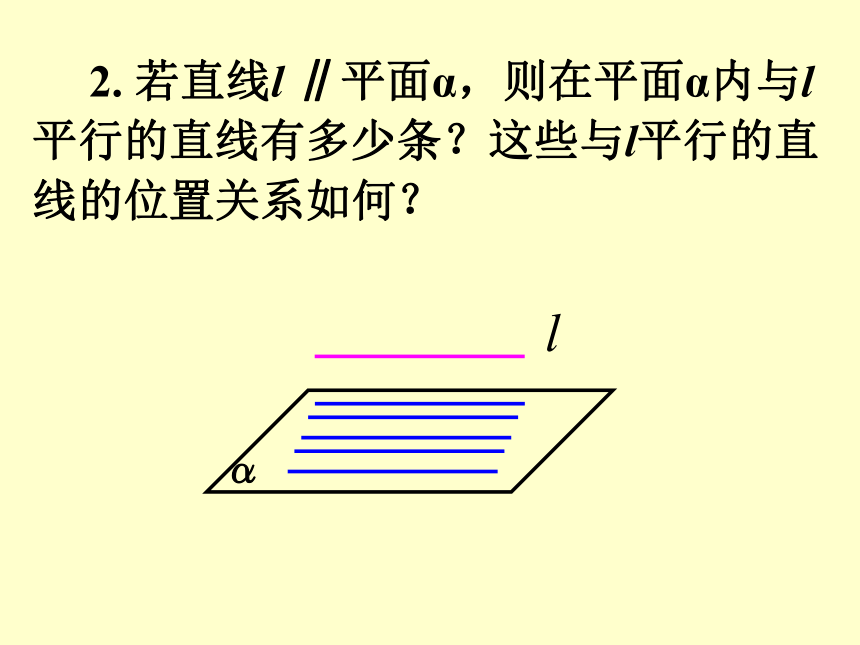
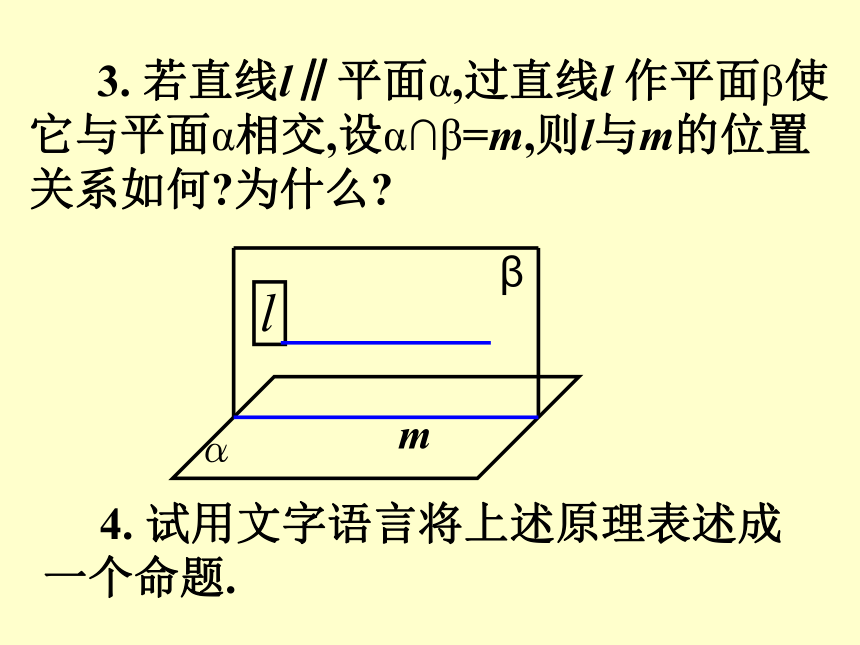
2.2.4平面与平面平行的性质1. 直线和平面有哪几种位置关系?平行、相交、在平面内 2. 反映直线和平面三种位置关系的依据是什么?公共点的个数没有公共点: 平行 仅有一个公共点:相交 无数个公共点:在平面内 复习 如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行. 3. 直线和平面平行的判定定理ab4、什么叫两平面平行?5、反应两平面平行的依据是什么? 复习 如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行.1.判定定理: 如果一个平面内的两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.2.判定定理推论:6. 线面、面面平行的判定定理解决了线面平行及面面平行的条件;反之,在直线与平面和面面平行的条件下,会得到什么结论?直线与平面、平面与平面平行的性质问题讨论 1. 若直线l∥平面α,则直线l与平面α的直线的位置关系有哪几种可能? 2. 若直线l ∥平面α,则在平面α内与l 平行的直线有多少条?这些与l平行的直线的位置关系如何? 3. 若直线l∥平面α,过直线l 作平面β使它与平面α相交,设α∩β=m,则l与m的位置关系如何?为什么? 4. 试用文字语言将上述原理表述成一个命题. 直线与平面平行的性质定理: 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.上述命题反映了直线和平面平行的一个性质,其内容可简述为“线面平行则线线平行”.若l∥α,P∈α,过点P作直线m∥l,则m与α 的位置关系如何?为什么? 问题讨论例1. 判断下列命题是否正确?(1) 若直线l 平行于平面α内的无数条直线,则l∥α.(×) 举例 (2) 设a、b为直线,α为平面,若a∥b,且b在α 内,则a∥α .(×) (3)若直线l∥平面α,则l与平面α内的任意直线都不相交. (4) 设a、b为异面直线,过直线a且与直线b平行的平面有且只有一个.(√)(√) 若 的位置关系如何? 则直线a、b的位置关系如何?为什么?平面与平面平行性质 如果两个平行平面同时和第三个平面相交, 那么它们 的交线平行.平面与平面平行性质性质定理过点A作直线 练习 (2) 若平面α、β都与平面γ相交,且交线平行,则α∥β吗?例3、求证: 夹在两个平行平面间的平行线段相等. 举例性质:夹在两个平行平面间的平行线段相等.性质:经过平面外一点有且只有一个平面和已知平面平行 两个平面平行的其它性质 归纳(A) 0 (B) 1 (C) 0或1 (D) 1或2(A)1种 (B) 2种 (C)3种 (D)4种其中可能出现的情形有 ( )1. 经过平面外两点可作该平面的平行平面的个数为( )CC 练习 平面M∥平面N,直线a M,直线b N, 下面四种情形: (1)a ∥ b (2)a ⊥ b
(3)a与b异面 (4)a与b相交例4、如图,设AB、CD为夹在两个平行平面 、 之间的线段,且直线AB、CD为异面直线,M、P 分别为AB、CD 的中点,求证:直线MP // 平面 . 举例 例5.在四面体ABCD中,E、F分别是AB、AC的中点,过直线EF作平面α,分别交BD、CD于M、N,求证:EF∥MN. 举例 例6. 如图,已知AB∥平面α,AC∥BD,且AC、BD与平面α相交于C、D,求证:AC=BD. 举例 例7. 设平面α、β、γ两两相交,且
若a∥b,求证:b∥c . 举例1. 复习直线与平面、平面与平面的位置关系
2. 复习直线与平面、平面与平面平行的判定
3. 学习并掌握直线与平面、平面与平面平行的性质 小结
2.2.4平面与平面平行的性质1. 直线和平面有哪几种位置关系?平行、相交、在平面内 2. 反映直线和平面三种位置关系的依据是什么?公共点的个数没有公共点: 平行 仅有一个公共点:相交 无数个公共点:在平面内 复习 如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行. 3. 直线和平面平行的判定定理ab4、什么叫两平面平行?5、反应两平面平行的依据是什么? 复习 如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行.1.判定定理: 如果一个平面内的两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.2.判定定理推论:6. 线面、面面平行的判定定理解决了线面平行及面面平行的条件;反之,在直线与平面和面面平行的条件下,会得到什么结论?直线与平面、平面与平面平行的性质问题讨论 1. 若直线l∥平面α,则直线l与平面α的直线的位置关系有哪几种可能? 2. 若直线l ∥平面α,则在平面α内与l 平行的直线有多少条?这些与l平行的直线的位置关系如何? 3. 若直线l∥平面α,过直线l 作平面β使它与平面α相交,设α∩β=m,则l与m的位置关系如何?为什么? 4. 试用文字语言将上述原理表述成一个命题. 直线与平面平行的性质定理: 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.上述命题反映了直线和平面平行的一个性质,其内容可简述为“线面平行则线线平行”.若l∥α,P∈α,过点P作直线m∥l,则m与α 的位置关系如何?为什么? 问题讨论例1. 判断下列命题是否正确?(1) 若直线l 平行于平面α内的无数条直线,则l∥α.(×) 举例 (2) 设a、b为直线,α为平面,若a∥b,且b在α 内,则a∥α .(×) (3)若直线l∥平面α,则l与平面α内的任意直线都不相交. (4) 设a、b为异面直线,过直线a且与直线b平行的平面有且只有一个.(√)(√) 若 的位置关系如何? 则直线a、b的位置关系如何?为什么?平面与平面平行性质 如果两个平行平面同时和第三个平面相交, 那么它们 的交线平行.平面与平面平行性质性质定理过点A作直线 练习 (2) 若平面α、β都与平面γ相交,且交线平行,则α∥β吗?例3、求证: 夹在两个平行平面间的平行线段相等. 举例性质:夹在两个平行平面间的平行线段相等.性质:经过平面外一点有且只有一个平面和已知平面平行 两个平面平行的其它性质 归纳(A) 0 (B) 1 (C) 0或1 (D) 1或2(A)1种 (B) 2种 (C)3种 (D)4种其中可能出现的情形有 ( )1. 经过平面外两点可作该平面的平行平面的个数为( )CC 练习 平面M∥平面N,直线a M,直线b N, 下面四种情形: (1)a ∥ b (2)a ⊥ b
(3)a与b异面 (4)a与b相交例4、如图,设AB、CD为夹在两个平行平面 、 之间的线段,且直线AB、CD为异面直线,M、P 分别为AB、CD 的中点,求证:直线MP // 平面 . 举例 例5.在四面体ABCD中,E、F分别是AB、AC的中点,过直线EF作平面α,分别交BD、CD于M、N,求证:EF∥MN. 举例 例6. 如图,已知AB∥平面α,AC∥BD,且AC、BD与平面α相交于C、D,求证:AC=BD. 举例 例7. 设平面α、β、γ两两相交,且
若a∥b,求证:b∥c . 举例1. 复习直线与平面、平面与平面的位置关系
2. 复习直线与平面、平面与平面平行的判定
3. 学习并掌握直线与平面、平面与平面平行的性质 小结
