青岛版 六年级数学下册 第二单元《圆柱和圆锥》综合练习 (含答案)
文档属性
| 名称 | 青岛版 六年级数学下册 第二单元《圆柱和圆锥》综合练习 (含答案) | 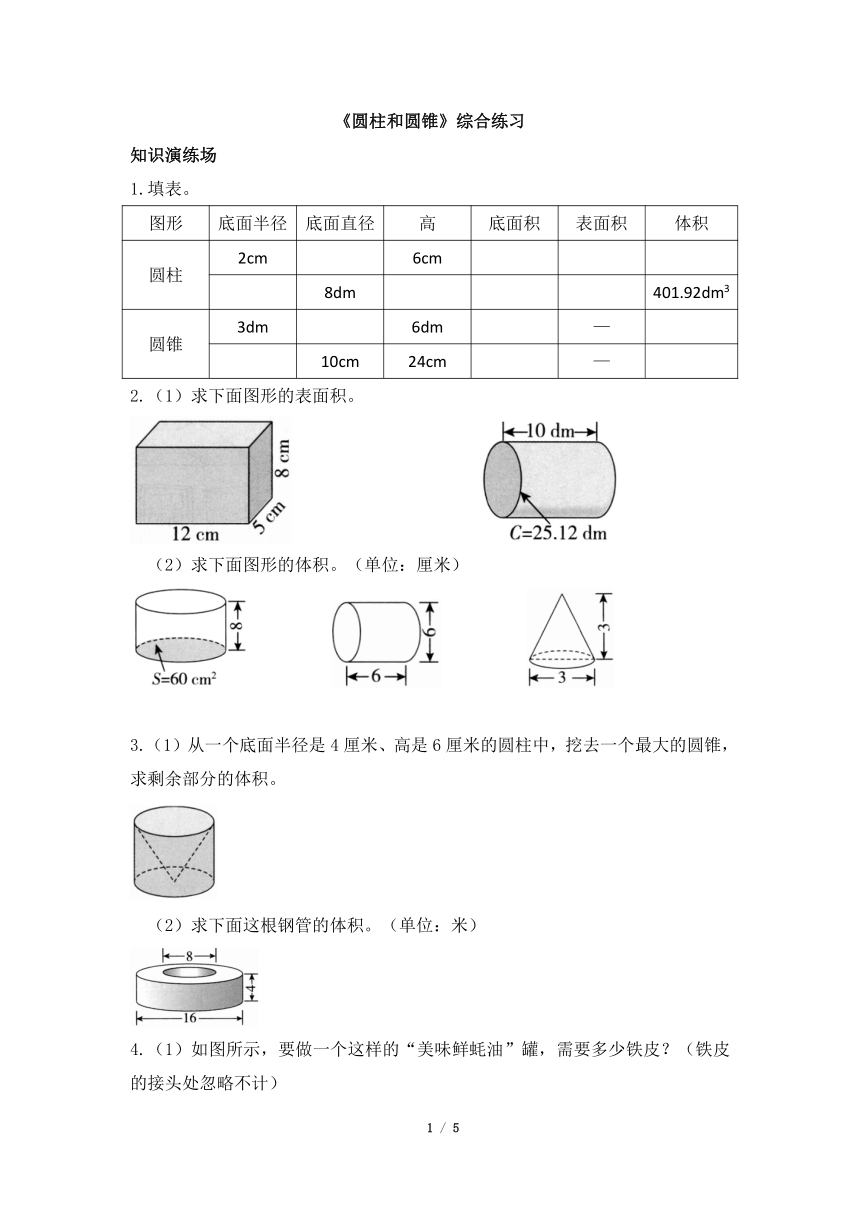 | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 20:57:21 | ||
图片预览

文档简介
《圆柱和圆锥》综合练习
知识演练场
1.填表。
图形 底面半径 底面直径 高 底面积 表面积 体积
圆柱 2cm 6cm
8dm 401.92dm3
圆锥 3dm 6dm —
10cm 24cm —
2.(1)求下面图形的表面积。
(2)求下面图形的体积。(单位:厘米)
3.(1)从一个底面半径是4厘米、高是6厘米的圆柱中,挖去一个最大的圆锥,求剩余部分的体积。
(2)求下面这根钢管的体积。(单位:米)
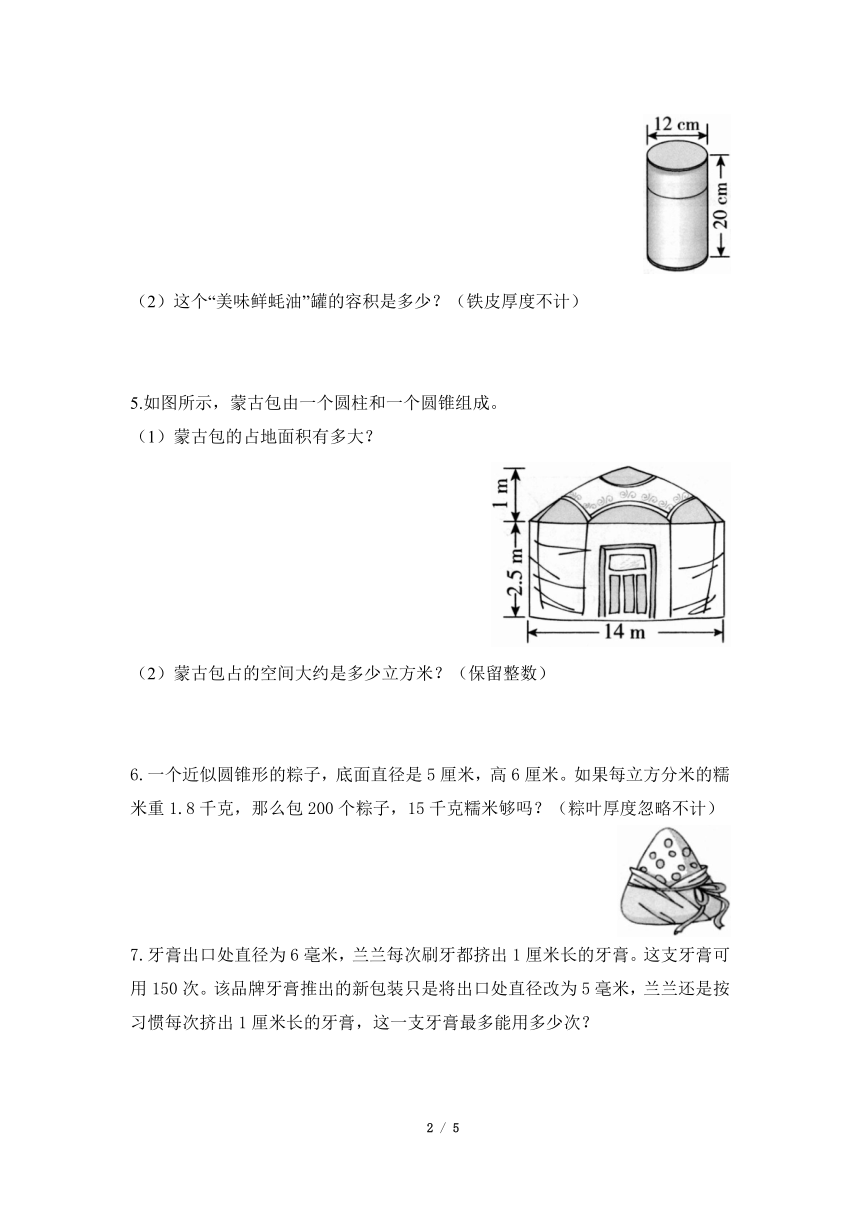
4.(1)如图所示,要做一个这样的“美味鲜蚝油”罐,需要多少铁皮?(铁皮的接头处忽略不计)
(2)这个“美味鲜蚝油”罐的容积是多少?(铁皮厚度不计)
5.如图所示,蒙古包由一个圆柱和一个圆锥组成。
(1)蒙古包的占地面积有多大?
(2)蒙古包占的空间大约是多少立方米?(保留整数)
6.一个近似圆锥形的粽子,底面直径是5厘米,高6厘米。如果每立方分米的糯米重1.8千克,那么包200个粽子,15千克糯米够吗?(粽叶厚度忽略不计)
7.牙膏出口处直径为6毫米,兰兰每次刷牙都挤出1厘米长的牙膏。这支牙膏可用150次。该品牌牙膏推出的新包装只是将出口处直径改为5毫米,兰兰还是按习惯每次挤出1厘米长的牙膏,这一支牙膏最多能用多少次?
智慧加油站
8.一个圆柱(如图所示),如果把它截短2厘米,它的表面积就比原来减少了25.12平方厘米,这个圆柱原来的体积是多少立方厘米?
参考答案:
1.(横排)4cm 12.56cm2 100.48cm2 75.36cm3 4dm 8dm 50.24dm2
301.44dm2 6dm 28.26dm2 56.52dm3 5cm 78.5cm2 628cm3
2.(1)(12×5+8×5+12×8)×2=392(cm2)
3.14×(25.12÷3.14÷2)2×2+25.12×10=351.68(dm2)
(2)60×8=480(立方厘米)
3.14×(6÷2)2×6=169.56(立方厘米)
3.14×(3÷2)2×3×=7.065(立方厘米)
3.(1)3.14×42×6×=200.96(立方厘米)
答:剩余部分的体积是200.96立方厘米。
(2)3.14×[(16÷2)2-(8÷2)2]×4=602.88(立方米)
答:下面这根钢管的体积是602.88立方米。
4.(1)3.14×(12÷2)2×2+3.14×12×20=979.68(平方厘米)
答:需要979.68平方厘米铁皮。
(2)3.14×(12÷2)2×20=2260.8(立方厘米)
答:这个“美味鲜蚝油”罐的容积是2260.8立方厘米。
5.(1)3.14×(14÷2)2=153.86(平方米)
答:蒙古包的占地面积有153.86平方米。
(2)153.86×2.5+153.86×1×≈436(立方米)
答:蒙古包占的空间大约是436立方米。
6.3.14×(5÷2)2×6×=39.25(立方厘米)
39.25×200=7850(立方厘米)
7850立方厘米≈7.85立方分米
7.85×1.8=14.13(千克) 14.13<15 答:15千克糯米够。
7.5毫米=0.5厘米 6毫米=0.6厘米
3.14×(0.6÷2)2×1×150=42.39(立方厘米)
3.14×(0.5÷2)2×1=0.19625(立方厘米)
42.39÷0.19625=216(次) 答:这一支牙膏最多能用216次。
8.25.12÷2=12.56(厘米) 12.56÷3.14÷2=2(厘米)
3.14×22×12=150.72(立方厘米)
答:这个圆柱原来的体积是150.72立方厘米。
解析 本题考查了圆柱的侧面积与体积计算公式的实际灵活应用。由“如果把它截短2厘米,它的表面积就比原来减少了25.12平方厘米”知,表面积减少的部分实际是圆柱的一部分侧面积,这部分圆柱的高是2厘米,先根据侧面积=底面周长×高,列算式25.12÷2=12.56(厘米)求出这个圆柱的底面周长是12.56厘米,然后根据圆的周长计算公式列算式12.56÷3.14÷2=2(厘米)求出这个圆柱的底面半径,最后根据圆柱的体积公式V=xr2求出这个圆柱的体积是150.72立方厘米。
4 / 5
知识演练场
1.填表。
图形 底面半径 底面直径 高 底面积 表面积 体积
圆柱 2cm 6cm
8dm 401.92dm3
圆锥 3dm 6dm —
10cm 24cm —
2.(1)求下面图形的表面积。
(2)求下面图形的体积。(单位:厘米)
3.(1)从一个底面半径是4厘米、高是6厘米的圆柱中,挖去一个最大的圆锥,求剩余部分的体积。
(2)求下面这根钢管的体积。(单位:米)
4.(1)如图所示,要做一个这样的“美味鲜蚝油”罐,需要多少铁皮?(铁皮的接头处忽略不计)
(2)这个“美味鲜蚝油”罐的容积是多少?(铁皮厚度不计)
5.如图所示,蒙古包由一个圆柱和一个圆锥组成。
(1)蒙古包的占地面积有多大?
(2)蒙古包占的空间大约是多少立方米?(保留整数)
6.一个近似圆锥形的粽子,底面直径是5厘米,高6厘米。如果每立方分米的糯米重1.8千克,那么包200个粽子,15千克糯米够吗?(粽叶厚度忽略不计)
7.牙膏出口处直径为6毫米,兰兰每次刷牙都挤出1厘米长的牙膏。这支牙膏可用150次。该品牌牙膏推出的新包装只是将出口处直径改为5毫米,兰兰还是按习惯每次挤出1厘米长的牙膏,这一支牙膏最多能用多少次?
智慧加油站
8.一个圆柱(如图所示),如果把它截短2厘米,它的表面积就比原来减少了25.12平方厘米,这个圆柱原来的体积是多少立方厘米?
参考答案:
1.(横排)4cm 12.56cm2 100.48cm2 75.36cm3 4dm 8dm 50.24dm2
301.44dm2 6dm 28.26dm2 56.52dm3 5cm 78.5cm2 628cm3
2.(1)(12×5+8×5+12×8)×2=392(cm2)
3.14×(25.12÷3.14÷2)2×2+25.12×10=351.68(dm2)
(2)60×8=480(立方厘米)
3.14×(6÷2)2×6=169.56(立方厘米)
3.14×(3÷2)2×3×=7.065(立方厘米)
3.(1)3.14×42×6×=200.96(立方厘米)
答:剩余部分的体积是200.96立方厘米。
(2)3.14×[(16÷2)2-(8÷2)2]×4=602.88(立方米)
答:下面这根钢管的体积是602.88立方米。
4.(1)3.14×(12÷2)2×2+3.14×12×20=979.68(平方厘米)
答:需要979.68平方厘米铁皮。
(2)3.14×(12÷2)2×20=2260.8(立方厘米)
答:这个“美味鲜蚝油”罐的容积是2260.8立方厘米。
5.(1)3.14×(14÷2)2=153.86(平方米)
答:蒙古包的占地面积有153.86平方米。
(2)153.86×2.5+153.86×1×≈436(立方米)
答:蒙古包占的空间大约是436立方米。
6.3.14×(5÷2)2×6×=39.25(立方厘米)
39.25×200=7850(立方厘米)
7850立方厘米≈7.85立方分米
7.85×1.8=14.13(千克) 14.13<15 答:15千克糯米够。
7.5毫米=0.5厘米 6毫米=0.6厘米
3.14×(0.6÷2)2×1×150=42.39(立方厘米)
3.14×(0.5÷2)2×1=0.19625(立方厘米)
42.39÷0.19625=216(次) 答:这一支牙膏最多能用216次。
8.25.12÷2=12.56(厘米) 12.56÷3.14÷2=2(厘米)
3.14×22×12=150.72(立方厘米)
答:这个圆柱原来的体积是150.72立方厘米。
解析 本题考查了圆柱的侧面积与体积计算公式的实际灵活应用。由“如果把它截短2厘米,它的表面积就比原来减少了25.12平方厘米”知,表面积减少的部分实际是圆柱的一部分侧面积,这部分圆柱的高是2厘米,先根据侧面积=底面周长×高,列算式25.12÷2=12.56(厘米)求出这个圆柱的底面周长是12.56厘米,然后根据圆的周长计算公式列算式12.56÷3.14÷2=2(厘米)求出这个圆柱的底面半径,最后根据圆柱的体积公式V=xr2求出这个圆柱的体积是150.72立方厘米。
4 / 5
