高一数学《直线与平面平行的判定》
文档属性
| 名称 | 高一数学《直线与平面平行的判定》 |  | |
| 格式 | zip | ||
| 文件大小 | 130.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-22 15:39:50 | ||
图片预览



文档简介
课件18张PPT。 2.2.1平行关系的判定(一)
——直线与平面平行的判定教学目标:掌握直线与平面平行的判定定理.
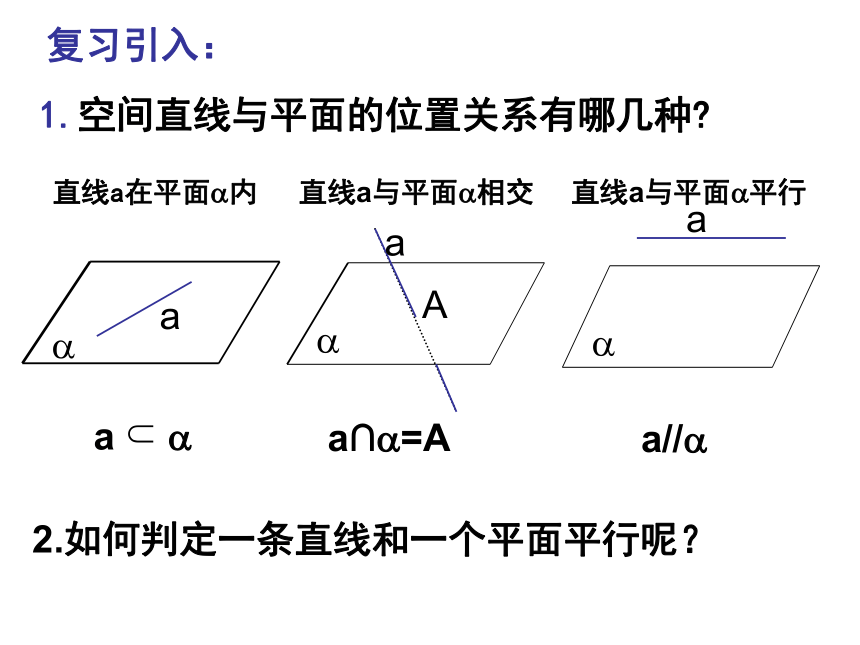
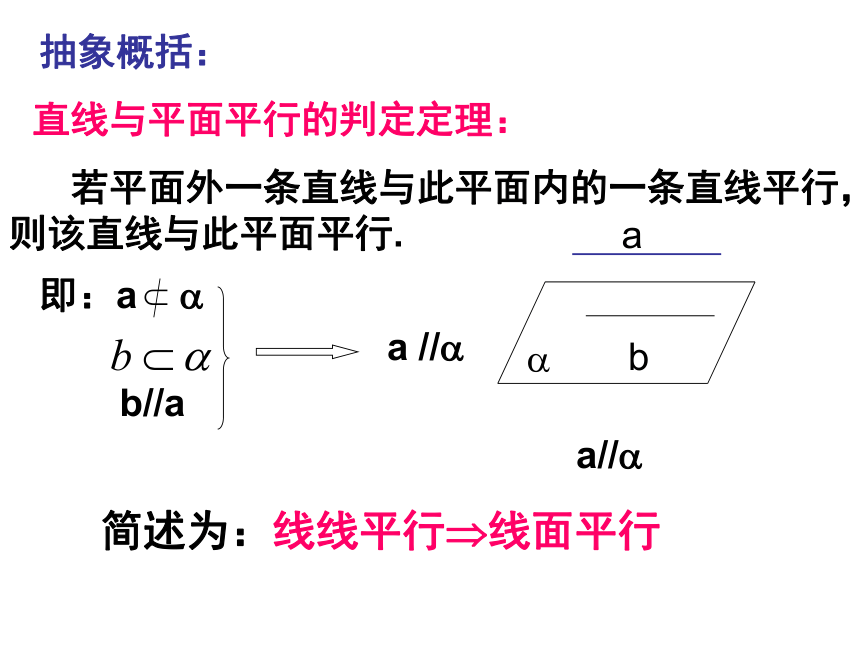
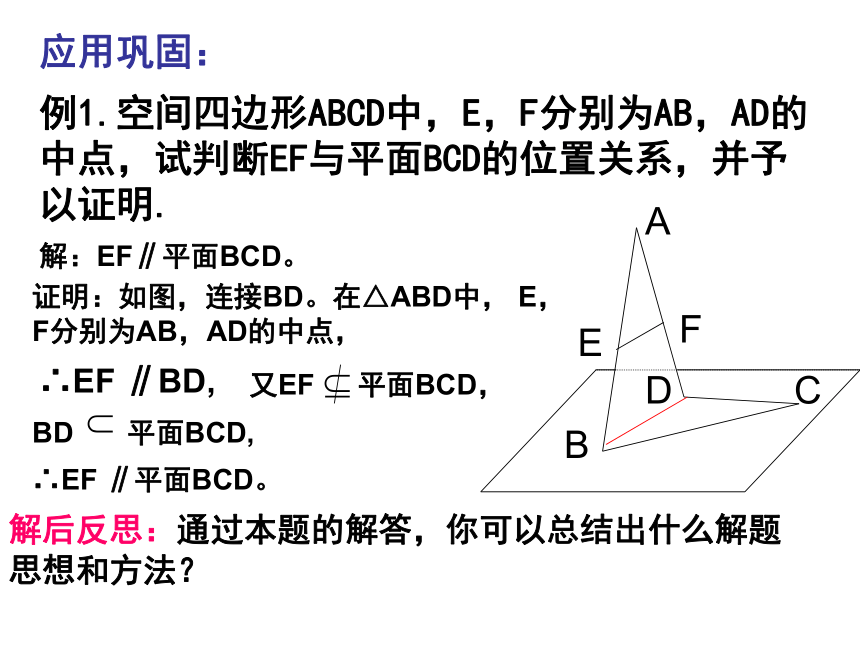
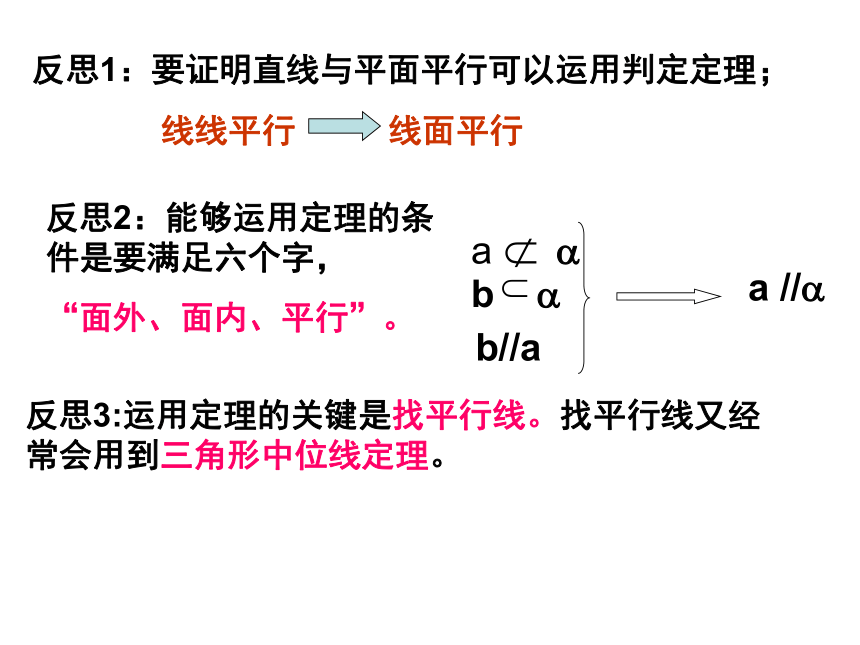
教学重点:直线与平面平行的判定定理的应用.1.空间直线与平面的位置关系有哪几种?复习引入:2.如何判定一条直线和一个平面平行呢?实例探究:抽象概括:直线与平面平行的判定定理: 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.简述为:线线平行?线面平行应用巩固:例1.空间四边形ABCD中,E,F分别为AB,AD的中点,试判断EF与平面BCD的位置关系,并予以证明.解:EF∥平面BCD。证明:如图,连接BD。在△ABD中, E,F分别为AB,AD的中点,∴EF ∥BD,∴EF ∥平面BCD。解后反思:通过本题的解答,你可以总结出什么解题思想和方法?反思1:要证明直线与平面平行可以运用判定定理;反思2:能够运用定理的条件是要满足六个字,
“面外、面内、平行”。反思3:运用定理的关键是找平行线。找平行线又经常会用到三角形中位线定理。 例2. 如图,四面体ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点.(3)你能说出图中满足线面平行位置
关系的所有情况吗?(1)E、F、G、H四点是否共面?(2)试判断AC与平面EFGH的位置关系;解:(1)E、F、G、H四点共面。∵在△ABD中,E、H分别是AB、AD的中点.∴EH∥BD且同理GF ∥BD且EH ∥GF且EH=GF∴E、F、G、H四点共面。(2) AC ∥平面EFGH(3)由EF ∥HG ∥AC,得EF ∥平面ACDAC ∥平面EFGHHG ∥平面ABC由BD ∥EH ∥FG,得BD∥平面EFGHEH ∥平面BCDFG ∥平面ABD如图,正方体 中,P 是棱A1B1 的中点,过点 P 画一条直线使之与截面A1BCD1 平行.思考交流:如何证明线面平行?关键:找平行线课堂练习1、如图,在正方体ABCD——A1B1C1D1六个表面中,
(Ⅰ)与AB平行的直线有:
(Ⅱ)与AB平行的平面有: A1B1、CD、C1D1平面A1C1、平面D1C2、如图,在长方体ABCD——A1B1C1D1中,E为DD1的中点。试判断BD1与平面AEC的位置关系,并说明理由。 F3、如图,在正方体ABCD——A1B1C1D1中,E、F分别是棱BC与C1D1的中点。
求证:EF//平面BDD1B1.MNM2.应用判定定理判定线面平行时应注意六个字:
(1)面外,(2)面内,(3)平行。小结:1.直线与平面平行的判定:3.应用判定定理判定线面平行的关键是找平行线方法一:三角形的中位线定理;方法二:平行四边形的平行关系。1、如何证明面面平行呢?课外探讨:2、如图,已知有公共边AB的两个全等矩形ABCD和ABEF不在同一个平面内,P、Q是对角线AE、BD上的动点。
当P、Q满足什么条件时,
PQ∥平面CBE?再 见
——直线与平面平行的判定教学目标:掌握直线与平面平行的判定定理.
教学重点:直线与平面平行的判定定理的应用.1.空间直线与平面的位置关系有哪几种?复习引入:2.如何判定一条直线和一个平面平行呢?实例探究:抽象概括:直线与平面平行的判定定理: 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.简述为:线线平行?线面平行应用巩固:例1.空间四边形ABCD中,E,F分别为AB,AD的中点,试判断EF与平面BCD的位置关系,并予以证明.解:EF∥平面BCD。证明:如图,连接BD。在△ABD中, E,F分别为AB,AD的中点,∴EF ∥BD,∴EF ∥平面BCD。解后反思:通过本题的解答,你可以总结出什么解题思想和方法?反思1:要证明直线与平面平行可以运用判定定理;反思2:能够运用定理的条件是要满足六个字,
“面外、面内、平行”。反思3:运用定理的关键是找平行线。找平行线又经常会用到三角形中位线定理。 例2. 如图,四面体ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点.(3)你能说出图中满足线面平行位置
关系的所有情况吗?(1)E、F、G、H四点是否共面?(2)试判断AC与平面EFGH的位置关系;解:(1)E、F、G、H四点共面。∵在△ABD中,E、H分别是AB、AD的中点.∴EH∥BD且同理GF ∥BD且EH ∥GF且EH=GF∴E、F、G、H四点共面。(2) AC ∥平面EFGH(3)由EF ∥HG ∥AC,得EF ∥平面ACDAC ∥平面EFGHHG ∥平面ABC由BD ∥EH ∥FG,得BD∥平面EFGHEH ∥平面BCDFG ∥平面ABD如图,正方体 中,P 是棱A1B1 的中点,过点 P 画一条直线使之与截面A1BCD1 平行.思考交流:如何证明线面平行?关键:找平行线课堂练习1、如图,在正方体ABCD——A1B1C1D1六个表面中,
(Ⅰ)与AB平行的直线有:
(Ⅱ)与AB平行的平面有: A1B1、CD、C1D1平面A1C1、平面D1C2、如图,在长方体ABCD——A1B1C1D1中,E为DD1的中点。试判断BD1与平面AEC的位置关系,并说明理由。 F3、如图,在正方体ABCD——A1B1C1D1中,E、F分别是棱BC与C1D1的中点。
求证:EF//平面BDD1B1.MNM2.应用判定定理判定线面平行时应注意六个字:
(1)面外,(2)面内,(3)平行。小结:1.直线与平面平行的判定:3.应用判定定理判定线面平行的关键是找平行线方法一:三角形的中位线定理;方法二:平行四边形的平行关系。1、如何证明面面平行呢?课外探讨:2、如图,已知有公共边AB的两个全等矩形ABCD和ABEF不在同一个平面内,P、Q是对角线AE、BD上的动点。
当P、Q满足什么条件时,
PQ∥平面CBE?再 见
