苏科版七年级数学下册 11.5 用一元一次不等式解决问题(2)教案 (表格式)
文档属性
| 名称 | 苏科版七年级数学下册 11.5 用一元一次不等式解决问题(2)教案 (表格式) | 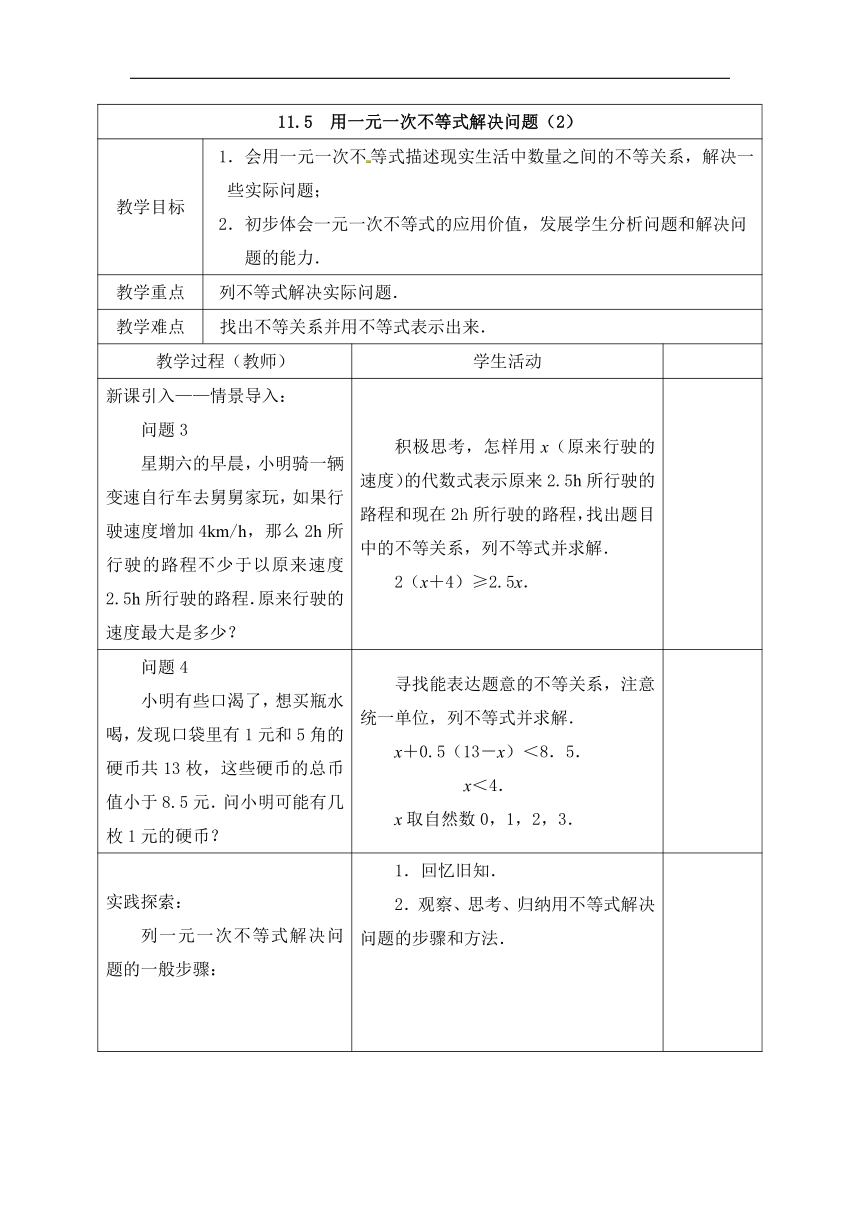 | |
| 格式 | docx | ||
| 文件大小 | 19.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 07:59:25 | ||
图片预览

文档简介
11.5 用一元一次不等式解决问题(2)
教学目标 1.会用一元一次不等式描述现实生活中数量之间的不等关系,解决一些实际问题; 2.初步体会一元一次不等式的应用价值,发展学生分析问题和解决问题的能力.
教学重点 列不等式解决实际问题.
教学难点 找出不等关系并用不等式表示出来.
教学过程(教师) 学生活动
新课引入——情景导入: 问题3 星期六的早晨,小明骑一辆变速自行车去舅舅家玩,如果行驶速度增加4km/h,那么2h所行驶的路程不少于以原来速度2.5h所行驶的路程.原来行驶的速度最大是多少? 积极思考,怎样用x(原来行驶的速度)的代数式表示原来2.5h所行驶的路程和现在2h所行驶的路程,找出题目中的不等关系,列不等式并求解. 2(x+4)≥2.5x.
问题4 小明有些口渴了,想买瓶水喝,发现口袋里有1元和5角的硬币共13枚,这些硬币的总币值小于8.5元.问小明可能有几枚1元的硬币? 寻找能表达题意的不等关系,注意统一单位,列不等式并求解. x+0.5(13-x)<8.5. x<4. x取自然数0,1,2,3.
实践探索: 列一元一次不等式解决问题的一般步骤: 1.回忆旧知. 2.观察、思考、归纳用不等式解决问题的步骤和方法.
练习1 小明舅舅是某工地爆破员,他想考一下小明,他说:工地爆破时导火线的燃烧速度是0.8cm/s,点燃导火线的人要在爆破时跑到200米以外的安全区域.如果引爆人跑步的速度是5米/秒,那么导火线长度应大于多少? 理解题意,根据用不等式解决问题的步骤和方法列不等式并解答. 参考答案:应大于32cm.
练习2 午饭前,小明和表哥一起看足球比赛直播,小明想考一考和自己同年的表哥:甲、乙两队进行足球对抗赛,比赛规则规定每对胜一场得3分,平一场得1分,负一场得0分.两队一共比赛了10场,甲队保持不败,得分超过22分.甲队至少胜了多少场? 发表意见,表达观点,相互补充. 参考答案:至少胜了7场.
小结: 1.一元一次不等式解决问题有哪些步骤? 2.用一元一次不等式解决问题的关键是什么? 有针对性地对知识点进行小结.
课后作业: 1.书P133习题1、2、3、4. 2.《补充习题》用一元一次不等式解决问题(2). 课后完成.
教学目标 1.会用一元一次不等式描述现实生活中数量之间的不等关系,解决一些实际问题; 2.初步体会一元一次不等式的应用价值,发展学生分析问题和解决问题的能力.
教学重点 列不等式解决实际问题.
教学难点 找出不等关系并用不等式表示出来.
教学过程(教师) 学生活动
新课引入——情景导入: 问题3 星期六的早晨,小明骑一辆变速自行车去舅舅家玩,如果行驶速度增加4km/h,那么2h所行驶的路程不少于以原来速度2.5h所行驶的路程.原来行驶的速度最大是多少? 积极思考,怎样用x(原来行驶的速度)的代数式表示原来2.5h所行驶的路程和现在2h所行驶的路程,找出题目中的不等关系,列不等式并求解. 2(x+4)≥2.5x.
问题4 小明有些口渴了,想买瓶水喝,发现口袋里有1元和5角的硬币共13枚,这些硬币的总币值小于8.5元.问小明可能有几枚1元的硬币? 寻找能表达题意的不等关系,注意统一单位,列不等式并求解. x+0.5(13-x)<8.5. x<4. x取自然数0,1,2,3.
实践探索: 列一元一次不等式解决问题的一般步骤: 1.回忆旧知. 2.观察、思考、归纳用不等式解决问题的步骤和方法.
练习1 小明舅舅是某工地爆破员,他想考一下小明,他说:工地爆破时导火线的燃烧速度是0.8cm/s,点燃导火线的人要在爆破时跑到200米以外的安全区域.如果引爆人跑步的速度是5米/秒,那么导火线长度应大于多少? 理解题意,根据用不等式解决问题的步骤和方法列不等式并解答. 参考答案:应大于32cm.
练习2 午饭前,小明和表哥一起看足球比赛直播,小明想考一考和自己同年的表哥:甲、乙两队进行足球对抗赛,比赛规则规定每对胜一场得3分,平一场得1分,负一场得0分.两队一共比赛了10场,甲队保持不败,得分超过22分.甲队至少胜了多少场? 发表意见,表达观点,相互补充. 参考答案:至少胜了7场.
小结: 1.一元一次不等式解决问题有哪些步骤? 2.用一元一次不等式解决问题的关键是什么? 有针对性地对知识点进行小结.
课后作业: 1.书P133习题1、2、3、4. 2.《补充习题》用一元一次不等式解决问题(2). 课后完成.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
