沪科版九年级下24.7弧长与扇形面积(第一课时) (共22张PPT)
文档属性
| 名称 | 沪科版九年级下24.7弧长与扇形面积(第一课时) (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
24.7弧长与扇形的面积
沪科版数学九年级下
第一课时
第24章 圆
生活中的扇形
欣 赏
新课探究
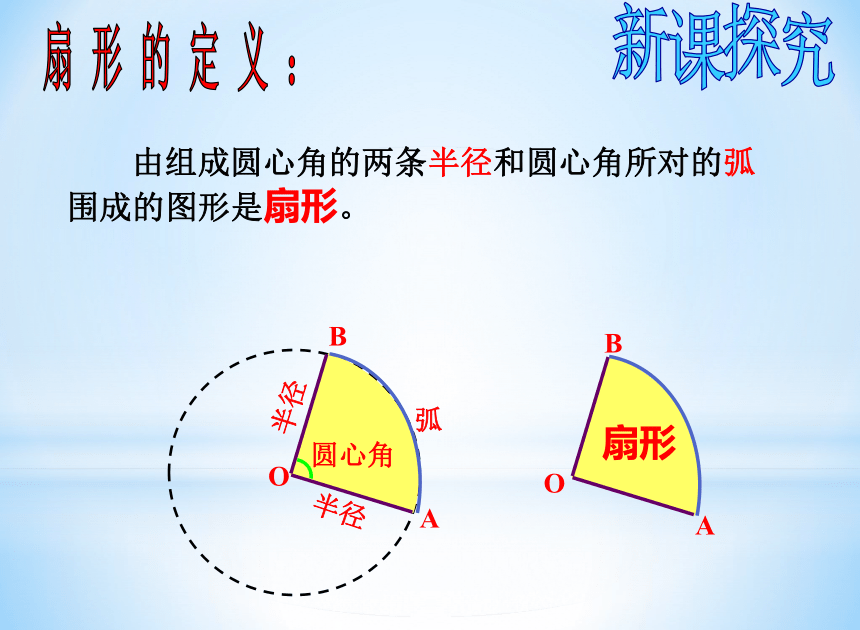
扇 形 的 定 义 :
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
新课探究
讨论1:
如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
因为要保证这些弯道的“展直长度”是一样的
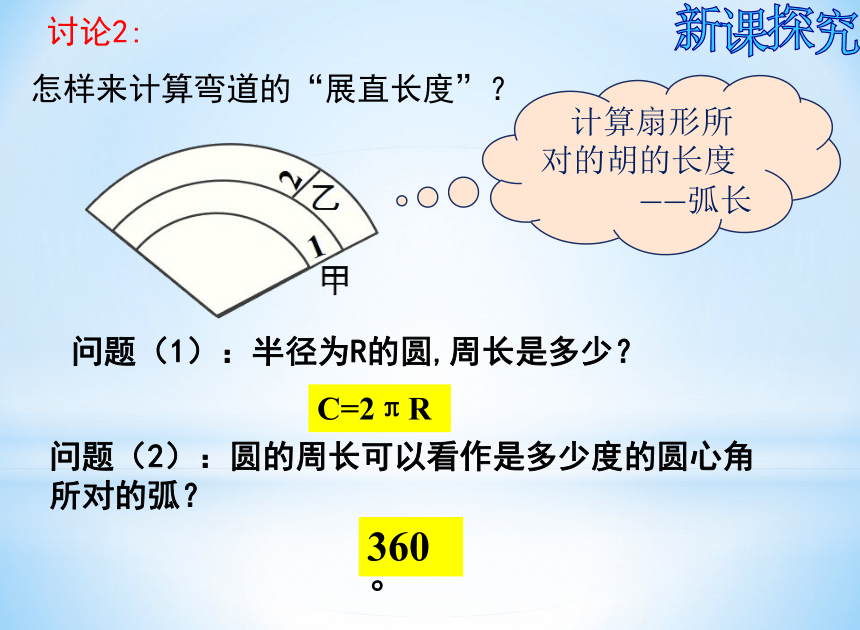
讨论2:
怎样来计算弯道的“展直长度”?
计算扇形所对的胡的长度
——弧长
问题(1):半径为R的圆,周长是多少?
C=2πR
问题(2):圆的周长可以看作是多少度的圆心角 所对的弧?
360°
新课探究
讲授新课
O
R
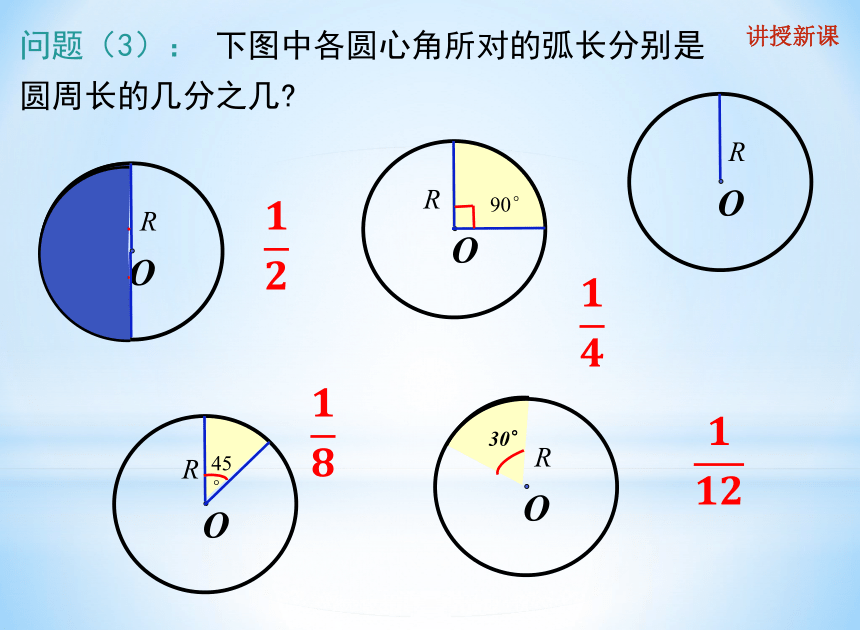
问题(3): 下图中各圆心角所对的弧长分别是圆周长的几分之几
O
R
180°
O
R
90°
O
R
45°
O
R
30°
问题(4):1°圆心角所对弧长是多少?
n°
A
B
O
若设⊙O半径为R, n°的圆心角所对的弧长为 l ,则
l弧= l圆=
360
n
新课探究
用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
注意
算一算 已知弧所对的圆心角为60°,半径是4,则弧长为____.
弧长公式
l弧= l圆=
360
n
新课讲解
例1、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
因此展直长度为
L (mm)
答:管道的展直长度为2970mm.
(mm)
解:由弧长公式,可得弧AB的长
︵
例题讲解
例2:古希腊埃拉托塞尼曾给出一个估算地球周长(或整个子午圈长)的简便方法。如图,点S和点A分别表示埃及的赛伊尼和亚历山大两地,亚历山大在赛伊尼的北方,两地的经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5m).当太阳光线在赛伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为a,他实际测得a是7.2度,由此估算出了地球的周长,你能计算吗?
C
 ̄
⌒
AS
=
360
 ̄
7.2
∴C=50
⌒
AS
=50×5000
=250000≈39625(km)
答:过南北极的地球周长约为39625km。
例题讲解
解:因为太阳光线可看作平行的,所以圆心角∠AOS=a=7.2度 设地球的周长(即⊙O的周长)为C,则
讨论3:
(1)半径为R的圆,面积是多少?
S=πR2
(3)1°圆心角所对扇形面积是多少?
(2)圆面可以看作是多少度的圆心角所对的扇形?
360°
新知再探
A
B
O
(4)若设⊙O半径为R, n°的圆心角所对的扇形面积为S,
则
新知再探
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
注意
新知讲解
___大小不变时,对应的扇形面积与 __ 有关,
___ 越长,面积越大.
圆心角
半径
半径
圆的 不变时,扇形面积与 有关, 越大,面积越大.
圆心角
半径
圆心角
总结:扇形的面积与圆心角、半径有关.
O ●
A
B
D
C
E
F
O ●
A
B
C
D
讨论4: 扇形的面积与哪些因素有关?
讨论5:扇形的弧长公式与面积公式有联系吗?
A
B
O
O
新知讲解
A
B
O
O
用弧长表示扇形面积:
新知讲解
想一想 扇形的面积公式与什么公式类似?
1.已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇形=_____l弧长=____.
公式应用
2.已知一条弧的半径为9,弧长为 8π,那么这条弧所对的圆心角为_____。
3、如果一个扇形面积是它所在圆的面积的 ,则此扇形的圆心角是( )
(A)300 (B)360 (C)450 (D)600
5、如图所示,OA=3OB,则 的长是 的长的_____倍.
AD
︵
BC
︵
4、一个扇形的弧长是20 ,面积是240 ,则扇形的圆心
角是 。
C
150°
3
已知矩形ABCD,AB=8cm,AD=4cm,以A为圆心,AB为半径画弧与CD交点M,求图中阴影面积
能力提升
N
┐
解:过M作MN⊥AB,垂足为N
∴MN=AD=4cm
∵在Rt△AMN中,AM=AB=8,
Sin∠NAM==
∴ ∠NAM=30°
∵在Rt△ADM中,由勾股定理得DM=cm
∴S△ADM =cm
S阴影=- S△ADM – S扇形 =(32-)cm
小 结 :
2. 扇形面积公式与弧长公式:
1.弧长与扇形的面积大小与哪些因素有关?
(1)与圆心角的大小有关
(2)与半径的长短有关
l弧= l圆=
360
n
S扇形= S圆=
360
n
S扇形= l r
2
1
24.7弧长与扇形的面积
沪科版数学九年级下
第一课时
第24章 圆
生活中的扇形
欣 赏
新课探究
扇 形 的 定 义 :
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
新课探究
讨论1:
如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
因为要保证这些弯道的“展直长度”是一样的
讨论2:
怎样来计算弯道的“展直长度”?
计算扇形所对的胡的长度
——弧长
问题(1):半径为R的圆,周长是多少?
C=2πR
问题(2):圆的周长可以看作是多少度的圆心角 所对的弧?
360°
新课探究
讲授新课
O
R
问题(3): 下图中各圆心角所对的弧长分别是圆周长的几分之几
O
R
180°
O
R
90°
O
R
45°
O
R
30°
问题(4):1°圆心角所对弧长是多少?
n°
A
B
O
若设⊙O半径为R, n°的圆心角所对的弧长为 l ,则
l弧= l圆=
360
n
新课探究
用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
注意
算一算 已知弧所对的圆心角为60°,半径是4,则弧长为____.
弧长公式
l弧= l圆=
360
n
新课讲解
例1、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
因此展直长度为
L (mm)
答:管道的展直长度为2970mm.
(mm)
解:由弧长公式,可得弧AB的长
︵
例题讲解
例2:古希腊埃拉托塞尼曾给出一个估算地球周长(或整个子午圈长)的简便方法。如图,点S和点A分别表示埃及的赛伊尼和亚历山大两地,亚历山大在赛伊尼的北方,两地的经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5m).当太阳光线在赛伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为a,他实际测得a是7.2度,由此估算出了地球的周长,你能计算吗?
C
 ̄
⌒
AS
=
360
 ̄
7.2
∴C=50
⌒
AS
=50×5000
=250000≈39625(km)
答:过南北极的地球周长约为39625km。
例题讲解
解:因为太阳光线可看作平行的,所以圆心角∠AOS=a=7.2度 设地球的周长(即⊙O的周长)为C,则
讨论3:
(1)半径为R的圆,面积是多少?
S=πR2
(3)1°圆心角所对扇形面积是多少?
(2)圆面可以看作是多少度的圆心角所对的扇形?
360°
新知再探
A
B
O
(4)若设⊙O半径为R, n°的圆心角所对的扇形面积为S,
则
新知再探
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
注意
新知讲解
___大小不变时,对应的扇形面积与 __ 有关,
___ 越长,面积越大.
圆心角
半径
半径
圆的 不变时,扇形面积与 有关, 越大,面积越大.
圆心角
半径
圆心角
总结:扇形的面积与圆心角、半径有关.
O ●
A
B
D
C
E
F
O ●
A
B
C
D
讨论4: 扇形的面积与哪些因素有关?
讨论5:扇形的弧长公式与面积公式有联系吗?
A
B
O
O
新知讲解
A
B
O
O
用弧长表示扇形面积:
新知讲解
想一想 扇形的面积公式与什么公式类似?
1.已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇形=_____l弧长=____.
公式应用
2.已知一条弧的半径为9,弧长为 8π,那么这条弧所对的圆心角为_____。
3、如果一个扇形面积是它所在圆的面积的 ,则此扇形的圆心角是( )
(A)300 (B)360 (C)450 (D)600
5、如图所示,OA=3OB,则 的长是 的长的_____倍.
AD
︵
BC
︵
4、一个扇形的弧长是20 ,面积是240 ,则扇形的圆心
角是 。
C
150°
3
已知矩形ABCD,AB=8cm,AD=4cm,以A为圆心,AB为半径画弧与CD交点M,求图中阴影面积
能力提升
N
┐
解:过M作MN⊥AB,垂足为N
∴MN=AD=4cm
∵在Rt△AMN中,AM=AB=8,
Sin∠NAM==
∴ ∠NAM=30°
∵在Rt△ADM中,由勾股定理得DM=cm
∴S△ADM =cm
S阴影=- S△ADM – S扇形 =(32-)cm
小 结 :
2. 扇形面积公式与弧长公式:
1.弧长与扇形的面积大小与哪些因素有关?
(1)与圆心角的大小有关
(2)与半径的长短有关
l弧= l圆=
360
n
S扇形= S圆=
360
n
S扇形= l r
2
1
