高二数学 正弦、余弦函数的性质(奇偶性、单调性、最值)
文档属性
| 名称 | 高二数学 正弦、余弦函数的性质(奇偶性、单调性、最值) |  | |
| 格式 | zip | ||
| 文件大小 | 248.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-22 19:36:26 | ||
图片预览



文档简介
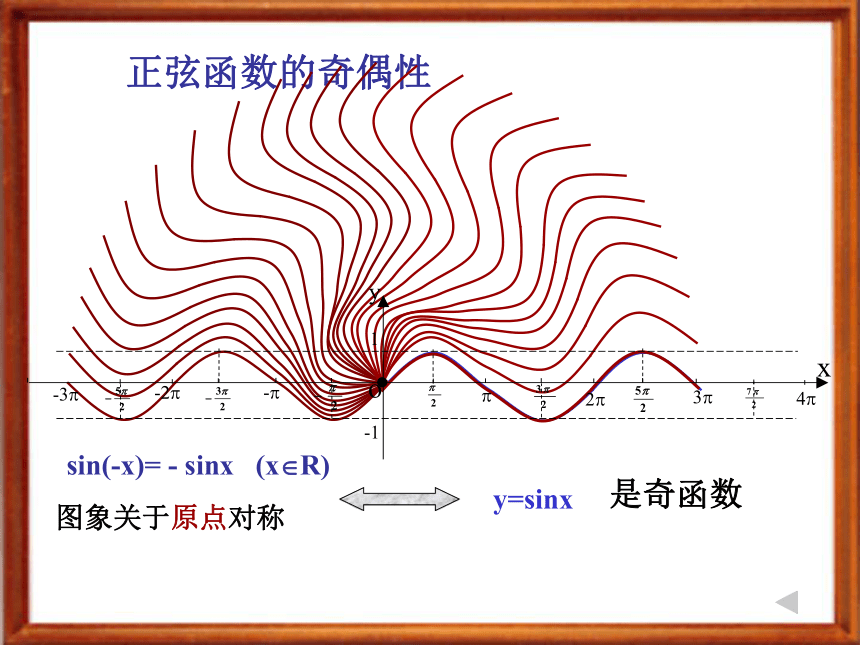
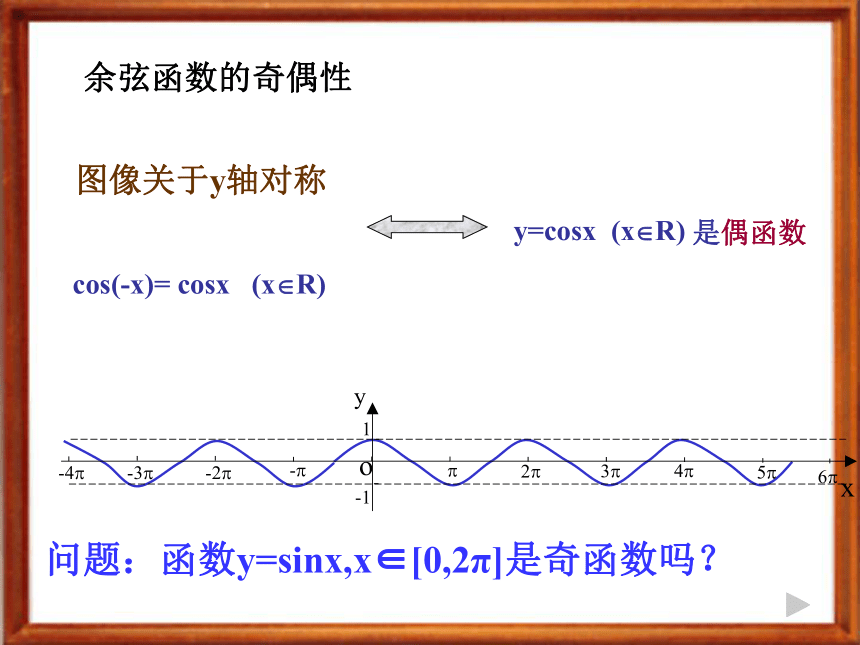
课件14张PPT。 正弦、余弦函数的性质(奇偶性、单调性、最值)高一年级:曹静哈密市高级中学 正弦函数的奇偶性 y=sinx 图象关于原点对称是奇函数sin(-x)= - sinx (x?R) cos(-x)= cosx (x?R) y=cosx (x?R)是偶函数 余弦函数的奇偶性图像关于y轴对称问题:函数y=sinx,x∈[0,2π]是奇函数吗?
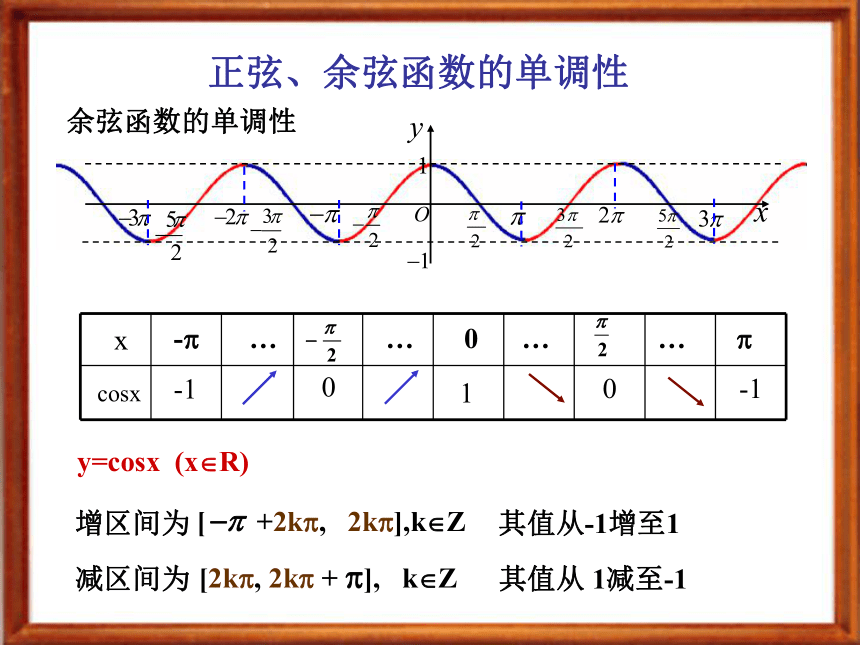
练习:判定下列函数的奇偶性 正弦、余弦函数的奇偶性 1、2、 正弦、余弦函数的单调性 正弦函数的单调性 y=sinx (x?R)增区间为 [ , ] 其值从-1增至1 … 0 … … ? …-1 0 1 0 -1减区间为 [ , ] 其值从 1减至-1[ +2k?, +2k?],k?Z[ +2k?, +2k?],k?Z 正弦、余弦函数的单调性 余弦函数的单调性 y=cosx (x?R) -? … … 0 … … ?-1 0 1 0 -1正弦函数的最大值和最小值 最大值:有最大值最小值:当 时,有最小值当 时,余弦函数的最大值和最小值最大值:当 时,有最大值最小值:当 时,有最小值例1.下列函数有最大、最小值吗?如果有,请写出取最大、最小值时的自变量x的集合,并说出最大、最小值分别是什么.解:这两个函数都有最大值、最小值.(1)使函数 取得最大值的x的集合,就是使函数 取得最大值的x的集合 使函数 取得最小值的x的集合,就是
使函数 取得最小值的x的集合 函数 的最大值是1+1=2;最小值是
-1+1=0.解:(2)令t=2x,因为使函数 取最大值的t的集合是所以使函数 取最大值的x的集合是同理,使函数 取最小值的x的集合是函数 取最大值是3,最小值是-3。 正弦、余弦函数的单调性 例2、利用三角函数的单调性,比较下列各组数的大小:
(1) sin( ) 、sin( )(2) cos( ) 、 cos( ) 解:?又 y=sinx 在 上是增函数解:?又 y=cosx 在 上是减函数cos( )=cos =cos cos( )=cos =cos 小 结: 正弦、余弦函数的奇偶性、单调性、最值 奇偶性 单调性(单调区间)奇函数偶函数[ +2k?, +2k?],k?Z单调递增[ +2k?, +2k?],k?Z单调递减函数正弦、余弦函数的最值正弦函数的最大值与最小值:
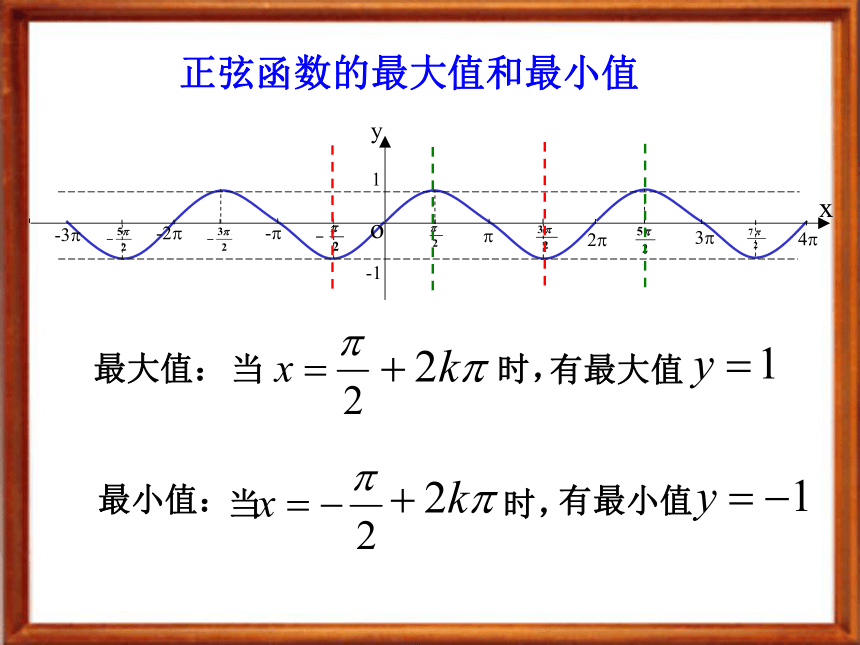
(1) 当sinx=1,即x=2kπ+ (k∈Z)时,ymax=1;
(2) 当sinx=-1,即x=2kπ- (k∈Z)时,ymax=-1。
余弦函数的最大值与最小值:
(1) 当cosx=1,即x=2kπ(k∈Z)时,ymax=1;
(2) 当cosx=-1,即x=2kπ+π(k∈Z)时,ymax=-1。作业课本58页习题4.8 第5、6、7题
练习:判定下列函数的奇偶性 正弦、余弦函数的奇偶性 1、2、 正弦、余弦函数的单调性 正弦函数的单调性 y=sinx (x?R)增区间为 [ , ] 其值从-1增至1 … 0 … … ? …-1 0 1 0 -1减区间为 [ , ] 其值从 1减至-1[ +2k?, +2k?],k?Z[ +2k?, +2k?],k?Z 正弦、余弦函数的单调性 余弦函数的单调性 y=cosx (x?R) -? … … 0 … … ?-1 0 1 0 -1正弦函数的最大值和最小值 最大值:有最大值最小值:当 时,有最小值当 时,余弦函数的最大值和最小值最大值:当 时,有最大值最小值:当 时,有最小值例1.下列函数有最大、最小值吗?如果有,请写出取最大、最小值时的自变量x的集合,并说出最大、最小值分别是什么.解:这两个函数都有最大值、最小值.(1)使函数 取得最大值的x的集合,就是使函数 取得最大值的x的集合 使函数 取得最小值的x的集合,就是
使函数 取得最小值的x的集合 函数 的最大值是1+1=2;最小值是
-1+1=0.解:(2)令t=2x,因为使函数 取最大值的t的集合是所以使函数 取最大值的x的集合是同理,使函数 取最小值的x的集合是函数 取最大值是3,最小值是-3。 正弦、余弦函数的单调性 例2、利用三角函数的单调性,比较下列各组数的大小:
(1) sin( ) 、sin( )(2) cos( ) 、 cos( ) 解:?又 y=sinx 在 上是增函数解:?又 y=cosx 在 上是减函数cos( )=cos =cos cos( )=cos =cos 小 结: 正弦、余弦函数的奇偶性、单调性、最值 奇偶性 单调性(单调区间)奇函数偶函数[ +2k?, +2k?],k?Z单调递增[ +2k?, +2k?],k?Z单调递减函数正弦、余弦函数的最值正弦函数的最大值与最小值:
(1) 当sinx=1,即x=2kπ+ (k∈Z)时,ymax=1;
(2) 当sinx=-1,即x=2kπ- (k∈Z)时,ymax=-1。
余弦函数的最大值与最小值:
(1) 当cosx=1,即x=2kπ(k∈Z)时,ymax=1;
(2) 当cosx=-1,即x=2kπ+π(k∈Z)时,ymax=-1。作业课本58页习题4.8 第5、6、7题
