人教版数学九年级下册 26.1反比例函数 课件(共33张PPT)
文档属性
| 名称 | 人教版数学九年级下册 26.1反比例函数 课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 861.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 08:23:26 | ||
图片预览







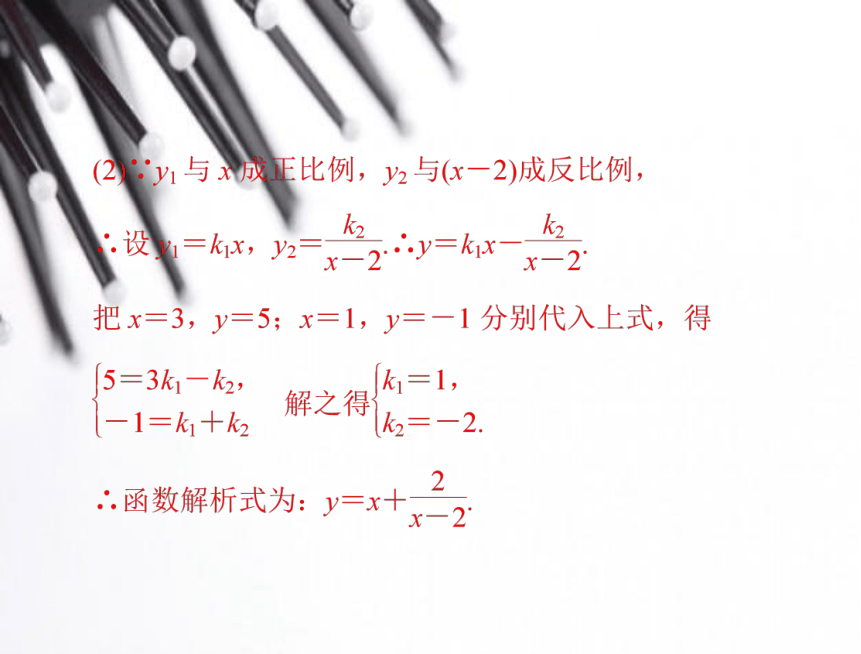




文档简介
(共33张PPT)
第二十六章
反比例函数
第1课时 反比例函数
26.1 反比例函数
1.反比例函数的定义
(1)形如_____________________的函数,叫做反比例函数,
其中 x 是________,y 是函数.
自变量
(2)自变量 x 的取值范围是_________的一切实数.
2.“待定系数法”确定函数解析式
若 y 是 x 的一次函数,则设 y=___________________;
若 y 是 x 的正比例函数,则设 y=_________________;
若 y 是 x 的反比例函数,则设 y=_________________.
不等于 0
kx+b(k为常数,k≠0)
kx(k为常数,k≠0)
知识点 1
反比例函数的定义
【例 1】判别下列式子是否表示 y 是关于 x 的反比例函数?
如果是,请指出相应的 k 值是多少?
思路点拨:根据定义进行判断.
解:②⑤⑨是反比例函数,k 值分别为-5,123,3.
反比例函数定义式及常见的变式(k 为常数,
【跟踪训练】
1.下列函数中,是反比例函数的是(
)
D
2.已知函数 y=kxk-2 是反比例函数,求 k 的值.
解:由题意得,k-2=-1 且 k≠0,解得 k=1.
知识点 2
求反比例函数解析式(重点)
【例 2】 (1)已知变量 y 与 x 成反比例,并且当 x=3 时,y
=7,①写出 y 与 x 之间的函数解析式;②求当 x=7 时函数的
值;
(2)已知函数 y=y1-y2,y1 与 x 成正比例,y2 与(x-2)成反
比例,且当 x=3 时,y=5;当 x=1 时,y=-1,求出 y 与 x
的函数解析式.
(2)y2与(x-2)成反比例中,学会把(x-2)看作一个整体.
【跟踪训练】
为__________.
2
4.如图 26-1-1,某反比例函数的图象过点(-2,1),则此反
)
图 26-1-1
B
比例函数的解析式为(
第2课时
反比例函数的图象和性质
探究:y= (k≠0)可变形为 k=__________.
1.反比例函数的图象
xy
(1)当 k>0 时,由于______得正,因此可以判断 x,y 的符号
________,所以点(x,y)在____________象限,所以函数图象位
于__________象限.
相同
第一或第三
一、三
xy
(2)当 k<0 时,由于__________得负,因此可以判断 x,y
的符号________,所以点(x,y)在____________象限,所以函数
图象位于__________象限.
二、四
归纳:反比例函数的图象是_______,它有_____分支.
两个
当 k>0 时,函数图象位于____________象限;
当 k<0 时,函数图象位于____________象限.
xy
相反
第二或第四
双曲线
一、三
二、四
2.反比例函数的性质
(1)形状:________线.
双曲
(2)位置:k>0 时,图象在第________象限;
一、三
k<0 时,图象在第________象限.
二、四
(3)增减性:
k>0 时,在每一个象限内,y 随 x 的增大而______;
k<0 时,在每一个象限内,y 随 x 的增大而______.
减小
增大
知识点 1
反比例函数的图象及画法(重点)
x -4 -3 -2 -1 1 2 3 4
y=
-1
-
-2 -4 4 2
1
y=-
1
2 4 -4 -2
-
-1
解:列表:
描点、连线,如图 D54.
图 D54
(1)其两个分支关于原点对称.
x 轴对称,也关于 y 轴对称.
画图象时注意:①双曲线的两支是断开的,
因为 x≠0;②双曲线的两端呈“无限接近坐标轴”但永远不与
坐标轴相交;③一般分别在每支曲线上取四到五个点,取的点
越多,图象越精确.
【跟踪训练】
1.图 26-1-2 是我们学过的反比例函数图象,它的函数解
析式可能是(
)
图 26-1-2
B
A.y=x2
图象大致是(
)
B
知识点 2
反比例函数的性质(重难点)
y2),(x3,y3),其中 x1关系.
解:∵k=6>0,∴函数图象在第一、三象限.
∵x1∴(x1,y1),(x2,y2)在第三象限,(x3,y3)在第一象限.
∴y1<0,y2<0,y3>0.
∵k>0时,在每个象限内y随x的增大而减小,
∴y2∴y2(1)反比例函数的增减性不是连续的,因此在
涉及反比例函数的增减性时,一般都是指在各自象限内的增减
情况.
(2)反比例函数图象的位置和函数的增减性,都是由反比例
系数 k 的符号决定的;反过来,由双曲线的位置和函数的增减
性,也可以推断出 k 的符号.
(3)解决反比例函数的相关问题时,往往我们需要画出函数
的大致图象(即草图)采用数形结合的方法,解决问题更直观.
3.若函数 y=
【跟踪训练】
m+2
x
的图象在其象限内 y 的值随 x 值的增大
B
而增大,则 m 的取值范围是(
A.m>-2
C.m>2
)
B.m<-2
D.m<2
解析:反比例函数在其象限内 y 的值随 x 值的增大而增大,
则需要 m+2<0,所以 m<-2.
图象的一个分支,对于给出的下列说法:
图 26-1-3
①常数 k 的取值范围是 k>2;
②另一个分支在第三象限;
③在函数图象上取点 A(a1 ,b1)和点 B(a2 ,b2),当 a1 >a2
时,则 b1<b2;
④在函数图象的某一个分支上取点 A(a1,b1)和点 B(a2,b2),
当 a1>a2 时,则 b1<b2.
其中正确的是 __________(在横线上填出正确的序号).
①②④
知识点 3
k 的几何意义(知识拓展)
【例 3】 过如图 26-1-4 所示双曲线上任一点 P 作 x 轴、y
轴的垂线 PM、PN,求四边形 PMON 的面积.
图 26-1-4
若 P 在第四象限,或双曲线在第一、三象限,
则同样有 S 四边形PMON=|k|.
因此 k 的几何意义为:过双曲线上任意一点作 x 轴、y 轴的
垂线,所得的四边形的面积为|k|.
【跟踪训练】
图 26-1-5
为此图象上的一动点,过点 A 分别作 AB⊥x 轴和 AC⊥y 轴,垂
足分别为 B,C,则四边形 OBAC 周长的最小值为(
)
A.4
B.3
C.2
D.1
解析:要使四边形的周长最小,则需要四边形为正方形,
此时 OB=AB=AC=OC=1,所以周长为 4.
A
的图象交于点 M(a,1),MN⊥x 轴于点N(如图 26-1-6),若△OMN
的面积等于 2,求这两个函数的解析式.
图 26-1-6
第二十六章
反比例函数
第1课时 反比例函数
26.1 反比例函数
1.反比例函数的定义
(1)形如_____________________的函数,叫做反比例函数,
其中 x 是________,y 是函数.
自变量
(2)自变量 x 的取值范围是_________的一切实数.
2.“待定系数法”确定函数解析式
若 y 是 x 的一次函数,则设 y=___________________;
若 y 是 x 的正比例函数,则设 y=_________________;
若 y 是 x 的反比例函数,则设 y=_________________.
不等于 0
kx+b(k为常数,k≠0)
kx(k为常数,k≠0)
知识点 1
反比例函数的定义
【例 1】判别下列式子是否表示 y 是关于 x 的反比例函数?
如果是,请指出相应的 k 值是多少?
思路点拨:根据定义进行判断.
解:②⑤⑨是反比例函数,k 值分别为-5,123,3.
反比例函数定义式及常见的变式(k 为常数,
【跟踪训练】
1.下列函数中,是反比例函数的是(
)
D
2.已知函数 y=kxk-2 是反比例函数,求 k 的值.
解:由题意得,k-2=-1 且 k≠0,解得 k=1.
知识点 2
求反比例函数解析式(重点)
【例 2】 (1)已知变量 y 与 x 成反比例,并且当 x=3 时,y
=7,①写出 y 与 x 之间的函数解析式;②求当 x=7 时函数的
值;
(2)已知函数 y=y1-y2,y1 与 x 成正比例,y2 与(x-2)成反
比例,且当 x=3 时,y=5;当 x=1 时,y=-1,求出 y 与 x
的函数解析式.
(2)y2与(x-2)成反比例中,学会把(x-2)看作一个整体.
【跟踪训练】
为__________.
2
4.如图 26-1-1,某反比例函数的图象过点(-2,1),则此反
)
图 26-1-1
B
比例函数的解析式为(
第2课时
反比例函数的图象和性质
探究:y= (k≠0)可变形为 k=__________.
1.反比例函数的图象
xy
(1)当 k>0 时,由于______得正,因此可以判断 x,y 的符号
________,所以点(x,y)在____________象限,所以函数图象位
于__________象限.
相同
第一或第三
一、三
xy
(2)当 k<0 时,由于__________得负,因此可以判断 x,y
的符号________,所以点(x,y)在____________象限,所以函数
图象位于__________象限.
二、四
归纳:反比例函数的图象是_______,它有_____分支.
两个
当 k>0 时,函数图象位于____________象限;
当 k<0 时,函数图象位于____________象限.
xy
相反
第二或第四
双曲线
一、三
二、四
2.反比例函数的性质
(1)形状:________线.
双曲
(2)位置:k>0 时,图象在第________象限;
一、三
k<0 时,图象在第________象限.
二、四
(3)增减性:
k>0 时,在每一个象限内,y 随 x 的增大而______;
k<0 时,在每一个象限内,y 随 x 的增大而______.
减小
增大
知识点 1
反比例函数的图象及画法(重点)
x -4 -3 -2 -1 1 2 3 4
y=
-1
-
-2 -4 4 2
1
y=-
1
2 4 -4 -2
-
-1
解:列表:
描点、连线,如图 D54.
图 D54
(1)其两个分支关于原点对称.
x 轴对称,也关于 y 轴对称.
画图象时注意:①双曲线的两支是断开的,
因为 x≠0;②双曲线的两端呈“无限接近坐标轴”但永远不与
坐标轴相交;③一般分别在每支曲线上取四到五个点,取的点
越多,图象越精确.
【跟踪训练】
1.图 26-1-2 是我们学过的反比例函数图象,它的函数解
析式可能是(
)
图 26-1-2
B
A.y=x2
图象大致是(
)
B
知识点 2
反比例函数的性质(重难点)
y2),(x3,y3),其中 x1
解:∵k=6>0,∴函数图象在第一、三象限.
∵x1
∴y1<0,y2<0,y3>0.
∵k>0时,在每个象限内y随x的增大而减小,
∴y2
涉及反比例函数的增减性时,一般都是指在各自象限内的增减
情况.
(2)反比例函数图象的位置和函数的增减性,都是由反比例
系数 k 的符号决定的;反过来,由双曲线的位置和函数的增减
性,也可以推断出 k 的符号.
(3)解决反比例函数的相关问题时,往往我们需要画出函数
的大致图象(即草图)采用数形结合的方法,解决问题更直观.
3.若函数 y=
【跟踪训练】
m+2
x
的图象在其象限内 y 的值随 x 值的增大
B
而增大,则 m 的取值范围是(
A.m>-2
C.m>2
)
B.m<-2
D.m<2
解析:反比例函数在其象限内 y 的值随 x 值的增大而增大,
则需要 m+2<0,所以 m<-2.
图象的一个分支,对于给出的下列说法:
图 26-1-3
①常数 k 的取值范围是 k>2;
②另一个分支在第三象限;
③在函数图象上取点 A(a1 ,b1)和点 B(a2 ,b2),当 a1 >a2
时,则 b1<b2;
④在函数图象的某一个分支上取点 A(a1,b1)和点 B(a2,b2),
当 a1>a2 时,则 b1<b2.
其中正确的是 __________(在横线上填出正确的序号).
①②④
知识点 3
k 的几何意义(知识拓展)
【例 3】 过如图 26-1-4 所示双曲线上任一点 P 作 x 轴、y
轴的垂线 PM、PN,求四边形 PMON 的面积.
图 26-1-4
若 P 在第四象限,或双曲线在第一、三象限,
则同样有 S 四边形PMON=|k|.
因此 k 的几何意义为:过双曲线上任意一点作 x 轴、y 轴的
垂线,所得的四边形的面积为|k|.
【跟踪训练】
图 26-1-5
为此图象上的一动点,过点 A 分别作 AB⊥x 轴和 AC⊥y 轴,垂
足分别为 B,C,则四边形 OBAC 周长的最小值为(
)
A.4
B.3
C.2
D.1
解析:要使四边形的周长最小,则需要四边形为正方形,
此时 OB=AB=AC=OC=1,所以周长为 4.
A
的图象交于点 M(a,1),MN⊥x 轴于点N(如图 26-1-6),若△OMN
的面积等于 2,求这两个函数的解析式.
图 26-1-6
