4.1.1认识三角形 课件(共39张PPT)
文档属性
| 名称 | 4.1.1认识三角形 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 00:00:00 | ||
图片预览




文档简介
(共39张PPT)
4.1.1 认识三角形
北师大版七年级下册数学
第四章 三角形
在我们日常生活中经常能看到三角形的影子.
减速慢行
注意儿童
前方村庄
情景引入
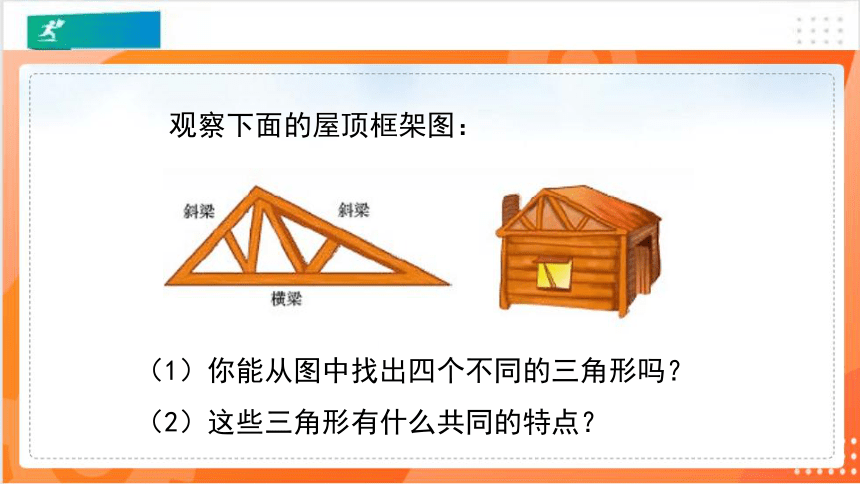
观察下面的屋顶框架图:
(1)你能从图中找出四个不同的三角形吗?
(2)这些三角形有什么共同的特点?
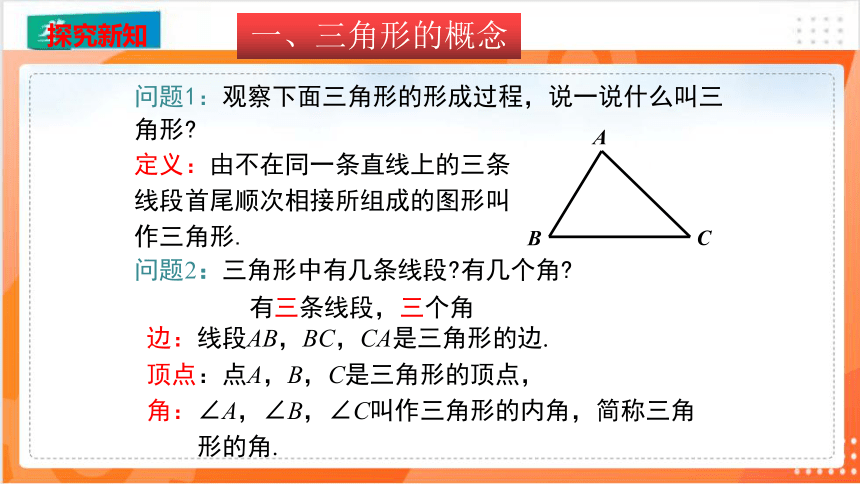
问题1:观察下面三角形的形成过程,说一说什么叫三角形
定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫作三角形.
问题2:三角形中有几条线段 有几个角
A
B
C
边:线段AB,BC,CA是三角形的边.
顶点:点A,B,C是三角形的顶点,
角:∠A,∠B,∠C叫作三角形的内角,简称三角
形的角.
有三条线段,三个角
一、三角形的概念
探究新知
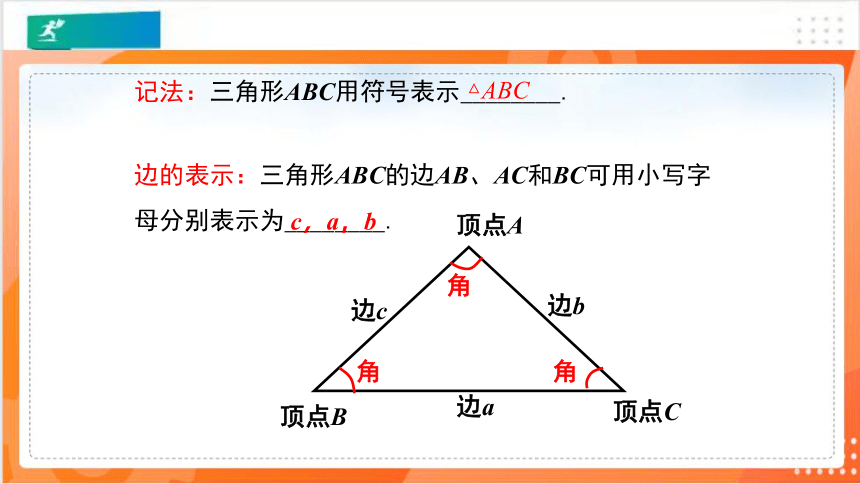
记法:三角形ABC用符号表示________.
边的表示:三角形ABC的边AB、AC和BC可用小写字母分别表示为________.
△ABC
c,a,b
边c
边b
边a
顶点C
角
角
角
顶点A
顶点B
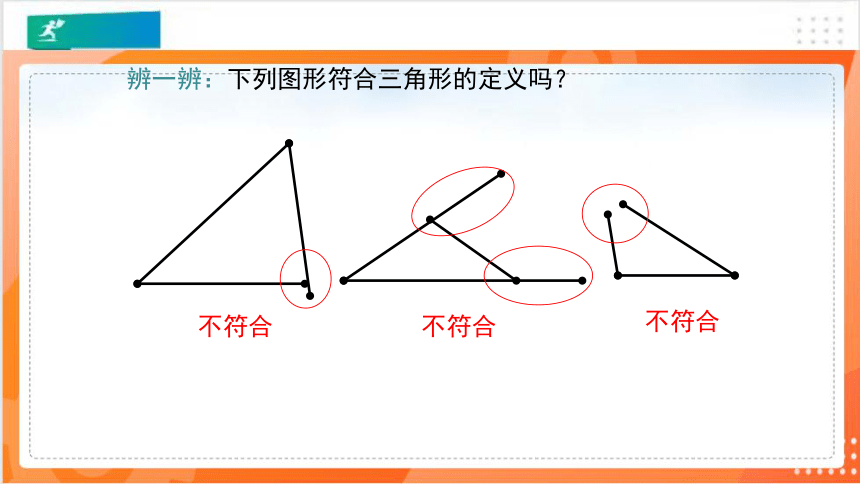
辨一辨:下列图形符合三角形的定义吗?
不符合
不符合
不符合
①位置关系:不在同一直线上;
②联接方式:首尾顺次相接.
三角形应满足以下两个条件:
要点提醒
表示方法:
三角形用符号“△”表示;记作“△ABC”,读作“三角形ABC”,除此△ABC还可记作△BCA,
△ CAB, △ ACB等.
基本要素:
三角形的边:边AB、BC、CA;
三角形的顶点:顶点A、B、C;
三角形的内角(简称为三角形的角):∠ A、 ∠ B、 ∠ C.
特别规定:
三角形ABC的三边,一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c.
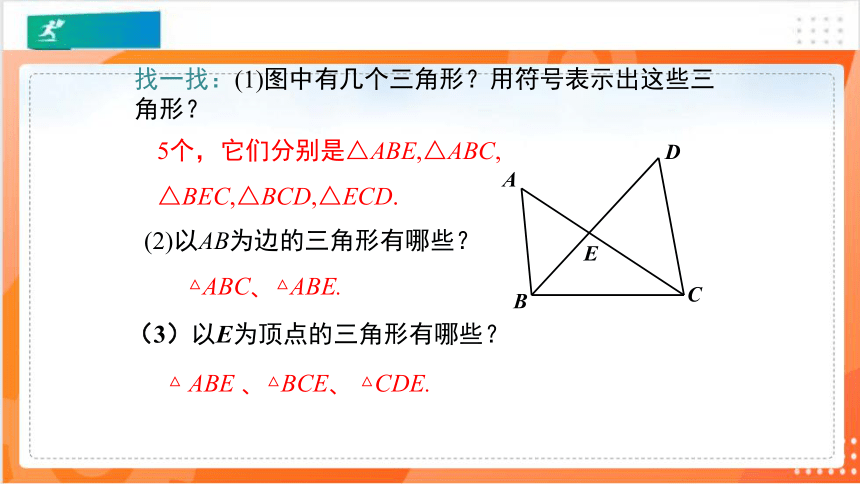
5个,它们分别是△ABE,△ABC, △BEC,△BCD,△ECD.
找一找:(1)图中有几个三角形?用符号表示出这些三角形?
A
B
C
D
E
(2)以AB为边的三角形有哪些?
△ABC、△ABE.
(3)以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △CDE.
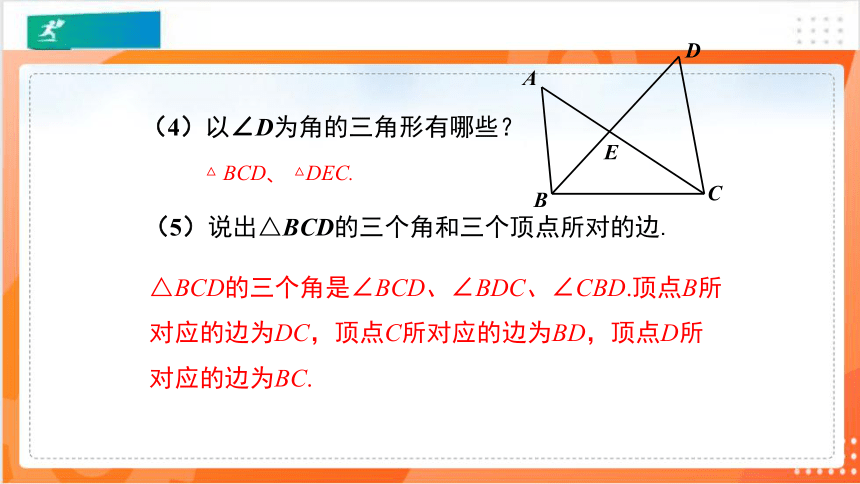
(4)以∠D为角的三角形有哪些?
△ BCD、 △DEC.
(5)说出△BCD的三个角和三个顶点所对的边.
△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.
A
B
C
D
E
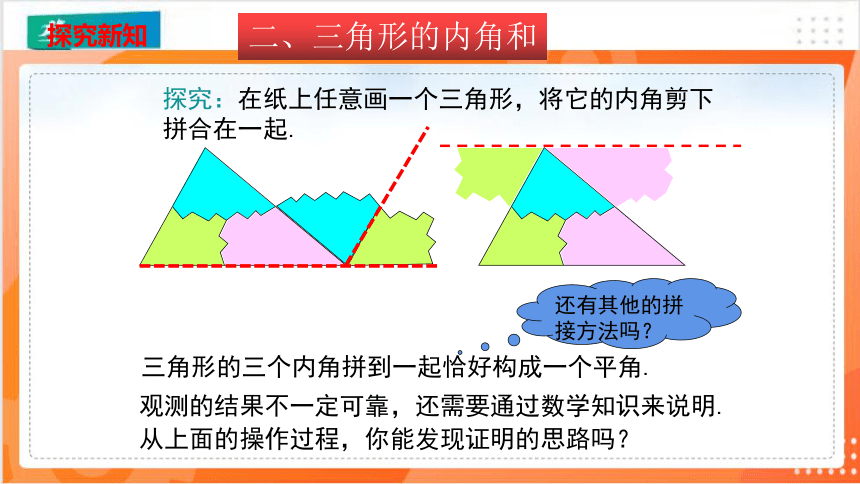
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
还有其他的拼接方法吗?
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
二、三角形的内角和
探究新知
验证结论
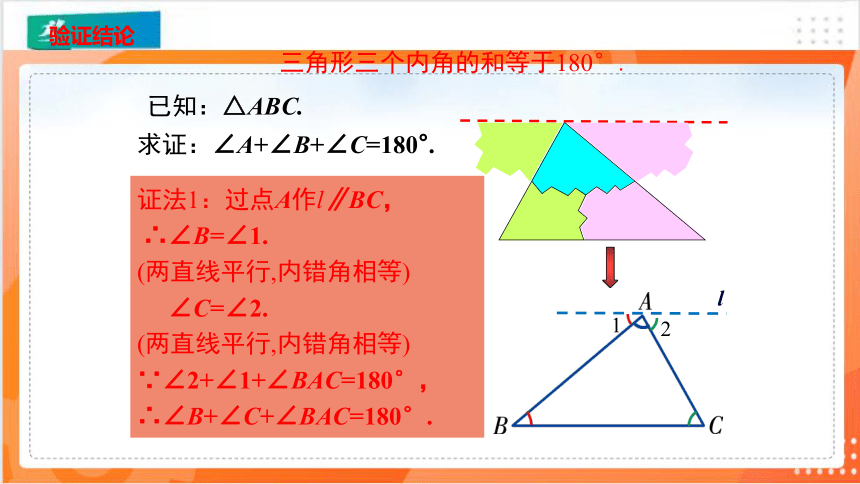
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
C
B
A
E
D
F
证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
想一想:同学们还有其他的方法吗?
思考:多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
例1 已知,如图,D是△ABC中BC边延长线上一点,F为AB上一点,直线FD交AC于E,∠DFB=90°,∠A=46°,∠D=50°.求∠ACB的度数.
解:在△DFB中,
∵∠DFB=90°,∠D=50°,
∠DFB+∠D+∠B=180°,
∴∠B=40°.
在△ABC中,
∵∠A=46°,∠B=40°,
∴∠ACB=180°-∠A-∠B=94°.
典例精析
同学们手中有直角三角板,请再画一个内角都不是90°的三角形.
三、三角形的按角的分类
探究新知
三个角都是锐角的三角形叫作锐角三角形;
锐角三角形
有一个角是钝角的三角形叫作钝角三角形.
钝角三角形
有一个角是直角的三角形叫作直角三角形;
直角三角形
直角边
直角边
斜边
A
B
C
直角三角形ABC可以写成Rt△ABC;
直角三角形
锐角三角形
钝角三角形
三角形
三角形按角的大小分类
根据“三角形的内角和为180°”易得“直角三角形的两个锐角互余”.
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
你能找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
四、三角形的按边的分类
探究新知
三条边各不相等的三角形叫作不等边三角形 ;
有两条边相等的三角形叫作等腰三角形;
三条边都相等的三角形叫作等边三角形.
等边三角形和等腰三角形之间有什么关系?
总结归纳
三角形按边分类
不等边三角形
等腰三角形
我们可以把三角形按照三边情况进行分类
腰和底不等的等腰三角形
等边三角形(三边都相等
的三角形)
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
小明家
五、三角形的三边关系
探究新知
A
B
C
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
请问:路线1、路线2哪条路程较短,你能说出根据吗?
解:路线2较短;两点之间线段最短.
由此可以得到:
归纳总结
三角形两边的和大于第三边.
三角形两边的差小于第三边.
议一议
1.在同一个三角形中,任意两边之和与第三边有什么
大小关系
2.在同一个三角形中,任意两边之差与第三边有什么
大小关系
3.三角形三边有怎样的不等关系
通过动手实验同学们可以得到哪些结论 理由是什么?
例1 有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
归纳
典例精析
例2 一个三角形的三边长分别为4,7,x,那么
x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
判断三角形边的取值范围要同时运用两边
之和大于第三边,两边之差小于第三边.
归纳
解析:∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11.
A
例3 若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和
大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
根据两边之和大于第三边,两边之差小于第三边,来判定绝对值里的式子的正负.
注意
(2)等边三角形是特殊的等腰三角形.( )
(1)一个钝角三角形一定不是等腰三角形.( )
(3)等腰三角形的腰和底一定不相等.( )
(5)直角三角形一定不是等腰三角形.( )
判断:
√
×
×
(4)等边三角形是锐角三角形.( )
×
√
练一练
1.已知∠A,∠B,∠C 是△ABC的三个内角,
∠A= 70°,∠C=30°,∠B =______.
2.直角三角形一个锐角为70°,另一个锐角
为_____.
80°
20°
课堂练习
3.在△ABC 中,∠A = 80°,∠B = ∠C,
则∠C=_______.
50°
4.如果△ABC 中∠A∶∠B∶∠C = 2∶3∶5,
此三角形按角分类应为____________.
直角三角形
5.三条线段的长度分别为:
B
(1)3cm,4cm,5cm;
(2)8cm,7cm,15cm;
(3)13cm,12cm,20cm;(4)5cm,5cm,11cm.
能组成三角形的有( )组.
A.1 B.2 C.3 D.4
6.现有长度分别为1cm,2cm,3cm,4cm,5cm 的五条线段,从其中选三条线段为边可以构成_____个的不同的三角形.
3
7.如果三角形的两边长分别是 2 和 4,且第三边是奇数,那么第三边长为______. 若第三边为偶数,那么三角形的周长______.
3或5
10
8.已知等腰三角形的两边长分别为4、9,求它的周长.
解:因为三角形是等腰三角形,
所以,当腰长为4时,
三角形的三边分别为:4、4、9,而4+4<9,
所以不能构成一个三角形,应舍去.
当腰长为9时,
三角形的三边分别为:9、9、4,4+9>9,
所以能构成一个三角形.
即周长为22.
三角形三个内角的和等于180°.
三角形按角的大小分类:
锐角三角形 :三个内角都是锐角.
直角三角形的两个锐角互余.
直角三角形 :有一个内角为直角.
钝角三角形 :有一个内角为钝角.
课堂小结
三角形中边的关系
三角形按边分类
不等边三角形
等腰三角形(包括等边三角形)
三角形的三边关系
任意两边之和大于第三边
任意两边之差小于第三边
https://www.21cnjy.com/help/help_extract.php
4.1.1 认识三角形
北师大版七年级下册数学
第四章 三角形
在我们日常生活中经常能看到三角形的影子.
减速慢行
注意儿童
前方村庄
情景引入
观察下面的屋顶框架图:
(1)你能从图中找出四个不同的三角形吗?
(2)这些三角形有什么共同的特点?
问题1:观察下面三角形的形成过程,说一说什么叫三角形
定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫作三角形.
问题2:三角形中有几条线段 有几个角
A
B
C
边:线段AB,BC,CA是三角形的边.
顶点:点A,B,C是三角形的顶点,
角:∠A,∠B,∠C叫作三角形的内角,简称三角
形的角.
有三条线段,三个角
一、三角形的概念
探究新知
记法:三角形ABC用符号表示________.
边的表示:三角形ABC的边AB、AC和BC可用小写字母分别表示为________.
△ABC
c,a,b
边c
边b
边a
顶点C
角
角
角
顶点A
顶点B
辨一辨:下列图形符合三角形的定义吗?
不符合
不符合
不符合
①位置关系:不在同一直线上;
②联接方式:首尾顺次相接.
三角形应满足以下两个条件:
要点提醒
表示方法:
三角形用符号“△”表示;记作“△ABC”,读作“三角形ABC”,除此△ABC还可记作△BCA,
△ CAB, △ ACB等.
基本要素:
三角形的边:边AB、BC、CA;
三角形的顶点:顶点A、B、C;
三角形的内角(简称为三角形的角):∠ A、 ∠ B、 ∠ C.
特别规定:
三角形ABC的三边,一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c.
5个,它们分别是△ABE,△ABC, △BEC,△BCD,△ECD.
找一找:(1)图中有几个三角形?用符号表示出这些三角形?
A
B
C
D
E
(2)以AB为边的三角形有哪些?
△ABC、△ABE.
(3)以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △CDE.
(4)以∠D为角的三角形有哪些?
△ BCD、 △DEC.
(5)说出△BCD的三个角和三个顶点所对的边.
△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.
A
B
C
D
E
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
还有其他的拼接方法吗?
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
二、三角形的内角和
探究新知
验证结论
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
C
B
A
E
D
F
证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
想一想:同学们还有其他的方法吗?
思考:多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
例1 已知,如图,D是△ABC中BC边延长线上一点,F为AB上一点,直线FD交AC于E,∠DFB=90°,∠A=46°,∠D=50°.求∠ACB的度数.
解:在△DFB中,
∵∠DFB=90°,∠D=50°,
∠DFB+∠D+∠B=180°,
∴∠B=40°.
在△ABC中,
∵∠A=46°,∠B=40°,
∴∠ACB=180°-∠A-∠B=94°.
典例精析
同学们手中有直角三角板,请再画一个内角都不是90°的三角形.
三、三角形的按角的分类
探究新知
三个角都是锐角的三角形叫作锐角三角形;
锐角三角形
有一个角是钝角的三角形叫作钝角三角形.
钝角三角形
有一个角是直角的三角形叫作直角三角形;
直角三角形
直角边
直角边
斜边
A
B
C
直角三角形ABC可以写成Rt△ABC;
直角三角形
锐角三角形
钝角三角形
三角形
三角形按角的大小分类
根据“三角形的内角和为180°”易得“直角三角形的两个锐角互余”.
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
你能找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
四、三角形的按边的分类
探究新知
三条边各不相等的三角形叫作不等边三角形 ;
有两条边相等的三角形叫作等腰三角形;
三条边都相等的三角形叫作等边三角形.
等边三角形和等腰三角形之间有什么关系?
总结归纳
三角形按边分类
不等边三角形
等腰三角形
我们可以把三角形按照三边情况进行分类
腰和底不等的等腰三角形
等边三角形(三边都相等
的三角形)
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
小明家
五、三角形的三边关系
探究新知
A
B
C
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
请问:路线1、路线2哪条路程较短,你能说出根据吗?
解:路线2较短;两点之间线段最短.
由此可以得到:
归纳总结
三角形两边的和大于第三边.
三角形两边的差小于第三边.
议一议
1.在同一个三角形中,任意两边之和与第三边有什么
大小关系
2.在同一个三角形中,任意两边之差与第三边有什么
大小关系
3.三角形三边有怎样的不等关系
通过动手实验同学们可以得到哪些结论 理由是什么?
例1 有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
归纳
典例精析
例2 一个三角形的三边长分别为4,7,x,那么
x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
判断三角形边的取值范围要同时运用两边
之和大于第三边,两边之差小于第三边.
归纳
解析:∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11.
A
例3 若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和
大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
根据两边之和大于第三边,两边之差小于第三边,来判定绝对值里的式子的正负.
注意
(2)等边三角形是特殊的等腰三角形.( )
(1)一个钝角三角形一定不是等腰三角形.( )
(3)等腰三角形的腰和底一定不相等.( )
(5)直角三角形一定不是等腰三角形.( )
判断:
√
×
×
(4)等边三角形是锐角三角形.( )
×
√
练一练
1.已知∠A,∠B,∠C 是△ABC的三个内角,
∠A= 70°,∠C=30°,∠B =______.
2.直角三角形一个锐角为70°,另一个锐角
为_____.
80°
20°
课堂练习
3.在△ABC 中,∠A = 80°,∠B = ∠C,
则∠C=_______.
50°
4.如果△ABC 中∠A∶∠B∶∠C = 2∶3∶5,
此三角形按角分类应为____________.
直角三角形
5.三条线段的长度分别为:
B
(1)3cm,4cm,5cm;
(2)8cm,7cm,15cm;
(3)13cm,12cm,20cm;(4)5cm,5cm,11cm.
能组成三角形的有( )组.
A.1 B.2 C.3 D.4
6.现有长度分别为1cm,2cm,3cm,4cm,5cm 的五条线段,从其中选三条线段为边可以构成_____个的不同的三角形.
3
7.如果三角形的两边长分别是 2 和 4,且第三边是奇数,那么第三边长为______. 若第三边为偶数,那么三角形的周长______.
3或5
10
8.已知等腰三角形的两边长分别为4、9,求它的周长.
解:因为三角形是等腰三角形,
所以,当腰长为4时,
三角形的三边分别为:4、4、9,而4+4<9,
所以不能构成一个三角形,应舍去.
当腰长为9时,
三角形的三边分别为:9、9、4,4+9>9,
所以能构成一个三角形.
即周长为22.
三角形三个内角的和等于180°.
三角形按角的大小分类:
锐角三角形 :三个内角都是锐角.
直角三角形的两个锐角互余.
直角三角形 :有一个内角为直角.
钝角三角形 :有一个内角为钝角.
课堂小结
三角形中边的关系
三角形按边分类
不等边三角形
等腰三角形(包括等边三角形)
三角形的三边关系
任意两边之和大于第三边
任意两边之差小于第三边
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
