沪科版九年级数学下24.3圆周角 (第1课时 圆周角及其推论)课件(共22张PPT)
文档属性
| 名称 | 沪科版九年级数学下24.3圆周角 (第1课时 圆周角及其推论)课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 287.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 09:44:05 | ||
图片预览




文档简介
(共22张PPT)
24.3 圆 周 角
第24章 圆
沪科版九年级数学下
第1课时 圆周角及其推论
旧知复习
1.什么叫圆心角
.
O
A
B
顶点在圆心的角叫圆心角
2. 圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
新知探究
.
O
A
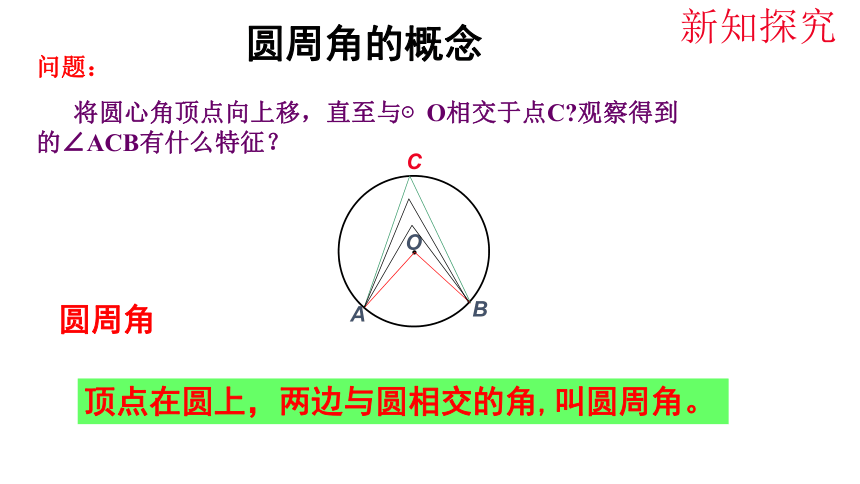
问题:
将圆心角顶点向上移,直至与⊙O相交于点C 观察得到的∠ACB有什么特征?
C
B
圆周角的概念
顶点在圆上,两边与圆相交的角,叫圆周角。
圆周角
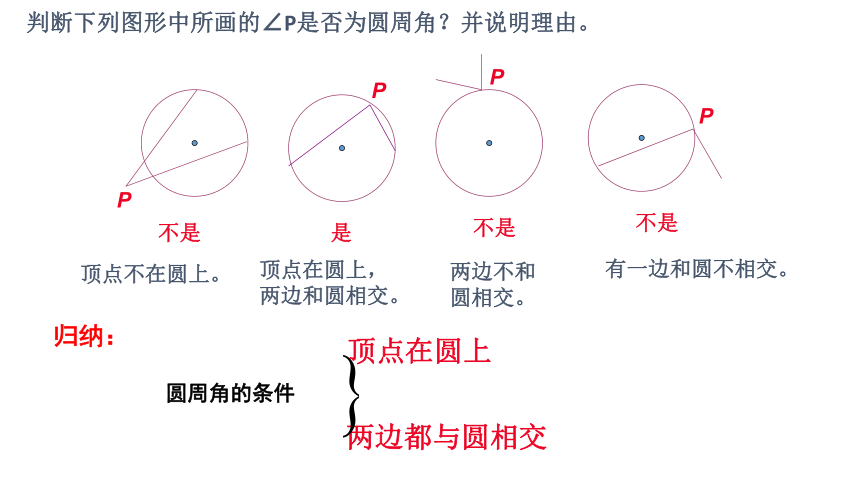
判断下列图形中所画的∠P是否为圆周角?并说明理由。
P
P
P
P
不是
是
不是
不是
顶点不在圆上。
顶点在圆上,两边和圆相交。
两边不和圆相交。
有一边和圆不相交。
归纳:
圆周角的条件
顶点在圆上
两边都与圆相交
C
B
A
O
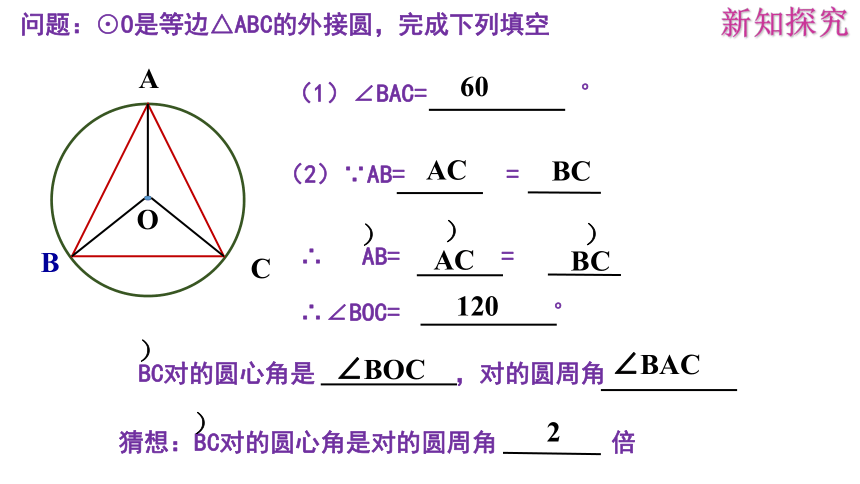
问题:⊙O是等边△ABC的外接圆,完成下列填空
新知探究
(1)∠BAC= °
∴∠BOC= °
(2)∵AB= =
∴ AB= =
)
)
)
BC对的圆心角是 ,对的圆周角
)
猜想:BC对的圆心角是对的圆周角 倍
)
60
AC
BC
AC
BC
120
∠BOC
∠BAC
2
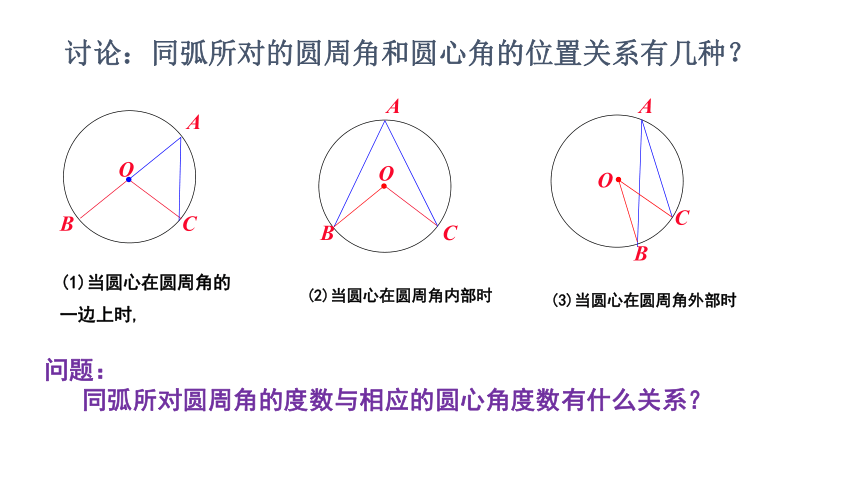
讨论:同弧所对的圆周角和圆心角的位置关系有几种?
A
B
C
O
A
B
C
O
A
B
C
O
问题:
同弧所对圆周角的度数与相应的圆心角度数有什么关系?
(1)当圆心在圆周角的一边上时,
(2)当圆心在圆周角内部时
(3)当圆心在圆周角外部时
问题:
同弧所对圆周角的度数与相应的圆心角度数有什么关系?
(1)当圆心在圆周角的一边上时,
新知探究
证明:(圆心在圆周角上)
结论:在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半.
C
O
B
A
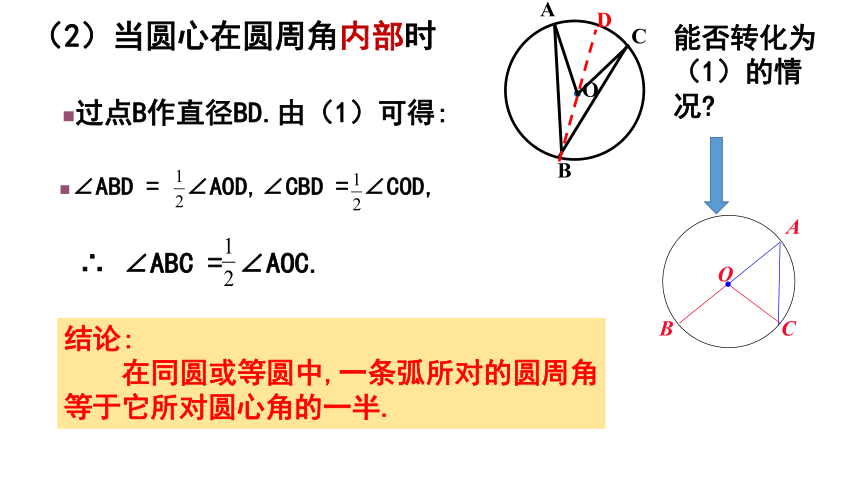
(2)当圆心在圆周角内部时
能否转化为(1)的情况
过点B作直径BD.由(1)可得:
∴ ∠ABC = ∠AOC.
∠ABD = ∠AOD,∠CBD = ∠COD,
●O
A
B
C
D
结论:
在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半.
A
B
C
O
(3)当圆心在圆周角外部时
结论:
在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半.
转化为(1)的情况
过点B作直径BD.由(1)可得:
∴ ∠ABC = ∠AOC.
∠ABD = ∠AOD,∠CBD = ∠COD,
●O
D
A
B
C
A
B
C
O
一弧所对的圆周角度数等于这条弧所对的圆心角的一半
A
B
C
O
A
B
C
O
A
B
C
O
即∠BAC= ∠BOC
圆周角定理:
综上所述我们得到:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
例1、已知:△ABC的三个顶点在上,∠BAC=50°,∠ABC=47°,求∠AOB.
解:有题意知:∠A、∠B、∠C是圆周角,
∠AOB是圆心角.
又∵∠BAC=50°,∠ABC=47° ∴∠ACB=180°-(∠A+∠B)
=180°-(50°+47°)
=83°.
∴ ∠AOB=2∠ACB=2×83°=166°.
B
A
C
O
例题精讲
A
B
C
O
已知: ⊙O的弦AB长等于圆的半径,求该弦所对的圆心角和圆周角的度数,
O
A
B
C
随堂练习1
A
B
O
图2
问题1:
如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系 为什么
∠B = ∠D= ∠E
●O
B
A
C
D
E
图1
∠C =∠G
新知再探
问题2.如图2,在⊙O中,若AB等于弧EF.能否得到∠C =∠G呢?
)
)
问题3.如图2,在⊙O中,若∠C =∠G,AB与EF相等吗.
)
)
)
)
AB
EF
=
推论1:在同圆或等圆中,同弧或等弧所对的两个圆周角相等,相等的圆周角所对的弧也相等
●O
B
A
C
D
E
圆周角定理推论
B
B′
A
C
C′
O
O
A
B
C
2. 90°的圆周角所对的弦是否是直径?
思考:
推论2:
半圆或直径所对的圆周角都相等,都等于90°(直角).反过来也是成立的,即90°的圆周角所对的弦是圆的直径
90°
1.半圆或直径所对的圆周角等于多少度?
∵ AB是直径
∴ ∠ACB=900
∵ ∠ACB=900
∴ AB是直径
AB是直径
总结
1、圆周角定理的推论1:
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
2、圆周角定理的推论2:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
用于找相等的角
用于找相等的弧
用于判断某个圆周角是否是直角
用于判断某条线是否过圆心
练一练. 试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠2=∠7
∠1=∠4
∠3=∠6
∠5=∠8
B
A
C
D
E
F
G
O
例2、 在⊙O中,AB是直径, 弦CG⊥AB于D,交BF于E,求证:BE=EC
︵
︵
CB
CF
=
例题精讲
证明:
连结CB
︵
︵
∵CB
CF
=
∵AB是直径, CG⊥AB于D
︵
︵
∴CB
BG
=
︵
︵
∴BG
CF
=
∴∠FBG=∠GCB
∴BE=CE
·
·
A
P
B
C
O
∴∠ABC=∠APC=60°
∴∠BAC=∠CPB=60°。
∴△ABC等边三角形。
.例3:如图,P是圆上的一点∠APC=∠CPB=60°,
求证:△ABC是等边三角形
证明:∵∠ABC和∠APC都是 所对的圆周角。
AC
⌒
∵∠BAC和∠CPB都是
所对的圆周角,
BC
⌒
例题精讲
1. 如图,等边三角形ABC,点D是⊙O上一点,则∠BDC = ;
60°
2.如图,在⊙O中,AB是⊙O的直径,∠D=20°,则∠AOC的度数为_____
140°
A
B
D
C
O
3.如图,AB和CD都是⊙0的直径,∠AOC=60°,则∠C的度数是 。
30°
随堂练习2:
5.如图,∠C是⊙O的圆周角,∠C=38°,则∠OAB= .
C
B
A
O
4、如图,AB是⊙O的直径,点C在圆上,∠A=20°,则∠B= 度
6.如图,在⊙O中,∠AOD=120 ,∠BDP=25 ,则∠P的度数等于 。
70°
52°
35°
7、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.
A
B
O
C
D
40°
50°
8. 在⊙O中,弦AB所对的圆心∠AOB=100°,则弦AB所对的圆周角为____________.
500或1300
A
B
O
C
D
24.3 圆 周 角
第24章 圆
沪科版九年级数学下
第1课时 圆周角及其推论
旧知复习
1.什么叫圆心角
.
O
A
B
顶点在圆心的角叫圆心角
2. 圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
新知探究
.
O
A
问题:
将圆心角顶点向上移,直至与⊙O相交于点C 观察得到的∠ACB有什么特征?
C
B
圆周角的概念
顶点在圆上,两边与圆相交的角,叫圆周角。
圆周角
判断下列图形中所画的∠P是否为圆周角?并说明理由。
P
P
P
P
不是
是
不是
不是
顶点不在圆上。
顶点在圆上,两边和圆相交。
两边不和圆相交。
有一边和圆不相交。
归纳:
圆周角的条件
顶点在圆上
两边都与圆相交
C
B
A
O
问题:⊙O是等边△ABC的外接圆,完成下列填空
新知探究
(1)∠BAC= °
∴∠BOC= °
(2)∵AB= =
∴ AB= =
)
)
)
BC对的圆心角是 ,对的圆周角
)
猜想:BC对的圆心角是对的圆周角 倍
)
60
AC
BC
AC
BC
120
∠BOC
∠BAC
2
讨论:同弧所对的圆周角和圆心角的位置关系有几种?
A
B
C
O
A
B
C
O
A
B
C
O
问题:
同弧所对圆周角的度数与相应的圆心角度数有什么关系?
(1)当圆心在圆周角的一边上时,
(2)当圆心在圆周角内部时
(3)当圆心在圆周角外部时
问题:
同弧所对圆周角的度数与相应的圆心角度数有什么关系?
(1)当圆心在圆周角的一边上时,
新知探究
证明:(圆心在圆周角上)
结论:在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半.
C
O
B
A
(2)当圆心在圆周角内部时
能否转化为(1)的情况
过点B作直径BD.由(1)可得:
∴ ∠ABC = ∠AOC.
∠ABD = ∠AOD,∠CBD = ∠COD,
●O
A
B
C
D
结论:
在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半.
A
B
C
O
(3)当圆心在圆周角外部时
结论:
在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半.
转化为(1)的情况
过点B作直径BD.由(1)可得:
∴ ∠ABC = ∠AOC.
∠ABD = ∠AOD,∠CBD = ∠COD,
●O
D
A
B
C
A
B
C
O
一弧所对的圆周角度数等于这条弧所对的圆心角的一半
A
B
C
O
A
B
C
O
A
B
C
O
即∠BAC= ∠BOC
圆周角定理:
综上所述我们得到:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
例1、已知:△ABC的三个顶点在上,∠BAC=50°,∠ABC=47°,求∠AOB.
解:有题意知:∠A、∠B、∠C是圆周角,
∠AOB是圆心角.
又∵∠BAC=50°,∠ABC=47° ∴∠ACB=180°-(∠A+∠B)
=180°-(50°+47°)
=83°.
∴ ∠AOB=2∠ACB=2×83°=166°.
B
A
C
O
例题精讲
A
B
C
O
已知: ⊙O的弦AB长等于圆的半径,求该弦所对的圆心角和圆周角的度数,
O
A
B
C
随堂练习1
A
B
O
图2
问题1:
如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系 为什么
∠B = ∠D= ∠E
●O
B
A
C
D
E
图1
∠C =∠G
新知再探
问题2.如图2,在⊙O中,若AB等于弧EF.能否得到∠C =∠G呢?
)
)
问题3.如图2,在⊙O中,若∠C =∠G,AB与EF相等吗.
)
)
)
)
AB
EF
=
推论1:在同圆或等圆中,同弧或等弧所对的两个圆周角相等,相等的圆周角所对的弧也相等
●O
B
A
C
D
E
圆周角定理推论
B
B′
A
C
C′
O
O
A
B
C
2. 90°的圆周角所对的弦是否是直径?
思考:
推论2:
半圆或直径所对的圆周角都相等,都等于90°(直角).反过来也是成立的,即90°的圆周角所对的弦是圆的直径
90°
1.半圆或直径所对的圆周角等于多少度?
∵ AB是直径
∴ ∠ACB=900
∵ ∠ACB=900
∴ AB是直径
AB是直径
总结
1、圆周角定理的推论1:
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
2、圆周角定理的推论2:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
用于找相等的角
用于找相等的弧
用于判断某个圆周角是否是直角
用于判断某条线是否过圆心
练一练. 试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠2=∠7
∠1=∠4
∠3=∠6
∠5=∠8
B
A
C
D
E
F
G
O
例2、 在⊙O中,AB是直径, 弦CG⊥AB于D,交BF于E,求证:BE=EC
︵
︵
CB
CF
=
例题精讲
证明:
连结CB
︵
︵
∵CB
CF
=
∵AB是直径, CG⊥AB于D
︵
︵
∴CB
BG
=
︵
︵
∴BG
CF
=
∴∠FBG=∠GCB
∴BE=CE
·
·
A
P
B
C
O
∴∠ABC=∠APC=60°
∴∠BAC=∠CPB=60°。
∴△ABC等边三角形。
.例3:如图,P是圆上的一点∠APC=∠CPB=60°,
求证:△ABC是等边三角形
证明:∵∠ABC和∠APC都是 所对的圆周角。
AC
⌒
∵∠BAC和∠CPB都是
所对的圆周角,
BC
⌒
例题精讲
1. 如图,等边三角形ABC,点D是⊙O上一点,则∠BDC = ;
60°
2.如图,在⊙O中,AB是⊙O的直径,∠D=20°,则∠AOC的度数为_____
140°
A
B
D
C
O
3.如图,AB和CD都是⊙0的直径,∠AOC=60°,则∠C的度数是 。
30°
随堂练习2:
5.如图,∠C是⊙O的圆周角,∠C=38°,则∠OAB= .
C
B
A
O
4、如图,AB是⊙O的直径,点C在圆上,∠A=20°,则∠B= 度
6.如图,在⊙O中,∠AOD=120 ,∠BDP=25 ,则∠P的度数等于 。
70°
52°
35°
7、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.
A
B
O
C
D
40°
50°
8. 在⊙O中,弦AB所对的圆心∠AOB=100°,则弦AB所对的圆周角为____________.
500或1300
A
B
O
C
D
