沪科版数学九年级下24.1.1 图形的旋转 课件(共65张PPT)
文档属性
| 名称 | 沪科版数学九年级下24.1.1 图形的旋转 课件(共65张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 00:00:00 | ||
图片预览







文档简介
(共65张PPT)
24.1 旋 转
第一课时 旋转的概念
沪科版九年级数学下
第24章 圆
一、引入:
生活中的圆到处可见,请同学们欣赏下面几幅图片。
从本章起,我们来学习圆的有关知识,本节课
首先来学习旋转。
四、合作探究:
旋转展示
1.旋转的概念
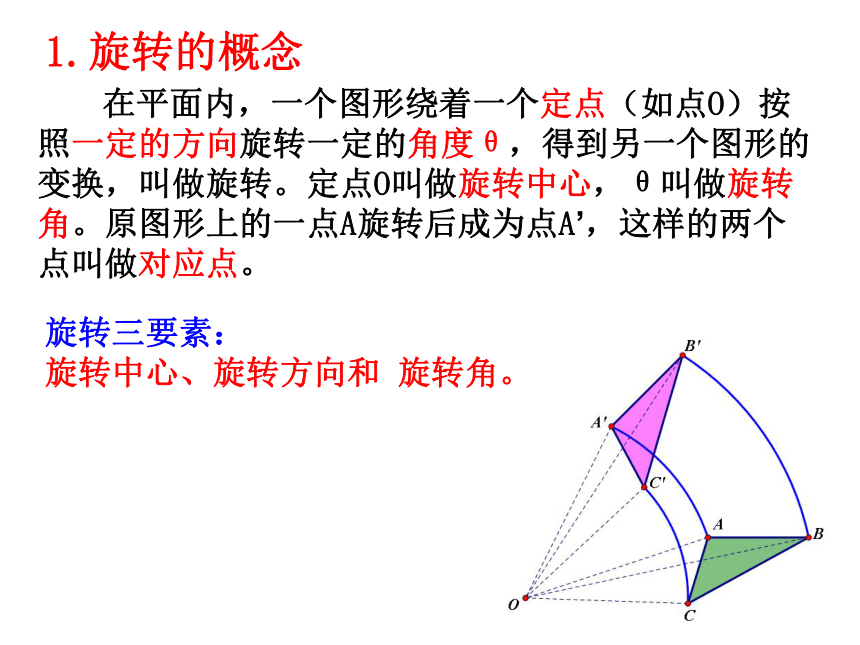
在平面内,一个图形绕着一个定点(如点O)按照一定的方向旋转一定的角度θ,得到另一个图形的变换,叫做旋转。定点O叫做旋转中心,θ叫做旋转角。原图形上的一点A旋转后成为点A’,这样的两个点叫做对应点。
旋转三要素:
旋转中心、旋转方向和 旋转角。
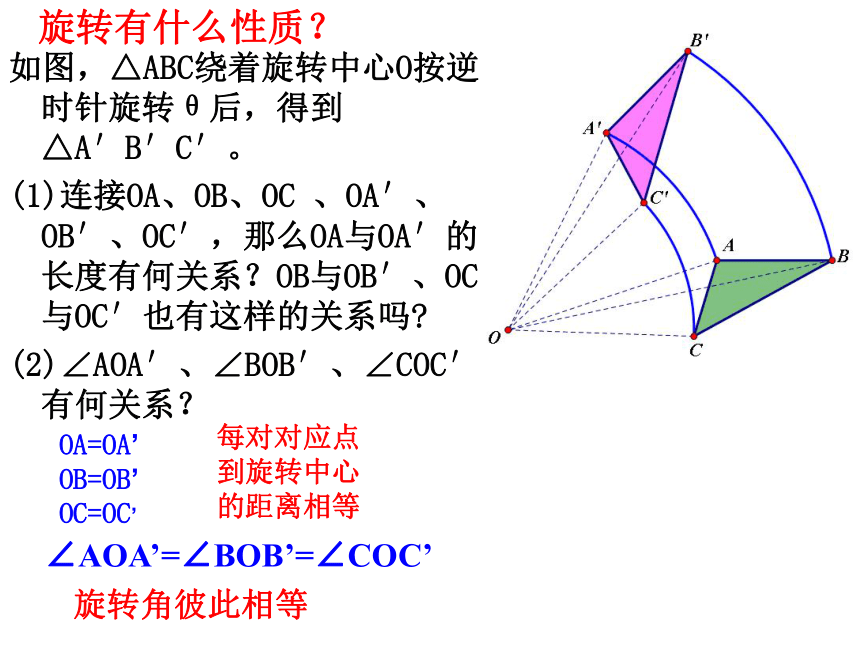
如图,△ABC绕着旋转中心O按逆时针旋转θ后,得到△A′B′C′。
(1)连接OA、OB、OC 、OA′、OB′、OC′,那么OA与OA′的长度有何关系?OB与OB′、OC与OC′也有这样的关系吗
(2)∠AOA′、∠BOB′、∠COC′有何关系?
OA=OA’
OB=OB’
OC=OC’
每对对应点到旋转中心的距离相等
∠AOA’=∠BOB’=∠COC’
旋转角彼此相等
旋转有什么性质?
2.旋转的性质:
一个图形和它经过旋转所得到的图形中,
(1)对应点到旋转中心的距离相等;
(2)两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
(3)旋转中心是唯一不动的点。
(4)旋转前后的两个图形是全等形。
电风扇叶
紫金花
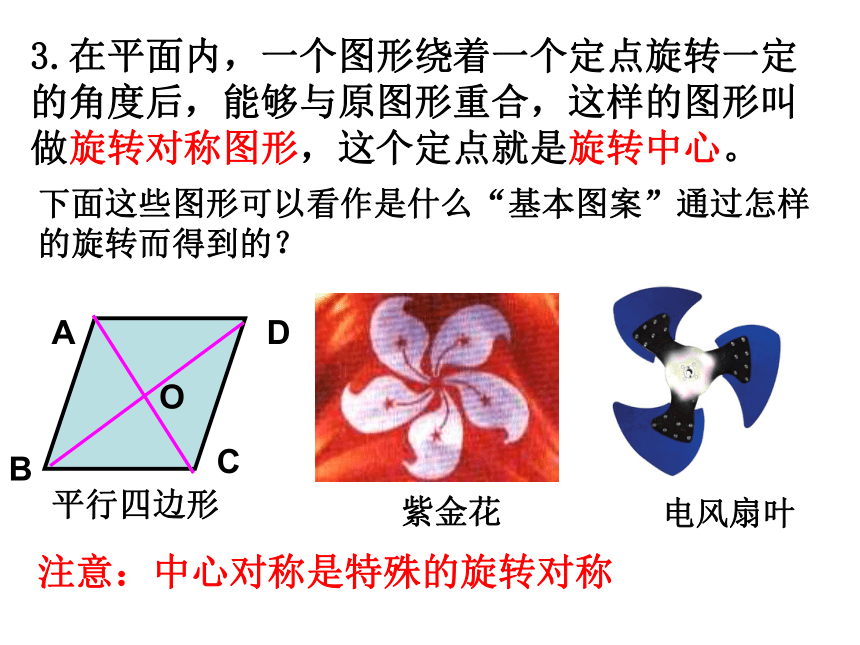
下面这些图形可以看作是什么“基本图案”通过怎样的旋转而得到的?
平行四边形
A
B
C
D
O
3.在平面内,一个图形绕着一个定点旋转一定的角度后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心。
注意:中心对称是特殊的旋转对称
1.如图,如果把钟表的指针看做△OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移动到什么位置?
理解应用:
2.如图,四边形ABCD、四边形EFGH都是边长为1的正方形.
(1)这个图案可以看做是哪个“基本图案”通过旋转得到的?
(2)请画出旋转中心和旋转角。
(3)指出,经过旋转,点A、B、C、D分别移到什么位置?
理解应用:
O
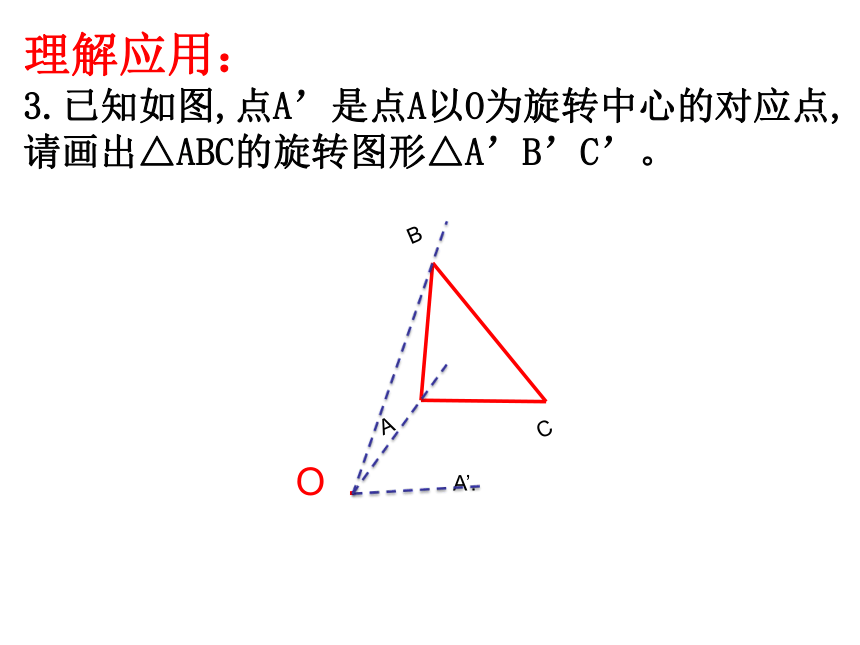
3.已知如图,点A’是点A以O为旋转中心的对应点,请画出△ABC的旋转图形△A’B’C’。
B
A
C
O .
A’.
理解应用:
7.利用平移,轴对称,旋转可以将一个图形作一种或几种变换,可以进行图案设计。
平移
轴对称
中心对称(旋转180度)
先轴对称,再旋转180度
24.1 旋 转
2.如图所示,P是等边 ABC内的一点,把 ABP按不同的
方向通过旋转得到 BQC和 ACR。
指出旋转中心、旋转方向和旋转角度?
A
B
C
P
Q
R
复习回顾
(1)把其中一个图案绕点O旋转180°,你有什么发现
观察
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
A
B
C
D
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
A
B
C
D
O
探究
1.中心对称:
把一个图形绕着某一点旋转180°,如果它能够与另一个图象重合,那么就说这两个图象关于这个点对称或中心对称。这个点叫
做对称中心,这两个图形中的对应点叫做关于中心的对称点。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
总结新知
中心对称与轴对称区别与联系
轴对称 中心对称
有一条对称轴---直线 有一个对称中心---点
图形沿对称轴对折(翻折1800)后重合 图形绕对称中心旋转1800后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
请你动手:将一个三角板放在纸上,画出△ABC,再将三角板绕一个顶点旋转180o,画出△A’B’C’,移开三角板,画出的△ABC与△A’B’C’关于点O对称。分别连接对称点AA’ 、BB’、CC’,点O在线段AA’上吗?如果在,在什么位置? △ABC与 △A’B’C’有什么关系?
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
分别连接对称点AA’ 、BB’、CC’,点O在线段AA’上吗?如果在,在什么位置? △ABC与 △A’B’C’有什么关系?
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
D
F
E
2.中心对称的性质:
(1)中心对称的两个图形,对称点的连线段都经过对称中心,并且被对称中心所平分;
(2)中心对称的两个图形是全等图形。
如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
中心对称判定
归纳:
A
O
A'
连结OA,
并延长到A’,使OA’=OA,
例1、已知A点和O点,画出点A关于点O的对称点A'
则A’是所求的点
例2、已知线段AB和O点,画出线段AB关于点O的
对称线段A’B’
O
A'
B'
A
B
连结AO并延长到A’,使OA’=OA,
则得A的对称点A’
连结BO并延长到B’,使OB’=OB,
则得B的对称点B’
连结A’B’,则线段A’B’是所画线段
例题讲解
A
A′
B′
B
O
2、线段的中心对称线段的作法
A
O
A′
1、点的中心对称点的作法
中心对称作图
以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
线段A′B′就是所求的线段
点A′即为所求的点
如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
解:
A′
C′
B′
△A′B′C′即为所求的三角形。
练习
例2、已知四边形ABCD和点O(下图),画四边形A’B’C’D’,使它与已知四边形关于点O对称.
.
o
A
B
C
D
A’
B’
C’
D’
画法:1. 连结AO并延长到A’,使
OA’=OA,得到点A的对称点A’.
2. 同样画B、C、D的对称点 B’、C’、D’.
3. 顺次连结A’、B’、C’、D’各点.
四边形A’B’C’D’就是所求的四边形.
练习:画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。
D
A
B
C
E
F
G
M
D
A
B
C
O
.
N
A
B
C
D
F
E
O
例3.如图,点O是平行四边形的对称中心,点A、C关于点O对称,有AO=CO,那么OE=OF吗?
对称中心平分连结两个对称点的线段.
EF经过点O,分别交AB、CD于E、F。
解:∵平行四边形是中心对称图形,O是对称中心.
∴点E、F是关于点O的对称点。
∴OE=OF。
A
B
C
D
F
E
O
例题讲解
巩固练习:如图23.2-5,选择点O为对称中心,画出与△ABC关于点O对称的△A’B’C’.
能力提高 : 已知四边形ABCD,画四边形A’B’C’D’,使它与已知四边形关于点A对称。
解:
A
B
C
D
24.1旋转
第三课时 中心对称图形
观察:下列图形,绕中心点旋转多少度能与自身重合?它们的旋转角度有什么相同点?
(1) 这些图形有什么共同的特征?
(2)这些图形都可以绕某个点旋转哪个角度后与原来的图形重合
在平面内,一个图形绕某个点旋转180o,能与自身重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
特征:(1)中心对称图形绕着它的中心点旋转180°后与自身重合;(2)中心对称图形也是一种特殊的旋转对称图形。
O
B
A
C
D
对称中心是 ______,
点O
点A的对称点是 ______,
点D的对称点是 ______,
点C
点B
平行四边形ABCD绕点O旋转180°后,能与本身重合。
这一类图形本身关于某点成中心对称。
名称 中心对称 中心对称图形
定义
性质
区别
联系
中心对称与中心对称图形的区别与联系
把一个图形绕着某一个点旋转180 ,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称,这两个图形中的对应点叫做关于中心的对称点
如果一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心
①两个图形完全重合;
②对应点连线都经过对称中心,并且被对称中心平分
________
①两个图形的关系
②对称点在两个图形上
①具有某种性质的一个图形
②对称点在一个图形上
若把中心对称图形的两部分分别看作两图,则它们成中心对称。若把中心对称的两图看作一个整体,则成为中心对称图形。
下列图形是中心对称图形吗?
小练习
认真观察旋转180°后……
都是中心对称图形。
图形的中心就是对称中心。
都是中心对称图形。
图形的中心就是对称中心。
线段、三角形、平行四边形、长方形、正方形、圆是中心对称图形吗?如果是,那么对称中心又在哪里?
1. 选择题:
(1)下列图形中即是轴对称图形又是中心对称图形的是( )
A. 角 B. 等边三角形 C. 线段 D. 平行四边形
C
(2)下列多边形中,是中心对称图形而不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
A
随堂练习
2. 判断下列说法是否正确。
(1)轴对称图形也是中心对称图形。( )
(2)旋转对称图形也是中心对称图形。( )
(3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( )
(4)角是轴对称图形也是中心对称图形。( )
(5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等。 ( )
×
√
×
√
×
3. 判断下列图形是否是中心对称图形
√
×
√
√
√
√
√
√
√
×
√
×
√
√
×
√
×
√
√
√
√
√
√
4. 观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
(1)
(3)
(2)
(4)
(5)
(6)
(3)(4)(6)
(1)
(2)(5)
5. 在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有______________
_______,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________.
①⑤⑥⑦⑧⑨
①②③④
①⑥⑦⑧⑨
⑥⑦⑧⑨
旋转前后的图形完全重合
轴对称图形
中心对称图形
有一条对称轴
——
直线
有一个对称中心
——
点
图形沿轴对折(翻转
180°
)
图形绕对称中心旋转
180°
翻转前后的图形完全重合
中心对称图形与轴对称图形的区别与联系
课堂小结
24.1 旋 转
第一课时 旋转的概念
沪科版九年级数学下
第24章 圆
一、引入:
生活中的圆到处可见,请同学们欣赏下面几幅图片。
从本章起,我们来学习圆的有关知识,本节课
首先来学习旋转。
四、合作探究:
旋转展示
1.旋转的概念
在平面内,一个图形绕着一个定点(如点O)按照一定的方向旋转一定的角度θ,得到另一个图形的变换,叫做旋转。定点O叫做旋转中心,θ叫做旋转角。原图形上的一点A旋转后成为点A’,这样的两个点叫做对应点。
旋转三要素:
旋转中心、旋转方向和 旋转角。
如图,△ABC绕着旋转中心O按逆时针旋转θ后,得到△A′B′C′。
(1)连接OA、OB、OC 、OA′、OB′、OC′,那么OA与OA′的长度有何关系?OB与OB′、OC与OC′也有这样的关系吗
(2)∠AOA′、∠BOB′、∠COC′有何关系?
OA=OA’
OB=OB’
OC=OC’
每对对应点到旋转中心的距离相等
∠AOA’=∠BOB’=∠COC’
旋转角彼此相等
旋转有什么性质?
2.旋转的性质:
一个图形和它经过旋转所得到的图形中,
(1)对应点到旋转中心的距离相等;
(2)两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
(3)旋转中心是唯一不动的点。
(4)旋转前后的两个图形是全等形。
电风扇叶
紫金花
下面这些图形可以看作是什么“基本图案”通过怎样的旋转而得到的?
平行四边形
A
B
C
D
O
3.在平面内,一个图形绕着一个定点旋转一定的角度后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心。
注意:中心对称是特殊的旋转对称
1.如图,如果把钟表的指针看做△OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移动到什么位置?
理解应用:
2.如图,四边形ABCD、四边形EFGH都是边长为1的正方形.
(1)这个图案可以看做是哪个“基本图案”通过旋转得到的?
(2)请画出旋转中心和旋转角。
(3)指出,经过旋转,点A、B、C、D分别移到什么位置?
理解应用:
O
3.已知如图,点A’是点A以O为旋转中心的对应点,请画出△ABC的旋转图形△A’B’C’。
B
A
C
O .
A’.
理解应用:
7.利用平移,轴对称,旋转可以将一个图形作一种或几种变换,可以进行图案设计。
平移
轴对称
中心对称(旋转180度)
先轴对称,再旋转180度
24.1 旋 转
2.如图所示,P是等边 ABC内的一点,把 ABP按不同的
方向通过旋转得到 BQC和 ACR。
指出旋转中心、旋转方向和旋转角度?
A
B
C
P
Q
R
复习回顾
(1)把其中一个图案绕点O旋转180°,你有什么发现
观察
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
A
B
C
D
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
探究
(1)如图所示,把其中一个图案绕点O旋转
180°,你有什么发现?
(2)如图所示,线段AC,BD相交于点O,OA=OC,OB=OD
把△OCD绕点O旋转180 °,你能发现什么?
O
A
B
C
D
O
探究
1.中心对称:
把一个图形绕着某一点旋转180°,如果它能够与另一个图象重合,那么就说这两个图象关于这个点对称或中心对称。这个点叫
做对称中心,这两个图形中的对应点叫做关于中心的对称点。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
总结新知
中心对称与轴对称区别与联系
轴对称 中心对称
有一条对称轴---直线 有一个对称中心---点
图形沿对称轴对折(翻折1800)后重合 图形绕对称中心旋转1800后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
请你动手:将一个三角板放在纸上,画出△ABC,再将三角板绕一个顶点旋转180o,画出△A’B’C’,移开三角板,画出的△ABC与△A’B’C’关于点O对称。分别连接对称点AA’ 、BB’、CC’,点O在线段AA’上吗?如果在,在什么位置? △ABC与 △A’B’C’有什么关系?
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
分别连接对称点AA’ 、BB’、CC’,点O在线段AA’上吗?如果在,在什么位置? △ABC与 △A’B’C’有什么关系?
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
探究:旋转三角尺,画出关于点O对称的两个三角形。
O
A
B
C
D
F
E
2.中心对称的性质:
(1)中心对称的两个图形,对称点的连线段都经过对称中心,并且被对称中心所平分;
(2)中心对称的两个图形是全等图形。
如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
中心对称判定
归纳:
A
O
A'
连结OA,
并延长到A’,使OA’=OA,
例1、已知A点和O点,画出点A关于点O的对称点A'
则A’是所求的点
例2、已知线段AB和O点,画出线段AB关于点O的
对称线段A’B’
O
A'
B'
A
B
连结AO并延长到A’,使OA’=OA,
则得A的对称点A’
连结BO并延长到B’,使OB’=OB,
则得B的对称点B’
连结A’B’,则线段A’B’是所画线段
例题讲解
A
A′
B′
B
O
2、线段的中心对称线段的作法
A
O
A′
1、点的中心对称点的作法
中心对称作图
以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
线段A′B′就是所求的线段
点A′即为所求的点
如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
解:
A′
C′
B′
△A′B′C′即为所求的三角形。
练习
例2、已知四边形ABCD和点O(下图),画四边形A’B’C’D’,使它与已知四边形关于点O对称.
.
o
A
B
C
D
A’
B’
C’
D’
画法:1. 连结AO并延长到A’,使
OA’=OA,得到点A的对称点A’.
2. 同样画B、C、D的对称点 B’、C’、D’.
3. 顺次连结A’、B’、C’、D’各点.
四边形A’B’C’D’就是所求的四边形.
练习:画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。
D
A
B
C
E
F
G
M
D
A
B
C
O
.
N
A
B
C
D
F
E
O
例3.如图,点O是平行四边形的对称中心,点A、C关于点O对称,有AO=CO,那么OE=OF吗?
对称中心平分连结两个对称点的线段.
EF经过点O,分别交AB、CD于E、F。
解:∵平行四边形是中心对称图形,O是对称中心.
∴点E、F是关于点O的对称点。
∴OE=OF。
A
B
C
D
F
E
O
例题讲解
巩固练习:如图23.2-5,选择点O为对称中心,画出与△ABC关于点O对称的△A’B’C’.
能力提高 : 已知四边形ABCD,画四边形A’B’C’D’,使它与已知四边形关于点A对称。
解:
A
B
C
D
24.1旋转
第三课时 中心对称图形
观察:下列图形,绕中心点旋转多少度能与自身重合?它们的旋转角度有什么相同点?
(1) 这些图形有什么共同的特征?
(2)这些图形都可以绕某个点旋转哪个角度后与原来的图形重合
在平面内,一个图形绕某个点旋转180o,能与自身重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
特征:(1)中心对称图形绕着它的中心点旋转180°后与自身重合;(2)中心对称图形也是一种特殊的旋转对称图形。
O
B
A
C
D
对称中心是 ______,
点O
点A的对称点是 ______,
点D的对称点是 ______,
点C
点B
平行四边形ABCD绕点O旋转180°后,能与本身重合。
这一类图形本身关于某点成中心对称。
名称 中心对称 中心对称图形
定义
性质
区别
联系
中心对称与中心对称图形的区别与联系
把一个图形绕着某一个点旋转180 ,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称,这两个图形中的对应点叫做关于中心的对称点
如果一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心
①两个图形完全重合;
②对应点连线都经过对称中心,并且被对称中心平分
________
①两个图形的关系
②对称点在两个图形上
①具有某种性质的一个图形
②对称点在一个图形上
若把中心对称图形的两部分分别看作两图,则它们成中心对称。若把中心对称的两图看作一个整体,则成为中心对称图形。
下列图形是中心对称图形吗?
小练习
认真观察旋转180°后……
都是中心对称图形。
图形的中心就是对称中心。
都是中心对称图形。
图形的中心就是对称中心。
线段、三角形、平行四边形、长方形、正方形、圆是中心对称图形吗?如果是,那么对称中心又在哪里?
1. 选择题:
(1)下列图形中即是轴对称图形又是中心对称图形的是( )
A. 角 B. 等边三角形 C. 线段 D. 平行四边形
C
(2)下列多边形中,是中心对称图形而不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
A
随堂练习
2. 判断下列说法是否正确。
(1)轴对称图形也是中心对称图形。( )
(2)旋转对称图形也是中心对称图形。( )
(3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( )
(4)角是轴对称图形也是中心对称图形。( )
(5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等。 ( )
×
√
×
√
×
3. 判断下列图形是否是中心对称图形
√
×
√
√
√
√
√
√
√
×
√
×
√
√
×
√
×
√
√
√
√
√
√
4. 观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
(1)
(3)
(2)
(4)
(5)
(6)
(3)(4)(6)
(1)
(2)(5)
5. 在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有______________
_______,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________.
①⑤⑥⑦⑧⑨
①②③④
①⑥⑦⑧⑨
⑥⑦⑧⑨
旋转前后的图形完全重合
轴对称图形
中心对称图形
有一条对称轴
——
直线
有一个对称中心
——
点
图形沿轴对折(翻转
180°
)
图形绕对称中心旋转
180°
翻转前后的图形完全重合
中心对称图形与轴对称图形的区别与联系
课堂小结
