2022版新教材高中数学第1章直线与方程本章达标测评(word版含答案)苏教版选择性必修第一册(Word含答案解析)
文档属性
| 名称 | 2022版新教材高中数学第1章直线与方程本章达标测评(word版含答案)苏教版选择性必修第一册(Word含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 128.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 00:00:00 | ||
图片预览




文档简介
本章达标检测
(满分:150分;时间:120分钟)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.直线x-y+a=0,a∈R的倾斜角为 ( )
A. B. C. D.
2.两直线x+y-1=0与2x+2y-3=0之间的距离为 ( )
A. B. C. D.
3.若直线2x+y+5=0与直线kx+2y=0互相垂直,则它们的交点坐标为 ( )
A.(-1,-3) B.(-2,-1)
C. D.(-1,-2)
4.已知直线l1:xsin α-2y+5=0,l2:x+(2-sin α)y+cos=0,若l1∥l2,则sin α= ( )
A.-1 B.0 C.1 D.-1或1
5.一束光线从点M(5,3)射出,经x轴反射后的光线经过点N(7,3),则反射光线所在的直线方程为 ( )
A.y=3x-18 B.y=-3x-12
C.y=3x+12 D.y=-3x+18
6.著名数学家华罗庚曾说过:“数形结合百般好,割裂分家万事休.”事实上,有很多代数问题可以转化为几何问题加以解决,如:可以转化为平面上点M(x,y)与点N(a,b)的距离.结合上述观点,可得f(x)=+的最小值为 ( )
A.5 B.
C. D.2+
7.设m∈R,动直线l1:x+my-1=0过定点A,动直线l2:mx-y-2m+=0过定点B,若直线l1与l2相交于点P(异于点A,B),则△PAB周长的最大值为 ( )
A.+2 B.2+1 C.+1 D.2+2
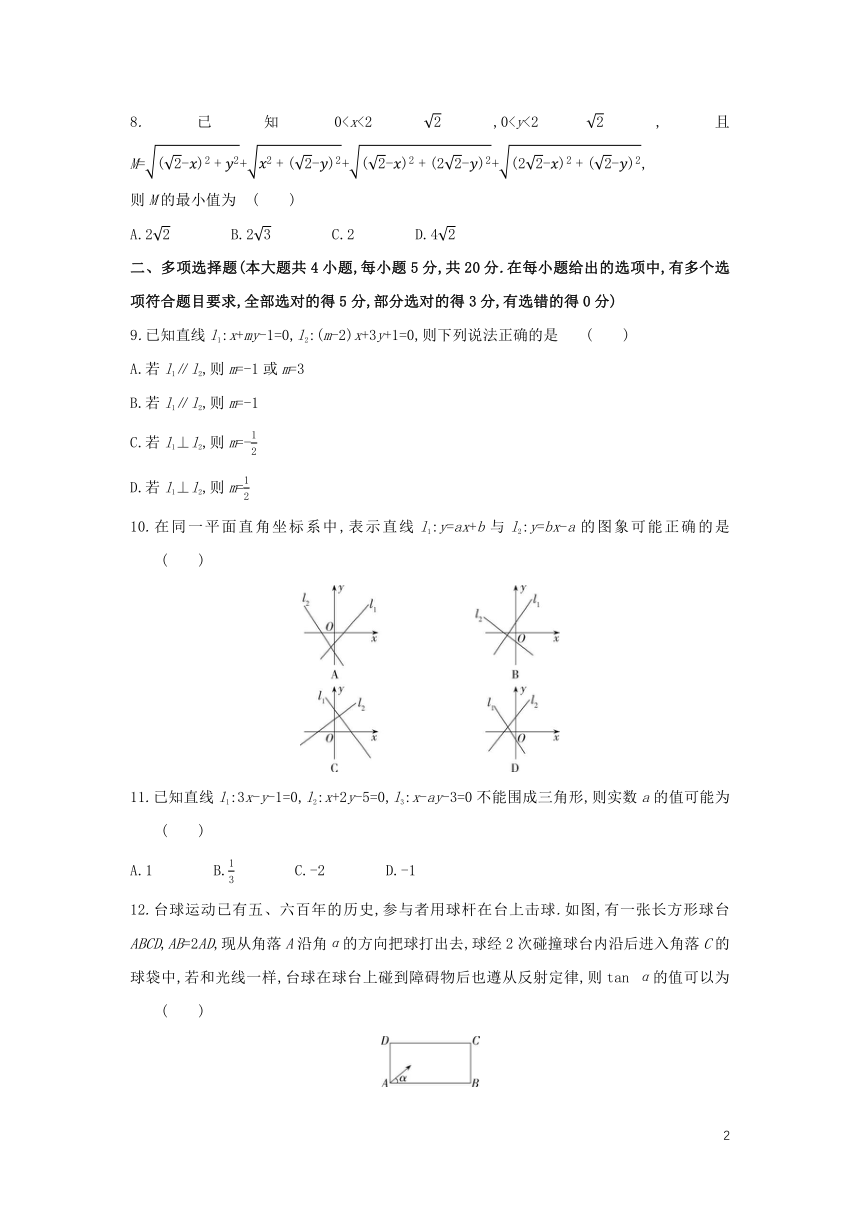
8.已知0则M的最小值为 ( )
A.2 B.2 C.2 D.4
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)
9.已知直线l1:x+my-1=0,l2:(m-2)x+3y+1=0,则下列说法正确的是 ( )
A.若l1∥l2,则m=-1或m=3
B.若l1∥l2,则m=-1
C.若l1⊥l2,则m=-
D.若l1⊥l2,则m=
10.在同一平面直角坐标系中,表示直线l1:y=ax+b与l2:y=bx-a的图象可能正确的是 ( )
11.已知直线l1:3x-y-1=0,l2:x+2y-5=0,l3:x-ay-3=0不能围成三角形,则实数a的值可能为 ( )
A.1 B. C.-2 D.-1
12.台球运动已有五、六百年的历史,参与者用球杆在台上击球.如图,有一张长方形球台ABCD,AB=2AD,现从角落A沿角α的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,若和光线一样,台球在球台上碰到障碍物后也遵从反射定律,则tan α的值可以为 ( )
A. B.
C.1 D.
三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上)
13.已知直线l:x-y-1=0,l1:2x-y-2=0,若直线l2与l1关于l对称,则l2的方程为 .
14.若动点A、B分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,则线段AB的中点M到原点距离O的最小值为 .
15.数学选修课中,同学们进行节能住房设计,在分析气候和民俗后,设计出房屋的剖面图(如图所示).屋顶所在直线的方程分别是y=x+3和y=-x+5,为保证采光,竖直窗户的高度设计为1 m,那么点A的横坐标是 .
16.已知点A(4,5),点B在x轴上,点C在2x-y+2=0上,则△ABC周长的最小值为 ,此时点C的坐标为 .(第一个空3分,第二个空2分)
四、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知直线l1:2x+y-2=0;l2:mx+4y+n=0(m,n为常数).
(1)若l1⊥l2,求m的值;
(2)若l1∥l2,且它们的距离为,求m,n的值.
18.(本小题满分12分)已知三角形的顶点为A(2,3),B(0,-1),C(-2,1).
(1)求直线AC的方程;
(2)求点B关于直线AC的对称点D的坐标;
(3)若直线l过点B且与直线AC交于点E,BE=3,求直线l的方程.
19. (本小题满分12分)直线过点P且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在直线满足下列条件:(1)△AOB的周长为12;(2)△AOB的面积为6.若存在,求出直线的方程;若不存在,请说明理由.
20.(本小题满分12分)为了绿化城市,准备在如图所示的区域ABCDE内修建一个矩形的草坪PQRD,其中∠AED=∠EDC=∠DCB=90°,点Q在AB上,且PQ∥CD,QR⊥CD,经测量BC=70 m,CD=80 m,DE=100 m,AE=60 m,则应如何设计才能使草坪的占地面积最大 并求出最大面积.(结果精确到1 m2)
21. (本小题满分12分)设集合L={l|直线l与直线y=3x相交,且以交点的横坐标为斜率}.
(1)是否存在直线l0使l0∈L,且l0过点(1,5) 若存在,请写出l0的方程,若不存在,请说明理由;
(2)点P(-3,5)到集合L中的哪一条直线的距离最小
(3)设a∈(0,+∞),点Q(-3,a)到集合L中直线的距离的最小值为f(a),求f(a)的解析式.
22.(本小题满分12分)如图所示,在平面直角坐标系xOy中,第一象限内有定点C和射线OA,已知直线OA,OC的倾斜角分别为α,β,tan α=3,tan β=,OC=13a(0(1)求点C的坐标(用a表示);
(2)求△OAM的面积S关于m的表达式S=f(m);
(3)求△OAM的面积取得最小时,直线AC的方程.
答案全解全析
本章达标检测
一、单项选择题
1.A ∵直线x-y+a=0,a∈R的斜率为=,∴它的倾斜角为.故选A.
2.B 两直线方程分别为x+y-1=0与2x+2y-3=0,即2x+2y-2=0与2x+2y-3=0,
故它们之间的距离为=.故选B.
3.B ∵直线2x+y+5=0与直线kx+2y=0互相垂直,∴2k+1×2=0,解得k=-1,
∴直线kx+2y=0即-x+2y=0,
由得∴两直线的交点坐标为(-2,-1),
故选B.
4.A ∵直线l1:xsin α-2y+5=0,l2:x+(2-sin α)y+cos=0,l1∥l2,
∴sin α(2-sin α)=-2×,且5×(2-sin α)≠-2×cos,解得sin α=3(舍去)或sin α=-1,
故选A.
5.A 设点M(5,3)关于x轴对称的点为M',则M'(5,-3),则M'(5,-3)在反射光线的反向延长线上,
则kM'N==3,
所以反射光线所在的直线方程为y-3=3(x-7),即y=3x-18.
故选A.
6.B f(x)=+=+,
表示平面上点M(x,0)与点A(-5,2),B(-3,-3)的距离之和,
则f(x)的最小值为AB==,故选B.
7.D 直线l1:x+my-1=0过定点A(1,0),
直线l2:mx-y-2m+=0,即m(x-2)=y-,可得直线l2过定点B(2,),
∵1×m+(-1)×m=0,
∴l1与l2始终垂直,
又P是直线l1与l2的交点,
∴PA⊥PB,∴PA2+PB2=AB2=4.
由不等式的相关知识可知2(PA2+PB2)≥(PA+PB)2,
即PA+PB≤=2,
当且仅当PA=PB=时,等号成立,
∴△PAB周长的最大值为2+2.
故选D.
8.D 根据题意可知表示点(x,y)与点A(,0)间的距离;
表示点(x,y)与点B(0,)间的距离;
表示点(x,y)与点C(,2)间的距离;
表示点(x,y)与点D(2,)间的距离.
则M表示点(x,y)到A、B、C、D四个点的距离之和的最小值.
如图:
∵+取最小值时点(x,y)在线段AC上,
+取最小值时点(x,y)在线段BD上,
∴当M取最小值时,点(x,y)既在线段AC上,又在线段BD上,
∴点(x,y)即为图中点P,
∴M的最小值为AC+BD=4.
故选D.
二、多项选择题
9.AD 已知直线l1:x+my-1=0,l2:(m-2)x+3y+1=0,
若l1∥l2,则1×3-m(m-2)=0,且m×1≠-1×3,解得m=3或m=-1,故A正确,B不正确.
若l1⊥l2,则1×(m-2)+m×3=0,解得m=,故C不正确,D正确.
故选AD.
10.AC 由题图A可得直线l1的斜率a>0,在y轴上的截距b<0;
而l2的斜率b<0,在y轴上的截距-a<0,即a>0,故A能成立.
由题图B可得直线l1的斜率a>0,在y轴上的截距b>0;
而l2的斜率b<0,矛盾,故B不能成立.
由题图C可得直线l1的斜率a<0,在y轴上的截距b>0;
而l2的斜率b>0,在y轴上的截距-a>0,即a<0,故C能成立.
由题图D可得直线l1的斜率a<0,在y轴上的截距b<0;
而l2的斜率b>0,在y轴上的截距-a>0,即a<0,矛盾,故D不能成立.
故选AC.
11.BCD ∵直线l1:3x-y-1=0,l2:x+2y-5=0,l3:x-ay-3=0不能围成三角形,
∴有2条直线平行或者三条直线经过同一个点.
若其中有2条直线平行,则=3或=-,解得a=或a=-2.
若三条直线经过同一个点,则直线l1:3x-y-1=0和直线l2:x+2y-5=0的交点(1,2)在l3上,故1-2a-3=0,解得a=-1.
综上,实数a的值可能为,-2,-1.
故选BCD.
12.AD 如图1:
图1
设A关于DC的对称点为E,C关于AB的对称点为F,
则tan α===.
如图2:
图2
设点A关于BC的对称点为P,C关于AD的对称点为M,
则tan α===.
故选AD.
三、填空题
13.答案 x-2y-1=0
解析 联立
解得
所以三条直线的交点坐标为(1,0),
在l1上取点(2,2),依题意知该点关于l的对称点(3,1)在l2上,
则l2的方程为=,化简得x-2y-1=0.
14.答案 3
解析 ∵A在直线l1上,B在直线l2上,点M是线段AB的中点,∴点M在到两直线l1与l2距离相等的直线上,
∵直线l1:x+y-7=0和l2:x+y-5=0,
∴点M所在直线的方程为x+y-6=0,
则MO的最小值为=3.
15.答案 4.5
解析 根据题意,设点A的横坐标为m,则点A的坐标为(m,0),
对于直线y=x+3,当x=m时,y=+3,
对于直线y=-x+5,当x=m时,y=-+5,
若满足竖直窗户的高度设计为1 m,
则-=-2=1,
解得m=4.5,故点A的横坐标为4.5.
16.答案 4;(1,4)
解析 按题意画图,设点B的坐标为(m,0),点A关于直线2x-y+2=0的对称点D的坐标为(a,b),
则线段AD的中点E的坐标为,
则
即解得即D(0,7),
易知点A关于x轴对称的点的坐标为P(4,-5),
则当D,C,B,P四点共线时,△ABC的周长最小,最小为DP==4.
则直线DP的方程为=,即3x+y-7=0,
联立解得C(1,4).
四、解答题
17.解析 (1)若l1⊥l2,则-2·=-1, (3分)
解得m=-2,故m的值为-2. (5分)
(2)若l1∥l2,则=≠,解得m=8,n≠-8, (8分)
故直线l1:8x+4y-8=0,l2:8x+4y+n=0.
故=,
解得n=12或n=-28.
故m的值为8,n的值为12或-28. (10分)
18.解析 (1)因为直线AC的斜率为=,
所以直线AC的方程为y-3=(x-2),
即x-2y+4=0. (4分)
(2)设点D的坐标为(m,n),
则解得
故点D的坐标为. (8分)
(3)设点E的坐标为,
∵BE=3,∴=3,
解得t=0或t=-, (10分)
∴点E的坐标为(0,2)或,
∴直线l的方程为x=0或3x+4y+4=0. (12分)
易错警示
求解直线方程时应该注意以下问题:
(1)根据斜率求倾斜角时,要注意倾斜角的范围;
(2)若不能判断直线的斜率是否存在,则应对斜率存在与不存在加以讨论;
(3)在用截距式表示直线时,应先判断截距是不是0,若不确定,则需分类讨论.
19.解析 存在.设直线方程为+=1(a>0,b>0),
若满足条件(1),则a+b+=12.① (3分)
∵直线过点P,∴+=1.②
由①②可得5a2-32a+48=0,
解得或 (6分)
则直线的方程为+=1或+=1,即3x+4y-12=0或15x+8y-36=0.
若满足条件(2),则ab=12,③ (8分)
由题意得,+=1,④
由③④可得a2-6a+8=0,
解得或 (10分)
则直线的方程为+=1或+=1,即3x+4y-12=0或3x+y-6=0. (11分)
综上所述,存在同时满足(1)(2)两个条件的直线方程,为3x+4y-12=0. (12分)
20.解析 如图,以BC边所在直线为x轴,以AE边所在直线为y轴,建立平面直角坐标系,则A(0,20),B(30,0). (2分)
所以直线AB的方程为+=1,即y=20-x, (5分)
设Q,则矩形PQRD的面积S=(100-x), (8分)
即S=-x2+x+6 000=-(x-5)2+6 000+(0≤x≤30), (10分)
易得当x=5,y=时,S取得最大值,最大值约为6 017 m2. (12分)
21.解析 (1)假设存在直线l0使l0∈L,且l0过点(1,5),
设l0的方程为y-5=k(x-1)(k≠3),
联立 得x=, (2分)
则=k,化简得k2-4k+5=0,此方程无解,
故不存在直线l0符合题意. (4分)
(2)设直线l的方程为y=k1x+b(k1≠3),联立得x=,则=k1,化简得b=3k1-,故点P(-3,5)到直线l的距离为==+≥4,当且仅当k1=±时取等号. (6分)
当k1=时,b=3-3,直线方程为y=x+3-3,
当k1=-时,b=-3-3,直线方程为y=-x-3-3,
故点P(-3,5)与集合L中的直线y=x+3-3和y=-x-3-3的距离最小. (8分)
(3)设直线l的方程为y=k2x+m(k2≠3),联立得x=,则=k2,化简得m=3k2-,故点Q(-3,a)到直线l的距离d===+.
当a>2时,d≥2,当且仅当k2=±时取等号, (10分)
当0综上,f(a)= (12分)
22.解析 (1) ∵β∈[0,π),tan β=,
∴sin β=,cos β=,又OC=13a,
∴C(12a,5a). (2分)
(2)直线OA:y=3x,∵M,C,A共线,∴当AM⊥x轴时,M(12a,0),A(12a,36a),当AM不与x轴垂直时,设A(x0,3x0),由kMC=kMA,得=,
解得x0=,经检验,当AM⊥x轴时,A点横坐标也满足此式,∴S=f(m)=. (5分)
(3)解法一:S=f(m)==×,
记t=,g(t)=-31at2+3t=-31a×+,t∈. (8分)
①若≤,即3≤a≤4,则函数g(t)在上递减,当且仅当t=,即m=62时,g(t)取得最大值,即f(m)取得最小值,此时M(62,0),直线AC的方程为5ax-(12a-62)y-310a=0. (10分)
②若<<,即0解法二:记3m-31a=t,t∈(0,186-31a],
则S=h(t)=·=·,t∈(0,186-31a]. (8分)
①若3≤a≤4,则186-31a≤31a,则h(t)在(0,186-31a]上递减,当且仅当t=186-31a,即m=62时,h(t)取得最小值,此时M(62,0),直线AC的方程为5ax-(12a-62)·y-310a=0. (10分)
②若031a,则h(t)在(0,31a)上递减, 在(31a,186-31a]上递增,
当且仅当t=31a,即m=时,h(t)取得最小值,此时M,直线AC的方程为15x+26y-310a=0. (12分)
16
(满分:150分;时间:120分钟)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.直线x-y+a=0,a∈R的倾斜角为 ( )
A. B. C. D.
2.两直线x+y-1=0与2x+2y-3=0之间的距离为 ( )
A. B. C. D.
3.若直线2x+y+5=0与直线kx+2y=0互相垂直,则它们的交点坐标为 ( )
A.(-1,-3) B.(-2,-1)
C. D.(-1,-2)
4.已知直线l1:xsin α-2y+5=0,l2:x+(2-sin α)y+cos=0,若l1∥l2,则sin α= ( )
A.-1 B.0 C.1 D.-1或1
5.一束光线从点M(5,3)射出,经x轴反射后的光线经过点N(7,3),则反射光线所在的直线方程为 ( )
A.y=3x-18 B.y=-3x-12
C.y=3x+12 D.y=-3x+18
6.著名数学家华罗庚曾说过:“数形结合百般好,割裂分家万事休.”事实上,有很多代数问题可以转化为几何问题加以解决,如:可以转化为平面上点M(x,y)与点N(a,b)的距离.结合上述观点,可得f(x)=+的最小值为 ( )
A.5 B.
C. D.2+
7.设m∈R,动直线l1:x+my-1=0过定点A,动直线l2:mx-y-2m+=0过定点B,若直线l1与l2相交于点P(异于点A,B),则△PAB周长的最大值为 ( )
A.+2 B.2+1 C.+1 D.2+2
8.已知0
A.2 B.2 C.2 D.4
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)
9.已知直线l1:x+my-1=0,l2:(m-2)x+3y+1=0,则下列说法正确的是 ( )
A.若l1∥l2,则m=-1或m=3
B.若l1∥l2,则m=-1
C.若l1⊥l2,则m=-
D.若l1⊥l2,则m=
10.在同一平面直角坐标系中,表示直线l1:y=ax+b与l2:y=bx-a的图象可能正确的是 ( )
11.已知直线l1:3x-y-1=0,l2:x+2y-5=0,l3:x-ay-3=0不能围成三角形,则实数a的值可能为 ( )
A.1 B. C.-2 D.-1
12.台球运动已有五、六百年的历史,参与者用球杆在台上击球.如图,有一张长方形球台ABCD,AB=2AD,现从角落A沿角α的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,若和光线一样,台球在球台上碰到障碍物后也遵从反射定律,则tan α的值可以为 ( )
A. B.
C.1 D.
三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上)
13.已知直线l:x-y-1=0,l1:2x-y-2=0,若直线l2与l1关于l对称,则l2的方程为 .
14.若动点A、B分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,则线段AB的中点M到原点距离O的最小值为 .
15.数学选修课中,同学们进行节能住房设计,在分析气候和民俗后,设计出房屋的剖面图(如图所示).屋顶所在直线的方程分别是y=x+3和y=-x+5,为保证采光,竖直窗户的高度设计为1 m,那么点A的横坐标是 .
16.已知点A(4,5),点B在x轴上,点C在2x-y+2=0上,则△ABC周长的最小值为 ,此时点C的坐标为 .(第一个空3分,第二个空2分)
四、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知直线l1:2x+y-2=0;l2:mx+4y+n=0(m,n为常数).
(1)若l1⊥l2,求m的值;
(2)若l1∥l2,且它们的距离为,求m,n的值.
18.(本小题满分12分)已知三角形的顶点为A(2,3),B(0,-1),C(-2,1).
(1)求直线AC的方程;
(2)求点B关于直线AC的对称点D的坐标;
(3)若直线l过点B且与直线AC交于点E,BE=3,求直线l的方程.
19. (本小题满分12分)直线过点P且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在直线满足下列条件:(1)△AOB的周长为12;(2)△AOB的面积为6.若存在,求出直线的方程;若不存在,请说明理由.
20.(本小题满分12分)为了绿化城市,准备在如图所示的区域ABCDE内修建一个矩形的草坪PQRD,其中∠AED=∠EDC=∠DCB=90°,点Q在AB上,且PQ∥CD,QR⊥CD,经测量BC=70 m,CD=80 m,DE=100 m,AE=60 m,则应如何设计才能使草坪的占地面积最大 并求出最大面积.(结果精确到1 m2)
21. (本小题满分12分)设集合L={l|直线l与直线y=3x相交,且以交点的横坐标为斜率}.
(1)是否存在直线l0使l0∈L,且l0过点(1,5) 若存在,请写出l0的方程,若不存在,请说明理由;
(2)点P(-3,5)到集合L中的哪一条直线的距离最小
(3)设a∈(0,+∞),点Q(-3,a)到集合L中直线的距离的最小值为f(a),求f(a)的解析式.
22.(本小题满分12分)如图所示,在平面直角坐标系xOy中,第一象限内有定点C和射线OA,已知直线OA,OC的倾斜角分别为α,β,tan α=3,tan β=,OC=13a(0
(2)求△OAM的面积S关于m的表达式S=f(m);
(3)求△OAM的面积取得最小时,直线AC的方程.
答案全解全析
本章达标检测
一、单项选择题
1.A ∵直线x-y+a=0,a∈R的斜率为=,∴它的倾斜角为.故选A.
2.B 两直线方程分别为x+y-1=0与2x+2y-3=0,即2x+2y-2=0与2x+2y-3=0,
故它们之间的距离为=.故选B.
3.B ∵直线2x+y+5=0与直线kx+2y=0互相垂直,∴2k+1×2=0,解得k=-1,
∴直线kx+2y=0即-x+2y=0,
由得∴两直线的交点坐标为(-2,-1),
故选B.
4.A ∵直线l1:xsin α-2y+5=0,l2:x+(2-sin α)y+cos=0,l1∥l2,
∴sin α(2-sin α)=-2×,且5×(2-sin α)≠-2×cos,解得sin α=3(舍去)或sin α=-1,
故选A.
5.A 设点M(5,3)关于x轴对称的点为M',则M'(5,-3),则M'(5,-3)在反射光线的反向延长线上,
则kM'N==3,
所以反射光线所在的直线方程为y-3=3(x-7),即y=3x-18.
故选A.
6.B f(x)=+=+,
表示平面上点M(x,0)与点A(-5,2),B(-3,-3)的距离之和,
则f(x)的最小值为AB==,故选B.
7.D 直线l1:x+my-1=0过定点A(1,0),
直线l2:mx-y-2m+=0,即m(x-2)=y-,可得直线l2过定点B(2,),
∵1×m+(-1)×m=0,
∴l1与l2始终垂直,
又P是直线l1与l2的交点,
∴PA⊥PB,∴PA2+PB2=AB2=4.
由不等式的相关知识可知2(PA2+PB2)≥(PA+PB)2,
即PA+PB≤=2,
当且仅当PA=PB=时,等号成立,
∴△PAB周长的最大值为2+2.
故选D.
8.D 根据题意可知表示点(x,y)与点A(,0)间的距离;
表示点(x,y)与点B(0,)间的距离;
表示点(x,y)与点C(,2)间的距离;
表示点(x,y)与点D(2,)间的距离.
则M表示点(x,y)到A、B、C、D四个点的距离之和的最小值.
如图:
∵+取最小值时点(x,y)在线段AC上,
+取最小值时点(x,y)在线段BD上,
∴当M取最小值时,点(x,y)既在线段AC上,又在线段BD上,
∴点(x,y)即为图中点P,
∴M的最小值为AC+BD=4.
故选D.
二、多项选择题
9.AD 已知直线l1:x+my-1=0,l2:(m-2)x+3y+1=0,
若l1∥l2,则1×3-m(m-2)=0,且m×1≠-1×3,解得m=3或m=-1,故A正确,B不正确.
若l1⊥l2,则1×(m-2)+m×3=0,解得m=,故C不正确,D正确.
故选AD.
10.AC 由题图A可得直线l1的斜率a>0,在y轴上的截距b<0;
而l2的斜率b<0,在y轴上的截距-a<0,即a>0,故A能成立.
由题图B可得直线l1的斜率a>0,在y轴上的截距b>0;
而l2的斜率b<0,矛盾,故B不能成立.
由题图C可得直线l1的斜率a<0,在y轴上的截距b>0;
而l2的斜率b>0,在y轴上的截距-a>0,即a<0,故C能成立.
由题图D可得直线l1的斜率a<0,在y轴上的截距b<0;
而l2的斜率b>0,在y轴上的截距-a>0,即a<0,矛盾,故D不能成立.
故选AC.
11.BCD ∵直线l1:3x-y-1=0,l2:x+2y-5=0,l3:x-ay-3=0不能围成三角形,
∴有2条直线平行或者三条直线经过同一个点.
若其中有2条直线平行,则=3或=-,解得a=或a=-2.
若三条直线经过同一个点,则直线l1:3x-y-1=0和直线l2:x+2y-5=0的交点(1,2)在l3上,故1-2a-3=0,解得a=-1.
综上,实数a的值可能为,-2,-1.
故选BCD.
12.AD 如图1:
图1
设A关于DC的对称点为E,C关于AB的对称点为F,
则tan α===.
如图2:
图2
设点A关于BC的对称点为P,C关于AD的对称点为M,
则tan α===.
故选AD.
三、填空题
13.答案 x-2y-1=0
解析 联立
解得
所以三条直线的交点坐标为(1,0),
在l1上取点(2,2),依题意知该点关于l的对称点(3,1)在l2上,
则l2的方程为=,化简得x-2y-1=0.
14.答案 3
解析 ∵A在直线l1上,B在直线l2上,点M是线段AB的中点,∴点M在到两直线l1与l2距离相等的直线上,
∵直线l1:x+y-7=0和l2:x+y-5=0,
∴点M所在直线的方程为x+y-6=0,
则MO的最小值为=3.
15.答案 4.5
解析 根据题意,设点A的横坐标为m,则点A的坐标为(m,0),
对于直线y=x+3,当x=m时,y=+3,
对于直线y=-x+5,当x=m时,y=-+5,
若满足竖直窗户的高度设计为1 m,
则-=-2=1,
解得m=4.5,故点A的横坐标为4.5.
16.答案 4;(1,4)
解析 按题意画图,设点B的坐标为(m,0),点A关于直线2x-y+2=0的对称点D的坐标为(a,b),
则线段AD的中点E的坐标为,
则
即解得即D(0,7),
易知点A关于x轴对称的点的坐标为P(4,-5),
则当D,C,B,P四点共线时,△ABC的周长最小,最小为DP==4.
则直线DP的方程为=,即3x+y-7=0,
联立解得C(1,4).
四、解答题
17.解析 (1)若l1⊥l2,则-2·=-1, (3分)
解得m=-2,故m的值为-2. (5分)
(2)若l1∥l2,则=≠,解得m=8,n≠-8, (8分)
故直线l1:8x+4y-8=0,l2:8x+4y+n=0.
故=,
解得n=12或n=-28.
故m的值为8,n的值为12或-28. (10分)
18.解析 (1)因为直线AC的斜率为=,
所以直线AC的方程为y-3=(x-2),
即x-2y+4=0. (4分)
(2)设点D的坐标为(m,n),
则解得
故点D的坐标为. (8分)
(3)设点E的坐标为,
∵BE=3,∴=3,
解得t=0或t=-, (10分)
∴点E的坐标为(0,2)或,
∴直线l的方程为x=0或3x+4y+4=0. (12分)
易错警示
求解直线方程时应该注意以下问题:
(1)根据斜率求倾斜角时,要注意倾斜角的范围;
(2)若不能判断直线的斜率是否存在,则应对斜率存在与不存在加以讨论;
(3)在用截距式表示直线时,应先判断截距是不是0,若不确定,则需分类讨论.
19.解析 存在.设直线方程为+=1(a>0,b>0),
若满足条件(1),则a+b+=12.① (3分)
∵直线过点P,∴+=1.②
由①②可得5a2-32a+48=0,
解得或 (6分)
则直线的方程为+=1或+=1,即3x+4y-12=0或15x+8y-36=0.
若满足条件(2),则ab=12,③ (8分)
由题意得,+=1,④
由③④可得a2-6a+8=0,
解得或 (10分)
则直线的方程为+=1或+=1,即3x+4y-12=0或3x+y-6=0. (11分)
综上所述,存在同时满足(1)(2)两个条件的直线方程,为3x+4y-12=0. (12分)
20.解析 如图,以BC边所在直线为x轴,以AE边所在直线为y轴,建立平面直角坐标系,则A(0,20),B(30,0). (2分)
所以直线AB的方程为+=1,即y=20-x, (5分)
设Q,则矩形PQRD的面积S=(100-x), (8分)
即S=-x2+x+6 000=-(x-5)2+6 000+(0≤x≤30), (10分)
易得当x=5,y=时,S取得最大值,最大值约为6 017 m2. (12分)
21.解析 (1)假设存在直线l0使l0∈L,且l0过点(1,5),
设l0的方程为y-5=k(x-1)(k≠3),
联立 得x=, (2分)
则=k,化简得k2-4k+5=0,此方程无解,
故不存在直线l0符合题意. (4分)
(2)设直线l的方程为y=k1x+b(k1≠3),联立得x=,则=k1,化简得b=3k1-,故点P(-3,5)到直线l的距离为==+≥4,当且仅当k1=±时取等号. (6分)
当k1=时,b=3-3,直线方程为y=x+3-3,
当k1=-时,b=-3-3,直线方程为y=-x-3-3,
故点P(-3,5)与集合L中的直线y=x+3-3和y=-x-3-3的距离最小. (8分)
(3)设直线l的方程为y=k2x+m(k2≠3),联立得x=,则=k2,化简得m=3k2-,故点Q(-3,a)到直线l的距离d===+.
当a>2时,d≥2,当且仅当k2=±时取等号, (10分)
当0
22.解析 (1) ∵β∈[0,π),tan β=,
∴sin β=,cos β=,又OC=13a,
∴C(12a,5a). (2分)
(2)直线OA:y=3x,∵M,C,A共线,∴当AM⊥x轴时,M(12a,0),A(12a,36a),当AM不与x轴垂直时,设A(x0,3x0),由kMC=kMA,得=,
解得x0=,经检验,当AM⊥x轴时,A点横坐标也满足此式,∴S=f(m)=. (5分)
(3)解法一:S=f(m)==×,
记t=,g(t)=-31at2+3t=-31a×+,t∈. (8分)
①若≤,即3≤a≤4,则函数g(t)在上递减,当且仅当t=,即m=62时,g(t)取得最大值,即f(m)取得最小值,此时M(62,0),直线AC的方程为5ax-(12a-62)y-310a=0. (10分)
②若<<,即0
则S=h(t)=·=·,t∈(0,186-31a]. (8分)
①若3≤a≤4,则186-31a≤31a,则h(t)在(0,186-31a]上递减,当且仅当t=186-31a,即m=62时,h(t)取得最小值,此时M(62,0),直线AC的方程为5ax-(12a-62)·y-310a=0. (10分)
②若0
当且仅当t=31a,即m=时,h(t)取得最小值,此时M,直线AC的方程为15x+26y-310a=0. (12分)
16
