2021—2022学年人教版八年级数学下册19.1.1变量与函数课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册19.1.1变量与函数课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 146.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 19:28:03 | ||
图片预览

文档简介
2021——2022学年度人教版八年级数学下册 第十九章 一次函数
19.1.1 变量与函数 课后练习
一、选择题
1.下列变量之间是函数关系的有( )
①正方形的周长C与边长a;②矩形的周长C与宽a;③圆的面积S与半径R;④y=2x-3中的y与x
A.4个 B.3个 C.2个 D.1个
2.据省统计局公布的数据,安徽省2019年第二季度GDP总值约为7.9千亿元人民币,若我省后两个季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( ).
A. B.
C. D.
3.某种商品的售价为每件元,若按现售价的折进行促销,设顾客购买件需要元,则与的函数解析式为( )
A. B.
C. D.
4.函数的自变量的取值范围为( )
A. B. C. D.
5.在圆的面积计算公式,其中为圆的半径,则变量是( )
A. B. C., D.,
6.当实数的取值使得有意义时,函数中的取值范围是( )
A. B. C. D.
7.关于函数,下列说法正确的是( )
A.自变量的取值范围是 B.时, 函数的值是0
C.当时,函数的值大于0 D.A、B、C都不对
8.一个物体自由下落时,它所经过的距离h(米)和时间t(秒)之间的关系我们可以用来估算.假设物体从超过10米的高度自由下落,小明要计算这个物体每经过1米所需要的时间,则经过第5个1米时所需要的时间最接近( )
A.1秒 B.0.4秒 C.0.2秒 D.0.1秒
9.已知函数y= 当y=5时, x的值是 ( )
A.6 B.-2 C.-2或6 D.±2或6
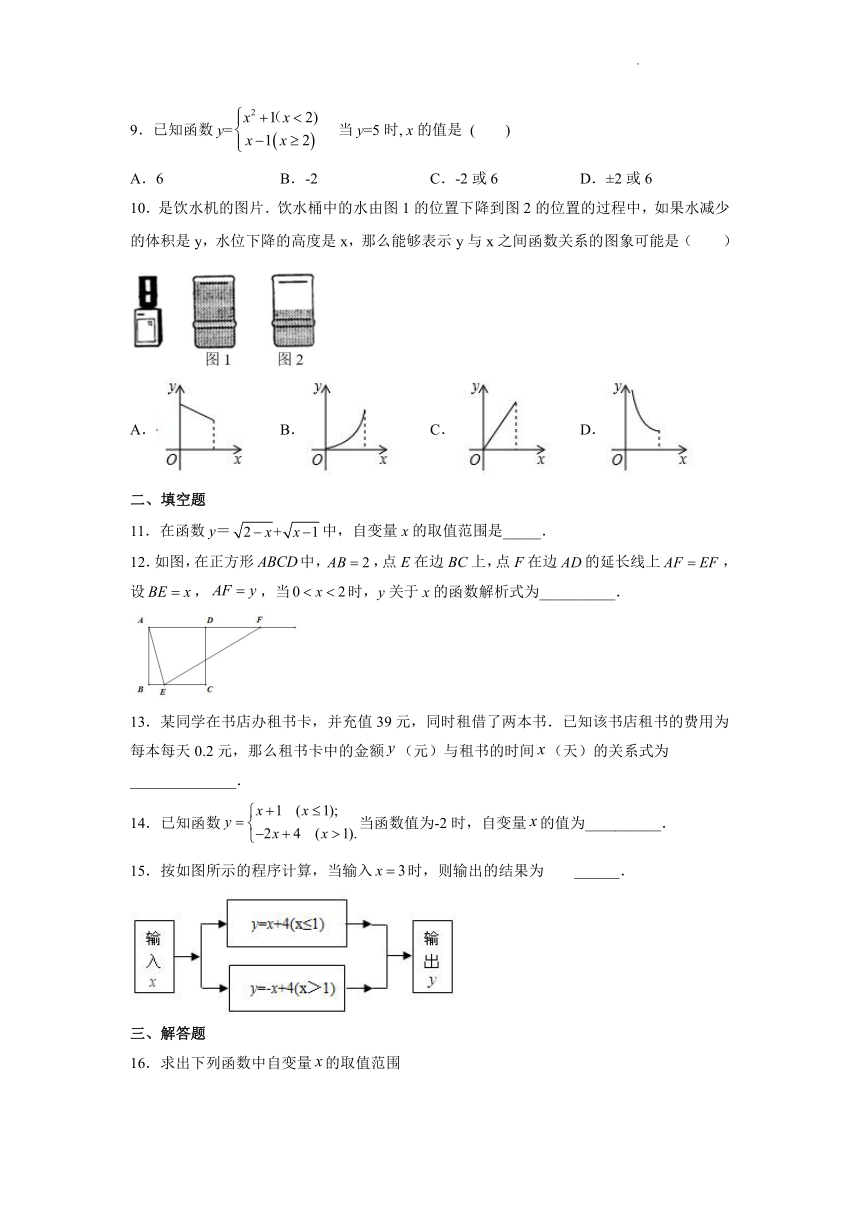
10.是饮水机的图片.饮水桶中的水由图1的位置下降到图2的位置的过程中,如果水减少的体积是y,水位下降的高度是x,那么能够表示y与x之间函数关系的图象可能是( )
A. B. C. D.
二、填空题
11.在函数y=中,自变量x的取值范围是_____.
12.如图,在正方形中,,点E在边BC上,点F在边的延长线上,设,,当时,y关于x的函数解析式为__________.
13.某同学在书店办租书卡,并充值39元,同时租借了两本书.已知该书店租书的费用为每本每天0.2元,那么租书卡中的金额(元)与租书的时间(天)的关系式为______________.
14.已知函数当函数值为-2时,自变量的值为__________.
15.按如图所示的程序计算,当输入时,则输出的结果为______.
三、解答题
16.求出下列函数中自变量的取值范围
(1)
(2)
(3)
17.(1)当x为何整数时,分式的值为正整数?
(2)已知函数自变量取值范围为整数,求y的最大、最小值.
18.如图,用长为20m的篱笆(粗线部分)和墙围成一块菜地,四边形ABCG和四边形DEFG均是正方形,在边DE处有2米宽的入口MN(此处安装简易门).设 (m), (m).
(1)求y与x间的关系式.
(2)若菜地面积为S(m2),求S与x间的关系式.
19.如图,在矩形ABCD中,对角线AC和BD相交于点O,若∠AOB=60°,AD=8,M是线段AD上的一个动点(不与端点A、D重合),MF⊥BD,ME⊥AC,垂足分别为点F、E.
(1)求AB的长;
(2)设ME=x,MF=y,求y关于x的函数关系式
20.如果有一个四位数,百位比千位大1,个位比十位大1,那么我们把这个四位数称为“阶梯数”,把的千位和十位对调,把百位和个位对调得到的数为,并规定
.比如1256,且,1256为“阶梯数”,
,再比如1246,,1246不是“阶梯数”.
(1)判断3467和2368是不是“阶梯数”,并说明理由,如果是“阶梯数”的请求出其的值;
(2)已知,(,,,)且和都是“阶梯数”,是一个完全平方数,能被11整除,求的值.
21.如图所示,在中,底边,高,E为上一动点,当点E从点D向点A运动时,的面积发生了变化.
(1)若设长为,的面积为y,求y与x之间的关系式及x的范围.
(2)当长度为时,的面积y是多少?
22.为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下,制成表格:
汽车行驶的时间t(小时) 0 1 2 3 …
油箱中的剩余油量Q(升) 100 94 88 82 …
(1)如表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据表可知,该车油箱的大小为 升,每小时耗油 升;
(3)两个变量Q与t之间的关系式为 .
23.如果3个数位相同的自然数,,满足:,且各数位上的数字全部相同,则称数和数是一对“黄金搭档数”.例如:因为123,765,888都是三位数,,所以123和是一对“黄金搭档数”.再如:因为26,29,55都是两位数,,所以26和29是一对“黄金搭档数”.
(1)若326与一个个位上的数字是3的数是一对“黄金搭档数”,389与一个个位上的数字是8的数是一对“黄金搭档数”,直接写出和的值;
(2)若,,且,和是一对“黄金搭档数”,求这样的“黄金搭档数”一共有多少对
【参考答案】
1.B 2.D 3.C 4.C 5.D 6.B 7.C 8.D 9.C 10.C
11.1≤x≤2
12.
13.
14.或
15.1
16.(1)且;(2)且;(3)
17.(1);(2)y最大为3,最小为1
18.(1);(2)S
19.(1);(2)()
20.(1)3467为“阶梯数”;2368不是“阶梯数”,;(2)的值为5746或9046.
21.(1)y=4x,0≤x≤6;(2)12cm2.
22.(1)汽车行驶时间t;汽车油箱的剩余油量Q;(2)100,6;(3)Q=100-t
23.(1);(2)对.
19.1.1 变量与函数 课后练习
一、选择题
1.下列变量之间是函数关系的有( )
①正方形的周长C与边长a;②矩形的周长C与宽a;③圆的面积S与半径R;④y=2x-3中的y与x
A.4个 B.3个 C.2个 D.1个
2.据省统计局公布的数据,安徽省2019年第二季度GDP总值约为7.9千亿元人民币,若我省后两个季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( ).
A. B.
C. D.
3.某种商品的售价为每件元,若按现售价的折进行促销,设顾客购买件需要元,则与的函数解析式为( )
A. B.
C. D.
4.函数的自变量的取值范围为( )
A. B. C. D.
5.在圆的面积计算公式,其中为圆的半径,则变量是( )
A. B. C., D.,
6.当实数的取值使得有意义时,函数中的取值范围是( )
A. B. C. D.
7.关于函数,下列说法正确的是( )
A.自变量的取值范围是 B.时, 函数的值是0
C.当时,函数的值大于0 D.A、B、C都不对
8.一个物体自由下落时,它所经过的距离h(米)和时间t(秒)之间的关系我们可以用来估算.假设物体从超过10米的高度自由下落,小明要计算这个物体每经过1米所需要的时间,则经过第5个1米时所需要的时间最接近( )
A.1秒 B.0.4秒 C.0.2秒 D.0.1秒
9.已知函数y= 当y=5时, x的值是 ( )
A.6 B.-2 C.-2或6 D.±2或6
10.是饮水机的图片.饮水桶中的水由图1的位置下降到图2的位置的过程中,如果水减少的体积是y,水位下降的高度是x,那么能够表示y与x之间函数关系的图象可能是( )
A. B. C. D.
二、填空题
11.在函数y=中,自变量x的取值范围是_____.
12.如图,在正方形中,,点E在边BC上,点F在边的延长线上,设,,当时,y关于x的函数解析式为__________.
13.某同学在书店办租书卡,并充值39元,同时租借了两本书.已知该书店租书的费用为每本每天0.2元,那么租书卡中的金额(元)与租书的时间(天)的关系式为______________.
14.已知函数当函数值为-2时,自变量的值为__________.
15.按如图所示的程序计算,当输入时,则输出的结果为______.
三、解答题
16.求出下列函数中自变量的取值范围
(1)
(2)
(3)
17.(1)当x为何整数时,分式的值为正整数?
(2)已知函数自变量取值范围为整数,求y的最大、最小值.
18.如图,用长为20m的篱笆(粗线部分)和墙围成一块菜地,四边形ABCG和四边形DEFG均是正方形,在边DE处有2米宽的入口MN(此处安装简易门).设 (m), (m).
(1)求y与x间的关系式.
(2)若菜地面积为S(m2),求S与x间的关系式.
19.如图,在矩形ABCD中,对角线AC和BD相交于点O,若∠AOB=60°,AD=8,M是线段AD上的一个动点(不与端点A、D重合),MF⊥BD,ME⊥AC,垂足分别为点F、E.
(1)求AB的长;
(2)设ME=x,MF=y,求y关于x的函数关系式
20.如果有一个四位数,百位比千位大1,个位比十位大1,那么我们把这个四位数称为“阶梯数”,把的千位和十位对调,把百位和个位对调得到的数为,并规定
.比如1256,且,1256为“阶梯数”,
,再比如1246,,1246不是“阶梯数”.
(1)判断3467和2368是不是“阶梯数”,并说明理由,如果是“阶梯数”的请求出其的值;
(2)已知,(,,,)且和都是“阶梯数”,是一个完全平方数,能被11整除,求的值.
21.如图所示,在中,底边,高,E为上一动点,当点E从点D向点A运动时,的面积发生了变化.
(1)若设长为,的面积为y,求y与x之间的关系式及x的范围.
(2)当长度为时,的面积y是多少?
22.为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下,制成表格:
汽车行驶的时间t(小时) 0 1 2 3 …
油箱中的剩余油量Q(升) 100 94 88 82 …
(1)如表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据表可知,该车油箱的大小为 升,每小时耗油 升;
(3)两个变量Q与t之间的关系式为 .
23.如果3个数位相同的自然数,,满足:,且各数位上的数字全部相同,则称数和数是一对“黄金搭档数”.例如:因为123,765,888都是三位数,,所以123和是一对“黄金搭档数”.再如:因为26,29,55都是两位数,,所以26和29是一对“黄金搭档数”.
(1)若326与一个个位上的数字是3的数是一对“黄金搭档数”,389与一个个位上的数字是8的数是一对“黄金搭档数”,直接写出和的值;
(2)若,,且,和是一对“黄金搭档数”,求这样的“黄金搭档数”一共有多少对
【参考答案】
1.B 2.D 3.C 4.C 5.D 6.B 7.C 8.D 9.C 10.C
11.1≤x≤2
12.
13.
14.或
15.1
16.(1)且;(2)且;(3)
17.(1);(2)y最大为3,最小为1
18.(1);(2)S
19.(1);(2)()
20.(1)3467为“阶梯数”;2368不是“阶梯数”,;(2)的值为5746或9046.
21.(1)y=4x,0≤x≤6;(2)12cm2.
22.(1)汽车行驶时间t;汽车油箱的剩余油量Q;(2)100,6;(3)Q=100-t
23.(1);(2)对.
