2022年人教版七年级数学下册 5.1.3 同位角、内错角、同旁内角 课件(26张)
文档属性
| 名称 | 2022年人教版七年级数学下册 5.1.3 同位角、内错角、同旁内角 课件(26张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 11:58:26 | ||
图片预览

文档简介
(共26张PPT)
第五章 相交线与平行线
5.1 相交线
5.1.3 同位角、内错角、同旁内角
导入新课
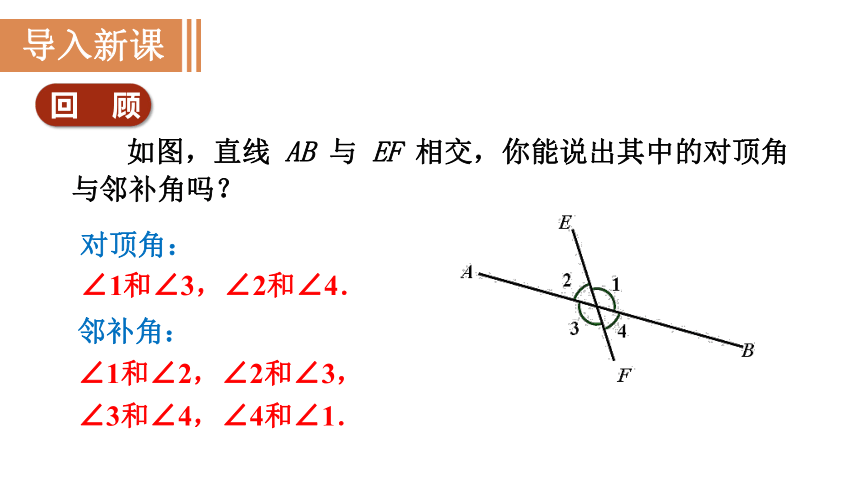
如图,直线 AB 与 EF 相交,你能说出其中的对顶角与邻补角吗?
对顶角:
∠1和∠3,∠2和∠4.
邻补角:
∠1和∠2,∠2和∠3,
∠3和∠4,∠4和∠1.
回顾
探究新知
探 究
三条直线相交可以分为哪些情况?
对三条直线相交按交点的个数分为三种情况:
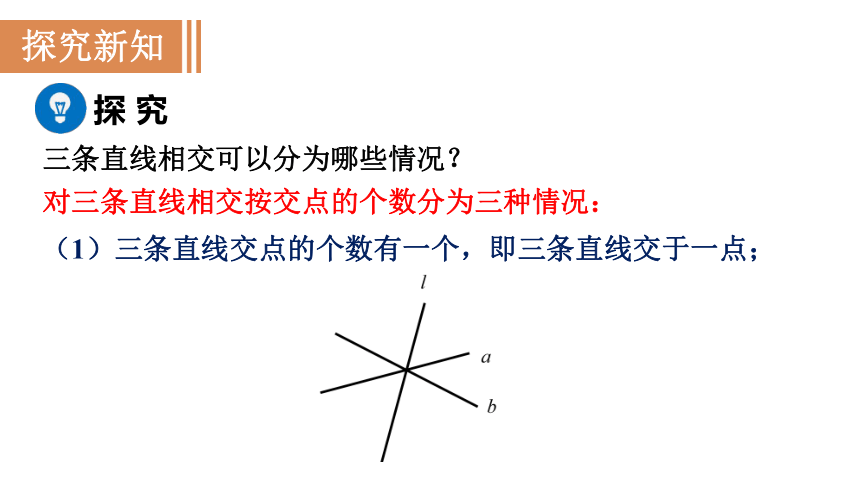
(1)三条直线交点的个数有一个,即三条直线交于一点;
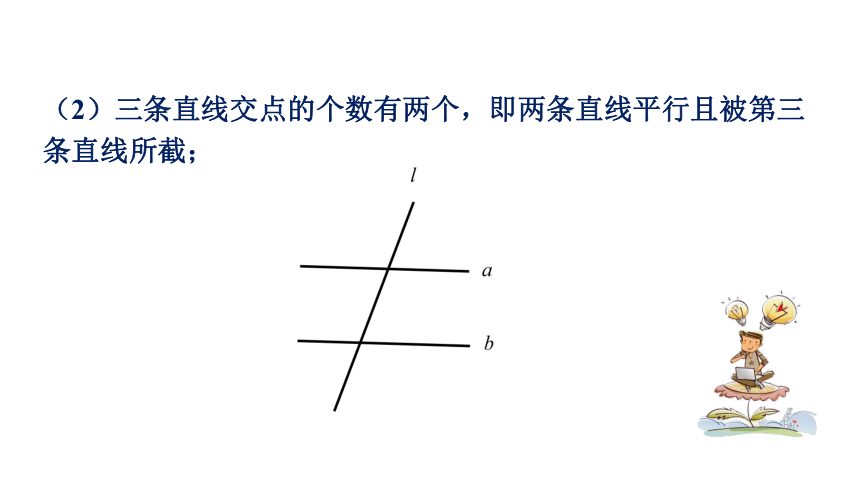
(2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;
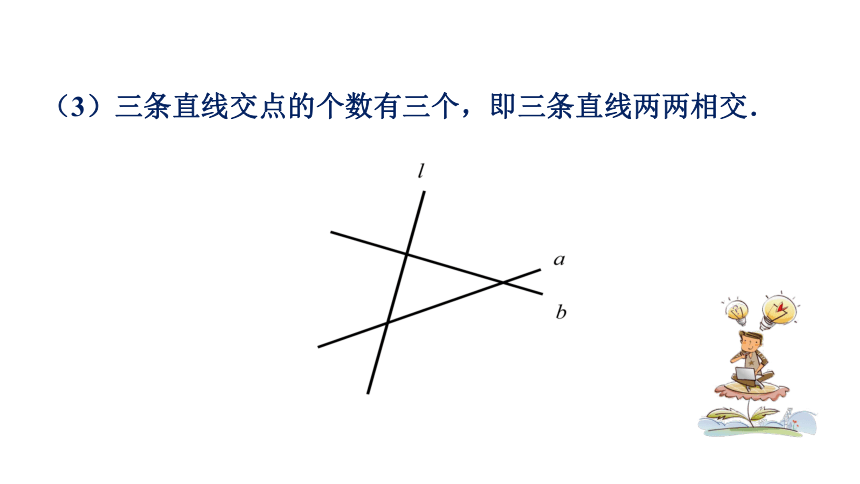
(3)三条直线交点的个数有三个,即三条直线两两相交.
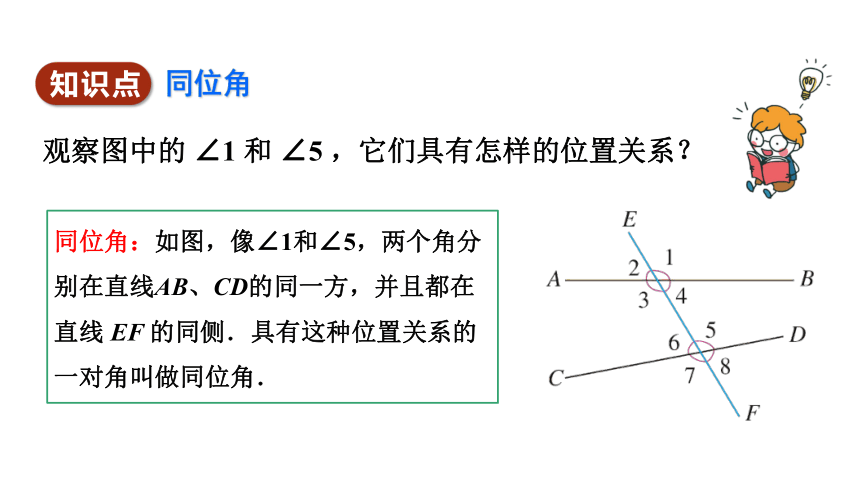
观察图中的 ∠1 和 ∠5 ,它们具有怎样的位置关系?
同位角:如图,像∠1和∠5,两个角分别在直线AB、CD的同一方,并且都在直线 EF 的同侧.具有这种位置关系的一对角叫做同位角.
知识点
同位角
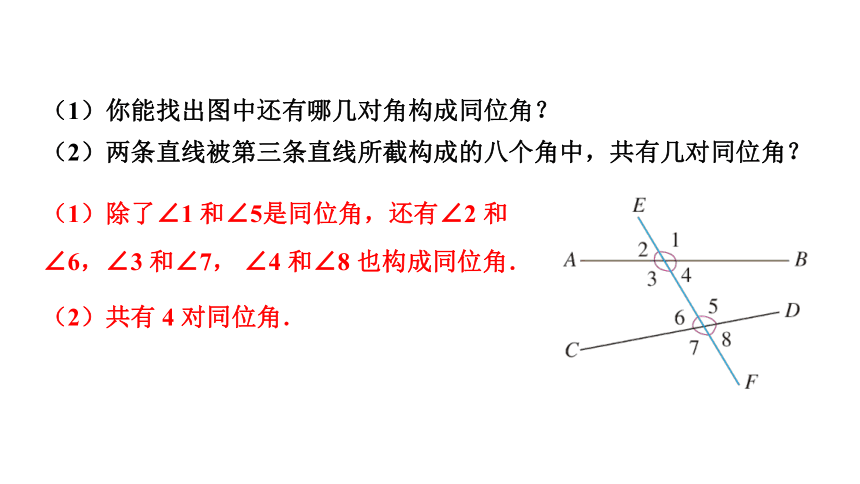
(1)你能找出图中还有哪几对角构成同位角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同位角?
(1)除了∠1 和∠5是同位角,还有∠2 和∠6,∠3 和∠7, ∠4 和∠8 也构成同位角.
(2)共有 4 对同位角.
知识点
内错角
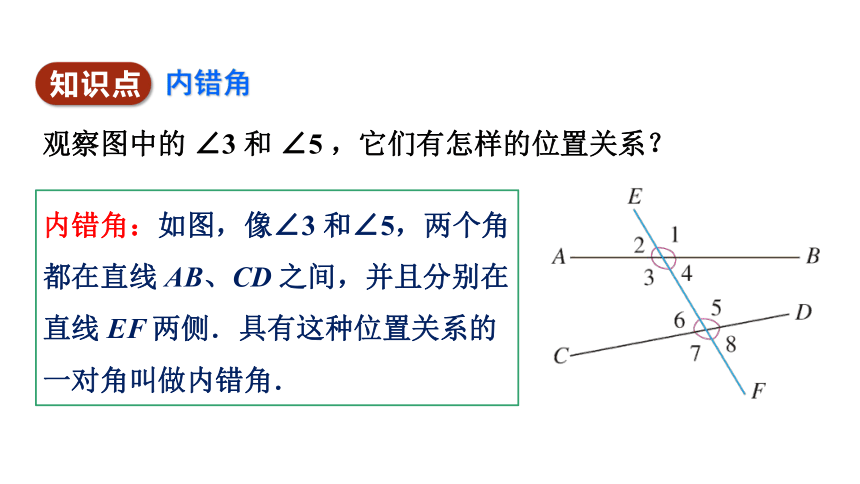
观察图中的 ∠3 和 ∠5 ,它们有怎样的位置关系?
内错角:如图,像∠3 和∠5,两个角都在直线 AB、CD 之间,并且分别在直线 EF 两侧.具有这种位置关系的一对角叫做内错角.
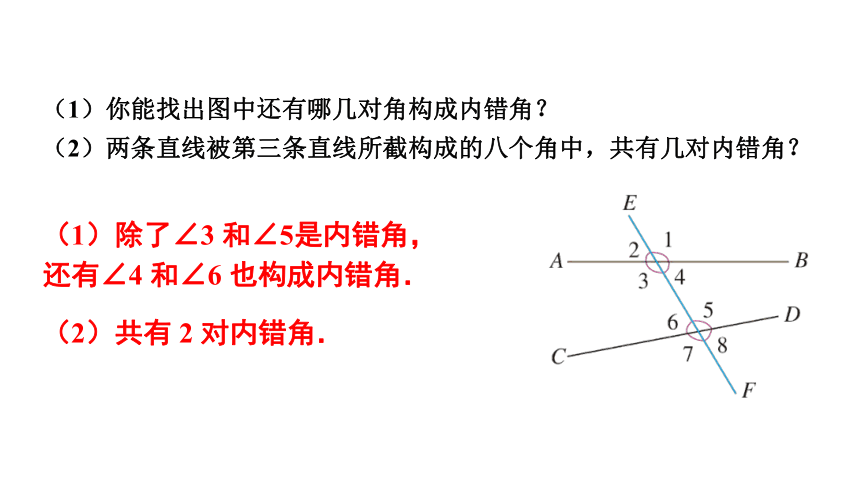
(1)你能找出图中还有哪几对角构成内错角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对内错角?
(1)除了∠3 和∠5是内错角,还有∠4 和∠6 也构成内错角.
(2)共有 2 对内错角.
知识点
同旁内角
如图,我们称∠3 和∠6 为同旁内角,你能根据两个角的特征,描述一下同旁内角的定义吗?
同旁内角:如图,像∠3和∠6,两个角都在直线AB、CD 之间,并且都在直线 EF 的同一旁.具有这种位置关系的一对角叫做同旁内角.
(1)你能找出图中还有哪几对角构成同旁内角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同旁内角?
(1)除了∠3 和∠6是同旁内角,还有∠4 和∠5 也构成同旁内角.
(2)共有 2 对同旁内角.
知识归纳
如图,直线AB,CD与EF相交,∠1和∠5这两个角分别在直线AB,CD的同一方(上方),并且都在直线EF的同侧(右侧),具有这种位置关系的一对角叫做________,像这样的角还有___________,_________,__________.
同位角
∠2与∠6
∠3与∠7
∠4与∠8
如图,∠3和∠5这两个角都在直线AB,CD之间,并且分别在直线EF两侧,具有这种位置关系的一对角叫做________,像这样的角还有___________.
内错角
∠4与∠6
如图,∠3和∠6这两个角都在直线AB,CD之间,但它们都在直线EF的同侧(左侧),具有这种位置关系的一对角叫做___________,像这样的角还有____________.
同旁内角
∠4与∠5
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
例题与练习
如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
4
3
2
1
E
D
C
B
A
解:(1)∠1与∠2是内错角,
∠1和∠3同旁内角,∠1和∠4是同旁内角.
(2)如果∠1=∠4,那么∠1与∠2相等吗?
∠1与∠3互补吗? 为什么?
解:(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那么∠1=∠2.
因为∠3和∠4互补,即∠4+∠3=180°,
又因为∠1=∠4,所以∠4+∠3=180°,即∠1与∠3互补.
如图,根据图形填空:
(1)∠1和∠2是直线________被直线____所截形成的_____角;
(2)∠1和∠3是直线________被直线_____所截形成的_____角;
(3)∠1和∠4是直线________被直线_____所截形成的_______角.
AB,CD
EF
内错
EF,EG
CD
同位
EF,EG
CD
同旁内
归纳:要判断同位角、内错角或同旁内角是由哪两条直线被第三条直线所截形成的,可先判断出第三条直线,第三条直线的显著特点是两个角的公共边.
如图,直线DE截AB,AC,指出图中所有的同位角、内错角、同旁内角.
解:同位角:∠2与∠5,∠4与∠7,∠1与∠8,∠3与∠6,
∠4与∠A,∠8与∠A;
内错角:∠4与∠5,∠3与∠8,∠6与∠A,∠2与∠A;
同旁内角:∠3与∠5,∠4与∠8,∠5与∠A,∠3与∠A.
例题与练习
练习
1.分别指出下列图中的同位角、内错角、同旁内角.
同位角:∠2 与∠6,∠4 与∠8,∠3 与∠7,∠1 与∠5
内错角:∠3 与∠6,∠4 与∠5
同旁内角:∠3 与∠5,∠4 与∠6
同位角:∠1 与∠3,∠2 与∠4
内错角:无
同旁内角:∠2 与 ∠3
2. 如图,∠B 与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C 进行同样的讨论.
解:∠B 与∠DAB 是内错
角,与∠BAE 是同旁内角,它
们都是由 DE 与 BC 被 AB 所截
形成的,还与∠BAC 是同旁内
角,它们是由 AC、BC 被 BA 所截形成的. ∠C 与∠EAC 是内错角,与∠DAC 是同旁内角,它们都是由 DE 与 BC 被 AC 所截形成的. 还与∠BAC 是同旁内角,它们是由 AB、BC 被 AC 所截形成的.
3.下列图形中,∠1和∠2是同位角的是( )
① ② ③ ④ ⑤
A.①②③ B.②③④ C.③④⑤ D.①②⑤
D
4.如图,AB与BC被AD所截得的内错角是__________;DE与AC被直线AD所截得的内错角是__________;图中∠4的内错角是__________.
∠1与∠3
∠2与∠4
∠5和∠2
4.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠3是∠2的内错角.
(1)画出示意图;
(2)若∠1=3∠2,∠2=3∠3,求∠1,∠2的度数.
解:(1)如图;
(2)∵∠1=3∠2,∠2=3∠3,∴∠1=9∠3.
又∵∠1+∠3=9∠3+∠3=180°,
∴∠3=18°,∴∠1=162°,∠2=54°.
课堂小结
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的
第五章 相交线与平行线
5.1 相交线
5.1.3 同位角、内错角、同旁内角
导入新课
如图,直线 AB 与 EF 相交,你能说出其中的对顶角与邻补角吗?
对顶角:
∠1和∠3,∠2和∠4.
邻补角:
∠1和∠2,∠2和∠3,
∠3和∠4,∠4和∠1.
回顾
探究新知
探 究
三条直线相交可以分为哪些情况?
对三条直线相交按交点的个数分为三种情况:
(1)三条直线交点的个数有一个,即三条直线交于一点;
(2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;
(3)三条直线交点的个数有三个,即三条直线两两相交.
观察图中的 ∠1 和 ∠5 ,它们具有怎样的位置关系?
同位角:如图,像∠1和∠5,两个角分别在直线AB、CD的同一方,并且都在直线 EF 的同侧.具有这种位置关系的一对角叫做同位角.
知识点
同位角
(1)你能找出图中还有哪几对角构成同位角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同位角?
(1)除了∠1 和∠5是同位角,还有∠2 和∠6,∠3 和∠7, ∠4 和∠8 也构成同位角.
(2)共有 4 对同位角.
知识点
内错角
观察图中的 ∠3 和 ∠5 ,它们有怎样的位置关系?
内错角:如图,像∠3 和∠5,两个角都在直线 AB、CD 之间,并且分别在直线 EF 两侧.具有这种位置关系的一对角叫做内错角.
(1)你能找出图中还有哪几对角构成内错角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对内错角?
(1)除了∠3 和∠5是内错角,还有∠4 和∠6 也构成内错角.
(2)共有 2 对内错角.
知识点
同旁内角
如图,我们称∠3 和∠6 为同旁内角,你能根据两个角的特征,描述一下同旁内角的定义吗?
同旁内角:如图,像∠3和∠6,两个角都在直线AB、CD 之间,并且都在直线 EF 的同一旁.具有这种位置关系的一对角叫做同旁内角.
(1)你能找出图中还有哪几对角构成同旁内角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同旁内角?
(1)除了∠3 和∠6是同旁内角,还有∠4 和∠5 也构成同旁内角.
(2)共有 2 对同旁内角.
知识归纳
如图,直线AB,CD与EF相交,∠1和∠5这两个角分别在直线AB,CD的同一方(上方),并且都在直线EF的同侧(右侧),具有这种位置关系的一对角叫做________,像这样的角还有___________,_________,__________.
同位角
∠2与∠6
∠3与∠7
∠4与∠8
如图,∠3和∠5这两个角都在直线AB,CD之间,并且分别在直线EF两侧,具有这种位置关系的一对角叫做________,像这样的角还有___________.
内错角
∠4与∠6
如图,∠3和∠6这两个角都在直线AB,CD之间,但它们都在直线EF的同侧(左侧),具有这种位置关系的一对角叫做___________,像这样的角还有____________.
同旁内角
∠4与∠5
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
例题与练习
如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
4
3
2
1
E
D
C
B
A
解:(1)∠1与∠2是内错角,
∠1和∠3同旁内角,∠1和∠4是同旁内角.
(2)如果∠1=∠4,那么∠1与∠2相等吗?
∠1与∠3互补吗? 为什么?
解:(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那么∠1=∠2.
因为∠3和∠4互补,即∠4+∠3=180°,
又因为∠1=∠4,所以∠4+∠3=180°,即∠1与∠3互补.
如图,根据图形填空:
(1)∠1和∠2是直线________被直线____所截形成的_____角;
(2)∠1和∠3是直线________被直线_____所截形成的_____角;
(3)∠1和∠4是直线________被直线_____所截形成的_______角.
AB,CD
EF
内错
EF,EG
CD
同位
EF,EG
CD
同旁内
归纳:要判断同位角、内错角或同旁内角是由哪两条直线被第三条直线所截形成的,可先判断出第三条直线,第三条直线的显著特点是两个角的公共边.
如图,直线DE截AB,AC,指出图中所有的同位角、内错角、同旁内角.
解:同位角:∠2与∠5,∠4与∠7,∠1与∠8,∠3与∠6,
∠4与∠A,∠8与∠A;
内错角:∠4与∠5,∠3与∠8,∠6与∠A,∠2与∠A;
同旁内角:∠3与∠5,∠4与∠8,∠5与∠A,∠3与∠A.
例题与练习
练习
1.分别指出下列图中的同位角、内错角、同旁内角.
同位角:∠2 与∠6,∠4 与∠8,∠3 与∠7,∠1 与∠5
内错角:∠3 与∠6,∠4 与∠5
同旁内角:∠3 与∠5,∠4 与∠6
同位角:∠1 与∠3,∠2 与∠4
内错角:无
同旁内角:∠2 与 ∠3
2. 如图,∠B 与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C 进行同样的讨论.
解:∠B 与∠DAB 是内错
角,与∠BAE 是同旁内角,它
们都是由 DE 与 BC 被 AB 所截
形成的,还与∠BAC 是同旁内
角,它们是由 AC、BC 被 BA 所截形成的. ∠C 与∠EAC 是内错角,与∠DAC 是同旁内角,它们都是由 DE 与 BC 被 AC 所截形成的. 还与∠BAC 是同旁内角,它们是由 AB、BC 被 AC 所截形成的.
3.下列图形中,∠1和∠2是同位角的是( )
① ② ③ ④ ⑤
A.①②③ B.②③④ C.③④⑤ D.①②⑤
D
4.如图,AB与BC被AD所截得的内错角是__________;DE与AC被直线AD所截得的内错角是__________;图中∠4的内错角是__________.
∠1与∠3
∠2与∠4
∠5和∠2
4.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠3是∠2的内错角.
(1)画出示意图;
(2)若∠1=3∠2,∠2=3∠3,求∠1,∠2的度数.
解:(1)如图;
(2)∵∠1=3∠2,∠2=3∠3,∴∠1=9∠3.
又∵∠1+∠3=9∠3+∠3=180°,
∴∠3=18°,∴∠1=162°,∠2=54°.
课堂小结
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的
