2022年人教版七年级数学下册 5.4平移 课件(16张)
文档属性
| 名称 | 2022年人教版七年级数学下册 5.4平移 课件(16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 12:03:13 | ||
图片预览



文档简介
(共16张PPT)
第五章 相交线与平行线
5.4 平移
导入新课
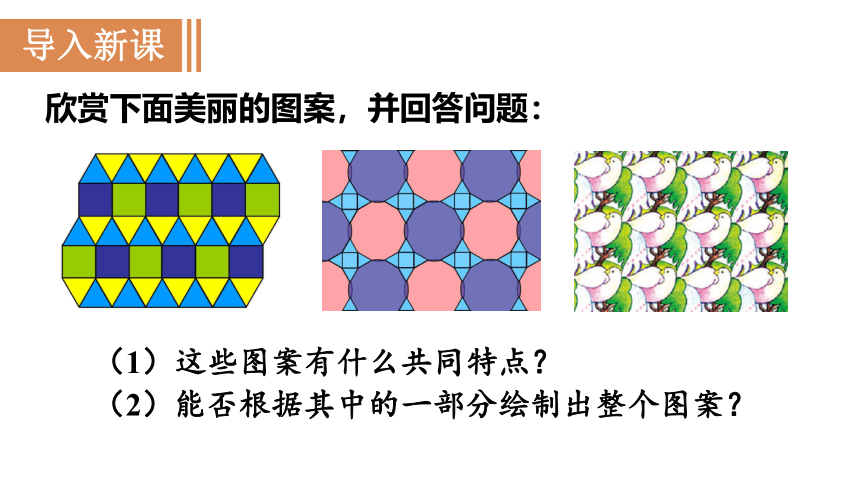
欣赏下面美丽的图案,并回答问题:
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分绘制出整个图案?
探究新知
探究
如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
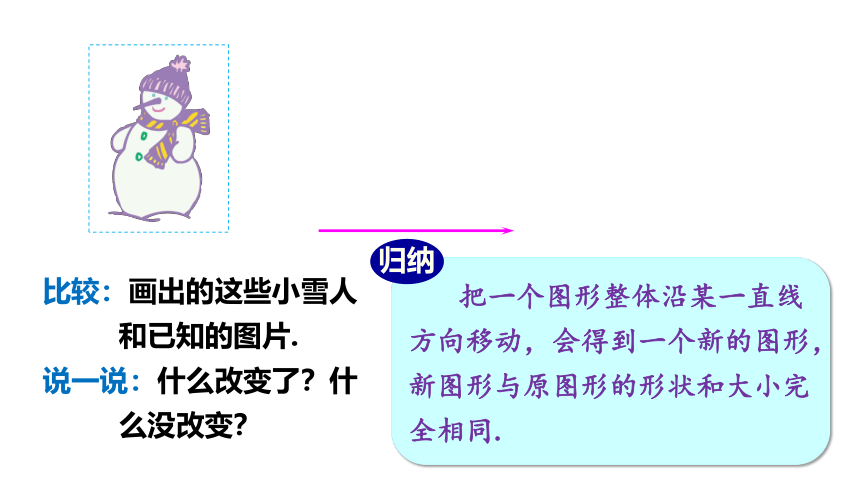
比较:画出的这些小雪人和已知的图片.
说一说:什么改变了?什么没改变?
把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
归纳
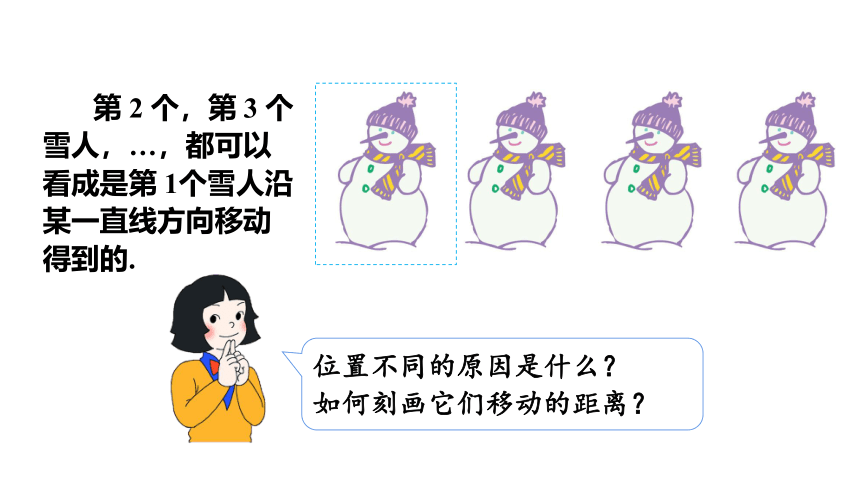
第 2 个,第 3 个雪人,…,都可以看成是第 1个雪人沿某一直线方向移动得到的.
位置不同的原因是什么?
如何刻画它们移动的距离?
探究新知
思考
如下图,在所画的相邻两个雪人中,找出三组对应点.
A
A
'
B
C
B
'
C
'
鼻尖 A 与 A′ 叫做对应点,同样,帽顶 B 与B′,纽扣 C 与 C' 都是对应点.
你能在图中再找出几对对应点吗?
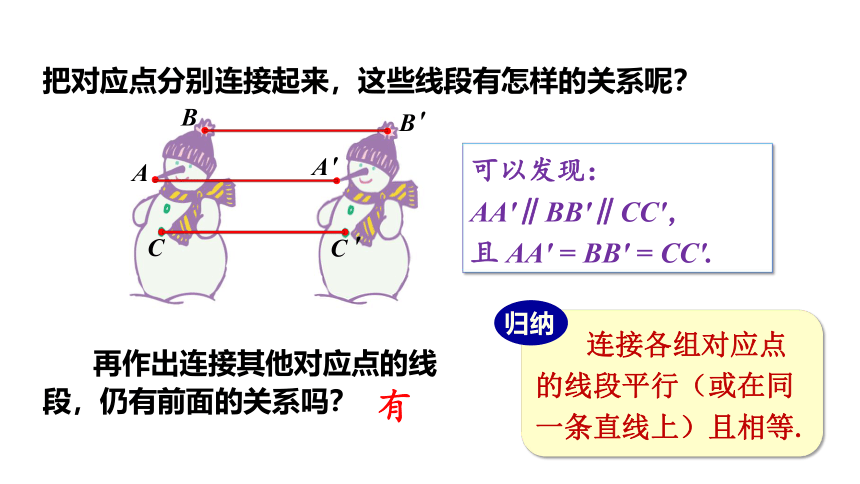
把对应点分别连接起来,这些线段有怎样的关系呢?
可以发现:
AA′∥BB′∥CC′,
且 AA′ = BB′ = CC′.
再作出连接其他对应点的线段,仍有前面的关系吗?
A
A
'
B
C
B
'
C
'
有
连接各组对应点的线段平行(或在同一条直线上)且相等.
归纳
知识归纳
图形的这种移动,叫做平移(translation).
A
A
'
B
C
B
'
C
'
图形的平移不一定是水平的,也不一定是竖直的.
例题与练习
例1 如图,平移△ABC,使点 A 移动到点 A',画出平移后的△A'B'C'.
A
B
C
A′
解:如图,连接 AA′ ,过点 B 作 AA′ 的平行线 l,在 l 上截取 BB′ = AA′,则点 B′ 就是点 B 的对应点.
类似地,作出点 C 的对应点 C' ,得到平移后的△A'B'C'.
l
B′
C′
例2 下列现象:①水平运输带输送物体;②高楼电梯上上下下迎送宾客;③教室的门打开或关上;④教室铝合金窗户的滑动;⑤游乐园里过山车的运动;⑥急刹车时小汽车在地面上的运动.其中属于平移的是____________.(填序号)
①②④⑥
例3 如图,△ABC经过平移得到△A′B′C′,若AB=6,CC′=12,∠BAC=75°,∠ACB=70°.
(1)求∠A′B′C′的度数;
(2)求线段A′B′,BB′的长度.
解:(1)由平移性质,
得∠A′B′C′=∠ABC=180°-∠BAC-∠ACB
=180°-75°-70°=35°;
(2)A′B′=AB=6,BB′=CC′=12.
例题与练习
练习
1.下列哪个图形是由左图平移得到的( )
C
2.如图,△A′B′C′是由△ABC向右平移4 cm得到的,已知∠BAC=80°,∠ACB=30°,A′B′=5 cm,B′C=3 cm,则∠C′=______,∠1=______,AB=____cm,B′C′=____cm,AA′=____cm.
30°
100°
5
7
4
3.完成下列平移图形:
(1)如图①,平移等边三角形ABC,平移方向是由P到Q,平移距离为△ABC的边长;
(2)如图②,将网格中的四边形ABCD向左平移4格,再向上平移2格.
图① 图②
解:(1)(2)如图所示.
A
B
C
B
P
Q
A′
C′
B′
A
C
D
A′
C′
B′
D′
课堂小结
1.关键在于按要求作出对应点;
2.然后,顺次连接对应点即可.
1.平移前后图形的形状和大小完全相同;
2.对应线段平行(或在同一直线 上)且相等;
平移的概念
平移的性质
平移作图
平移
3.各对应点所连线段平行(或在同一直线上)且相等.
第五章 相交线与平行线
5.4 平移
导入新课
欣赏下面美丽的图案,并回答问题:
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分绘制出整个图案?
探究新知
探究
如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
比较:画出的这些小雪人和已知的图片.
说一说:什么改变了?什么没改变?
把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
归纳
第 2 个,第 3 个雪人,…,都可以看成是第 1个雪人沿某一直线方向移动得到的.
位置不同的原因是什么?
如何刻画它们移动的距离?
探究新知
思考
如下图,在所画的相邻两个雪人中,找出三组对应点.
A
A
'
B
C
B
'
C
'
鼻尖 A 与 A′ 叫做对应点,同样,帽顶 B 与B′,纽扣 C 与 C' 都是对应点.
你能在图中再找出几对对应点吗?
把对应点分别连接起来,这些线段有怎样的关系呢?
可以发现:
AA′∥BB′∥CC′,
且 AA′ = BB′ = CC′.
再作出连接其他对应点的线段,仍有前面的关系吗?
A
A
'
B
C
B
'
C
'
有
连接各组对应点的线段平行(或在同一条直线上)且相等.
归纳
知识归纳
图形的这种移动,叫做平移(translation).
A
A
'
B
C
B
'
C
'
图形的平移不一定是水平的,也不一定是竖直的.
例题与练习
例1 如图,平移△ABC,使点 A 移动到点 A',画出平移后的△A'B'C'.
A
B
C
A′
解:如图,连接 AA′ ,过点 B 作 AA′ 的平行线 l,在 l 上截取 BB′ = AA′,则点 B′ 就是点 B 的对应点.
类似地,作出点 C 的对应点 C' ,得到平移后的△A'B'C'.
l
B′
C′
例2 下列现象:①水平运输带输送物体;②高楼电梯上上下下迎送宾客;③教室的门打开或关上;④教室铝合金窗户的滑动;⑤游乐园里过山车的运动;⑥急刹车时小汽车在地面上的运动.其中属于平移的是____________.(填序号)
①②④⑥
例3 如图,△ABC经过平移得到△A′B′C′,若AB=6,CC′=12,∠BAC=75°,∠ACB=70°.
(1)求∠A′B′C′的度数;
(2)求线段A′B′,BB′的长度.
解:(1)由平移性质,
得∠A′B′C′=∠ABC=180°-∠BAC-∠ACB
=180°-75°-70°=35°;
(2)A′B′=AB=6,BB′=CC′=12.
例题与练习
练习
1.下列哪个图形是由左图平移得到的( )
C
2.如图,△A′B′C′是由△ABC向右平移4 cm得到的,已知∠BAC=80°,∠ACB=30°,A′B′=5 cm,B′C=3 cm,则∠C′=______,∠1=______,AB=____cm,B′C′=____cm,AA′=____cm.
30°
100°
5
7
4
3.完成下列平移图形:
(1)如图①,平移等边三角形ABC,平移方向是由P到Q,平移距离为△ABC的边长;
(2)如图②,将网格中的四边形ABCD向左平移4格,再向上平移2格.
图① 图②
解:(1)(2)如图所示.
A
B
C
B
P
Q
A′
C′
B′
A
C
D
A′
C′
B′
D′
课堂小结
1.关键在于按要求作出对应点;
2.然后,顺次连接对应点即可.
1.平移前后图形的形状和大小完全相同;
2.对应线段平行(或在同一直线 上)且相等;
平移的概念
平移的性质
平移作图
平移
3.各对应点所连线段平行(或在同一直线上)且相等.
