2022年人教版七年级数学下册 6.3.1 实数的概念 课件(第一课时 24张)
文档属性
| 名称 | 2022年人教版七年级数学下册 6.3.1 实数的概念 课件(第一课时 24张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 12:05:32 | ||
图片预览







文档简介
(共24张PPT)
第六章 实数
6.3 实数
第1课时 实数的概念
导入新课
交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度,所用的经验公式是v=16 ,其中v表示车速(单位:km/h),d表示刹车后车
轮滑过的距离(单位:m),f 表
示摩擦因数.在一次交通事故
调查中,测得d=20 m,f=1.2.
肇事汽车v=16× =
16 .
思考
对数 提出如下问题:
(1)可能是整数吗?
(2)可能是分数吗?
(3)如果既不是整数又不是分数,
那么究竟是什么数呢?
= 2.5
= – 0.6
= 6.75
= 1.2
·
1. 我们知道有理数包括整数和分数,请把下列分数写成小数的形式,你有什么发现?
= 0.81
·
·
这些分数都可以写成有限小数或者无限循环小数的形式.
探究新知
探究
2. 整数能写成小数的形式,比如 3 可以看成是 3.0 .
由此可以得到结论:
①有理数都可以化成有限小数或无限循环小数的形式;
②反过来,任何有限小数或无限循环小数也都是有理数.
3. 所有的数都可以写成有限小数和无限循环小数的形式吗?
不是. 如:π = 3.1415926535897932384626…
= 1.4142135623730950488016…
无理数和实数的概念
知识归纳
(1) 无限不循环小数叫做无理数.
(2) 有理数和无理数统称为实数.
(3) 实数的两种分类:
实数
正实数
0
负实数
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
思考
是无理数吗?2.020 020 002 000 02…是无理数吗?
= 1.570 796 326 794 89… ,2.020 020 002 000 02… ,
它们都是无限不循环小数,是无理数.
常见的一些无理数:
(1)含 π 的一些数;
(2)开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001…
练一练
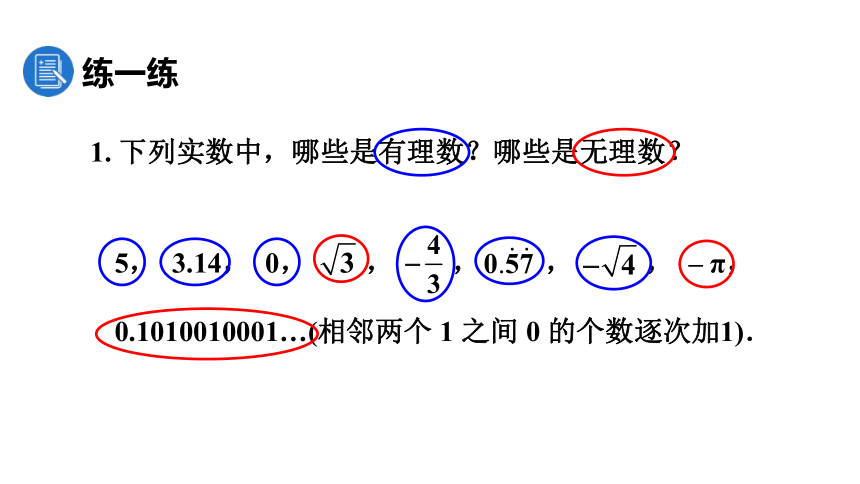
1. 下列实数中,哪些是有理数?哪些是无理数?
5, 3.14, 0, , , , , – π,
0.1010010001…(相邻两个 1 之间 0 的个数逐次加1).
O
1
2
3
4
O'
在数轴上表示实数
探究新知
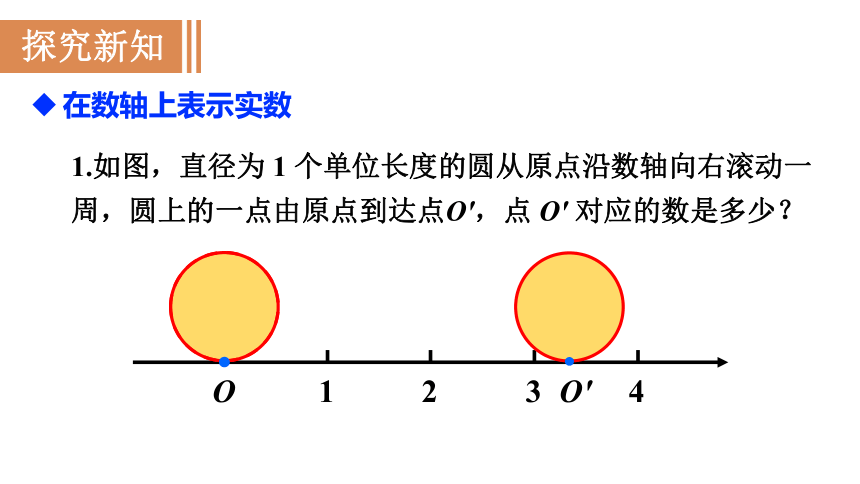
1.如图,直径为 1 个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O′,点 O′ 对应的数是多少?
O
1
2
3
4
O'
从图中可以看出,OO′ 的长是这个圆的周长 π,所以点 O′ 对应的数是 π.这样,无理数 π 可以用数轴上的点表示出来.
0
1
2
3
-1
-2
-3
2.以单位长度为边长画一个正方形,以原点为圆心,正方形的对角线为半径画弧.
弧与正半轴的交点就表示 ,
弧与负半轴的交点就表示 .
小结
事实上,每一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的.
4
-2
0
-1
1
2
3
将图中数轴上标红的各点与下列实数对应起来.
-1.5
π
3
练一练
探究新知
实数的大小比较
● 与有理数一样,实数也可以比较大小.
● 与有理数规定的大小一样,数轴上右边的点表示的实数比
左边的点表示的实数大.
● 与有理数一样,在实数范围内:
①正数大于零,负数小于零,
正数大于负数;
②两个正数,绝对值大的数较大;
③两个负数,绝对值大的数反而小.
原
点
0
正实数
负实数
<
例题与练习
例1 把下列各数填在相应的大括号内:
0, , , , ,-2, , , ,
0.616616661… .
自然数集合 { };
有理数集合 { };
0, ,…
0, , ,-2, ,…
0, , , , ,-2, , , ,
0.616616661… .
无理数集合 { };
正数集合 { };
整数集合 { };
0, ,-2,…
, , , ,0.616616661…,…
, , , , ,0.616616661…,…
0, , , , ,-2, , , ,
0.616616661… .
非负整数集合 { };
0, ,…
分数集合 { };
, ,…
注意: 不是分数,分数的表现形式 (a、b均为整数且a≠0).
例2 如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将该圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )
A.π-1 B.-π-1
C.-π+1 D.π-1或-π-1
例3 若数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
0
5.1
A
B
-3
A
-2
-1
0
D
C
例4 如图,数轴上点 A 和点 B 分别表示-1和 ,点 B 关于点 A 的对称点为 C.求点 C 所表示的实数.
解:∵数轴上A,B两点表示的数分别为-1和 ,
∴点B到点A的距离为1+ ,
则点C到点A的距离也为1+ .
设点C表示的实数为x,则点A到点C的距离为-1-x,
∴-1-x=1+ ,
∴x=-2- ,
∴点C所表示的实数为-2 .
-1
0
A
B
练习
1.判断下列说法是否正确:
(1)有限小数都是有理数; ( )
(2)无限小数都是无理数; ( )
(3)所有有理数都可以用数轴上的点表示,反过来,
数轴上的所有点都表示有理数; ( )
(4)所有实数都可以用数轴上的点表示,反过来,
数轴上的所有点都表示实数. ( )
√
×
×
√
2.下列说法正确的是( )
A.a一定是正实数 B. 是有理数
C. 是有理数 D.数轴上任一点都对应一个有理数
3.如图,表示 的点在数轴上哪两个字母之间( )
A.C与D B.A与B
C.A与C D.B与C
0
1
1.5
2
3
A
B
C
2.5
D
B
A
4.在数轴上画出表示 - -1 的点.
解:以单位长度为边长画一个正方形如图,以 -1 为圆心,正方形的对角线为半径画弧,与负半轴的交点就表示点- -1.
0
-1
-2
-3
1
-4
- -1
解:(1) m-(- )=2,∴m=2- ;
(2) BC=|2-(2- )|= .
5.如图,一只蚂蚁从点 A 沿数轴向右爬 2 个单位长度到达点 B,再爬向点 C 停止,已知点 A 所表示的数为- ,点 C 所表示的数为2,设点 B 所表示的数为 m.
(1)求 m 的值;
(2)求 BC 的长.
-2
-1
0
1
2
A
B
C
课堂小结
实数
无理数和实数的概念
实数的分类
在数轴上表示实数
实数的大小比较
第六章 实数
6.3 实数
第1课时 实数的概念
导入新课
交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度,所用的经验公式是v=16 ,其中v表示车速(单位:km/h),d表示刹车后车
轮滑过的距离(单位:m),f 表
示摩擦因数.在一次交通事故
调查中,测得d=20 m,f=1.2.
肇事汽车v=16× =
16 .
思考
对数 提出如下问题:
(1)可能是整数吗?
(2)可能是分数吗?
(3)如果既不是整数又不是分数,
那么究竟是什么数呢?
= 2.5
= – 0.6
= 6.75
= 1.2
·
1. 我们知道有理数包括整数和分数,请把下列分数写成小数的形式,你有什么发现?
= 0.81
·
·
这些分数都可以写成有限小数或者无限循环小数的形式.
探究新知
探究
2. 整数能写成小数的形式,比如 3 可以看成是 3.0 .
由此可以得到结论:
①有理数都可以化成有限小数或无限循环小数的形式;
②反过来,任何有限小数或无限循环小数也都是有理数.
3. 所有的数都可以写成有限小数和无限循环小数的形式吗?
不是. 如:π = 3.1415926535897932384626…
= 1.4142135623730950488016…
无理数和实数的概念
知识归纳
(1) 无限不循环小数叫做无理数.
(2) 有理数和无理数统称为实数.
(3) 实数的两种分类:
实数
正实数
0
负实数
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
思考
是无理数吗?2.020 020 002 000 02…是无理数吗?
= 1.570 796 326 794 89… ,2.020 020 002 000 02… ,
它们都是无限不循环小数,是无理数.
常见的一些无理数:
(1)含 π 的一些数;
(2)开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001…
练一练
1. 下列实数中,哪些是有理数?哪些是无理数?
5, 3.14, 0, , , , , – π,
0.1010010001…(相邻两个 1 之间 0 的个数逐次加1).
O
1
2
3
4
O'
在数轴上表示实数
探究新知
1.如图,直径为 1 个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O′,点 O′ 对应的数是多少?
O
1
2
3
4
O'
从图中可以看出,OO′ 的长是这个圆的周长 π,所以点 O′ 对应的数是 π.这样,无理数 π 可以用数轴上的点表示出来.
0
1
2
3
-1
-2
-3
2.以单位长度为边长画一个正方形,以原点为圆心,正方形的对角线为半径画弧.
弧与正半轴的交点就表示 ,
弧与负半轴的交点就表示 .
小结
事实上,每一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的.
4
-2
0
-1
1
2
3
将图中数轴上标红的各点与下列实数对应起来.
-1.5
π
3
练一练
探究新知
实数的大小比较
● 与有理数一样,实数也可以比较大小.
● 与有理数规定的大小一样,数轴上右边的点表示的实数比
左边的点表示的实数大.
● 与有理数一样,在实数范围内:
①正数大于零,负数小于零,
正数大于负数;
②两个正数,绝对值大的数较大;
③两个负数,绝对值大的数反而小.
原
点
0
正实数
负实数
<
例题与练习
例1 把下列各数填在相应的大括号内:
0, , , , ,-2, , , ,
0.616616661… .
自然数集合 { };
有理数集合 { };
0, ,…
0, , ,-2, ,…
0, , , , ,-2, , , ,
0.616616661… .
无理数集合 { };
正数集合 { };
整数集合 { };
0, ,-2,…
, , , ,0.616616661…,…
, , , , ,0.616616661…,…
0, , , , ,-2, , , ,
0.616616661… .
非负整数集合 { };
0, ,…
分数集合 { };
, ,…
注意: 不是分数,分数的表现形式 (a、b均为整数且a≠0).
例2 如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将该圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )
A.π-1 B.-π-1
C.-π+1 D.π-1或-π-1
例3 若数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
0
5.1
A
B
-3
A
-2
-1
0
D
C
例4 如图,数轴上点 A 和点 B 分别表示-1和 ,点 B 关于点 A 的对称点为 C.求点 C 所表示的实数.
解:∵数轴上A,B两点表示的数分别为-1和 ,
∴点B到点A的距离为1+ ,
则点C到点A的距离也为1+ .
设点C表示的实数为x,则点A到点C的距离为-1-x,
∴-1-x=1+ ,
∴x=-2- ,
∴点C所表示的实数为-2 .
-1
0
A
B
练习
1.判断下列说法是否正确:
(1)有限小数都是有理数; ( )
(2)无限小数都是无理数; ( )
(3)所有有理数都可以用数轴上的点表示,反过来,
数轴上的所有点都表示有理数; ( )
(4)所有实数都可以用数轴上的点表示,反过来,
数轴上的所有点都表示实数. ( )
√
×
×
√
2.下列说法正确的是( )
A.a一定是正实数 B. 是有理数
C. 是有理数 D.数轴上任一点都对应一个有理数
3.如图,表示 的点在数轴上哪两个字母之间( )
A.C与D B.A与B
C.A与C D.B与C
0
1
1.5
2
3
A
B
C
2.5
D
B
A
4.在数轴上画出表示 - -1 的点.
解:以单位长度为边长画一个正方形如图,以 -1 为圆心,正方形的对角线为半径画弧,与负半轴的交点就表示点- -1.
0
-1
-2
-3
1
-4
- -1
解:(1) m-(- )=2,∴m=2- ;
(2) BC=|2-(2- )|= .
5.如图,一只蚂蚁从点 A 沿数轴向右爬 2 个单位长度到达点 B,再爬向点 C 停止,已知点 A 所表示的数为- ,点 C 所表示的数为2,设点 B 所表示的数为 m.
(1)求 m 的值;
(2)求 BC 的长.
-2
-1
0
1
2
A
B
C
课堂小结
实数
无理数和实数的概念
实数的分类
在数轴上表示实数
实数的大小比较
