2022年人教版七年级数学下册 8.3.2 利用二元一次方程组解决较复杂的实际问题 课件(第二课时 30张)
文档属性
| 名称 | 2022年人教版七年级数学下册 8.3.2 利用二元一次方程组解决较复杂的实际问题 课件(第二课时 30张) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 12:17:09 | ||
图片预览







文档简介
(共30张PPT)
第八章 二元一次方程组
8.1 二元一次方程组
第2课时 利用二元一次方程组解决较复杂的实际问题
导入新课
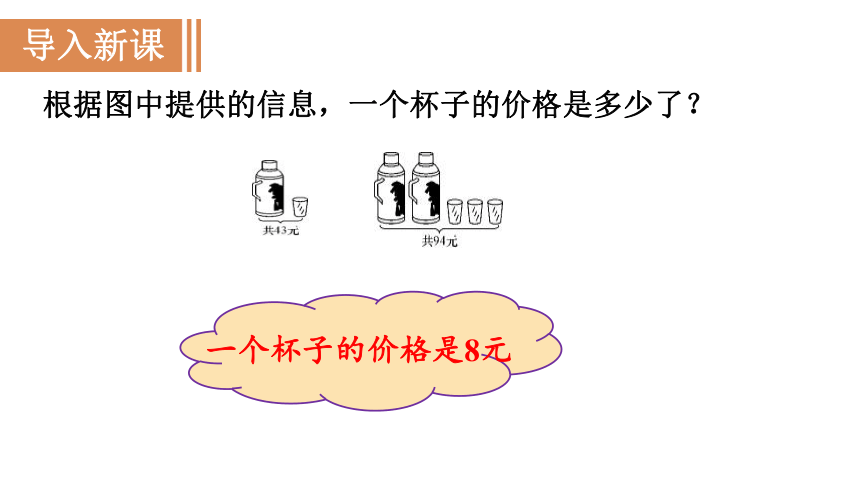
根据图中提供的信息,一个杯子的价格是多少了?
一个杯子的价格是8元
原材料费与原材料数量的关系:
运费与产品重量和路程的关系:
对于较复杂的数量关系:
原材料费=原材料数量×单价
运费=产品重量×1吨/千米的运费×路程.
可以通过列表来理顺关系.
探究新知
据统计资料,甲、乙两种作物的单位面积产量的比是 1:2.现要把一块长 200 m、宽 100 m 的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是 3:4?
几何图形问题
这里研究的实际上是长方形的面积分割问题,可以画出示意图来帮助自己.
把一个长方形分成两个小长方形,有哪些分割方式?
保持宽不变,把长分成两段;
01
保持长不变,把宽分成两段.
02
01
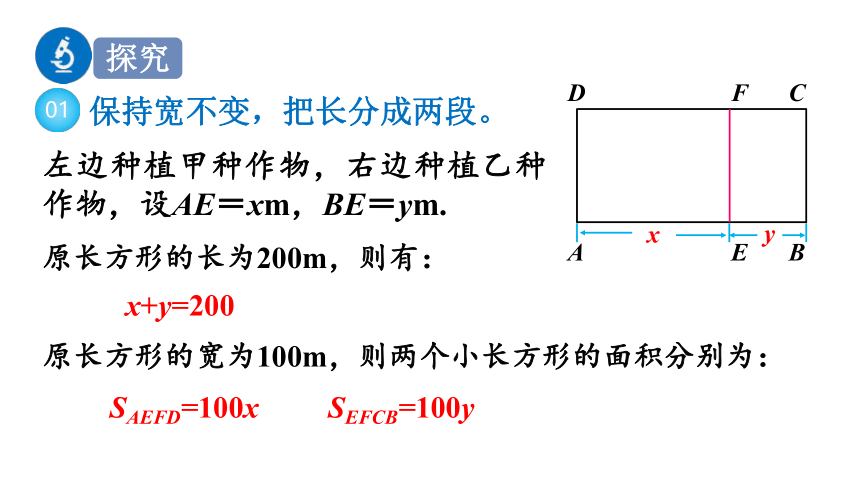
保持宽不变,把长分成两段。
左边种植甲种作物,右边种植乙种作物,设AE=xm,BE=ym.
x
y
原长方形的长为200m,则有:
A
D
C
F
B
E
x+y=200
原长方形的宽为100m,则两个小长方形的面积分别为:
SAEFD=100x
SEFCB=100y
探究
A
D
C
F
x
y
B
E
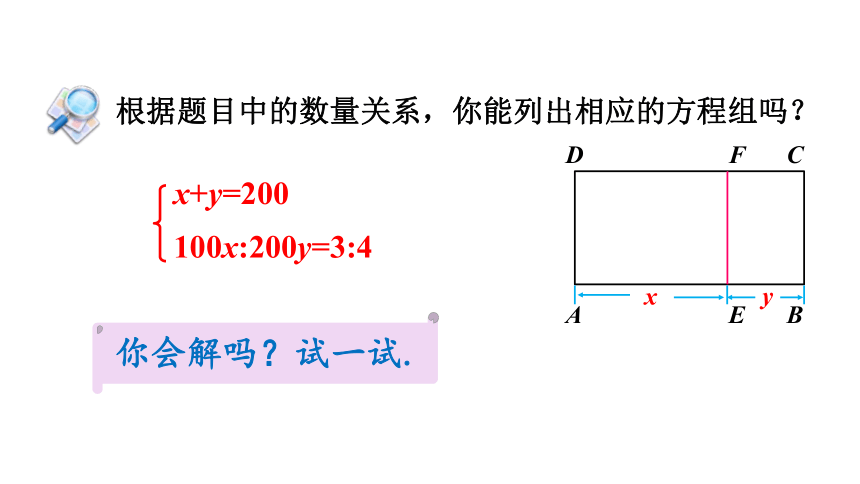
根据题目中的数量关系,你能列出相应的方程组吗?
x+y=200
100x:200y=3:4
你会解吗?试一试.
对②移项并化简得:400x=600y
2x=3y ③
解答
x+y=200
100x:200y=3:4
①
②
方程组
联立①③,解得: .
x=120
y=80
过长方形土地的长边上离左端120m处,作这条边的垂线,把这块土地分为两块长方形土地.左边较大一块土地种甲种作物,右边较小一块土地种乙种作物.
归纳
02
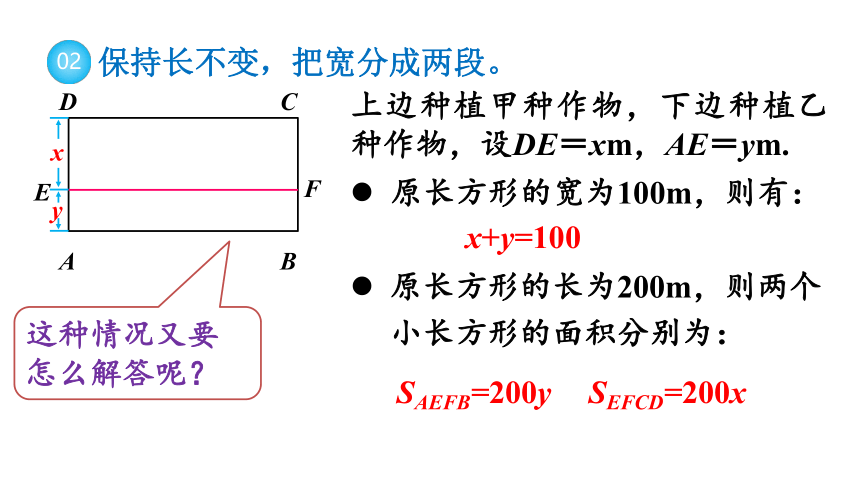
保持长不变,把宽分成两段。
A
D
C
B
x
y
这种情况又要怎么解答呢?
上边种植甲种作物,下边种植乙种作物,设DE=xm,AE=ym.
F
x+y=100
SAEFB=200y
SEFCD=200x
E
原长方形的宽为100m,则有:
原长方形的长为200m,则两个小长方形的面积分别为:
A
D
C
F
x
y
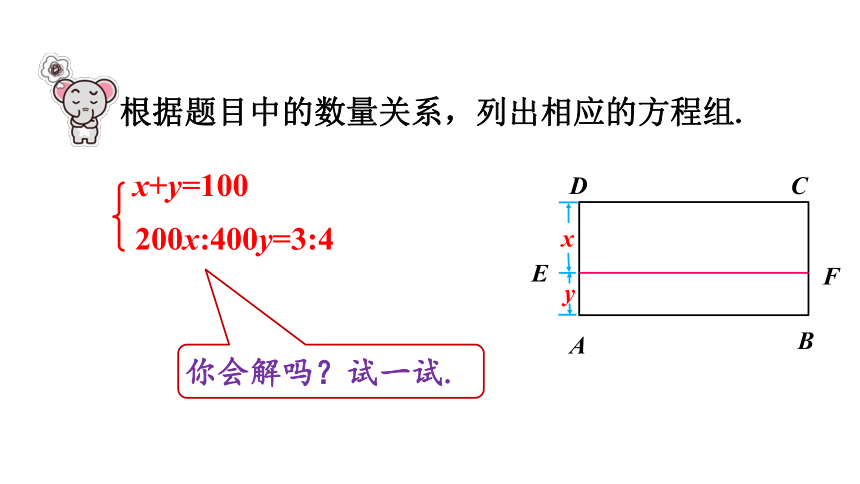
根据题目中的数量关系,列出相应的方程组.
B
E
x+y=100
200x:400y=3:4
你会解吗?试一试.
x+y=100
200x:400y=3:4
①
②
对②移项得:400x=600y
并化简得:2x=3y ③
解答
方程组
联立①③,解得: .
x=60
y=40
过长方形土地的长边上离上端60m处,作这条边的垂线,把这块土地分为两块长方形土地.上边较大一块土地种甲种作物,下边较小一块土地种乙种作物.
归纳
行程问题、工程问题
如图,长青化工厂与 A,B 两地有公路、铁路相连.这家工厂从A地购买一批每吨 1 000元的原料运回工厂,制成每吨 8 000 元的产品运到 B 地.公路运价为 1. 5元/(t·km),铁路运价为 1.2元/(t·km),这两次运输共支出公路运费 15 000 元,铁路运费 97 200 元.这批产品的销售款比原料费与运输费的和多多少元?
问题1 要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们必须知道产品的数量和原料的数量.
销售款
原料费
运输费(公路和铁路)
产品数量
原料数量
问题2 本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.本题涉及哪两类量呢?
一类是公路运费,铁路运费,价值;
另一类是产品数量,原料数量.
问题3 你能完成教材上的表格吗?
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
1.5×20x
1.5×10y
1.5(20x+10y)
1.2×110x
1.2×120y
1.2(110x+120y)
8 000x
1 000y
问题4 你发现等量关系了吗?如何列方程组并求解?
1.5 =15000,
1.2 =97200
×(20x+10y)
×(110x+120y)
解:先化简,得
2x+y=1000
11x+12y=8100
①
②
③
由①,得
y=1000-2x
代入② ,得
11x+12(1000-2x)=8100
x=300
代入③ ,得
y=400
是原方程组的解.
x=300,
y=400
∴
问题5 这个实际问题的答案是什么?
销售款:8 000×300=2 400 000;
原料费:1 000×400=400 000;
运输费:15 000+97 200=112 200.
这批产品的销售款比原料费与运输费的和多1 887 800元.
知识归纳
方程组是解决含有多个 未知数问题的重要工具,用方程组解决问题时,要根据问题中的数量关系列出方程组,求出方程组的解后,应进一步考虑它是否符合问题的实际意义.
例题与练习
例1 小王购买了一套经济适用房,他准备将地面上铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
解:(1)地面总面积为(6x+2y+18)m2;
(1)用含x,y的式子表示地面总面积;
(2)已知客厅面积比卫生间面积多21m2,且地砖总面积是卫生间面积的15倍,铺1m2地砖的平均费用为80元,铺地砖的总费用是多少元?
解:由题意,得
6x-2y=21,
6x+2y+18=15
×2y
∴地面总面积为6×4+2×2 +18=45(m2).
∴铺地砖的总费用为45×80=3600(元).
解得
x=4
y=
例2 某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植作物每公顷所需的劳动力人数及投入的设备资金如下表:
农作物品种 每公顷需劳动力 每公顷需投入的设备资金
水稻 4人 1万元
棉花 8人 1万元
蔬菜 5人 2万元
已知该农场计划投入的设备资金是67万元,应该怎样安排这三种作物的种植面积,才能使所有职工都有工作,而且投入的设备资金正好够用?
解:设安排x公顷种植水稻,y公顷种植棉花,则(51-x-y)公顷种植蔬菜.
根据题意,得
4x+8y+5(51-x-y)=300,
x+y+2(51-x-y)=67
解得
x=15
y=20
那么种植蔬菜的面积为51-15-20=16(公顷).
答:安排15公顷种植水稻,20公顷种植棉花,16公顷种植蔬菜,才能使所有职工都有工作,而且投入的设备资金正好够用.
练习
1.陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )
A.19 B.18 C.16 D.15
C
2.某校九年级(1)班40名同学为灾区捐款,共捐款1000元,捐款情况如下表,则捐款20元的有____人.
捐款(元) 10 20 30 40
人数 6 ? ? 7
15
3.如图,用8块相同的小长方形拼成一个宽为48cm的大长方形,每块小长方形的长和宽分别是多少?
解:设每块小长方形的长是xcm,宽是ycm.
依题意,得x+y=48.(x=3y,)
答:每块小长方形的长是36cm,宽是12cm.
解得y=12.(x=36,)
课堂小结
实际问题与二元一次方程组(3)
工程、行程问题
题目中涉及的量多
列表分析
发现等量关系
列方程求解
第八章 二元一次方程组
8.1 二元一次方程组
第2课时 利用二元一次方程组解决较复杂的实际问题
导入新课
根据图中提供的信息,一个杯子的价格是多少了?
一个杯子的价格是8元
原材料费与原材料数量的关系:
运费与产品重量和路程的关系:
对于较复杂的数量关系:
原材料费=原材料数量×单价
运费=产品重量×1吨/千米的运费×路程.
可以通过列表来理顺关系.
探究新知
据统计资料,甲、乙两种作物的单位面积产量的比是 1:2.现要把一块长 200 m、宽 100 m 的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是 3:4?
几何图形问题
这里研究的实际上是长方形的面积分割问题,可以画出示意图来帮助自己.
把一个长方形分成两个小长方形,有哪些分割方式?
保持宽不变,把长分成两段;
01
保持长不变,把宽分成两段.
02
01
保持宽不变,把长分成两段。
左边种植甲种作物,右边种植乙种作物,设AE=xm,BE=ym.
x
y
原长方形的长为200m,则有:
A
D
C
F
B
E
x+y=200
原长方形的宽为100m,则两个小长方形的面积分别为:
SAEFD=100x
SEFCB=100y
探究
A
D
C
F
x
y
B
E
根据题目中的数量关系,你能列出相应的方程组吗?
x+y=200
100x:200y=3:4
你会解吗?试一试.
对②移项并化简得:400x=600y
2x=3y ③
解答
x+y=200
100x:200y=3:4
①
②
方程组
联立①③,解得: .
x=120
y=80
过长方形土地的长边上离左端120m处,作这条边的垂线,把这块土地分为两块长方形土地.左边较大一块土地种甲种作物,右边较小一块土地种乙种作物.
归纳
02
保持长不变,把宽分成两段。
A
D
C
B
x
y
这种情况又要怎么解答呢?
上边种植甲种作物,下边种植乙种作物,设DE=xm,AE=ym.
F
x+y=100
SAEFB=200y
SEFCD=200x
E
原长方形的宽为100m,则有:
原长方形的长为200m,则两个小长方形的面积分别为:
A
D
C
F
x
y
根据题目中的数量关系,列出相应的方程组.
B
E
x+y=100
200x:400y=3:4
你会解吗?试一试.
x+y=100
200x:400y=3:4
①
②
对②移项得:400x=600y
并化简得:2x=3y ③
解答
方程组
联立①③,解得: .
x=60
y=40
过长方形土地的长边上离上端60m处,作这条边的垂线,把这块土地分为两块长方形土地.上边较大一块土地种甲种作物,下边较小一块土地种乙种作物.
归纳
行程问题、工程问题
如图,长青化工厂与 A,B 两地有公路、铁路相连.这家工厂从A地购买一批每吨 1 000元的原料运回工厂,制成每吨 8 000 元的产品运到 B 地.公路运价为 1. 5元/(t·km),铁路运价为 1.2元/(t·km),这两次运输共支出公路运费 15 000 元,铁路运费 97 200 元.这批产品的销售款比原料费与运输费的和多多少元?
问题1 要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们必须知道产品的数量和原料的数量.
销售款
原料费
运输费(公路和铁路)
产品数量
原料数量
问题2 本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.本题涉及哪两类量呢?
一类是公路运费,铁路运费,价值;
另一类是产品数量,原料数量.
问题3 你能完成教材上的表格吗?
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
1.5×20x
1.5×10y
1.5(20x+10y)
1.2×110x
1.2×120y
1.2(110x+120y)
8 000x
1 000y
问题4 你发现等量关系了吗?如何列方程组并求解?
1.5 =15000,
1.2 =97200
×(20x+10y)
×(110x+120y)
解:先化简,得
2x+y=1000
11x+12y=8100
①
②
③
由①,得
y=1000-2x
代入② ,得
11x+12(1000-2x)=8100
x=300
代入③ ,得
y=400
是原方程组的解.
x=300,
y=400
∴
问题5 这个实际问题的答案是什么?
销售款:8 000×300=2 400 000;
原料费:1 000×400=400 000;
运输费:15 000+97 200=112 200.
这批产品的销售款比原料费与运输费的和多1 887 800元.
知识归纳
方程组是解决含有多个 未知数问题的重要工具,用方程组解决问题时,要根据问题中的数量关系列出方程组,求出方程组的解后,应进一步考虑它是否符合问题的实际意义.
例题与练习
例1 小王购买了一套经济适用房,他准备将地面上铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
解:(1)地面总面积为(6x+2y+18)m2;
(1)用含x,y的式子表示地面总面积;
(2)已知客厅面积比卫生间面积多21m2,且地砖总面积是卫生间面积的15倍,铺1m2地砖的平均费用为80元,铺地砖的总费用是多少元?
解:由题意,得
6x-2y=21,
6x+2y+18=15
×2y
∴地面总面积为6×4+2×2 +18=45(m2).
∴铺地砖的总费用为45×80=3600(元).
解得
x=4
y=
例2 某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植作物每公顷所需的劳动力人数及投入的设备资金如下表:
农作物品种 每公顷需劳动力 每公顷需投入的设备资金
水稻 4人 1万元
棉花 8人 1万元
蔬菜 5人 2万元
已知该农场计划投入的设备资金是67万元,应该怎样安排这三种作物的种植面积,才能使所有职工都有工作,而且投入的设备资金正好够用?
解:设安排x公顷种植水稻,y公顷种植棉花,则(51-x-y)公顷种植蔬菜.
根据题意,得
4x+8y+5(51-x-y)=300,
x+y+2(51-x-y)=67
解得
x=15
y=20
那么种植蔬菜的面积为51-15-20=16(公顷).
答:安排15公顷种植水稻,20公顷种植棉花,16公顷种植蔬菜,才能使所有职工都有工作,而且投入的设备资金正好够用.
练习
1.陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )
A.19 B.18 C.16 D.15
C
2.某校九年级(1)班40名同学为灾区捐款,共捐款1000元,捐款情况如下表,则捐款20元的有____人.
捐款(元) 10 20 30 40
人数 6 ? ? 7
15
3.如图,用8块相同的小长方形拼成一个宽为48cm的大长方形,每块小长方形的长和宽分别是多少?
解:设每块小长方形的长是xcm,宽是ycm.
依题意,得x+y=48.(x=3y,)
答:每块小长方形的长是36cm,宽是12cm.
解得y=12.(x=36,)
课堂小结
实际问题与二元一次方程组(3)
工程、行程问题
题目中涉及的量多
列表分析
发现等量关系
列方程求解
