2021—2022学年人教版九年级数学下册28.1锐角三角函数课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册28.1锐角三角函数课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 244.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 21:23:01 | ||
图片预览



文档简介
2021——2022学年度人教版九年级数学下册 第二十八章 锐角三角函数
28.1锐角三角函数 课后练习
一、选择题
1.如果∠A为锐角,cosA=,那么∠A 取值范围是( )
A.0°<∠A≤30° B.30°<∠A≤45° C.45°<∠A<60° D.60°<∠A<90°
2.已知,则的度数所属范围是( )
A. B.
C. D.
3.如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的正切值( )
A.扩大为原来的两倍 B.缩小为原来的
C.不变 D.不能确定
4.已知某水库大坝的横断面为梯形,其中一斜坡AB的坡度,则斜坡AB的坡角为( )
A.30° B.45° C.60° D.150°
5.如图,在菱形ABCD中,,,,则AB的长为是( )
A.6 B.8 C.10 D.12
6.如图,小明在学校门口的点C处测得树的顶端A仰角为α,同时测得AC=15m,则树的高度AB为( )
A. B.15tanαm C. D.15sinαm
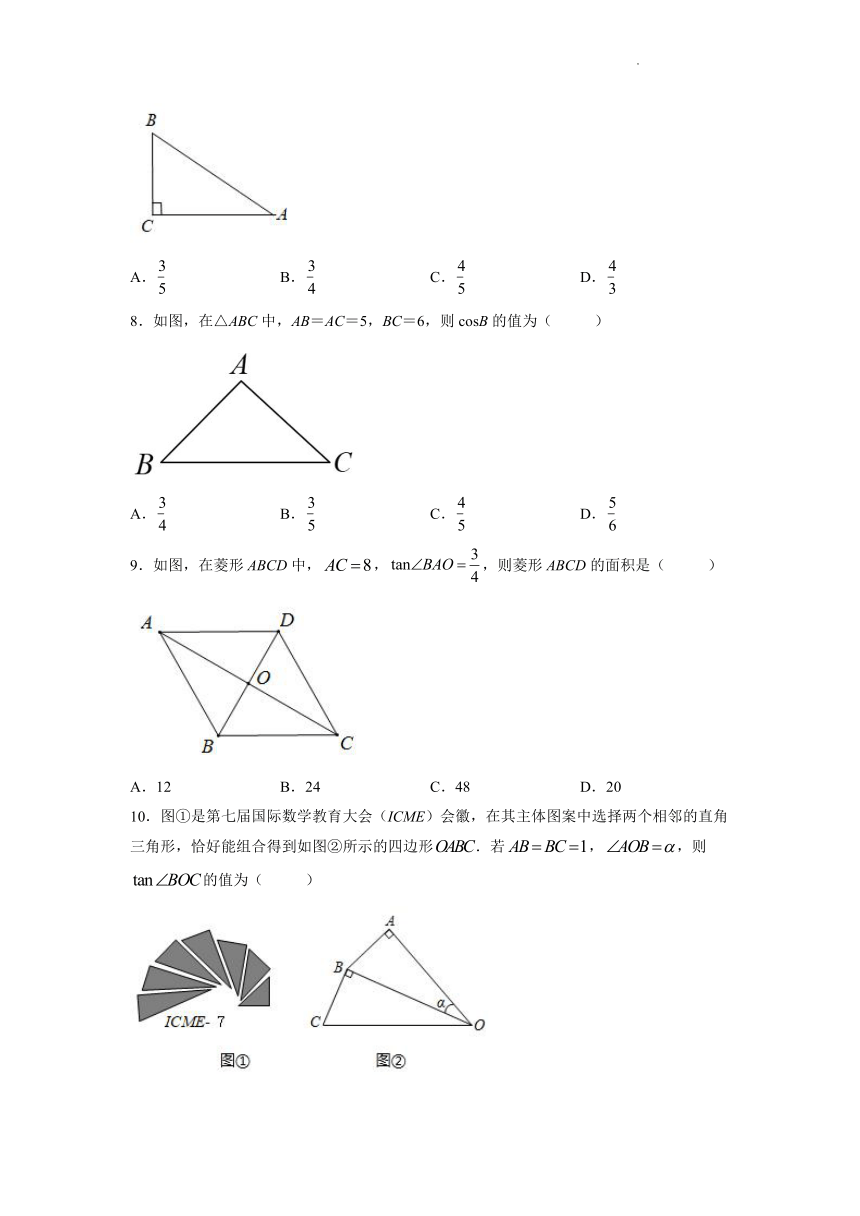
7.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,则的值为( )
A. B. C. D.
8.如图,在△ABC中,AB=AC=5,BC=6,则cosB的值为( )
A. B. C. D.
9.如图,在菱形ABCD中,,,则菱形ABCD的面积是( )
A.12 B.24 C.48 D.20
10.图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形.若,,则的值为( )
A. B. C. D.
二、填空题
11.若为锐角,且,则______°.
12.已知为锐角,且,则______度.
13.如图,在△ABC中,AC=6,BC=8,D、E分别在CA、CB上,点F在△ABC内.若四边形CDFE是边长为2的正方形,则sin∠FBA=__.
14.如图,将矩形ABCD沿CE折叠,点B恰好落在AD的F处,若AB:BC=2:3,则cos∠DCF值为=_____.
15.在Rt△ABC中,∠C=90°,若c=5,,则AC=_____.
三、解答题
16.计算:(1).
(2).
17.先化简,再求代数式的值,其中a=2cos30°﹣3tan45°.
18.如图,在中,,,.求,和.
19.如图,的直径AB垂直于弦CD,垂足为点E,连结OC、AC、BD.
(1)求证:;
(2)若,,求弧AD的长.
20.如图,在梯形ABCD中,,,,对角线AC与BD交于点E.点F是线段EC上一点,且.
(1)求证:;
(2)如果,,求FC的长.
21.如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
(1)求证:;
(2)若,S△AOD=4,求S△BOC的值.
22.如图,在ABC中,AC=12cm,AB=16cm,sinA=.
(1)求AB边上的高CD;
(2)求ABC的面积S;
(3)求tanB.
23.RtABC在直角坐标系内的位置如图所示,反比例函数y=(k≠0)在第一象限内的图象与BC边交于点D(4,1),与AB边交于点E(2,n).
求反比例函数的解析式和n值;
(2)当时,求直线AB的解析式.
【参考答案】
1.C 2.B 3.C 4.A 5.C 6.D 7.B 8.B 9.B 10.A
11.26
12.50
13.
14.
15.
16.解:(1)原式
;
(2)原式
.
17.解:原式==,
∵a=2sin60°﹣3tan45°=2×﹣3×1=﹣3,
∴原式==.
18.解:在中,,,,
∴
∴,,.
19.(1)证明:∵,
∴,
∵,
∴;
(2)解:连结OD,设的半径为r,
∵的直径AB垂直于弦CD,,
∴,,
在中,,
即,
解得,,
∵,
∴,
∴,
∴弧AD的长.
20.(1)证明:∵ ,
∴△EAD∽△ECB,
∴ ,即,
∵,∠AEB=∠DEF,
∴△ABE∽△DFE,
∴ ,
∴,
∴;
(2)解:∵, ,,
∴ ,即AC=9,
∴ ,
∵,
∴AD=3,
∵,
∴∠BAD=90°,
∴ ,
∵△EAD∽△ECB,
∴ ,
∴ , ,
∴ ,,
∴EC=6, ,
∵,
∴ ,
∴EF=4,
∴FC=EC-EF=6-4=2.
21.(1)证明: AB⊥AC,CD⊥BD,
,
,
,
,
,
又,
;
(2)解:在 中,,
,
,
,
S△AOD=4,
.
22.解:(1)如图,,,
;
(2),
;
(3)在中,,
,
.
23.(1)解:∵D(4,1)、E(2,n)在反比例函数y=的图象上,
∴4=k,2n=k,
∴k=4,n=2,
∴反比例函数的解析式为y=;
(2)解:如图1,过点E作EH⊥BC,垂足为H.
在Rt△BEH中,tan∠BEH=tan∠A=,
∵D(4,1),E(2,2),
EH=4-2=2,
∴BH=1.
∴B(4,3).
设直线AB的解析式为y=kx+b,代入B(4,3)、E(2,2),
得,解得:,
因此直线AB的函数解析式为y=x+1.
28.1锐角三角函数 课后练习
一、选择题
1.如果∠A为锐角,cosA=,那么∠A 取值范围是( )
A.0°<∠A≤30° B.30°<∠A≤45° C.45°<∠A<60° D.60°<∠A<90°
2.已知,则的度数所属范围是( )
A. B.
C. D.
3.如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的正切值( )
A.扩大为原来的两倍 B.缩小为原来的
C.不变 D.不能确定
4.已知某水库大坝的横断面为梯形,其中一斜坡AB的坡度,则斜坡AB的坡角为( )
A.30° B.45° C.60° D.150°
5.如图,在菱形ABCD中,,,,则AB的长为是( )
A.6 B.8 C.10 D.12
6.如图,小明在学校门口的点C处测得树的顶端A仰角为α,同时测得AC=15m,则树的高度AB为( )
A. B.15tanαm C. D.15sinαm
7.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,则的值为( )
A. B. C. D.
8.如图,在△ABC中,AB=AC=5,BC=6,则cosB的值为( )
A. B. C. D.
9.如图,在菱形ABCD中,,,则菱形ABCD的面积是( )
A.12 B.24 C.48 D.20
10.图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形.若,,则的值为( )
A. B. C. D.
二、填空题
11.若为锐角,且,则______°.
12.已知为锐角,且,则______度.
13.如图,在△ABC中,AC=6,BC=8,D、E分别在CA、CB上,点F在△ABC内.若四边形CDFE是边长为2的正方形,则sin∠FBA=__.
14.如图,将矩形ABCD沿CE折叠,点B恰好落在AD的F处,若AB:BC=2:3,则cos∠DCF值为=_____.
15.在Rt△ABC中,∠C=90°,若c=5,,则AC=_____.
三、解答题
16.计算:(1).
(2).
17.先化简,再求代数式的值,其中a=2cos30°﹣3tan45°.
18.如图,在中,,,.求,和.
19.如图,的直径AB垂直于弦CD,垂足为点E,连结OC、AC、BD.
(1)求证:;
(2)若,,求弧AD的长.
20.如图,在梯形ABCD中,,,,对角线AC与BD交于点E.点F是线段EC上一点,且.
(1)求证:;
(2)如果,,求FC的长.
21.如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
(1)求证:;
(2)若,S△AOD=4,求S△BOC的值.
22.如图,在ABC中,AC=12cm,AB=16cm,sinA=.
(1)求AB边上的高CD;
(2)求ABC的面积S;
(3)求tanB.
23.RtABC在直角坐标系内的位置如图所示,反比例函数y=(k≠0)在第一象限内的图象与BC边交于点D(4,1),与AB边交于点E(2,n).
求反比例函数的解析式和n值;
(2)当时,求直线AB的解析式.
【参考答案】
1.C 2.B 3.C 4.A 5.C 6.D 7.B 8.B 9.B 10.A
11.26
12.50
13.
14.
15.
16.解:(1)原式
;
(2)原式
.
17.解:原式==,
∵a=2sin60°﹣3tan45°=2×﹣3×1=﹣3,
∴原式==.
18.解:在中,,,,
∴
∴,,.
19.(1)证明:∵,
∴,
∵,
∴;
(2)解:连结OD,设的半径为r,
∵的直径AB垂直于弦CD,,
∴,,
在中,,
即,
解得,,
∵,
∴,
∴,
∴弧AD的长.
20.(1)证明:∵ ,
∴△EAD∽△ECB,
∴ ,即,
∵,∠AEB=∠DEF,
∴△ABE∽△DFE,
∴ ,
∴,
∴;
(2)解:∵, ,,
∴ ,即AC=9,
∴ ,
∵,
∴AD=3,
∵,
∴∠BAD=90°,
∴ ,
∵△EAD∽△ECB,
∴ ,
∴ , ,
∴ ,,
∴EC=6, ,
∵,
∴ ,
∴EF=4,
∴FC=EC-EF=6-4=2.
21.(1)证明: AB⊥AC,CD⊥BD,
,
,
,
,
,
又,
;
(2)解:在 中,,
,
,
,
S△AOD=4,
.
22.解:(1)如图,,,
;
(2),
;
(3)在中,,
,
.
23.(1)解:∵D(4,1)、E(2,n)在反比例函数y=的图象上,
∴4=k,2n=k,
∴k=4,n=2,
∴反比例函数的解析式为y=;
(2)解:如图1,过点E作EH⊥BC,垂足为H.
在Rt△BEH中,tan∠BEH=tan∠A=,
∵D(4,1),E(2,2),
EH=4-2=2,
∴BH=1.
∴B(4,3).
设直线AB的解析式为y=kx+b,代入B(4,3)、E(2,2),
得,解得:,
因此直线AB的函数解析式为y=x+1.
