第一章《三角形的证明》单元质量检测试卷A(含答案)
文档属性
| 名称 | 第一章《三角形的证明》单元质量检测试卷A(含答案) | 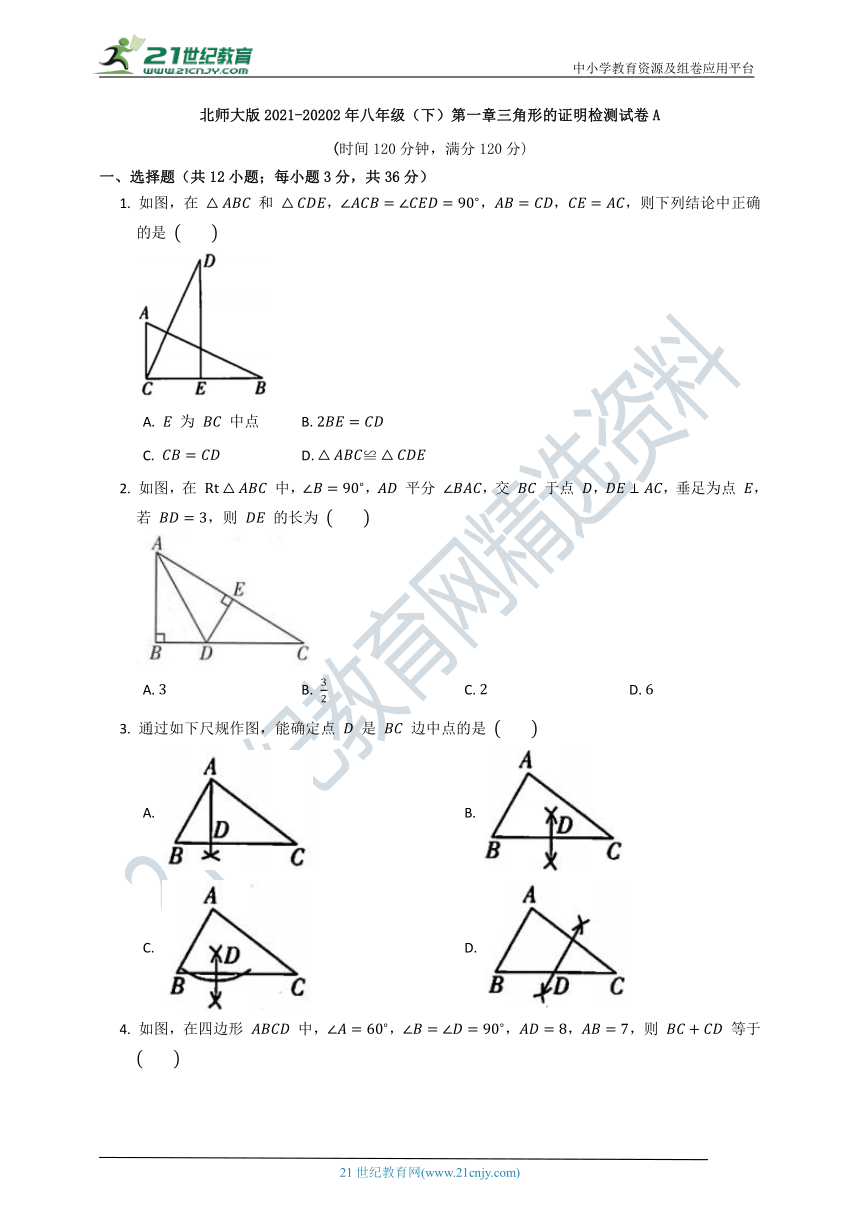 | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 07:33:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2021-20202年八年级(下)第一章三角形的证明检测试卷A
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 如图,在 和 ,,,,则下列结论中正确的是
A. 为 中点 B.
C. D.
2. 如图,在 中,, 平分 ,交 于点 ,,垂足为点 ,若 ,则 的长为
A. B. C. D.
3. 通过如下尺规作图,能确定点 是 边中点的是
A. B.
C. D.
4. 如图,在四边形 中,,,,,则 等于
A. B. C. D.
5. 下列说法中,正确的是
A. 过线段中点的直线,叫做这条线段的垂直平分线
B. 若直线 是线段 的垂直平分线,则 也是 的垂直平分线
C. 线段 的中垂线平分线段
D. 线段 的中垂线有无数条
6. 如果等腰三角形一边长为 ,另一边长为 ,那么它的周长是
A. B. C. D. 或
7. 下列说法中错误的是
A. 在 中,,则 为直角三角形
B. 在 中,若 ,则 为直角三角形
C. 在 中,若 ,,则 为直角三角形
D. 在 中,若 ,则 为直角三角形
8. 下列命题与它的逆命题都为真命题的是
A. 已知非零实数 ,如果 为分式,那么它的倒数也是分式
B. 如果 的相反数为 ,那么 为
C. 如果一个数能被 整除,那么这个数也能被 整除
D. 如果两个数的和是偶数,那么它们都是偶数
9. 在正方形网格中, 的位置如图所示,则点 ,,, 中,在 的平分线上的是
A. 点 B. 点 C. 点 D. 点
10. 下列说法中,不正确的是
A. 如果三角形 是等腰三角形,那么
B. 如果在 中,,那么 是等腰三角形
C. 如果三角形的两条边相等,那么此三角形一定是等腰三角形
D. 有两个角相等的三角形是等腰三角形
11. 老师让 个学生猜一猜这次考试中 个人的成绩谁最好.甲说:“乙最好”:乙说:“丁最好”;丙说:“反正我不是最好”;丁说:“乙说我最好,肯定错了”.老师告诉他们,只有一个人猜对了,于是,聪明的孩子们马上知道是谁的成绩最好了,你知道吗
A. 甲 B. 乙 C. 丙 D. 丁
12. 如图, 是正方形场地,点 在 的延长线上, 与 相交于点 .有甲、乙、丙三名同学同时从点 出发,甲沿着 的路径行走至 ,乙沿着 的路径行走至 ,丙沿着 的路径行走至 .若三名同学行走的速度都相同,则他们到达各自的目的地的先后顺序(由先至后)是
A. 甲乙丙 B. 丙甲乙 C. 甲丙乙 D. 乙丙甲
二、填空题(共6小题;每小题4分,共24分)
13. 如图,小马师傅用自制的工具测量零件的内孔的直径 ,已知 ,,则内孔的直径 .
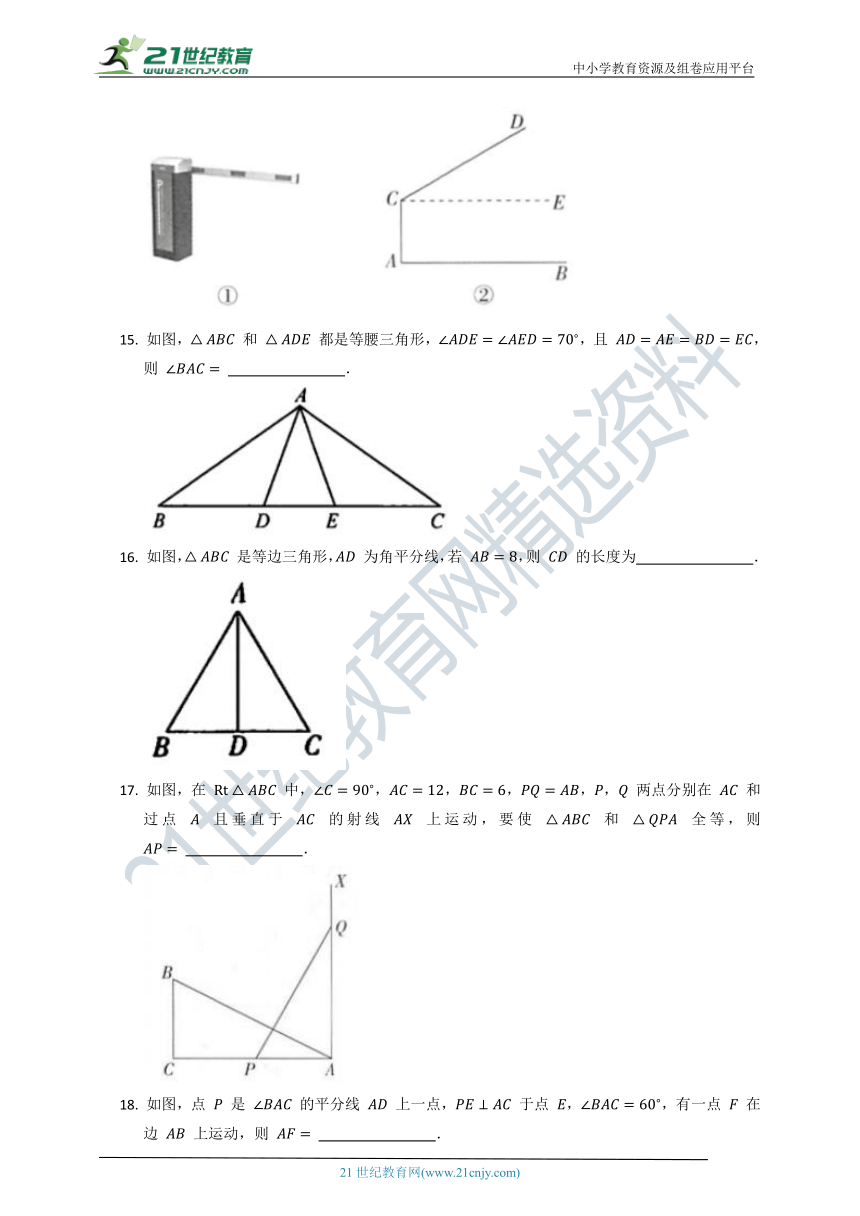
14. 图①是某小区地下车库入口的智能道闸机,图②是横杆升起时的示意图,已知 ,,,则此时点 距离地面 的高度为 .
15. 如图, 和 都是等腰三角形,,且 ,则 .
16. 如图, 是等边三角形, 为角平分线,若 ,则 的长度为 .
17. 如图,在 中,,,,,, 两点分别在 和过点 且垂直于 的射线 上运动,要使 和 全等,则 .
18. 如图,点 是 的平分线 上一点, 于点 ,,有一点 在边 上运动,则 .
三、解答题(共7小题;共60分)
19.(8分) 已知 中,,,.
(1)求证: 是直角三角形;
(2)当 时,求 , 满足的关系式.
20. (8分)如图,在等边三角形 中,,,连接 并延长,交 的延长线于点 ,求 的度数.
21. (8分)已知 的两个顶点分别为 ,,顶点 在直线 : 上.
(1)若 ,求点 的坐标.
(2) 面积为 ,设点 坐标 ,求 与 函数关系式.
(3)在直线 上是否存在点 ,使得 是直角三角形.若存在,求出点 坐标;若不存在,说明理由.
22. (8分)如图,,,,垂足为点 ,问 是等腰三角形吗 为什么
23(10分)如图,已知四边形 中,,点 是 中点,点 是 中点.
(1)求证:;
(2)过点 作 于 点,如果 平分 ,求证:.
24. (8分)如图,在四边形 中, 同时平分 和 .求证: 是 的垂直平分线.
25. (10分)如图,在 中,, 的垂直平分线分别交 , 于点 ,.
(1)若 ,,求 的周长;
(2)若 ,求 的度数.
答案
第一部分
1. D
2. A
3. B
4. B 【解析】如图,延长 , 相交于 ,
在 中,可求得 ,且 ,
计算得 ,,
于是 ,
在 中,可求得 ,且 ,
,,
于是 ,
.
5. C
6. B
7. D
8. B 【解析】A.已知非零实数 ,如果 为分式,那么它的倒数也是分式是假命题;
B.如果 的相反数为 ,那么 为 是真命题,它的逆命题是如果 为 ,那么 的相反数为 ,是真命题;
C.如果一个数能被 整除,那么这个数也能被 整除是真命题,它的逆命题是如果一个数能被 整除,那么这个数也能被 整除,是假命题;
D.如果两个数的和是偶数,那么它们都是偶数,是假命题.
故选:B.
9. B
10. A
11. C 【解析】假设甲最好,则甲说得错了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是甲最好;
假设乙最好,则甲说对了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是乙最好;
假设丙最好,则甲说错了,则乙说错了,丙说错了,丁说对了,与老师说的“只有一个人猜对了,”不矛盾,因此是丙最好;
假设丁最好,则甲说错了,则乙说对了,丙说对了,丁说错了,与老师说的“只有一个人猜对了,”矛盾,因此是丁不是最好;
因此丙的成绩最好.
12. C 【解析】 四边形 是正方形,
,,
甲行走的距离是 ;
乙行走的距离是 ;
丙行走的距离是 ,
,
,,
,,
甲比丙先到,丙比乙先到,即顺序是甲丙乙.
第二部分
13.
【解析】因为 ,
所以 ,
因为 ,
所以 是等边三角形,
所以 .
14.
【解析】如图所示,过 作 于 ,交 于点 ,
易知 ,
,,
(),
().
15.
16.
【解析】 为等边三角形,,
.
为角平分线,
,
.
17. 或
【解析】当 时,.
在 与 ,
;
当点 与点 重合时,,
在 与 中,
.
综上所述,.
18.
第三部分
19. (1) ,,,
.
是为直角三角形;
(2) ,
,
.
20. 是等边三角形,,
,.
.
,
.
.
.
21. (1)
(2) 当 时,;当 时,.
(3) 存在,,,,.
22. 是.
由 ,得 ,
由 ,得 ,
,
由 ,可得 ,
为等腰三角形.
23. (1) ,点 是 中点,
, ,
,
点 是 中点,
.
(2) 设 , 交于点 ,
,,
,
,
,
,
,
平分 ,
,
,
,
,
,
,
.
24. 同时平分 和 ,
,.
在 与 中,
().
,.
点 , 在 的垂直平分线上.
是 的垂直平分线.
25. (1) 可证 ,
所以 ,
因为 ,
所以 的周长为 .
(2) 因为 ,,
所以 ,
所以 ,
因为 ,
所以 ,
所以 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2021-20202年八年级(下)第一章三角形的证明检测试卷A
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 如图,在 和 ,,,,则下列结论中正确的是
A. 为 中点 B.
C. D.
2. 如图,在 中,, 平分 ,交 于点 ,,垂足为点 ,若 ,则 的长为
A. B. C. D.
3. 通过如下尺规作图,能确定点 是 边中点的是
A. B.
C. D.
4. 如图,在四边形 中,,,,,则 等于
A. B. C. D.
5. 下列说法中,正确的是
A. 过线段中点的直线,叫做这条线段的垂直平分线
B. 若直线 是线段 的垂直平分线,则 也是 的垂直平分线
C. 线段 的中垂线平分线段
D. 线段 的中垂线有无数条
6. 如果等腰三角形一边长为 ,另一边长为 ,那么它的周长是
A. B. C. D. 或
7. 下列说法中错误的是
A. 在 中,,则 为直角三角形
B. 在 中,若 ,则 为直角三角形
C. 在 中,若 ,,则 为直角三角形
D. 在 中,若 ,则 为直角三角形
8. 下列命题与它的逆命题都为真命题的是
A. 已知非零实数 ,如果 为分式,那么它的倒数也是分式
B. 如果 的相反数为 ,那么 为
C. 如果一个数能被 整除,那么这个数也能被 整除
D. 如果两个数的和是偶数,那么它们都是偶数
9. 在正方形网格中, 的位置如图所示,则点 ,,, 中,在 的平分线上的是
A. 点 B. 点 C. 点 D. 点
10. 下列说法中,不正确的是
A. 如果三角形 是等腰三角形,那么
B. 如果在 中,,那么 是等腰三角形
C. 如果三角形的两条边相等,那么此三角形一定是等腰三角形
D. 有两个角相等的三角形是等腰三角形
11. 老师让 个学生猜一猜这次考试中 个人的成绩谁最好.甲说:“乙最好”:乙说:“丁最好”;丙说:“反正我不是最好”;丁说:“乙说我最好,肯定错了”.老师告诉他们,只有一个人猜对了,于是,聪明的孩子们马上知道是谁的成绩最好了,你知道吗
A. 甲 B. 乙 C. 丙 D. 丁
12. 如图, 是正方形场地,点 在 的延长线上, 与 相交于点 .有甲、乙、丙三名同学同时从点 出发,甲沿着 的路径行走至 ,乙沿着 的路径行走至 ,丙沿着 的路径行走至 .若三名同学行走的速度都相同,则他们到达各自的目的地的先后顺序(由先至后)是
A. 甲乙丙 B. 丙甲乙 C. 甲丙乙 D. 乙丙甲
二、填空题(共6小题;每小题4分,共24分)
13. 如图,小马师傅用自制的工具测量零件的内孔的直径 ,已知 ,,则内孔的直径 .
14. 图①是某小区地下车库入口的智能道闸机,图②是横杆升起时的示意图,已知 ,,,则此时点 距离地面 的高度为 .
15. 如图, 和 都是等腰三角形,,且 ,则 .
16. 如图, 是等边三角形, 为角平分线,若 ,则 的长度为 .
17. 如图,在 中,,,,,, 两点分别在 和过点 且垂直于 的射线 上运动,要使 和 全等,则 .
18. 如图,点 是 的平分线 上一点, 于点 ,,有一点 在边 上运动,则 .
三、解答题(共7小题;共60分)
19.(8分) 已知 中,,,.
(1)求证: 是直角三角形;
(2)当 时,求 , 满足的关系式.
20. (8分)如图,在等边三角形 中,,,连接 并延长,交 的延长线于点 ,求 的度数.
21. (8分)已知 的两个顶点分别为 ,,顶点 在直线 : 上.
(1)若 ,求点 的坐标.
(2) 面积为 ,设点 坐标 ,求 与 函数关系式.
(3)在直线 上是否存在点 ,使得 是直角三角形.若存在,求出点 坐标;若不存在,说明理由.
22. (8分)如图,,,,垂足为点 ,问 是等腰三角形吗 为什么
23(10分)如图,已知四边形 中,,点 是 中点,点 是 中点.
(1)求证:;
(2)过点 作 于 点,如果 平分 ,求证:.
24. (8分)如图,在四边形 中, 同时平分 和 .求证: 是 的垂直平分线.
25. (10分)如图,在 中,, 的垂直平分线分别交 , 于点 ,.
(1)若 ,,求 的周长;
(2)若 ,求 的度数.
答案
第一部分
1. D
2. A
3. B
4. B 【解析】如图,延长 , 相交于 ,
在 中,可求得 ,且 ,
计算得 ,,
于是 ,
在 中,可求得 ,且 ,
,,
于是 ,
.
5. C
6. B
7. D
8. B 【解析】A.已知非零实数 ,如果 为分式,那么它的倒数也是分式是假命题;
B.如果 的相反数为 ,那么 为 是真命题,它的逆命题是如果 为 ,那么 的相反数为 ,是真命题;
C.如果一个数能被 整除,那么这个数也能被 整除是真命题,它的逆命题是如果一个数能被 整除,那么这个数也能被 整除,是假命题;
D.如果两个数的和是偶数,那么它们都是偶数,是假命题.
故选:B.
9. B
10. A
11. C 【解析】假设甲最好,则甲说得错了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是甲最好;
假设乙最好,则甲说对了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是乙最好;
假设丙最好,则甲说错了,则乙说错了,丙说错了,丁说对了,与老师说的“只有一个人猜对了,”不矛盾,因此是丙最好;
假设丁最好,则甲说错了,则乙说对了,丙说对了,丁说错了,与老师说的“只有一个人猜对了,”矛盾,因此是丁不是最好;
因此丙的成绩最好.
12. C 【解析】 四边形 是正方形,
,,
甲行走的距离是 ;
乙行走的距离是 ;
丙行走的距离是 ,
,
,,
,,
甲比丙先到,丙比乙先到,即顺序是甲丙乙.
第二部分
13.
【解析】因为 ,
所以 ,
因为 ,
所以 是等边三角形,
所以 .
14.
【解析】如图所示,过 作 于 ,交 于点 ,
易知 ,
,,
(),
().
15.
16.
【解析】 为等边三角形,,
.
为角平分线,
,
.
17. 或
【解析】当 时,.
在 与 ,
;
当点 与点 重合时,,
在 与 中,
.
综上所述,.
18.
第三部分
19. (1) ,,,
.
是为直角三角形;
(2) ,
,
.
20. 是等边三角形,,
,.
.
,
.
.
.
21. (1)
(2) 当 时,;当 时,.
(3) 存在,,,,.
22. 是.
由 ,得 ,
由 ,得 ,
,
由 ,可得 ,
为等腰三角形.
23. (1) ,点 是 中点,
, ,
,
点 是 中点,
.
(2) 设 , 交于点 ,
,,
,
,
,
,
,
平分 ,
,
,
,
,
,
,
.
24. 同时平分 和 ,
,.
在 与 中,
().
,.
点 , 在 的垂直平分线上.
是 的垂直平分线.
25. (1) 可证 ,
所以 ,
因为 ,
所以 的周长为 .
(2) 因为 ,,
所以 ,
所以 ,
因为 ,
所以 ,
所以 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
