教科版物理八年级下册 11.2 滑轮(共30张PPT)
文档属性
| 名称 | 教科版物理八年级下册 11.2 滑轮(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-08 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
滑轮
杠杆的平衡条件:
动力×动力臂 = 阻力×阻力臂
省力杠杆 —— 动力臂>阻力臂
费力杠杆 —— 动力臂<阻力臂
等臂杠杆 —— 动力臂=阻力臂
温故知新
F2
O
F1
l1
l2
l1
l2
F1
F2
O
O
F2
F1
l1
l2
O
F1
F2
l1
l2
l2
F2
l1
F1
O
省力杠杆
费力杠杆
等臂杠杆
情景引入
建筑工地上的大吊车一次就能把几吨重的混凝土或器材吊到高空作业面上,你知道吊车是怎样把它们拉上去的吗?
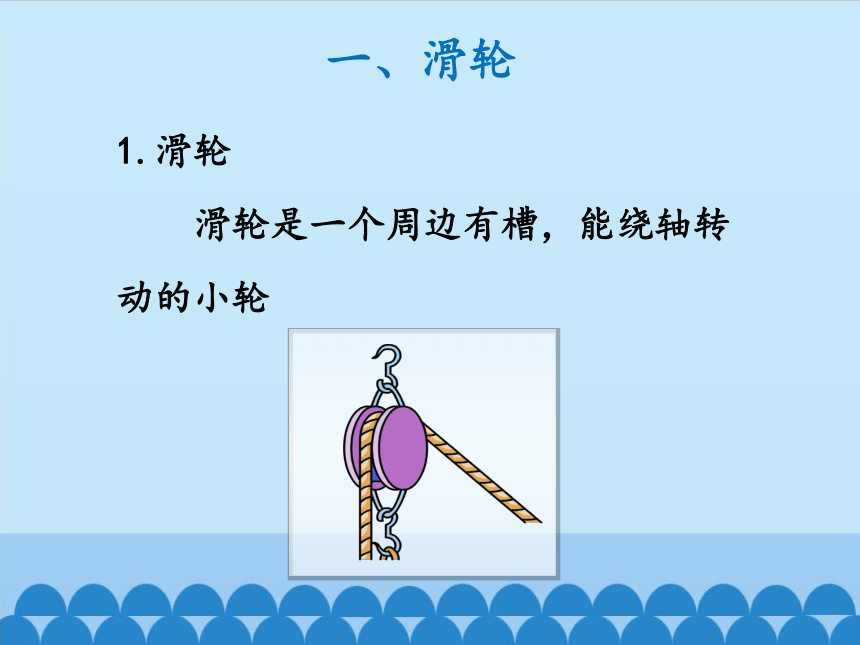
1.滑轮
滑轮是一个周边有槽,能绕轴转动的小轮
一、滑轮
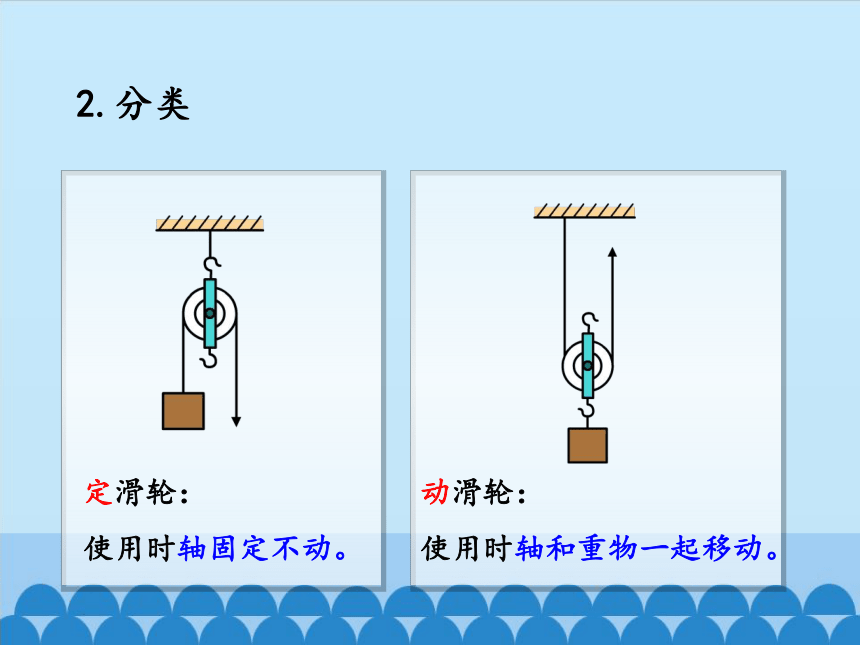
2.分类
定滑轮:
使用时轴固定不动。
动滑轮:
使用时轴和重物一起移动。
我国很早就有使用滑轮的记载,左图说明我国古代矿山早已采用滑轮做起吊机械了。
(1)能否改变用力方向?
定滑轮可以改变用力方向。
(2)能否省力?
定滑轮不能省力。
(3)能否省距离?
定滑轮不能省距离。
讨论交流:使用定滑轮
二、定滑轮
在图中,小明用力将铁块提到高处。和同学们一起讨论,你们都在哪些场合见过小明使用的这种滑轮,它能给我们带来哪些方便?
在上面的实验中,拉绳子是竖直拉的,如果斜着拉,上述实验中的结论还能成立吗?
拉力大小会变化吗?
定滑轮
想想议议
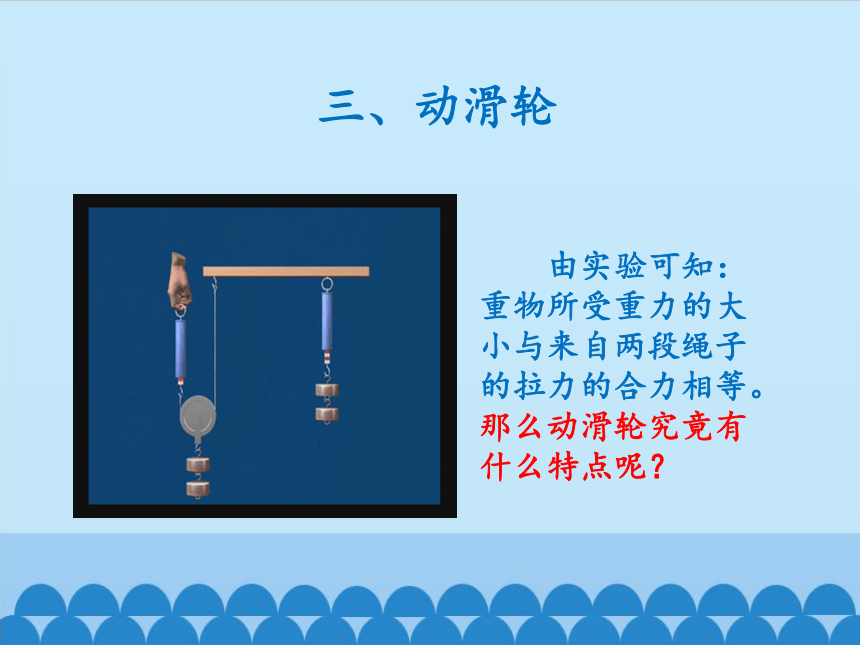
三、动滑轮
由实验可知:重物所受重力的大小与来自两段绳子的拉力的合力相等。那么动滑轮究竟有什么特点呢?
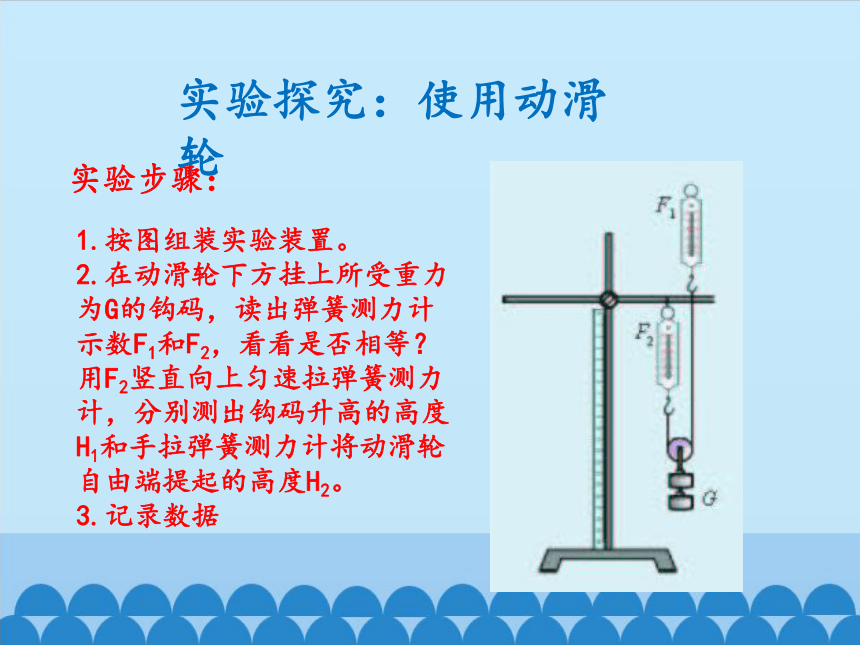
实验探究:使用动滑轮
实验步骤:
1.按图组装实验装置。
2.在动滑轮下方挂上所受重力为g的钩码,读出弹簧测力计示数f1和f2,看看是否相等?用f2竖直向上匀速拉弹簧测力计,分别测出钩码升高的高度h1和手拉弹簧测力计将动滑轮自由端提起的高度h2。
3.记录数据
数据记录
G F1 F2 H1 H2 GH1 F2H2
1
2
3
(1)不能改变用力方向。
(2)能省一半力,但费一倍距离。
F = G/2 s = 2h
(3)本质上,相当于一个动力臂为阻力臂 2 倍的省力杠杆。
小结
1. 在图中,货物 G 重为 100 牛,若不计滑轮的重力,不考虑绳子与滑轮之间的摩擦力。
由 a 图装置拉,拉
力 F1 = _____牛;
由 b 图装置拉,拉
力 F2 = _____牛。
F1
F2
a
想想做做
100
50
b
2. 物体被匀速升高时,如果 F = 25 牛,滑轮质量不计,则重物 G 受到的重力为 _____ 牛。
50
F = 25 牛
使用定滑轮能改变力的方向,但不能省力;使用动滑轮能省力,但不能改变力的方向。
那我们能不能把两者结合起来,组成滑轮组,使其既可以改变力的方向,又能省力?
思考
图中分别是两种形式滑轮的组合。和你的同学一起分析,这样的组合各有什么特点。
讨论交流:滑轮的组合
一、滑轮组
把一个定滑轮与一个动滑轮组合成滑轮组,讨论一下,你能设计出几种组合方式?把你的方案画出来。
思考
G
G
G
F
F
F
2 段绳子承担
F =(1/2)G
2 段绳子承担
F =(1/2)G
3 段绳子承担
F =(1/3)G
拉力 F 的大小与吊起动滑轮的绳子段数 n 有关。动滑轮被几段绳子吊起,所用的力就是物重的几分之一即:
F =
1
n
G
拉力 F(绳子自由端)移动距离 s 是物体上升高度 h 的 n 倍,即:
s = nh
小结
6 段绳子承担
F =(1/6)G
F
G
实例展示
F
G
7 段绳子承担
F =(1/7)G
F
18 段绳子承担
F =(1/18)G
1. 在右图所示的滑轮组中:
(a)若动滑轮重 G轮 不计,拉力 F
是多少?
F =
1
5
G物
(b)若动滑轮重 G轮 不能忽略,那么
图中的拉力 F 应等于多少?
F =
1
5
(G物+G轮)
F
G轮
G物
例题
2. 如图所示,物体 A 重为 100 N,挂重物的钩子承受的拉力是 _____ N。人匀速拉绳子的力是 _____ N(动滑轮自重不计)。
100
50
A
3. 如图所示的四个滑轮组中,图 ______ 可省一半力,图 ______ 最费力,图 ______ 和图 ______ 用力大小一样。
a
b
c
d
b
c
a
d
4. 用如图所示的滑轮组拉动物体 A,怎样绕线最省力,画出绕线图。
A
F
二、滑轮组的应用
谢 谢
滑轮
杠杆的平衡条件:
动力×动力臂 = 阻力×阻力臂
省力杠杆 —— 动力臂>阻力臂
费力杠杆 —— 动力臂<阻力臂
等臂杠杆 —— 动力臂=阻力臂
温故知新
F2
O
F1
l1
l2
l1
l2
F1
F2
O
O
F2
F1
l1
l2
O
F1
F2
l1
l2
l2
F2
l1
F1
O
省力杠杆
费力杠杆
等臂杠杆
情景引入
建筑工地上的大吊车一次就能把几吨重的混凝土或器材吊到高空作业面上,你知道吊车是怎样把它们拉上去的吗?
1.滑轮
滑轮是一个周边有槽,能绕轴转动的小轮
一、滑轮
2.分类
定滑轮:
使用时轴固定不动。
动滑轮:
使用时轴和重物一起移动。
我国很早就有使用滑轮的记载,左图说明我国古代矿山早已采用滑轮做起吊机械了。
(1)能否改变用力方向?
定滑轮可以改变用力方向。
(2)能否省力?
定滑轮不能省力。
(3)能否省距离?
定滑轮不能省距离。
讨论交流:使用定滑轮
二、定滑轮
在图中,小明用力将铁块提到高处。和同学们一起讨论,你们都在哪些场合见过小明使用的这种滑轮,它能给我们带来哪些方便?
在上面的实验中,拉绳子是竖直拉的,如果斜着拉,上述实验中的结论还能成立吗?
拉力大小会变化吗?
定滑轮
想想议议
三、动滑轮
由实验可知:重物所受重力的大小与来自两段绳子的拉力的合力相等。那么动滑轮究竟有什么特点呢?
实验探究:使用动滑轮
实验步骤:
1.按图组装实验装置。
2.在动滑轮下方挂上所受重力为g的钩码,读出弹簧测力计示数f1和f2,看看是否相等?用f2竖直向上匀速拉弹簧测力计,分别测出钩码升高的高度h1和手拉弹簧测力计将动滑轮自由端提起的高度h2。
3.记录数据
数据记录
G F1 F2 H1 H2 GH1 F2H2
1
2
3
(1)不能改变用力方向。
(2)能省一半力,但费一倍距离。
F = G/2 s = 2h
(3)本质上,相当于一个动力臂为阻力臂 2 倍的省力杠杆。
小结
1. 在图中,货物 G 重为 100 牛,若不计滑轮的重力,不考虑绳子与滑轮之间的摩擦力。
由 a 图装置拉,拉
力 F1 = _____牛;
由 b 图装置拉,拉
力 F2 = _____牛。
F1
F2
a
想想做做
100
50
b
2. 物体被匀速升高时,如果 F = 25 牛,滑轮质量不计,则重物 G 受到的重力为 _____ 牛。
50
F = 25 牛
使用定滑轮能改变力的方向,但不能省力;使用动滑轮能省力,但不能改变力的方向。
那我们能不能把两者结合起来,组成滑轮组,使其既可以改变力的方向,又能省力?
思考
图中分别是两种形式滑轮的组合。和你的同学一起分析,这样的组合各有什么特点。
讨论交流:滑轮的组合
一、滑轮组
把一个定滑轮与一个动滑轮组合成滑轮组,讨论一下,你能设计出几种组合方式?把你的方案画出来。
思考
G
G
G
F
F
F
2 段绳子承担
F =(1/2)G
2 段绳子承担
F =(1/2)G
3 段绳子承担
F =(1/3)G
拉力 F 的大小与吊起动滑轮的绳子段数 n 有关。动滑轮被几段绳子吊起,所用的力就是物重的几分之一即:
F =
1
n
G
拉力 F(绳子自由端)移动距离 s 是物体上升高度 h 的 n 倍,即:
s = nh
小结
6 段绳子承担
F =(1/6)G
F
G
实例展示
F
G
7 段绳子承担
F =(1/7)G
F
18 段绳子承担
F =(1/18)G
1. 在右图所示的滑轮组中:
(a)若动滑轮重 G轮 不计,拉力 F
是多少?
F =
1
5
G物
(b)若动滑轮重 G轮 不能忽略,那么
图中的拉力 F 应等于多少?
F =
1
5
(G物+G轮)
F
G轮
G物
例题
2. 如图所示,物体 A 重为 100 N,挂重物的钩子承受的拉力是 _____ N。人匀速拉绳子的力是 _____ N(动滑轮自重不计)。
100
50
A
3. 如图所示的四个滑轮组中,图 ______ 可省一半力,图 ______ 最费力,图 ______ 和图 ______ 用力大小一样。
a
b
c
d
b
c
a
d
4. 用如图所示的滑轮组拉动物体 A,怎样绕线最省力,画出绕线图。
A
F
二、滑轮组的应用
谢 谢
