2.2 简谐运动的描述 章节练习(Word版含答案)
文档属性
| 名称 | 2.2 简谐运动的描述 章节练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 349.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-08 23:09:24 | ||
图片预览




文档简介
2.2、简谐运动的描述
一、选择题(共16题)
1.某质点的振动图像如图所示,该质点的速度方向始终沿x轴正方向的时间段为( )
A.t=0~2s B.t=1~3s C.t=2~4s D.t=3~5s
2.如图所示,轻质弹簧下挂重力为400N的物体A,轻质弹簧伸长了4cm,再在物体A的下端用细线挂上重力为100N的物体B,弹簧均在弹性限度内。A、B两物体均静止后,将连接A、B两物体的细线剪断,则A在竖直面内做简谐运动,A运动到最高点时弹簧的形变量的大小为( )
A.1cm B.2cm C.3cm D.4cm
3.如图所示,O点为弹簧振子的平衡位置,小球在B、C间做无摩擦的往复运动。在小球运动到O的过程中,小球的( )
A.速度不断增大,加速度不断增大 B.速度不断减小,加速度不断增大
C.速度不断增大,加速度不断减小 D.速度不断减小,加速度不断减小
4.一质点做简谐运动,先后以相同的速度依次通过A、B两点,历时1s,质点通过B点后,再经过1s,第二次通过B点,在这2s内,质点的总路程是,则质点振动的周期和振幅分别可能为( )
A.2s,6cm B.4s,6cm C.4s,9cm D.2s,8cm
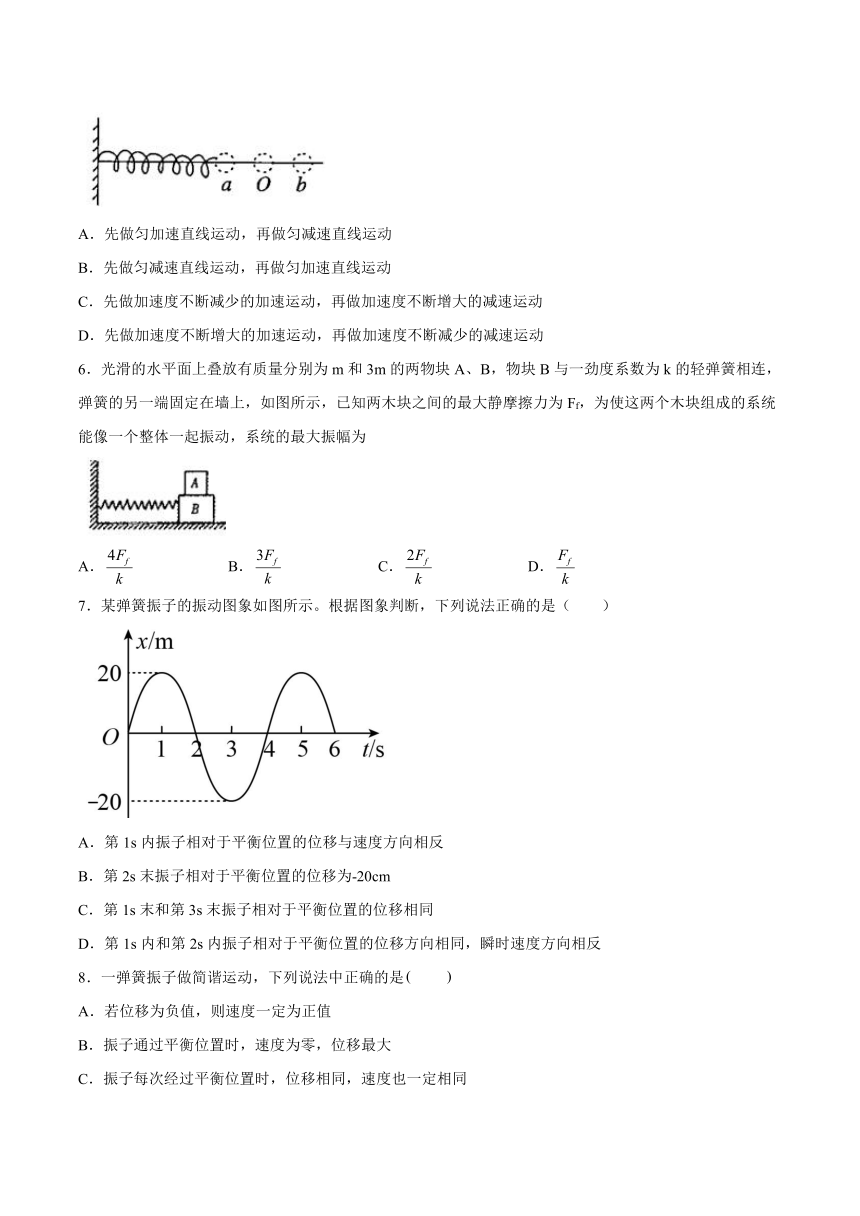
5.如图所示,弹簧振子在a、b两点间做简谐振动.当振子从a向b运动过程中,对运动描述正确的是( )
A.先做匀加速直线运动,再做匀减速直线运动
B.先做匀减速直线运动,再做匀加速直线运动
C.先做加速度不断减少的加速运动,再做加速度不断增大的减速运动
D.先做加速度不断增大的加速运动,再做加速度不断减少的减速运动
6.光滑的水平面上叠放有质量分别为m和3m的两物块A、B,物块B与一劲度系数为k的轻弹簧相连,弹簧的另一端固定在墙上,如图所示,已知两木块之间的最大静摩擦力为Ff,为使这两个木块组成的系统能像一个整体一起振动,系统的最大振幅为
A. B. C. D.
7.某弹簧振子的振动图象如图所示。根据图象判断,下列说法正确的是( )
A.第1s内振子相对于平衡位置的位移与速度方向相反
B.第2s末振子相对于平衡位置的位移为-20cm
C.第1s末和第3s末振子相对于平衡位置的位移相同
D.第1s内和第2s内振子相对于平衡位置的位移方向相同,瞬时速度方向相反
8.一弹簧振子做简谐运动,下列说法中正确的是
A.若位移为负值,则速度一定为正值
B.振子通过平衡位置时,速度为零,位移最大
C.振子每次经过平衡位置时,位移相同,速度也一定相同
D.振子每次通过同一位置时,其速度不一定相同,但位移一定相同
9.下列有关简谐运动的说法中正确的是( )
A.振子振动过程中位移不变
B.经过一个周期振子完成一次全振动
C.一分钟内完成全振动的次数,叫简谐运动的频率
D.从某位置出发,到下次经过该位置就完成一次全振动
10.某质点的振动图像如图所示,下列说法正确的是( )
A.简谐运动的表达式为y=2sin(0.5πt+0.5π) cm
B.1s到2s时间内,速度与加速度方向相同
C.t=0.5s时,位移为1cm
D.1s和3s时刻,质点的速度相同
11.如图所示,倾角为30°的斜面固定在水平地面上,其下端有一垂直于斜面的固定挡板。轻质弹簧的一端与挡板相连,另一端连接一质量为0.4kg的光滑小球(可视为质点)。现将小球由平衡位置O沿斜面向上拉动15cm至P点,使其在P、P′之间做简谐运动,M、N为斜面上关于O点对称的两点。规定沿斜面向上为正方向,已知弹簧的劲度系数为20N/m且弹簧始终处于弹性限度内,取g=10m/s2。则( )
A.小球在P点的回复力为-5N
B.小球在P′点时弹簧的形变量为25cm
C.小球从N点向上运动,经四分之三个周期,其运动的路程小于45cm
D.在M、N两点,小球的速度大小相等,弹簧的弹性势能也相等
12.一个在y方向上做简谐运动的物体,其振动图象如图所示.下列关于图(1)~(4)的判断正确的是(选项中v、F、a分别表示物体的速度、受到的回复力和加速度)
A.图(1)可作为该物体的v-t图象
B.图(2)可作为该物体的F-t图象
C.图(3)可作为该物体的F-t图象
D.图(4)可作为该物体的a-t图象
13.如图所示为某弹簧振子在0~5s内的振动图象,由图可知,下列说法中正确的是( )
A.振动周期为5s,振幅为8cm
B.第2s末振子的速度为零,加速度为负向的最大值
C.从第1s末到第2s末振子在做加速运动
D.第3s末振子的速度为正向的最大值
14.一弹簧振子做简谐运动,其位移x与时间t的关系曲线如图所示,由图可知( )
A.质点的振幅为10cm
B.质点的振动频率是0.25Hz
C.t=2s时刻质点的速度最大,方向沿x轴正方向
D.t=3s时刻质点的加速度最大,方向沿x轴正方向
15.如图所示两木块A和B叠放在光滑水平面上,质量分别为m和M,A与 B之间的最大静摩擦力为Ffm,B与劲度系数为k的轻质弹簧连接构成弹簧振子,已知A和B在振动过程中不发生相对滑动,则
A.速度最大时,A、B间摩擦力最大
B.弹簧弹力最大时,A、B间摩擦力最大
C.它们的振幅不能大于
D.它们的振幅不能大于
16.做简谐运动的弹簧振子,质量为m,最大速率为v,则下列说法正确的是( )
A.从某一时刻算起,在半个周期的时间内,回复力做的功一定为零
B.从某一时刻算起,在半个周期的时间内,回复力做的功可能是0到mv2之间的某一个值
C.从某一时刻算起,在半个周期的时间内,速度变化量一定为零
D.从某一时刻算起,在半个周期的时间内,速度变化量的大小可能是0到2v之间的某一个值
二、填空题
17.如图所示是某一质点作简谐运动的振动图像,则该质点的振动周期为_______s,在t=3s时速度为______(选填“正方向最大”、“负方向最大”、“零”)。
18.某实验小组利用数字实验系统探究弹簧振子的运动规律,装置如图所示,水平光滑导轨上的滑块与轻弹簧组成弹簧振子,滑块上固定有传感器的发射器,把弹簧拉长5cm后由静止释放,滑块开始振动,他们分析位移—时间图象后发现,滑块的运动是简谐运动,滑块从最右端运动到最左端所用时间为1s,则弹簧振子的振动频率为______Hz;以释放的瞬时为初始时刻、向右为正方向,则滑块运动的表达式为x=______cm。
19.质点的振动图象如图所示,由图象可知,振幅为________米,振动周期为________秒,振动频率为________赫兹。
20.如图所示是用频闪照相的方法拍到的一个弹簧振子的振动情况,甲图是振子静止在平衡位置的照片,乙图是振子被拉伸到左侧距平衡位置20cm处,放手后向右运动周期的频闪照片,已知频闪的频率为10Hz,则振子的振动周期为T=________s,而在t=T/12时刻振子的位置坐标________15cm.(选填“大于”、“小于”或“等于”).
三、综合题
21.两个简谐运动的表达式分别为和,求它们的振幅之比、各自的频率以及它们的相位差。
22.一弹簧振子沿x轴做简谐运动,在内以相同的速度先后经过A、B两点,又经过,再次经过B点,已知弹簧振子的振幅A=5cm,求:
(1)弹簧振子的振动周期;
(2)3s内振子通过的路程。
23.如图所示,两木块1、2的质量分别为m、M,竖直轻弹簧劲度系数为k,下端与木块2连接,木块1与弹簧不连接.现将木块1下压一段距离后释放,木块1沿竖直方向做简谐运动,振动过程中,木块1始终没有离开弹簧.求:
(1)木块1振动的振幅的最大值;
(2)木块1以最大振幅振动时,木块2对地面的最大压力.
24.一个弹簧振子做简谐运动,频率为,振幅为.当振子具有最大正向速度的瞬时开始计时,在图画出振动图像.
( )
试卷第1页,共3页
参考答案:
1.C
【详解】
A.0~2s内质点的速度方向始终沿x轴负方向,故A不符合题意;
B.1~3s内质点的速度方向先沿x轴负方向,后沿x轴正方向,故B不符合题意;
C.2~4s内质点的速度方向始终沿x轴正方向,故C符合题意;
D.3~5s内质点的速度方向先沿x轴正方向,后沿x轴负方向,故D不符合题意。
故选C。
2.C
【详解】
弹簧的劲度系数为
再在物体A的下端用细线挂上重力为100N的物体B,则此时弹簧再伸长
将连接A、B两物体的细线剪断,则A在竖直面内做简谐运动,平衡位置在弹簧伸长4cm的位置,由对称性可知,A运动到最高点时弹簧的形变量的大小为
x=4cm-1cm=3cm
故选C。
3.C
【详解】
无论是小球从左边还是从右边运动到O的过程中,弹簧的弹力对小球都是做正功,小球的速度变大,回复力减小,则根据F=ma可知,加速度减小。故C正确,ABD错误。
故选C。
4.B
【详解】
简谐运动的质点,先后以同样大小的速度通过A、B两点,
则可判定这两点关于平衡位置O点对称,
所以质点由A到O时间与由O到B的时间相等。
那么平衡位置O到B点的时间
因过B点后再经过质点以方向相反、大小相同的速度再次通过B点,
则有从B点到最大位置的时间
因此,质点振动的周期是
质点总路程的一半,即为振幅。
所以振幅为
故B正确,ACD错误。
故选B。
5.C
【详解】
AB.由于弹簧振子的加速度是由弹簧形变提供的,根据牛顿第二定律可知,弹簧弹力时刻在变,因此加速度也在变,不可能为匀变速运动,故AB错误;
CD.从a到o运动的过程中,合力向右,是加速运动,根据公式
加速度不断减小,故从a到o是加速度不断减小的加速运动;从o到b的过程,速度向右,加速度向左,根据公式可知,加速度不断增大,故从o到b做加速度不断增加的减速运动,故C正确D错误.
6.A
【详解】
两个物块组成的系统一起做简谐运动时,两者之间存在相对运动趋势,产生静摩擦力,物块B对A的静摩擦力提供A的回复力.当两物块之间的静摩擦力达到最大时,系统的振幅达到最大,设为A.根据牛顿第二定律,对A有:Ff=mam,对整体有:kA=(m+3m)am,联立可得:A=,故A正确,BCD错误。
7.D
【详解】
A.第1s内振子相对于平衡位置的位移与速度均为正值,则方向相同,选项A错误;
B.第2s末振子回到平衡位置,则相对于平衡位置的位移为0,选项B错误;
C.第1s末和第3s末振子相对于平衡位置的位移大小相同,但是方向相反,选项C错误;
D.第1s内和第2s内振子相对于平衡位置的位移方向相同,瞬时速度方向相反,选项D正确。
故选D。
8.D
【详解】
若位移为负值,由,可知加速度一定为正值,而速度有两种可能的方向,所以速度不一定为正值,A错误;质点通过平衡位置时,速度最大,加速度为零,B错误;质点每次通过平衡位置时,位移相同,加速度一定相同,而速度有两种可能的方向,不一定相同,C错误;质点每次通过同一位置时,位移相同,加速度一定相同,因为速度有两种可能的方向,所以速度不一定相同,D正确.
9.B
【详解】
A.在弹簧振子的振动过程中,振子的位移随时间不断变化,A错误;
B.弹簧振子完成一次全振动的时间是一个周期,B正确;
C.每秒钟内完成全振动的次数叫简谐运动的频率,C错误;
D.从某位置出发,到下次经过该位置并且速度相同才能称为一次全振动,故从某位置出发,到下次经过该位置不一定是完成一次全振动,D错误。
故选B。
10.A
【详解】
A.振幅为2cm,周期为4s,则角速度为
故简谐振动的表达式为
在图中选取一点带入表达式中求出
故故简谐振动的表达式为
故A正确;
B.1s到2s时间内,质点做减速运动,故速度与加速度反向,故B错误;
C.将t=0.5s带入表达式可得
故位移小于,故C错误;
D.y-t图像中斜率表示速度,1s和3s时刻速度大小相等,方向相反,故D错误。
故选A。
11.B
【详解】
A.O点为平衡位置,沿斜面向上拉动15cm后,小球受到的合力为
则小球在P点的回复力为-3N,故A错误;
B.由简谐运动的对称性可知,小球在P′点的回复力为3N,有
解得
故B正确;
C.小球经平衡位置O时,速度最大,前四分之一周期内运动的路程要大于15cm,后二分之一周期内运动的路程为30cm,总路程大于45cm,故C错误;
D.根据简谐运动的对称性可知,小球在M、N两点速度大小相等。由系统机械能守恒可知,小球在N点时弹簧的弹性势能大于小球在M点时弹簧的弹性势能,故D错误。
故选B。
12.C
【详解】
据题意,从该振动图像可知,当物体从0时刻开始向正方向运动,位移x增加,据回复力公式:可知回复力反向增加,据牛顿第二定律可知加速度也与位移反向增加,由于回复力与速度方向相反则速度减小,故选项C正确而选项A、B、D错误.
13.D
【详解】
A.振幅是位移的最大值的大小,故振幅8cm,而周期是完成一次全振动的时间,振动周期为4s,A错误;
B.第2s末振子的速度为零,加速度为正向的最大值,B错误;
C.从第1s末到第2s末振子在做减速运动,C错误;
D.第3s末振子的位移为零,振子经过平衡位置,故速度最大,且方向为正,D正确。
故选D。
14.BC
【详解】
A.由图可知质点的振幅
故A错误;
B.由图可知
则振动频率
故B正确;
C.t=2s时质点的位移为零,位于平衡位置,质点的速度最大,方向沿x轴正方向,故C正确;
D.t=3s时质点的位移为正向最大,由
可知质点的加速度为负向最大,故D错误。
故选BC。
15.BD
【详解】
A.因为 A和B在振动过程中不发生相对滑动,所以加速度相同;当速度最大时,,对A分析,受力为0,故A、B间摩擦力为0,A错误
B.对A、B整体受力分析,,隔离A分析:,所以弹力最大时,加速度最大,A、B间摩擦力最大,B正确
C.、D.通过选项C的分析,设最大振幅为A,当振幅最大时,弹力最大:整体分析,隔离A分析:联立两式得:,C错误D正确
16.AD
【详解】
AB、做简谐运动的弹簧振子,经过半个周期的时间,振子的速度大小一定相等,初动能与末动能一定相等,根据动能定理得知,回复力做的功一定为零,故A正确,B错误;
CD、若从最大位移处算起,在半个周期的时间内,速度变化量最小,大小为零;若从平衡位置算起,在半个周期的时间内,速度变化量最大,大小为2v,则速度变化量大小可能是零到2v之间的某一个值,故C错误,D正确;
故选AD.
17. 4 正方向最大
【详解】
根据振动图象可得振动周期T=4s;在t=3s时质点在平衡位置,此时速度最大,根据振动图象可知速度方向向正方向。
18. 0.5 5cosπt
【详解】
滑块从最右端运动到最左端所用时间为ls,知周期T=2s,则振动频率
f==0.5Hz
由
ω=2πf=π
根据
x=Asin(ωt+φ)
可知
A=5cm
φ=
所以
x=5sin(πt+)=5cosπt(cm)
19. 0.3 0.02 50
【详解】
由质点的振动图象可知,振幅为
振动的周期为
振动频率为
20. 1.2 大于
【详解】
由图乙可看出,振子在四分之一周期的时间为,所以T=1.2s;由图乙可知在t=T/12时刻振子的位置坐标大于15cm.
21.,,π
【详解】
由简谐运动的表达式
x=Asin(ωx+φ)
可知
A1=4a
A2=2a
所以
A1∶A2=2∶1,
ω1=ω2=4πb
根据
ω=2πf
可得
f1=f2=2b
它们的相位差是
Δφ=(4πbt+π)-(4πbt+π)=π
22.(1)1.2s;(2)50cm。
【详解】
(1)由题意可知AB关于平衡位置O对称,C为最大位移处,运动情况如图
则有,解得T=1.2s
(2)3s内振子振动2.5个周期,则振子通过的路程s=2.5×4A=50cm;
【详解】
(1)在平衡位置,弹簧的压缩量x0=
要使木块1振动过程中不离开弹簧,木块1在最高点处时由重力充当回复力,弹簧恰好恢复原长,故木块1振动的振幅最大值为x0=
(2)木块1以最大振幅振动时,木块1到最低点时,弹簧的压缩量最大,为2x0,此时弹簧对木块2的压力最大,木块2对地面的压力最大;木块2对地面的压力N=Mg+k·2x0=Mg+2mg
24.
【详解】
质点做简谐运动,运动的周期为
当振子具有最大正向速度的瞬时开始计时,其振动图像是余弦曲线,则振动图像如下图所示
答案第1页,共2页
一、选择题(共16题)
1.某质点的振动图像如图所示,该质点的速度方向始终沿x轴正方向的时间段为( )
A.t=0~2s B.t=1~3s C.t=2~4s D.t=3~5s
2.如图所示,轻质弹簧下挂重力为400N的物体A,轻质弹簧伸长了4cm,再在物体A的下端用细线挂上重力为100N的物体B,弹簧均在弹性限度内。A、B两物体均静止后,将连接A、B两物体的细线剪断,则A在竖直面内做简谐运动,A运动到最高点时弹簧的形变量的大小为( )
A.1cm B.2cm C.3cm D.4cm
3.如图所示,O点为弹簧振子的平衡位置,小球在B、C间做无摩擦的往复运动。在小球运动到O的过程中,小球的( )
A.速度不断增大,加速度不断增大 B.速度不断减小,加速度不断增大
C.速度不断增大,加速度不断减小 D.速度不断减小,加速度不断减小
4.一质点做简谐运动,先后以相同的速度依次通过A、B两点,历时1s,质点通过B点后,再经过1s,第二次通过B点,在这2s内,质点的总路程是,则质点振动的周期和振幅分别可能为( )
A.2s,6cm B.4s,6cm C.4s,9cm D.2s,8cm
5.如图所示,弹簧振子在a、b两点间做简谐振动.当振子从a向b运动过程中,对运动描述正确的是( )
A.先做匀加速直线运动,再做匀减速直线运动
B.先做匀减速直线运动,再做匀加速直线运动
C.先做加速度不断减少的加速运动,再做加速度不断增大的减速运动
D.先做加速度不断增大的加速运动,再做加速度不断减少的减速运动
6.光滑的水平面上叠放有质量分别为m和3m的两物块A、B,物块B与一劲度系数为k的轻弹簧相连,弹簧的另一端固定在墙上,如图所示,已知两木块之间的最大静摩擦力为Ff,为使这两个木块组成的系统能像一个整体一起振动,系统的最大振幅为
A. B. C. D.
7.某弹簧振子的振动图象如图所示。根据图象判断,下列说法正确的是( )
A.第1s内振子相对于平衡位置的位移与速度方向相反
B.第2s末振子相对于平衡位置的位移为-20cm
C.第1s末和第3s末振子相对于平衡位置的位移相同
D.第1s内和第2s内振子相对于平衡位置的位移方向相同,瞬时速度方向相反
8.一弹簧振子做简谐运动,下列说法中正确的是
A.若位移为负值,则速度一定为正值
B.振子通过平衡位置时,速度为零,位移最大
C.振子每次经过平衡位置时,位移相同,速度也一定相同
D.振子每次通过同一位置时,其速度不一定相同,但位移一定相同
9.下列有关简谐运动的说法中正确的是( )
A.振子振动过程中位移不变
B.经过一个周期振子完成一次全振动
C.一分钟内完成全振动的次数,叫简谐运动的频率
D.从某位置出发,到下次经过该位置就完成一次全振动
10.某质点的振动图像如图所示,下列说法正确的是( )
A.简谐运动的表达式为y=2sin(0.5πt+0.5π) cm
B.1s到2s时间内,速度与加速度方向相同
C.t=0.5s时,位移为1cm
D.1s和3s时刻,质点的速度相同
11.如图所示,倾角为30°的斜面固定在水平地面上,其下端有一垂直于斜面的固定挡板。轻质弹簧的一端与挡板相连,另一端连接一质量为0.4kg的光滑小球(可视为质点)。现将小球由平衡位置O沿斜面向上拉动15cm至P点,使其在P、P′之间做简谐运动,M、N为斜面上关于O点对称的两点。规定沿斜面向上为正方向,已知弹簧的劲度系数为20N/m且弹簧始终处于弹性限度内,取g=10m/s2。则( )
A.小球在P点的回复力为-5N
B.小球在P′点时弹簧的形变量为25cm
C.小球从N点向上运动,经四分之三个周期,其运动的路程小于45cm
D.在M、N两点,小球的速度大小相等,弹簧的弹性势能也相等
12.一个在y方向上做简谐运动的物体,其振动图象如图所示.下列关于图(1)~(4)的判断正确的是(选项中v、F、a分别表示物体的速度、受到的回复力和加速度)
A.图(1)可作为该物体的v-t图象
B.图(2)可作为该物体的F-t图象
C.图(3)可作为该物体的F-t图象
D.图(4)可作为该物体的a-t图象
13.如图所示为某弹簧振子在0~5s内的振动图象,由图可知,下列说法中正确的是( )
A.振动周期为5s,振幅为8cm
B.第2s末振子的速度为零,加速度为负向的最大值
C.从第1s末到第2s末振子在做加速运动
D.第3s末振子的速度为正向的最大值
14.一弹簧振子做简谐运动,其位移x与时间t的关系曲线如图所示,由图可知( )
A.质点的振幅为10cm
B.质点的振动频率是0.25Hz
C.t=2s时刻质点的速度最大,方向沿x轴正方向
D.t=3s时刻质点的加速度最大,方向沿x轴正方向
15.如图所示两木块A和B叠放在光滑水平面上,质量分别为m和M,A与 B之间的最大静摩擦力为Ffm,B与劲度系数为k的轻质弹簧连接构成弹簧振子,已知A和B在振动过程中不发生相对滑动,则
A.速度最大时,A、B间摩擦力最大
B.弹簧弹力最大时,A、B间摩擦力最大
C.它们的振幅不能大于
D.它们的振幅不能大于
16.做简谐运动的弹簧振子,质量为m,最大速率为v,则下列说法正确的是( )
A.从某一时刻算起,在半个周期的时间内,回复力做的功一定为零
B.从某一时刻算起,在半个周期的时间内,回复力做的功可能是0到mv2之间的某一个值
C.从某一时刻算起,在半个周期的时间内,速度变化量一定为零
D.从某一时刻算起,在半个周期的时间内,速度变化量的大小可能是0到2v之间的某一个值
二、填空题
17.如图所示是某一质点作简谐运动的振动图像,则该质点的振动周期为_______s,在t=3s时速度为______(选填“正方向最大”、“负方向最大”、“零”)。
18.某实验小组利用数字实验系统探究弹簧振子的运动规律,装置如图所示,水平光滑导轨上的滑块与轻弹簧组成弹簧振子,滑块上固定有传感器的发射器,把弹簧拉长5cm后由静止释放,滑块开始振动,他们分析位移—时间图象后发现,滑块的运动是简谐运动,滑块从最右端运动到最左端所用时间为1s,则弹簧振子的振动频率为______Hz;以释放的瞬时为初始时刻、向右为正方向,则滑块运动的表达式为x=______cm。
19.质点的振动图象如图所示,由图象可知,振幅为________米,振动周期为________秒,振动频率为________赫兹。
20.如图所示是用频闪照相的方法拍到的一个弹簧振子的振动情况,甲图是振子静止在平衡位置的照片,乙图是振子被拉伸到左侧距平衡位置20cm处,放手后向右运动周期的频闪照片,已知频闪的频率为10Hz,则振子的振动周期为T=________s,而在t=T/12时刻振子的位置坐标________15cm.(选填“大于”、“小于”或“等于”).
三、综合题
21.两个简谐运动的表达式分别为和,求它们的振幅之比、各自的频率以及它们的相位差。
22.一弹簧振子沿x轴做简谐运动,在内以相同的速度先后经过A、B两点,又经过,再次经过B点,已知弹簧振子的振幅A=5cm,求:
(1)弹簧振子的振动周期;
(2)3s内振子通过的路程。
23.如图所示,两木块1、2的质量分别为m、M,竖直轻弹簧劲度系数为k,下端与木块2连接,木块1与弹簧不连接.现将木块1下压一段距离后释放,木块1沿竖直方向做简谐运动,振动过程中,木块1始终没有离开弹簧.求:
(1)木块1振动的振幅的最大值;
(2)木块1以最大振幅振动时,木块2对地面的最大压力.
24.一个弹簧振子做简谐运动,频率为,振幅为.当振子具有最大正向速度的瞬时开始计时,在图画出振动图像.
( )
试卷第1页,共3页
参考答案:
1.C
【详解】
A.0~2s内质点的速度方向始终沿x轴负方向,故A不符合题意;
B.1~3s内质点的速度方向先沿x轴负方向,后沿x轴正方向,故B不符合题意;
C.2~4s内质点的速度方向始终沿x轴正方向,故C符合题意;
D.3~5s内质点的速度方向先沿x轴正方向,后沿x轴负方向,故D不符合题意。
故选C。
2.C
【详解】
弹簧的劲度系数为
再在物体A的下端用细线挂上重力为100N的物体B,则此时弹簧再伸长
将连接A、B两物体的细线剪断,则A在竖直面内做简谐运动,平衡位置在弹簧伸长4cm的位置,由对称性可知,A运动到最高点时弹簧的形变量的大小为
x=4cm-1cm=3cm
故选C。
3.C
【详解】
无论是小球从左边还是从右边运动到O的过程中,弹簧的弹力对小球都是做正功,小球的速度变大,回复力减小,则根据F=ma可知,加速度减小。故C正确,ABD错误。
故选C。
4.B
【详解】
简谐运动的质点,先后以同样大小的速度通过A、B两点,
则可判定这两点关于平衡位置O点对称,
所以质点由A到O时间与由O到B的时间相等。
那么平衡位置O到B点的时间
因过B点后再经过质点以方向相反、大小相同的速度再次通过B点,
则有从B点到最大位置的时间
因此,质点振动的周期是
质点总路程的一半,即为振幅。
所以振幅为
故B正确,ACD错误。
故选B。
5.C
【详解】
AB.由于弹簧振子的加速度是由弹簧形变提供的,根据牛顿第二定律可知,弹簧弹力时刻在变,因此加速度也在变,不可能为匀变速运动,故AB错误;
CD.从a到o运动的过程中,合力向右,是加速运动,根据公式
加速度不断减小,故从a到o是加速度不断减小的加速运动;从o到b的过程,速度向右,加速度向左,根据公式可知,加速度不断增大,故从o到b做加速度不断增加的减速运动,故C正确D错误.
6.A
【详解】
两个物块组成的系统一起做简谐运动时,两者之间存在相对运动趋势,产生静摩擦力,物块B对A的静摩擦力提供A的回复力.当两物块之间的静摩擦力达到最大时,系统的振幅达到最大,设为A.根据牛顿第二定律,对A有:Ff=mam,对整体有:kA=(m+3m)am,联立可得:A=,故A正确,BCD错误。
7.D
【详解】
A.第1s内振子相对于平衡位置的位移与速度均为正值,则方向相同,选项A错误;
B.第2s末振子回到平衡位置,则相对于平衡位置的位移为0,选项B错误;
C.第1s末和第3s末振子相对于平衡位置的位移大小相同,但是方向相反,选项C错误;
D.第1s内和第2s内振子相对于平衡位置的位移方向相同,瞬时速度方向相反,选项D正确。
故选D。
8.D
【详解】
若位移为负值,由,可知加速度一定为正值,而速度有两种可能的方向,所以速度不一定为正值,A错误;质点通过平衡位置时,速度最大,加速度为零,B错误;质点每次通过平衡位置时,位移相同,加速度一定相同,而速度有两种可能的方向,不一定相同,C错误;质点每次通过同一位置时,位移相同,加速度一定相同,因为速度有两种可能的方向,所以速度不一定相同,D正确.
9.B
【详解】
A.在弹簧振子的振动过程中,振子的位移随时间不断变化,A错误;
B.弹簧振子完成一次全振动的时间是一个周期,B正确;
C.每秒钟内完成全振动的次数叫简谐运动的频率,C错误;
D.从某位置出发,到下次经过该位置并且速度相同才能称为一次全振动,故从某位置出发,到下次经过该位置不一定是完成一次全振动,D错误。
故选B。
10.A
【详解】
A.振幅为2cm,周期为4s,则角速度为
故简谐振动的表达式为
在图中选取一点带入表达式中求出
故故简谐振动的表达式为
故A正确;
B.1s到2s时间内,质点做减速运动,故速度与加速度反向,故B错误;
C.将t=0.5s带入表达式可得
故位移小于,故C错误;
D.y-t图像中斜率表示速度,1s和3s时刻速度大小相等,方向相反,故D错误。
故选A。
11.B
【详解】
A.O点为平衡位置,沿斜面向上拉动15cm后,小球受到的合力为
则小球在P点的回复力为-3N,故A错误;
B.由简谐运动的对称性可知,小球在P′点的回复力为3N,有
解得
故B正确;
C.小球经平衡位置O时,速度最大,前四分之一周期内运动的路程要大于15cm,后二分之一周期内运动的路程为30cm,总路程大于45cm,故C错误;
D.根据简谐运动的对称性可知,小球在M、N两点速度大小相等。由系统机械能守恒可知,小球在N点时弹簧的弹性势能大于小球在M点时弹簧的弹性势能,故D错误。
故选B。
12.C
【详解】
据题意,从该振动图像可知,当物体从0时刻开始向正方向运动,位移x增加,据回复力公式:可知回复力反向增加,据牛顿第二定律可知加速度也与位移反向增加,由于回复力与速度方向相反则速度减小,故选项C正确而选项A、B、D错误.
13.D
【详解】
A.振幅是位移的最大值的大小,故振幅8cm,而周期是完成一次全振动的时间,振动周期为4s,A错误;
B.第2s末振子的速度为零,加速度为正向的最大值,B错误;
C.从第1s末到第2s末振子在做减速运动,C错误;
D.第3s末振子的位移为零,振子经过平衡位置,故速度最大,且方向为正,D正确。
故选D。
14.BC
【详解】
A.由图可知质点的振幅
故A错误;
B.由图可知
则振动频率
故B正确;
C.t=2s时质点的位移为零,位于平衡位置,质点的速度最大,方向沿x轴正方向,故C正确;
D.t=3s时质点的位移为正向最大,由
可知质点的加速度为负向最大,故D错误。
故选BC。
15.BD
【详解】
A.因为 A和B在振动过程中不发生相对滑动,所以加速度相同;当速度最大时,,对A分析,受力为0,故A、B间摩擦力为0,A错误
B.对A、B整体受力分析,,隔离A分析:,所以弹力最大时,加速度最大,A、B间摩擦力最大,B正确
C.、D.通过选项C的分析,设最大振幅为A,当振幅最大时,弹力最大:整体分析,隔离A分析:联立两式得:,C错误D正确
16.AD
【详解】
AB、做简谐运动的弹簧振子,经过半个周期的时间,振子的速度大小一定相等,初动能与末动能一定相等,根据动能定理得知,回复力做的功一定为零,故A正确,B错误;
CD、若从最大位移处算起,在半个周期的时间内,速度变化量最小,大小为零;若从平衡位置算起,在半个周期的时间内,速度变化量最大,大小为2v,则速度变化量大小可能是零到2v之间的某一个值,故C错误,D正确;
故选AD.
17. 4 正方向最大
【详解】
根据振动图象可得振动周期T=4s;在t=3s时质点在平衡位置,此时速度最大,根据振动图象可知速度方向向正方向。
18. 0.5 5cosπt
【详解】
滑块从最右端运动到最左端所用时间为ls,知周期T=2s,则振动频率
f==0.5Hz
由
ω=2πf=π
根据
x=Asin(ωt+φ)
可知
A=5cm
φ=
所以
x=5sin(πt+)=5cosπt(cm)
19. 0.3 0.02 50
【详解】
由质点的振动图象可知,振幅为
振动的周期为
振动频率为
20. 1.2 大于
【详解】
由图乙可看出,振子在四分之一周期的时间为,所以T=1.2s;由图乙可知在t=T/12时刻振子的位置坐标大于15cm.
21.,,π
【详解】
由简谐运动的表达式
x=Asin(ωx+φ)
可知
A1=4a
A2=2a
所以
A1∶A2=2∶1,
ω1=ω2=4πb
根据
ω=2πf
可得
f1=f2=2b
它们的相位差是
Δφ=(4πbt+π)-(4πbt+π)=π
22.(1)1.2s;(2)50cm。
【详解】
(1)由题意可知AB关于平衡位置O对称,C为最大位移处,运动情况如图
则有,解得T=1.2s
(2)3s内振子振动2.5个周期,则振子通过的路程s=2.5×4A=50cm;
【详解】
(1)在平衡位置,弹簧的压缩量x0=
要使木块1振动过程中不离开弹簧,木块1在最高点处时由重力充当回复力,弹簧恰好恢复原长,故木块1振动的振幅最大值为x0=
(2)木块1以最大振幅振动时,木块1到最低点时,弹簧的压缩量最大,为2x0,此时弹簧对木块2的压力最大,木块2对地面的压力最大;木块2对地面的压力N=Mg+k·2x0=Mg+2mg
24.
【详解】
质点做简谐运动,运动的周期为
当振子具有最大正向速度的瞬时开始计时,其振动图像是余弦曲线,则振动图像如下图所示
答案第1页,共2页
