初中物理 人教版 八年级下册12.1杠杆课件(共22张PPT)
文档属性
| 名称 | 初中物理 人教版 八年级下册12.1杠杆课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-08 22:29:41 | ||
图片预览






文档简介
(共22张PPT)
简单机械之杠杆
杠杆
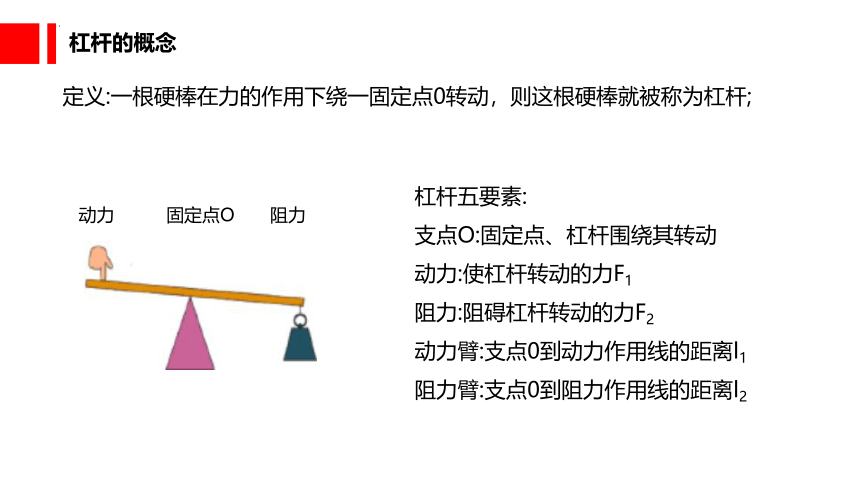
杠杆的概念
杠杆五要素:
支点O:固定点、杠杆围绕其转动
动力:使杠杆转动的力F1
阻力:阻碍杠杆转动的力F2
动力臂:支点0到动力作用线的距离l1
阻力臂:支点0到阻力作用线的距离l2
定义:一根硬棒在力的作用下绕一固定点0转动,则这根硬棒就被称为杠杆;
动力
阻力
固定点O
杠杆的概念
①硬棒,不一定是直的 ②绕固定点旋转
定义:一根硬棒在力的作用下绕一固定点0转动,则这根硬棒就被称为杠杆;
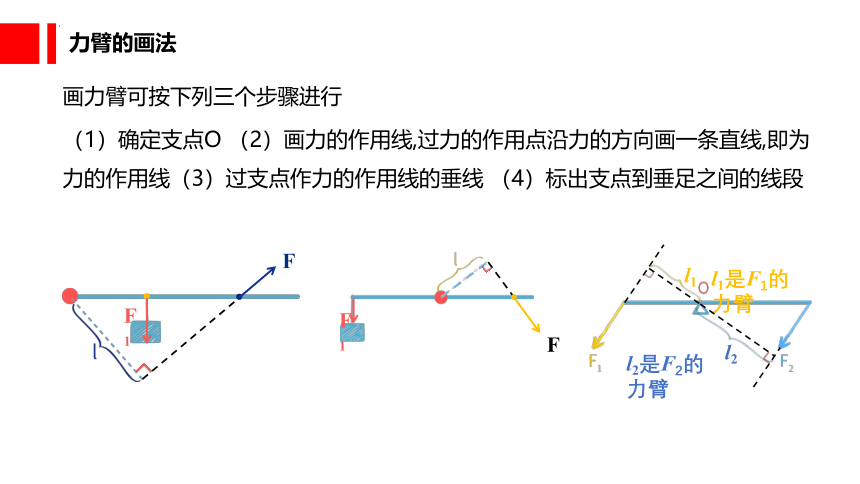
力臂的画法
(1)确定支点O (2)画力的作用线,过力的作用点沿力的方向画一条直线,即为力的作用线(3)过支点作力的作用线的垂线 (4)标出支点到垂足之间的线段
画力臂可按下列三个步骤进行
l1是F1的力臂
l2是F2的力臂
l1
l2
F1
F
F1
F
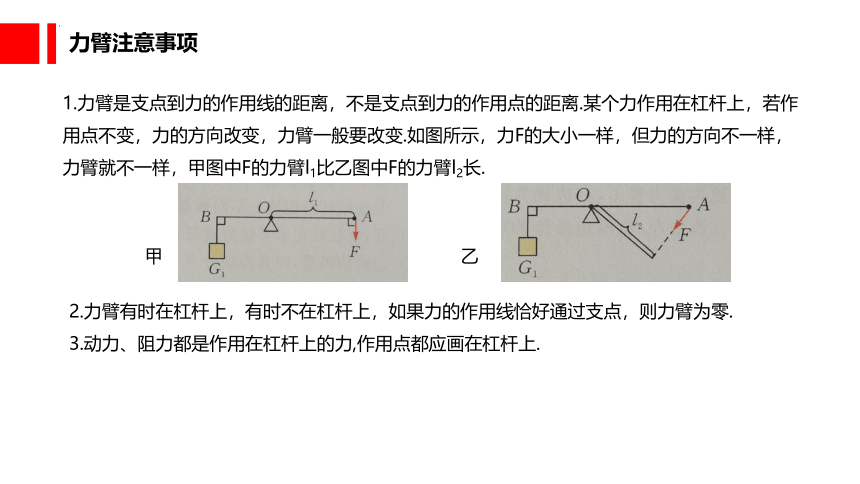
力臂注意事项
1.力臂是支点到力的作用线的距离,不是支点到力的作用点的距离.某个力作用在杠杆上,若作用点不变,力的方向改变,力臂一般要改变.如图所示,力F的大小一样,但力的方向不一样,力臂就不一样,甲图中F的力臂l1比乙图中F的力臂l2长.
2.力臂有时在杠杆上,有时不在杠杆上,如果力的作用线恰好通过支点,则力臂为零.
3.动力、阻力都是作用在杠杆上的力,作用点都应画在杠杆上.
甲
乙
杠杆的分类
杠杆的分类:根据杠杆模型可知,若L1〉L2,则F1〈F2,这是杠杆可省力;若L1〈L2,则F1〉F2,这时杠杆要费力;若L1=L2,则F1=F2,杠杆既不省力也不费力,根据动力臂与阻力臂的不同,我们可以把杠杆分为三类:省力杠杆、费力杠杆和等臂杠杆;
一类:支点在动力点和阻力点的之间。称为第一类杠杆。既可能省力的,也可能费力的,主要由支点的位置决定,或者说由臂的长度决定。动力臂与阻力臂长度一致,所以这类杠杆是等臂杠杆。例:跷跷板、天平等;
杠杆的分类
二类:阻力点在动力点和支点中间。称为第二类杠杆。由于动力臂总是大于阻力臂,所以它是省力杠杆。例:坚果夹子,门,钉书机,跳水板,扳手,开(啤酒)瓶器,(运水泥、砖的)手推车;
三类:动力点在支点和阻力点之间。称为第三类杠杆。特点是动力臂比阻力臂短,所以这类杠杆是费力杠杆,然而能够节省距离。例:镊子,手臂,鱼竿,皮划艇的桨,下颚,锹、扫帚、球棍,理发剪刀等以一手为支点,一手为动力的器械。
杠杆的平衡条件
杠杆平衡是指杠杆处于静止状态或者匀速转动状态,杠杆平衡不仅仅指杠杆静止或杠杆水平静止。
杠杆的平衡条件为:动力x动力臂=阻力x阻力臂 数学表达式为:F1 l1=F2 l2
杠杆转动方向的判断
(1)当F1l1≠F2l2时,杠杆的平衡即被破坏,原来静止的杠杆就要转动起来,原来匀速转动的杠杆将变速转动;
(2)影响杠杆转动的因素:杠杆是否转动、怎样转动,应看F1L1与F2l2的大小关系,并不单纯取决于F1、F2的大小关系,也不单纯取决于力臂l1和l2的大小关系.,也就是说,影响杠杆转动的因素不单是力,也不单是力臂,而是力和力臂的乘积.
(3)转动方向的判断:当F1l1>F2l2时,杠杆沿F1的方向转动:当F1l1杠杆平衡的判断:
力×力臂-力×力臂
若F1l1 - F2l2>0 向 F1 偏转
若F1l1 - F2l2 = 0 平衡
若F1l1 - F2l2<0 向 F2 偏转
杠杆最省力问题
1.使杠杆最省力的方法
使杠杆平衡时,若要让所用的动力最小,由F1l1=F2l2,可知有下列两种方法:(1)阻力F2和阻力臂l2一定时,增大动力臂,则动力F1会减小,动力臂越长,则所需的动力就越小,以支点到力的作用点间的距离作力臂是最长的力臂,所用的动力最小。如1图,将油桶推上台阶,油桶与台阶接触的点是它转动的支点O,要使所用的推力最小,要在油桶上找一距O点最远的点A,以OA为力臂,则力的方向与 OA垂直且向上。
(2)阻力F2和动力臂l1一定时,减小阻力臂l2,动力也会减小,阻力臂越短,则动力就越小,如图乙所示,卸货车要将车厢内的货物卸下,此时货物的重力可以认为是车厢转动的阻力F2,它是一定的,车厢受顶的推力的力臂即动力的力臂l1也是一定的,货物装在在靠车尾的一端,比装在车厢前端的阻力臂要小一些,所以顶的推力会小些。
F
G
O
图1
图2
杠杆最省力问题
作杠杆最省力的力臂
由杠杆平衡条件F1L1=F2L2,对于支点、阻力和阻力臂已定的杠杆F2L2是一定的,F1与L1成反比,所以要使杠杆使用时的动力F1最小,那么就要F1的力臂L1最长;
作最省力的力臂的方法是在杠杆上找到一个点使这个点离支点最远,以这个点到支点的距离作为力臂,相对应的作用于这一点并以此为力臂的力就是最小的力。
练习
1.下列属于费力杠杆的是( )
A.天平
B.钓鱼竿
C.铡刀
D.瓶盖起子
【解答】解:A、天平在使用过程中,动力臂等于阻力臂,属于等臂杠杆,故A不符合题意;B、钓鱼竿在使用过程中,动力臂小于阻力臂,属于费力杠杆,故B符合题意;C、铡刀在使用过程中,动力臂大于阻力臂,属于省力杠杆,故C不符合题意;D、开瓶起子在使用过程中,动力臂大于阻力臂,属于省力杠杆,故D不符合题意。故选:B。
练习
2.如图,当人手握铅球向上运动时,肌肉产生的力使前臂骨骼绕肘关节转动。下列所示的杠杆中,与人的前臂属于同种杠杆的是( )
A.(1)(2) B.(2)(3) C.(3)(4) D.(2)(4)
【解答】解:当人手握铅球向上运动时,肌肉产生的力使前臂骨骼绕肘关节转动,此时动力臂小于阻力臂,是费力杠杆(1)钓鱼竿在使用过程中,动力臂大于阻力臂,是费力杠杆,故(1)符合题意;(2)筷子在使用过程中,动力臂小于阻力臂,是费力杠杆,故(2)符合题意;(3)核桃夹在使用过程中,动力臂大于阻力臂,是省力杠杆,故(3)不合题意;(4)天平在使用过程中,动力臂等于阻力臂,是等臂杠杆,故(4)不合题意。故选:A。
练习
3.如图所示,轻质杠杆OA可绕O点转动,OB=AB,用细线将重物悬挂在A点,在B点作用竖直向上的拉力F。则在保持杠杆水平静止的情况下( )
A.拉力F的大小为物重的0.5倍 B.当重物的悬挂点右移时,F将增大 C.若F改为沿图中虚线方向施力,F将减小 D.若物重减小2N,F的大小将减小4N
【解答】解:A、由图可知,OB=AB,阻力的力臂为动力力臂的2倍,根据杠杆的平衡条件F×OB=G×OA可知,拉力F的大小为物重的2倍,故A错误;B、当悬挂点右移时,动力臂、阻力不变,阻力臂变小,则动力F将变小,故B错误;C、保持杠杆在水平位置平衡,将拉力F转至虚线位置时,拉力的力臂变小,因为阻力与阻力臂不变,由杠杆的平衡条件可知,拉力变大,故C错误;D、若物重减小2N,根据杠杆的平衡条件可知,F的减小量为2N×2=4N,故D正确。故选:D。
练习
4.如图所示的两种情况中,OB=AB,物重均为G,两轻质杠杆均处于水平平衡状态,比较力F、F′的大小,满足关系式( )
A.F=F′ B.F=2F′ C.4F=F′ D.2F=F′
【解答】解:(1)左图中,LOB是阻力臂,LOA是动力臂,因为LOB=LAB,所以LOB= LOA,又因为FLOA=GLOB,所以F= G﹣﹣﹣﹣﹣﹣①
(2)右图中,LOB是动力臂,LOA是阻力臂,因为F′LOB=GLOA,所以F′=2G﹣﹣﹣﹣﹣②,由①②可知:4F=F′。故选:C。
练习
5.士兵用力缓慢匀速拉动绳子,把吊桥AB(杠杆)吊起,下列说法正确的是( )
A.当杠杆AB处于水平时是费力杠杆 B.当杠杆AB缓慢匀速升至虚线位置的过程,动力减小 C.当杠杆AB缓慢匀速升至虚线位置的过程,阻力臂增大 D.当杠杆AB缓慢匀速升至虚线位置的过程,动力臂先减小后增大
【解答】解:由图可知,支点为A,绳子对吊桥AB的拉力(动力)方向沿BC方向;从A作BC的垂线,该垂线段为动力臂L,如图所示:吊桥的重力为阻力,则阻力臂L2=OA;已知∠ABC=45°,则ΔBDA为等腰直角三角形,根据几何知识可知动力臂L1= AB,而阻力臂L2=OA= AB,所以此时的动力臂大于阻力臂,为省力杠杆;在缓慢匀速拉升至虚线位置的过程,动力臂变大,阻力臂变小,而阻力大小不变,根据F1L1=F2L2可知,动力减小;故ACD错误,B正确。故选:B。
练习
6.如图A所示的杠杆是平衡的,在此杠杆支点两侧的物体下方分别加挂一个同样物体,如图B所示,那么,以下说法中正确的是( )
A.杠杆仍然平衡 B.杠杆可能平衡 C.杠杆一定不能平衡 D.杠杆是否平衡与加挂物体的质量有关
【解答】解:由图A知,杠杆此时处于平衡状态,设每个钩码的重力为G,每节杠杆的长度为L,即有:2G×2L=G×4L;当物体下方分别加挂一个相同的小球G球时,则:左边=(G球+2G)×2L=G球×2L+2G×2L,右边=(G球+G)×L=G球×4L+G×4L,可得右边增大的力和力臂的乘积较大,所以杠杆不平衡,将向B端倾斜,且与加挂物体的质量无关,故ABD错误,C正确。故选:C。
练习
7.如图所示,一重物悬挂在轻质杠杆的中点处,在杠杆的最右端施加一个始终竖直向上的F,使杠杆在水平位置保持平衡,下列说法正确的是( )
A.若将重物向左移动,保持杠杆水平平衡,则F将变大B.将杠杆沿顺时针方向缓慢转动,F将不变 C.将杠杆沿逆时针方向缓慢转动,F将变大 D.若将重物和F的作用点向左移动相等的距离,且保持F大小不变,杠杆仍能在原位置平衡
练习
【解答】解:(1)由题知,杠杆最右端的力F竖直向上(方向不变),当重物向左移动时,重物对杠杆拉力的力臂L2变小,F的力臂L1不变(等于杠杆的长),阻力G不变,由杠杆平衡条件FL1=GL2可知,力F将变小,故A错误;(2)将杠杆沿顺时针方向缓慢转动,如图所示重物悬挂在杠杆的中点,水平平衡时,动力臂和阻力臂的关系为:L1=2L2,保持力F方向不变,杠杆顺时针方向缓慢转动后,由上面右图结合相似三角形知识可知,动力臂和阻力臂的关系:L1′=2L2′,物重G不变,动力臂与阻力臂的比值不变,由杠杆平衡条件可知,动力F的大小始终等于 G,即力F将不变,故B正确;(3)将杠杆沿逆时针方向缓慢转动,道理同(2),力F将不变,故C错误;(4)开始时杠杆平衡,即FL1=GL2,因为L1>L2,所以F<G;若将重物和F的作用点向左移动相等的距离,即F(L1﹣L)=FL1﹣FL,G(L2﹣L)=GL2﹣GL,因为F<G,所FL1﹣FL>GL2﹣GL,杠杆不会在原位置平衡,故D错误。故选:B。
练习
8. 如图所示,不考虑杠杆重力,作出阻力F2和使杠杆平衡的最小动力F1。
练习
9. 如图所示是某校物理实验小组探究杠杆平衡条件的实验装置。(1)若发现杠杆在使用前右端低左端高,要使它在水平位置平衡,可将杠杆左端的平衡螺母向____调节。此后在整个实验过程中,是否还要再旋动两侧的平衡螺母?__________(选填“是”或“否”)。(2)一实验小组得到的两组数据如下表所示:
实验序号 动力F1/N 动力臂l1/cm 阻力F2/N 阻力臂l2/cm
1 2 20 1 10
2 1 8 2 4
这两组数据中,实验序号为_____的一组肯定有错误。经检查,发现是测量动力臂时读错了,动力臂的实际值比记录值大还是小?_______。(3)通过此探究实验应该得出的结论是:____________________________。(4)另一实验小组的同学获得的数据如下表所示:
练习
动力F1/N 动力臂l1/cm 阻力F2/N 阻力臂l2/cm
4 5 5 4
他们得出的结论是:“动力+动力臂=阻力+阻力臂”。你认为他们的实验存在什么问题?_________________________________________________
解答:(1)左;否(2)1;小(3)动力×动力臂=阻力×阻力臂(4)根据一次实验,得出的实验结论不具有普遍性,不同单位的物理量之间不能相加
简单机械之杠杆
杠杆
杠杆的概念
杠杆五要素:
支点O:固定点、杠杆围绕其转动
动力:使杠杆转动的力F1
阻力:阻碍杠杆转动的力F2
动力臂:支点0到动力作用线的距离l1
阻力臂:支点0到阻力作用线的距离l2
定义:一根硬棒在力的作用下绕一固定点0转动,则这根硬棒就被称为杠杆;
动力
阻力
固定点O
杠杆的概念
①硬棒,不一定是直的 ②绕固定点旋转
定义:一根硬棒在力的作用下绕一固定点0转动,则这根硬棒就被称为杠杆;
力臂的画法
(1)确定支点O (2)画力的作用线,过力的作用点沿力的方向画一条直线,即为力的作用线(3)过支点作力的作用线的垂线 (4)标出支点到垂足之间的线段
画力臂可按下列三个步骤进行
l1是F1的力臂
l2是F2的力臂
l1
l2
F1
F
F1
F
力臂注意事项
1.力臂是支点到力的作用线的距离,不是支点到力的作用点的距离.某个力作用在杠杆上,若作用点不变,力的方向改变,力臂一般要改变.如图所示,力F的大小一样,但力的方向不一样,力臂就不一样,甲图中F的力臂l1比乙图中F的力臂l2长.
2.力臂有时在杠杆上,有时不在杠杆上,如果力的作用线恰好通过支点,则力臂为零.
3.动力、阻力都是作用在杠杆上的力,作用点都应画在杠杆上.
甲
乙
杠杆的分类
杠杆的分类:根据杠杆模型可知,若L1〉L2,则F1〈F2,这是杠杆可省力;若L1〈L2,则F1〉F2,这时杠杆要费力;若L1=L2,则F1=F2,杠杆既不省力也不费力,根据动力臂与阻力臂的不同,我们可以把杠杆分为三类:省力杠杆、费力杠杆和等臂杠杆;
一类:支点在动力点和阻力点的之间。称为第一类杠杆。既可能省力的,也可能费力的,主要由支点的位置决定,或者说由臂的长度决定。动力臂与阻力臂长度一致,所以这类杠杆是等臂杠杆。例:跷跷板、天平等;
杠杆的分类
二类:阻力点在动力点和支点中间。称为第二类杠杆。由于动力臂总是大于阻力臂,所以它是省力杠杆。例:坚果夹子,门,钉书机,跳水板,扳手,开(啤酒)瓶器,(运水泥、砖的)手推车;
三类:动力点在支点和阻力点之间。称为第三类杠杆。特点是动力臂比阻力臂短,所以这类杠杆是费力杠杆,然而能够节省距离。例:镊子,手臂,鱼竿,皮划艇的桨,下颚,锹、扫帚、球棍,理发剪刀等以一手为支点,一手为动力的器械。
杠杆的平衡条件
杠杆平衡是指杠杆处于静止状态或者匀速转动状态,杠杆平衡不仅仅指杠杆静止或杠杆水平静止。
杠杆的平衡条件为:动力x动力臂=阻力x阻力臂 数学表达式为:F1 l1=F2 l2
杠杆转动方向的判断
(1)当F1l1≠F2l2时,杠杆的平衡即被破坏,原来静止的杠杆就要转动起来,原来匀速转动的杠杆将变速转动;
(2)影响杠杆转动的因素:杠杆是否转动、怎样转动,应看F1L1与F2l2的大小关系,并不单纯取决于F1、F2的大小关系,也不单纯取决于力臂l1和l2的大小关系.,也就是说,影响杠杆转动的因素不单是力,也不单是力臂,而是力和力臂的乘积.
(3)转动方向的判断:当F1l1>F2l2时,杠杆沿F1的方向转动:当F1l1
力×力臂-力×力臂
若F1l1 - F2l2>0 向 F1 偏转
若F1l1 - F2l2 = 0 平衡
若F1l1 - F2l2<0 向 F2 偏转
杠杆最省力问题
1.使杠杆最省力的方法
使杠杆平衡时,若要让所用的动力最小,由F1l1=F2l2,可知有下列两种方法:(1)阻力F2和阻力臂l2一定时,增大动力臂,则动力F1会减小,动力臂越长,则所需的动力就越小,以支点到力的作用点间的距离作力臂是最长的力臂,所用的动力最小。如1图,将油桶推上台阶,油桶与台阶接触的点是它转动的支点O,要使所用的推力最小,要在油桶上找一距O点最远的点A,以OA为力臂,则力的方向与 OA垂直且向上。
(2)阻力F2和动力臂l1一定时,减小阻力臂l2,动力也会减小,阻力臂越短,则动力就越小,如图乙所示,卸货车要将车厢内的货物卸下,此时货物的重力可以认为是车厢转动的阻力F2,它是一定的,车厢受顶的推力的力臂即动力的力臂l1也是一定的,货物装在在靠车尾的一端,比装在车厢前端的阻力臂要小一些,所以顶的推力会小些。
F
G
O
图1
图2
杠杆最省力问题
作杠杆最省力的力臂
由杠杆平衡条件F1L1=F2L2,对于支点、阻力和阻力臂已定的杠杆F2L2是一定的,F1与L1成反比,所以要使杠杆使用时的动力F1最小,那么就要F1的力臂L1最长;
作最省力的力臂的方法是在杠杆上找到一个点使这个点离支点最远,以这个点到支点的距离作为力臂,相对应的作用于这一点并以此为力臂的力就是最小的力。
练习
1.下列属于费力杠杆的是( )
A.天平
B.钓鱼竿
C.铡刀
D.瓶盖起子
【解答】解:A、天平在使用过程中,动力臂等于阻力臂,属于等臂杠杆,故A不符合题意;B、钓鱼竿在使用过程中,动力臂小于阻力臂,属于费力杠杆,故B符合题意;C、铡刀在使用过程中,动力臂大于阻力臂,属于省力杠杆,故C不符合题意;D、开瓶起子在使用过程中,动力臂大于阻力臂,属于省力杠杆,故D不符合题意。故选:B。
练习
2.如图,当人手握铅球向上运动时,肌肉产生的力使前臂骨骼绕肘关节转动。下列所示的杠杆中,与人的前臂属于同种杠杆的是( )
A.(1)(2) B.(2)(3) C.(3)(4) D.(2)(4)
【解答】解:当人手握铅球向上运动时,肌肉产生的力使前臂骨骼绕肘关节转动,此时动力臂小于阻力臂,是费力杠杆(1)钓鱼竿在使用过程中,动力臂大于阻力臂,是费力杠杆,故(1)符合题意;(2)筷子在使用过程中,动力臂小于阻力臂,是费力杠杆,故(2)符合题意;(3)核桃夹在使用过程中,动力臂大于阻力臂,是省力杠杆,故(3)不合题意;(4)天平在使用过程中,动力臂等于阻力臂,是等臂杠杆,故(4)不合题意。故选:A。
练习
3.如图所示,轻质杠杆OA可绕O点转动,OB=AB,用细线将重物悬挂在A点,在B点作用竖直向上的拉力F。则在保持杠杆水平静止的情况下( )
A.拉力F的大小为物重的0.5倍 B.当重物的悬挂点右移时,F将增大 C.若F改为沿图中虚线方向施力,F将减小 D.若物重减小2N,F的大小将减小4N
【解答】解:A、由图可知,OB=AB,阻力的力臂为动力力臂的2倍,根据杠杆的平衡条件F×OB=G×OA可知,拉力F的大小为物重的2倍,故A错误;B、当悬挂点右移时,动力臂、阻力不变,阻力臂变小,则动力F将变小,故B错误;C、保持杠杆在水平位置平衡,将拉力F转至虚线位置时,拉力的力臂变小,因为阻力与阻力臂不变,由杠杆的平衡条件可知,拉力变大,故C错误;D、若物重减小2N,根据杠杆的平衡条件可知,F的减小量为2N×2=4N,故D正确。故选:D。
练习
4.如图所示的两种情况中,OB=AB,物重均为G,两轻质杠杆均处于水平平衡状态,比较力F、F′的大小,满足关系式( )
A.F=F′ B.F=2F′ C.4F=F′ D.2F=F′
【解答】解:(1)左图中,LOB是阻力臂,LOA是动力臂,因为LOB=LAB,所以LOB= LOA,又因为FLOA=GLOB,所以F= G﹣﹣﹣﹣﹣﹣①
(2)右图中,LOB是动力臂,LOA是阻力臂,因为F′LOB=GLOA,所以F′=2G﹣﹣﹣﹣﹣②,由①②可知:4F=F′。故选:C。
练习
5.士兵用力缓慢匀速拉动绳子,把吊桥AB(杠杆)吊起,下列说法正确的是( )
A.当杠杆AB处于水平时是费力杠杆 B.当杠杆AB缓慢匀速升至虚线位置的过程,动力减小 C.当杠杆AB缓慢匀速升至虚线位置的过程,阻力臂增大 D.当杠杆AB缓慢匀速升至虚线位置的过程,动力臂先减小后增大
【解答】解:由图可知,支点为A,绳子对吊桥AB的拉力(动力)方向沿BC方向;从A作BC的垂线,该垂线段为动力臂L,如图所示:吊桥的重力为阻力,则阻力臂L2=OA;已知∠ABC=45°,则ΔBDA为等腰直角三角形,根据几何知识可知动力臂L1= AB,而阻力臂L2=OA= AB,所以此时的动力臂大于阻力臂,为省力杠杆;在缓慢匀速拉升至虚线位置的过程,动力臂变大,阻力臂变小,而阻力大小不变,根据F1L1=F2L2可知,动力减小;故ACD错误,B正确。故选:B。
练习
6.如图A所示的杠杆是平衡的,在此杠杆支点两侧的物体下方分别加挂一个同样物体,如图B所示,那么,以下说法中正确的是( )
A.杠杆仍然平衡 B.杠杆可能平衡 C.杠杆一定不能平衡 D.杠杆是否平衡与加挂物体的质量有关
【解答】解:由图A知,杠杆此时处于平衡状态,设每个钩码的重力为G,每节杠杆的长度为L,即有:2G×2L=G×4L;当物体下方分别加挂一个相同的小球G球时,则:左边=(G球+2G)×2L=G球×2L+2G×2L,右边=(G球+G)×L=G球×4L+G×4L,可得右边增大的力和力臂的乘积较大,所以杠杆不平衡,将向B端倾斜,且与加挂物体的质量无关,故ABD错误,C正确。故选:C。
练习
7.如图所示,一重物悬挂在轻质杠杆的中点处,在杠杆的最右端施加一个始终竖直向上的F,使杠杆在水平位置保持平衡,下列说法正确的是( )
A.若将重物向左移动,保持杠杆水平平衡,则F将变大B.将杠杆沿顺时针方向缓慢转动,F将不变 C.将杠杆沿逆时针方向缓慢转动,F将变大 D.若将重物和F的作用点向左移动相等的距离,且保持F大小不变,杠杆仍能在原位置平衡
练习
【解答】解:(1)由题知,杠杆最右端的力F竖直向上(方向不变),当重物向左移动时,重物对杠杆拉力的力臂L2变小,F的力臂L1不变(等于杠杆的长),阻力G不变,由杠杆平衡条件FL1=GL2可知,力F将变小,故A错误;(2)将杠杆沿顺时针方向缓慢转动,如图所示重物悬挂在杠杆的中点,水平平衡时,动力臂和阻力臂的关系为:L1=2L2,保持力F方向不变,杠杆顺时针方向缓慢转动后,由上面右图结合相似三角形知识可知,动力臂和阻力臂的关系:L1′=2L2′,物重G不变,动力臂与阻力臂的比值不变,由杠杆平衡条件可知,动力F的大小始终等于 G,即力F将不变,故B正确;(3)将杠杆沿逆时针方向缓慢转动,道理同(2),力F将不变,故C错误;(4)开始时杠杆平衡,即FL1=GL2,因为L1>L2,所以F<G;若将重物和F的作用点向左移动相等的距离,即F(L1﹣L)=FL1﹣FL,G(L2﹣L)=GL2﹣GL,因为F<G,所FL1﹣FL>GL2﹣GL,杠杆不会在原位置平衡,故D错误。故选:B。
练习
8. 如图所示,不考虑杠杆重力,作出阻力F2和使杠杆平衡的最小动力F1。
练习
9. 如图所示是某校物理实验小组探究杠杆平衡条件的实验装置。(1)若发现杠杆在使用前右端低左端高,要使它在水平位置平衡,可将杠杆左端的平衡螺母向____调节。此后在整个实验过程中,是否还要再旋动两侧的平衡螺母?__________(选填“是”或“否”)。(2)一实验小组得到的两组数据如下表所示:
实验序号 动力F1/N 动力臂l1/cm 阻力F2/N 阻力臂l2/cm
1 2 20 1 10
2 1 8 2 4
这两组数据中,实验序号为_____的一组肯定有错误。经检查,发现是测量动力臂时读错了,动力臂的实际值比记录值大还是小?_______。(3)通过此探究实验应该得出的结论是:____________________________。(4)另一实验小组的同学获得的数据如下表所示:
练习
动力F1/N 动力臂l1/cm 阻力F2/N 阻力臂l2/cm
4 5 5 4
他们得出的结论是:“动力+动力臂=阻力+阻力臂”。你认为他们的实验存在什么问题?_________________________________________________
解答:(1)左;否(2)1;小(3)动力×动力臂=阻力×阻力臂(4)根据一次实验,得出的实验结论不具有普遍性,不同单位的物理量之间不能相加
