7.1 行星的运动 课件(共21张PPT)
文档属性
| 名称 | 7.1 行星的运动 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-08 23:18:03 | ||
图片预览






文档简介
(共21张PPT)
高一物理必修二
7.1行星的运动
浩瀚宇宙,星辰大海,引得古今中外无数佳话。那么在缺少浪漫情怀的科学家眼中,宇宙是什么呢?
迢迢牵牛星,皎皎河汉女;纤纤擢素手,札札弄机抒;终日不成章,泣涕零如雨;河汉清且浅,相去复几许!盈盈一水间,脉脉不得语。
科学家首先观察的是我们所处的太阳系,太阳系中的行星是如何运动的?
4
一、行星运动的两种学说
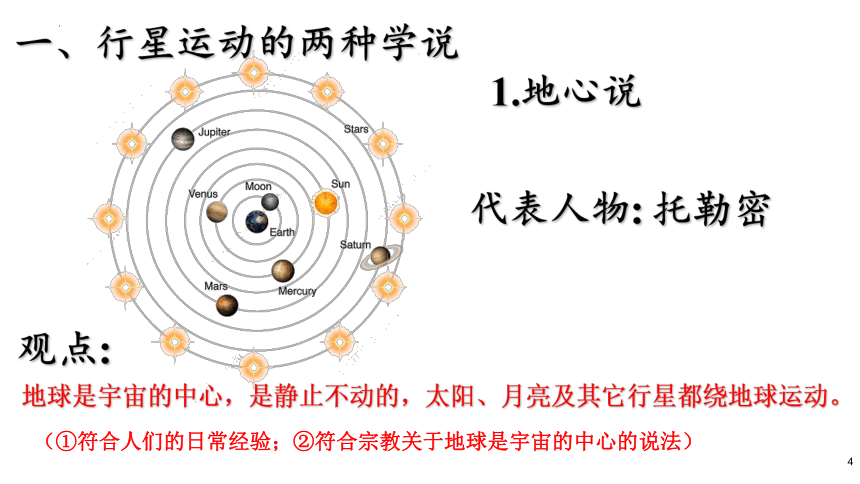
1.地心说
代表人物:
托勒密
观点:
地球是宇宙的中心,是静止不动的,太阳、月亮及其它行星都绕地球运动。
(①符合人们的日常经验;②符合宗教关于地球是宇宙的中心的说法)
5
一、行星运动的两种学说
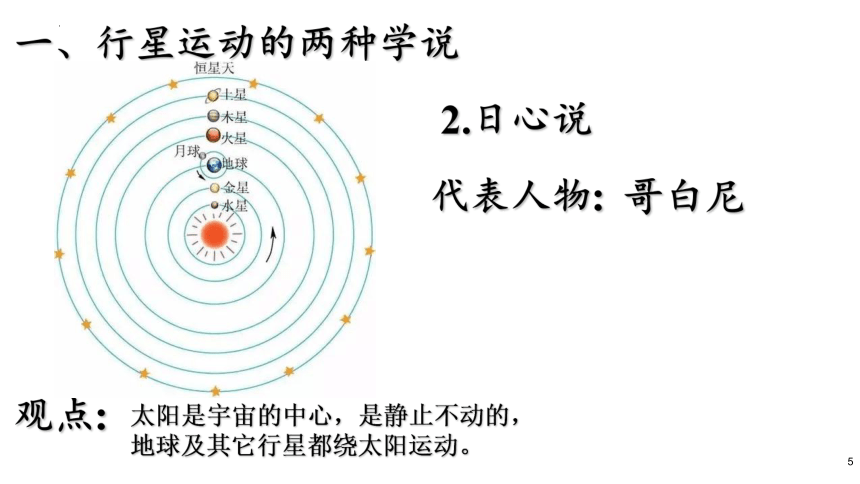
2.日心说
代表人物:
哥白尼
观点:
太阳是宇宙的中心,是静止不动的,
地球及其它行星都绕太阳运动。
现在我们知道,宇宙是没有中心的,是起源于137亿年前的大爆炸。
所以地心说是错误的,日心说相对正确,但是不完善的。
其中日心说中还有一个观点认为“天体的运动时匀速圆周运动”,这些也与事实不符合。
1、丹麦天文学家第谷的探索:
对天体运动进一步的研究
在哥白尼之后,第谷连续20年对行星的位置进行了较仔细的测量,留下了及其丰富的第一手观测资料,并且大大提高了测量的精确程度。
第谷的学生开普勒用二十多年时间研究第谷的行星观测记录,发现并总结得出了有关行星运动非常简洁的三个定律。
约翰尼斯·开普勒:
德国天文学家、数学家与占星家
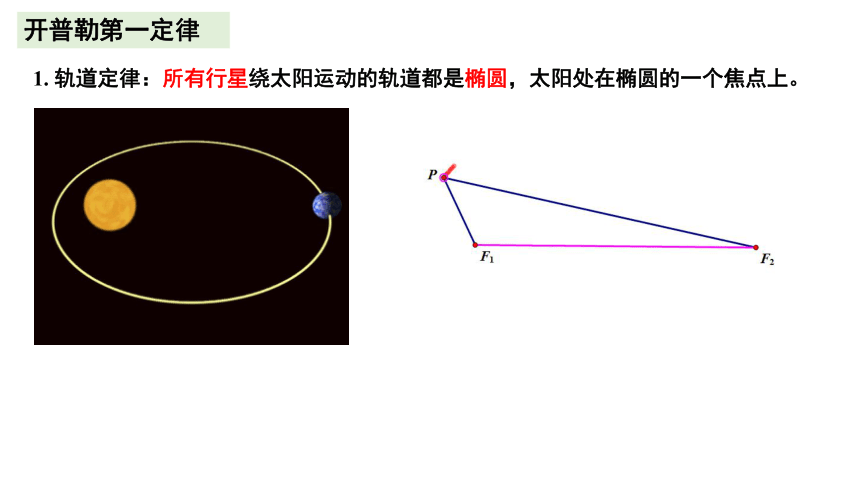
开普勒第一定律
1. 轨道定律:所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
半长轴 a
o
焦点1
半短轴 b
焦点2
(1)行星绕太阳运动的轨道不是圆,是椭圆;
(2)太阳不在椭圆的中心,而是在其中一个焦点上;
(3)行星与太阳的距离是不断变化的.
2. 面积定律:对任意一个行星,它与太阳的连线在相等的时间内扫过的面积相等。
若经相同时间t,行星先后走过1-2的轨迹和3-4的轨迹,因为两块阴影部分的面积相等,故行星离太阳较近的时候(1-2)运行速度较大,而离太阳较远的时候(3-4)速度较小。
开普勒第二定律
从面积定律我们看到,行星在近日点速度快,在远日点速度慢,其实这个问题我们在初中物理中已经利用动能和重力势能的相互转化来作出了定性解释,而面积定律则给出了定量计算的依据,可见我们从不同角度来研究同一个问题,可以加深对问题的理解。
3. 周期定律:
所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。
(1)表达式:
(2)a 代表椭圆轨道的半长轴,
T 代表的公转周期;
(3)k 是一个对所有行星都相同的常数
(k 的大小与行星无关,只与中心天体的质量有关;若中心天体不同,则 k 不同)。
开普勒第三定律
一、行星运动的两种学说
二、开普勒定律
1. 开普勒第一定律(轨道定律):所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
2. 开普勒第二定律(面积定律):对任意一个行星,它与太阳的连线在相等的时间内扫过的面积相等。
3. 开普勒第三定律(周期定律):所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。
也适用于卫星和行星的运动关系
(1)行星绕太阳运动的轨道十分接近圆,太阳处在圆心;
4. 行星运动的近似处理方法:
(2)行星做匀速圆周运动;
(3)所有行星轨道半径 r 的三次方与它公转周期 T 的二次方的比值都相等,即
【即学即用】1.判断下列说法的正误.(1)地球是整个宇宙的中心,其他天体都绕地球运动.( )(2)太阳系中所有行星都绕太阳做椭圆运动,且它们到太阳的距离都相同.( )(3)同一行星沿椭圆轨道绕太阳运动,靠近太阳时速度增大,远离太阳时速度减小.( )(4)行星轨道的半长轴越长,行星的周期越长.( )(5)开普勒第三定律中的常数k与行星无关,与太阳也无关.( )
×
×
×
√
√
如图所示,椭圆为地球绕太阳运动的轨道,A、B两点分别为地球绕太阳运动的近日点(行星距离太阳最近的点)和远日点(行星距离太阳最远的点),地球经过这两点时的速率分别为vA和vB;阴影部分为地球与太阳的连线在相等时间内扫过的面积,分别用SA和SB表示,则vA________vB、SA________SB.(均选填“>”“=”或“<”)
> =
如图所示,某行星沿椭圆轨道运行,远日点离太阳的距离为a,近日点离太阳的距离为b,过远日点时行星的速率为va,则过近日点时行星的速率为( )
典例分析
C
如图所示,火星和地球都在围绕着太阳旋转,其运行轨道是椭圆。根据开普勒行星运动定律可知( )
A.太阳位于地球运行轨道的中心
B.地球靠近太阳的过程中,运行速率减小
C.火星远离太阳的过程中,它与太阳的连
线在相等时间内扫过的面积逐渐增大
D.火星绕太阳运行一周的时间比地球的长
D
若将八大行星绕太阳运行的轨迹粗略认为圆,各星球半径和轨道半径如下图所示,从表中所给数据可以估算海王星的的公转周期最接近( )
A、80年 B、120年 C、 165年 D、200年
C
再见
高一物理必修二
7.1行星的运动
浩瀚宇宙,星辰大海,引得古今中外无数佳话。那么在缺少浪漫情怀的科学家眼中,宇宙是什么呢?
迢迢牵牛星,皎皎河汉女;纤纤擢素手,札札弄机抒;终日不成章,泣涕零如雨;河汉清且浅,相去复几许!盈盈一水间,脉脉不得语。
科学家首先观察的是我们所处的太阳系,太阳系中的行星是如何运动的?
4
一、行星运动的两种学说
1.地心说
代表人物:
托勒密
观点:
地球是宇宙的中心,是静止不动的,太阳、月亮及其它行星都绕地球运动。
(①符合人们的日常经验;②符合宗教关于地球是宇宙的中心的说法)
5
一、行星运动的两种学说
2.日心说
代表人物:
哥白尼
观点:
太阳是宇宙的中心,是静止不动的,
地球及其它行星都绕太阳运动。
现在我们知道,宇宙是没有中心的,是起源于137亿年前的大爆炸。
所以地心说是错误的,日心说相对正确,但是不完善的。
其中日心说中还有一个观点认为“天体的运动时匀速圆周运动”,这些也与事实不符合。
1、丹麦天文学家第谷的探索:
对天体运动进一步的研究
在哥白尼之后,第谷连续20年对行星的位置进行了较仔细的测量,留下了及其丰富的第一手观测资料,并且大大提高了测量的精确程度。
第谷的学生开普勒用二十多年时间研究第谷的行星观测记录,发现并总结得出了有关行星运动非常简洁的三个定律。
约翰尼斯·开普勒:
德国天文学家、数学家与占星家
开普勒第一定律
1. 轨道定律:所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
半长轴 a
o
焦点1
半短轴 b
焦点2
(1)行星绕太阳运动的轨道不是圆,是椭圆;
(2)太阳不在椭圆的中心,而是在其中一个焦点上;
(3)行星与太阳的距离是不断变化的.
2. 面积定律:对任意一个行星,它与太阳的连线在相等的时间内扫过的面积相等。
若经相同时间t,行星先后走过1-2的轨迹和3-4的轨迹,因为两块阴影部分的面积相等,故行星离太阳较近的时候(1-2)运行速度较大,而离太阳较远的时候(3-4)速度较小。
开普勒第二定律
从面积定律我们看到,行星在近日点速度快,在远日点速度慢,其实这个问题我们在初中物理中已经利用动能和重力势能的相互转化来作出了定性解释,而面积定律则给出了定量计算的依据,可见我们从不同角度来研究同一个问题,可以加深对问题的理解。
3. 周期定律:
所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。
(1)表达式:
(2)a 代表椭圆轨道的半长轴,
T 代表的公转周期;
(3)k 是一个对所有行星都相同的常数
(k 的大小与行星无关,只与中心天体的质量有关;若中心天体不同,则 k 不同)。
开普勒第三定律
一、行星运动的两种学说
二、开普勒定律
1. 开普勒第一定律(轨道定律):所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
2. 开普勒第二定律(面积定律):对任意一个行星,它与太阳的连线在相等的时间内扫过的面积相等。
3. 开普勒第三定律(周期定律):所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。
也适用于卫星和行星的运动关系
(1)行星绕太阳运动的轨道十分接近圆,太阳处在圆心;
4. 行星运动的近似处理方法:
(2)行星做匀速圆周运动;
(3)所有行星轨道半径 r 的三次方与它公转周期 T 的二次方的比值都相等,即
【即学即用】1.判断下列说法的正误.(1)地球是整个宇宙的中心,其他天体都绕地球运动.( )(2)太阳系中所有行星都绕太阳做椭圆运动,且它们到太阳的距离都相同.( )(3)同一行星沿椭圆轨道绕太阳运动,靠近太阳时速度增大,远离太阳时速度减小.( )(4)行星轨道的半长轴越长,行星的周期越长.( )(5)开普勒第三定律中的常数k与行星无关,与太阳也无关.( )
×
×
×
√
√
如图所示,椭圆为地球绕太阳运动的轨道,A、B两点分别为地球绕太阳运动的近日点(行星距离太阳最近的点)和远日点(行星距离太阳最远的点),地球经过这两点时的速率分别为vA和vB;阴影部分为地球与太阳的连线在相等时间内扫过的面积,分别用SA和SB表示,则vA________vB、SA________SB.(均选填“>”“=”或“<”)
> =
如图所示,某行星沿椭圆轨道运行,远日点离太阳的距离为a,近日点离太阳的距离为b,过远日点时行星的速率为va,则过近日点时行星的速率为( )
典例分析
C
如图所示,火星和地球都在围绕着太阳旋转,其运行轨道是椭圆。根据开普勒行星运动定律可知( )
A.太阳位于地球运行轨道的中心
B.地球靠近太阳的过程中,运行速率减小
C.火星远离太阳的过程中,它与太阳的连
线在相等时间内扫过的面积逐渐增大
D.火星绕太阳运行一周的时间比地球的长
D
若将八大行星绕太阳运行的轨迹粗略认为圆,各星球半径和轨道半径如下图所示,从表中所给数据可以估算海王星的的公转周期最接近( )
A、80年 B、120年 C、 165年 D、200年
C
再见
