2022年人教版数学七年级下册5.2.1平行线课件(17张)
文档属性
| 名称 | 2022年人教版数学七年级下册5.2.1平行线课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 726.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 15:15:51 | ||
图片预览




文档简介
(共17张PPT)
第五章 相交线与平行线
5.2.1平行线
人教版七年级数学(下册)
议课组:第一组
议课时间:2021.2.22
授课时间:2021.2
1、了解在同一平面内两条直线相交和平行
的位置关系;(重点)
学习目标(1分钟)
2、知道平行公理以及平行公理的推论。(难点)
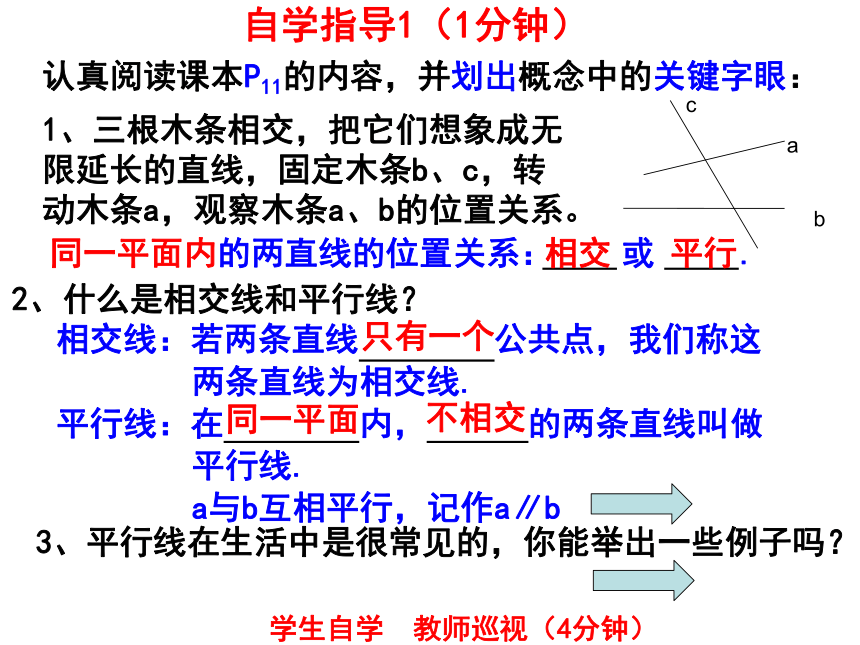
同一平面内的两直线的位置关系: 或 .
相交线:若两条直线 公共点,我们称这
两条直线为相交线.
平行线:在 内, 的两条直线叫做
平行线.
a与b互相平行,记作a∥b
自学指导1(1分钟)
学生自学 教师巡视(4分钟)
认真阅读课本P11的内容,并划出概念中的关键字眼:
2、什么是相交线和平行线?
相交
平行
只有一个
同一平面
不相交
1、三根木条相交,把它们想象成无限延长的直线,固定木条b、c,转动木条a,观察木条a、b的位置关系。
a
b
c
3、平行线在生活中是很常见的,你能举出一些例子吗?
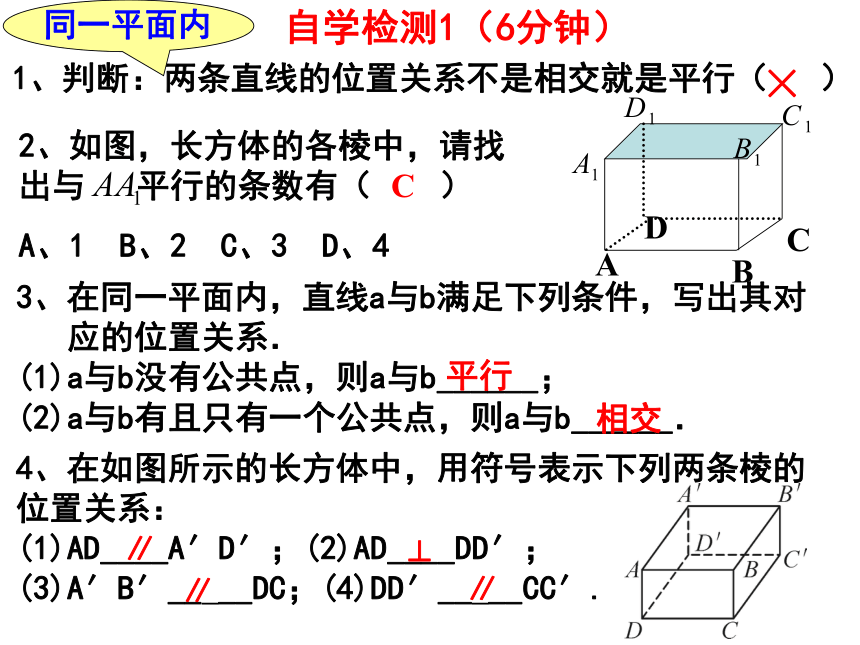
2、如图,长方体的各棱中,请找出与 平行的条数有( )
A、1 B、2 C、3 D、4
1、判断:两条直线的位置关系不是相交就是平行( )
×
自学检测1(6分钟)
同一平面内
C
A
B
C
D
3、在同一平面内,直线a与b满足下列条件,写出其对
应的位置关系.
(1)a与b没有公共点,则a与b______;
(2)a与b有且只有一个公共点,则a与b______.
4、在如图所示的长方体中,用符号表示下列两条棱的
位置关系:
(1)AD____A′D′;(2)AD____DD′;
(3)A′B′__ __DC;(4)DD′__ __CC′.
平行
相交
∥
⊥
∥
∥
自学指导2(1分钟)
认真阅读课本P12的内容, 并划出概念中的关键字眼:
1、在图5.2-1中旋转木条a的过程中,有几个位置使得直线a与b平行?
学生自学 教师巡视(5分钟)
B
C
a
3、平行公理:
平行公理的推论:
经过直线外一点,有且只有一条直线与这条直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
2、如图5.2-3过点B画直线a的平行线,能画几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?
一个位置
一条;平行
如果a∥b,c∥a,那么b∥c
自学检测2(8分钟)
1.下列推理正确的是( )
A.因为a∥b,c∥d,所以b∥d
B.因为a∥c,b∥d,所以c∥d
C.因为a∥b,a∥c,所以b∥c
D.因为a∥b,c∥d,所以a∥c
2.过一点画已知直线的平行线时( )
A.有且只有一条 B.有两条
C.不存在 D.不存在或只有一条
C
D
(课本P12T3)根据语句画出图形:
点P是直线AB外一点,直线CD经过点P,且与直线AB平行。
A
B
P
C
D
解:如图所示
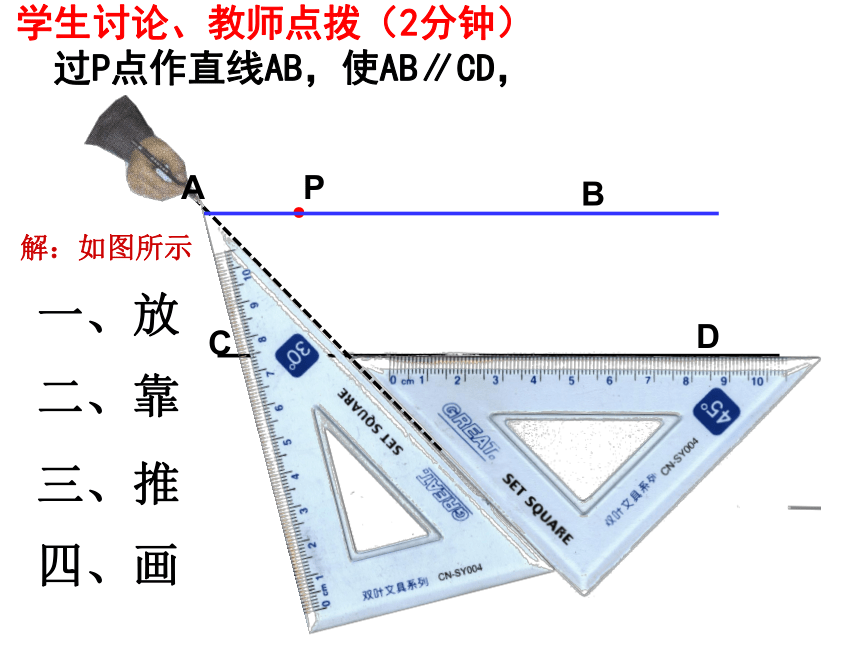
学生讨论、教师点拨(2分钟)
●
一、放
二、靠
三、推
四、画
解:如图所示
P
C
D
A
B
过P点作直线AB,使AB∥CD,
1、在同一平面内,两直线的位置关系 或 .
平行
课堂小结(2分钟)
相交
2、平行公理:
平行公理的推论:
经过直线外一点,有且只有一条直线与这条直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
相交线:若两条直线 公共顶点,我们称这
两条直线为相交线.
平行线:在 内, 的两条直线叫做平行线.
a与b互相平行,记作a∥b
只有一个
同一平面
不相交
如果a∥b,b∥c,那么a∥c
D、在同一平面内,没有公共点的两条直线是平行线
1、(2019春 岱岳区期末)下列说法正确的是( )
D
当堂训练(15分钟)
A、不相交的两直线是平行线
B、在同一平面内,不相交的两条射线是平行线
C、在同一平面内,两条直线不相交就重合
2、下列图形中,AB不平行于CD的是( )
3、在同一平面内有三条直线,它们的交点个数可能是( )
A、0 B、0或3 C、0或1或3 D、0或1或2或3
D
D
5.如图,直线AB,CD是一条河的两岸,并且AB∥CD,点E为直线AB,CD外一点.现想过点E作岸CD的平行线,只需过点E作AB的平行线MN即可,其理由是
______________________________ ___________________________.
6.如图,PC∥AB,QC∥AB,则点P,C,Q在一条直线上,理由是_____________________________________________.
如果两条直线都与第三条直线平行,
那么这两条直线也互相平行
经过直线外一点,有且只有一条直线
与这条直线平行
4.在同一平面内有四条直线a,b,c,d.
(1)若a∥b,b∥c,则a与c的位置关系为_______
(2)若a∥b,a∥c,c∥d,则b与d的位置关系为_______
平行
平行
∥
7.(选做题)完成推理并在括号内填上理由:
解:(1)如图①,∵AB∥CD,EF∥CD,
∴AB____EF(_____________________________ );
(2)如图②,过点F可画EF∥AB (__________________________________________ )
又∵AB∥CD,
∴EF___CD(_____________________________ ).
平行于同一条直线的两条直线平行
过直线外一点,有且只有一条直线与这条直线平行
∥
平行于同一条直线的两条直线平行
正本作业:P12 练习T(2)
板书设计
5.2.1 平行线
1、在同一平面内,两直线的位置关系 或 .
平行
相交
2、平行公理:
3.平行公理的推论:
经过直线外一点,有且只有一条直线与这条直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
相交线:若两条直线 公共顶点,我们称这
两条直线为相交线.
平行线:在 内, 的两条直线叫做
平行线.
a与b互相平行,记作a∥b
只有一个
同一平面
不相交
我们通常用“//”表示平行.
平行线的表示法:
C
D
B
A
·
·
·
·
m∥n
AB∥CD
m
n
读作: “AB平行于CD”
读作: “m平行于n ”
数学来源于生活
第五章 相交线与平行线
5.2.1平行线
人教版七年级数学(下册)
议课组:第一组
议课时间:2021.2.22
授课时间:2021.2
1、了解在同一平面内两条直线相交和平行
的位置关系;(重点)
学习目标(1分钟)
2、知道平行公理以及平行公理的推论。(难点)
同一平面内的两直线的位置关系: 或 .
相交线:若两条直线 公共点,我们称这
两条直线为相交线.
平行线:在 内, 的两条直线叫做
平行线.
a与b互相平行,记作a∥b
自学指导1(1分钟)
学生自学 教师巡视(4分钟)
认真阅读课本P11的内容,并划出概念中的关键字眼:
2、什么是相交线和平行线?
相交
平行
只有一个
同一平面
不相交
1、三根木条相交,把它们想象成无限延长的直线,固定木条b、c,转动木条a,观察木条a、b的位置关系。
a
b
c
3、平行线在生活中是很常见的,你能举出一些例子吗?
2、如图,长方体的各棱中,请找出与 平行的条数有( )
A、1 B、2 C、3 D、4
1、判断:两条直线的位置关系不是相交就是平行( )
×
自学检测1(6分钟)
同一平面内
C
A
B
C
D
3、在同一平面内,直线a与b满足下列条件,写出其对
应的位置关系.
(1)a与b没有公共点,则a与b______;
(2)a与b有且只有一个公共点,则a与b______.
4、在如图所示的长方体中,用符号表示下列两条棱的
位置关系:
(1)AD____A′D′;(2)AD____DD′;
(3)A′B′__ __DC;(4)DD′__ __CC′.
平行
相交
∥
⊥
∥
∥
自学指导2(1分钟)
认真阅读课本P12的内容, 并划出概念中的关键字眼:
1、在图5.2-1中旋转木条a的过程中,有几个位置使得直线a与b平行?
学生自学 教师巡视(5分钟)
B
C
a
3、平行公理:
平行公理的推论:
经过直线外一点,有且只有一条直线与这条直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
2、如图5.2-3过点B画直线a的平行线,能画几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?
一个位置
一条;平行
如果a∥b,c∥a,那么b∥c
自学检测2(8分钟)
1.下列推理正确的是( )
A.因为a∥b,c∥d,所以b∥d
B.因为a∥c,b∥d,所以c∥d
C.因为a∥b,a∥c,所以b∥c
D.因为a∥b,c∥d,所以a∥c
2.过一点画已知直线的平行线时( )
A.有且只有一条 B.有两条
C.不存在 D.不存在或只有一条
C
D
(课本P12T3)根据语句画出图形:
点P是直线AB外一点,直线CD经过点P,且与直线AB平行。
A
B
P
C
D
解:如图所示
学生讨论、教师点拨(2分钟)
●
一、放
二、靠
三、推
四、画
解:如图所示
P
C
D
A
B
过P点作直线AB,使AB∥CD,
1、在同一平面内,两直线的位置关系 或 .
平行
课堂小结(2分钟)
相交
2、平行公理:
平行公理的推论:
经过直线外一点,有且只有一条直线与这条直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
相交线:若两条直线 公共顶点,我们称这
两条直线为相交线.
平行线:在 内, 的两条直线叫做平行线.
a与b互相平行,记作a∥b
只有一个
同一平面
不相交
如果a∥b,b∥c,那么a∥c
D、在同一平面内,没有公共点的两条直线是平行线
1、(2019春 岱岳区期末)下列说法正确的是( )
D
当堂训练(15分钟)
A、不相交的两直线是平行线
B、在同一平面内,不相交的两条射线是平行线
C、在同一平面内,两条直线不相交就重合
2、下列图形中,AB不平行于CD的是( )
3、在同一平面内有三条直线,它们的交点个数可能是( )
A、0 B、0或3 C、0或1或3 D、0或1或2或3
D
D
5.如图,直线AB,CD是一条河的两岸,并且AB∥CD,点E为直线AB,CD外一点.现想过点E作岸CD的平行线,只需过点E作AB的平行线MN即可,其理由是
______________________________ ___________________________.
6.如图,PC∥AB,QC∥AB,则点P,C,Q在一条直线上,理由是_____________________________________________.
如果两条直线都与第三条直线平行,
那么这两条直线也互相平行
经过直线外一点,有且只有一条直线
与这条直线平行
4.在同一平面内有四条直线a,b,c,d.
(1)若a∥b,b∥c,则a与c的位置关系为_______
(2)若a∥b,a∥c,c∥d,则b与d的位置关系为_______
平行
平行
∥
7.(选做题)完成推理并在括号内填上理由:
解:(1)如图①,∵AB∥CD,EF∥CD,
∴AB____EF(_____________________________ );
(2)如图②,过点F可画EF∥AB (__________________________________________ )
又∵AB∥CD,
∴EF___CD(_____________________________ ).
平行于同一条直线的两条直线平行
过直线外一点,有且只有一条直线与这条直线平行
∥
平行于同一条直线的两条直线平行
正本作业:P12 练习T(2)
板书设计
5.2.1 平行线
1、在同一平面内,两直线的位置关系 或 .
平行
相交
2、平行公理:
3.平行公理的推论:
经过直线外一点,有且只有一条直线与这条直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
相交线:若两条直线 公共顶点,我们称这
两条直线为相交线.
平行线:在 内, 的两条直线叫做
平行线.
a与b互相平行,记作a∥b
只有一个
同一平面
不相交
我们通常用“//”表示平行.
平行线的表示法:
C
D
B
A
·
·
·
·
m∥n
AB∥CD
m
n
读作: “AB平行于CD”
读作: “m平行于n ”
数学来源于生活
