2022年人教版数学七年级下册5.2.2平行线的判定课件(19张)
文档属性
| 名称 | 2022年人教版数学七年级下册5.2.2平行线的判定课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 203.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 15:16:22 | ||
图片预览





文档简介
(共19张PPT)
1、在同一平面内,两直线的位置关系 或 .
平行
课前提问(1分钟)
相交
2、平行公理:
3、平行公理的推论:
经过直线外一点,有且只有一条直线与这条直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
如果a∥b,b∥c,那么a∥c
第五章 相交线与平行线
5.2.2平行线判定
人教版七年级数学(下册)
议课组:第一组
议课时间:2022.3.5
授课时间:2022.3.
1、探索并掌握两条直线平行的判定条件(重点)
2、应用平行线的判定定理解决一些实际问题(难点)
学习目标(1分钟)
自学指导1(1分钟)
学生自学 教师巡视(5分钟)
认真阅读课本P12-14例题之前的内容,回答问题并划出概念中的关键字眼:
判定两直线平行的方法
判定方法1:
判定方法2:
判定方法3:
简单说成:同位角相等,两直线平行
简单说成:内错角相等,两直线平行
简单说成:同旁内角互补,两直线平行
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
自学检测1 (6分钟)
2、看图2填空:
∵∠2=∠4(已知)
∴ ∥ ( )
∵∠2= ∠1 (已知)
∴ ∥ (内错角相等,两直线平行)
∵∠3+∠4=180°(已知)
∴ ∥ ( )
FG
DE
AC
DE
DE
FG
同旁内角互补,两直线平行
同位角相等,两直线平行
1
2
3
4
A
B
C
D
E
F
G
1、(2020惠州中考)如图1,下列条件不能判定直线a∥b的是( )
A.∠1=∠2 B.∠1=∠3
C.∠1+∠4=180° D.∠2+∠4=180°
C
图1
图2
要根据已知条件,选定同位角相等或内错角相等或同旁内角互补,来判断两直线平行.
自学指导2(1分钟)
认真阅读课本P14的例题, 并思考下面问题:
学生自学 教师巡视(6分钟)
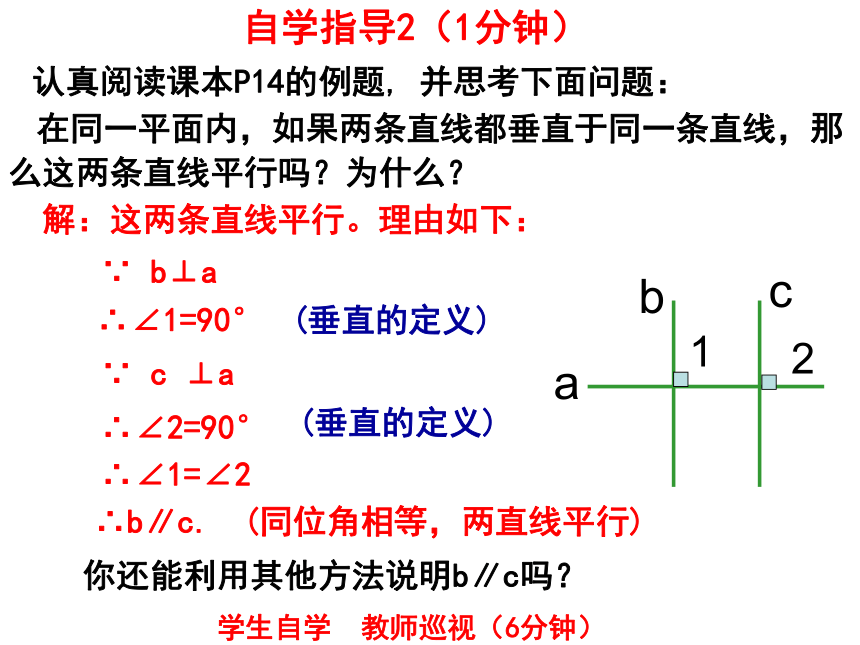
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
解:这两条直线平行。理由如下:
a
b
c
1
2
∵ b⊥a
∴∠2=90°
(垂直的定义)
∴b∥c.
(同位角相等,两直线平行)
∴∠1=90°
(垂直的定义)
∵ c ⊥a
∴∠1=∠2
你还能利用其他方法说明b∥c吗?
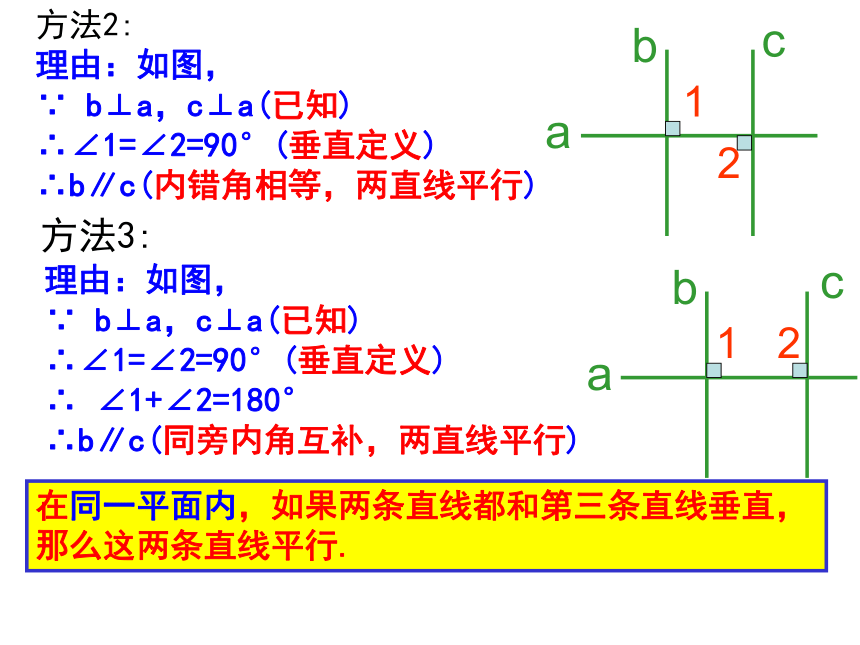
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
方法2:
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
方法3:
在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行.
自学检测2(6分钟)
如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD平行于EF吗?为什么?
解:CD∥EF.理由如下:
∵AB⊥BD,CD⊥BD
∴∠B=90°,∠D=90°
∴∠B+∠D=180°
∴AB∥CD(同旁内角互补,两直线平行)
∵∠1+∠2=180°
∴AB∥EF(同旁内角互补,两直线平行)
∴CD∥EF(平行于同一条直线的两直线平行)
2.(课本P17T12)如图,当∠1=∠3时,直线a,b平行吗?当∠2+∠3=180°时,直线a,b平行吗?为什么
∵∠1+∠2=180°,∠3+∠4=180°,∠1=∠3,
∵∠3+∠4=180°,∠2+∠3=180°,
∴∠2=∠4,
∴a∥b.
当∠2+∠3=180°时,a∥b.理由如下:
∴∠2=∠4,
∴a∥b.
学生讨论、教师点拨(2分钟)
判定两条直线是否平行的方法有:
1.同位角相等,两直线平行.
2.内错角相等,两直线平行.
3.同旁内角互补,两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.在同一平面内,如果两条直线都与第三条直线垂直,那么这两条直线也互相平行.
6.平行线的定义.
课堂小结(2分钟)
1
2
a
A
B
C
D
1、同位角相等,两直线平行.
几何语言:
∴ AB∥CD (同位角相等,两直线平行)
∵ ∠1 = ∠2
2、内错角相等,两直线平行.
几何语言:
∵ ∠1= ∠2
∴ AB∥CD(内错角相等,两直线平行)
1
2
A
B
C
D
a
3、同旁内角互补,两直线平行.
几何语言:
∵ ∠1+∠2=180 °
∴ AB∥CD (同旁内角互补,两直线平行)
1
2
A
B
C
D
a
4、在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行.
当堂训练(15分钟)
1、请你根据右图填空
(1)∵∠1=∠3,∴_____∥______
(________角相等,两直线平行).
(2)∵∠2=∠5,∴______∥______
(________角相等,两直线平行).
(3)∵∠3+∠4=180°,∴_____∥______
(________角互补,两直线平行).
(4)∵EF⊥FB,CD⊥FB,∴______∥_____
(_ _______于同一条直线的两直线平行).
(5)∵EF∥AB,CD∥AB,∴_____∥____
(________于同一条直线的两直线平行).
AB
CD
同位
AB
CD
内错
EF
CD
同旁内
EF
CD
在同一平面内,垂直
EF
CD
平行
3、(2020广州中考)如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A、∠3=∠4 B、∠1=∠2
C、∠D=∠DCE D、∠D+∠ACD=180°
B
5、(变式题)下列说法中正确的有( )
①同位角相等;②若a∥b,b∥c,则a∥c;③过一点有且只有一条直线与已知直线平行;④两直线的位置关系只有相交与平行.
A、0个 B、1个 C、2个 D、3个
B
2.如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗?_______.(填“合格”或“不合格”)
合格
4、 三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( )
A.a⊥b B.a∥b C.a⊥b或a∥b D.无法确定
B
∴AB∥CD.(内错角相等,两直线平行)
6、(选做题)如图所示,已知
∠BED=∠B+∠D,试说明AB与
CD的位置关系.
(正本作业) 课本P15 习题 5.2 T4
5、如图,BD平分∠ABC, ∠1= ∠D,那么AB与CD平行吗?
解:AB与CD平行.理由如下:
∵BD平分∠ABC.(已知)
∴∠ABD=∠1.(角平分线的定义)
又∵∠1=∠D.(已知)
∴∠ABD=∠D.(等量代换)
解:AB∥CD;理由如下:
如图,过点E作∠BEF=∠B
∴AB∥EF(内错角相等,两直线平行),
∵∠BED=∠BEF+∠FED
=∠B +∠D(已知),
∠BEF=∠B(已作),
∴∠FED=∠D,
∴CD//EF(内错角相等,两直线平行)
∴AB//CD(平行于同一条直线的两条直线平行)
(选做题)如图所示,已知∠BED=∠B+∠D,试说明AB与CD的位置关系.
1
2
a
A
B
C
D
1、同位角相等,两直线平行.
几何语言:
∴ AB∥CD (同位角相等,两直线平行)
∵ ∠1 = ∠2
2、内错角相等,两直线平行.
几何语言:
∵ ∠1= ∠2
∴ AB∥CD(内错角相等,两直线平行)
1
2
A
B
C
D
a
3、同旁内角互补,两直线平行.
几何语言:
∵ ∠1+∠2=180 °
∴ AB∥CD (同旁内角互补,两直线平行)
1
2
A
B
C
D
a
板书设计
5.2.2 平行线判定
4、在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行.
1
2
a
A
B
C
D
同位角相等,两直线平行.
几何语言:
∴ AB∥CD (同位角相等,两直线平行)
∵ ∠1 = ∠2
两直线平行的判定方法(1):
内错角相等,两直线平行.
几何语言:
∵ ∠1= ∠2
∴ AB∥CD(内错角相等,两直线平行)
1
2
A
B
C
D
a
两直线平行的判定方法(2):
同旁内角互补,两直线平行.
几何语言:
∵ ∠1+∠2=180 °
∴ AB∥CD (同旁内角互补,两直线平行)
1
2
A
B
C
D
a
两直线平行的判定方法(3):
1、在同一平面内,两直线的位置关系 或 .
平行
课前提问(1分钟)
相交
2、平行公理:
3、平行公理的推论:
经过直线外一点,有且只有一条直线与这条直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
如果a∥b,b∥c,那么a∥c
第五章 相交线与平行线
5.2.2平行线判定
人教版七年级数学(下册)
议课组:第一组
议课时间:2022.3.5
授课时间:2022.3.
1、探索并掌握两条直线平行的判定条件(重点)
2、应用平行线的判定定理解决一些实际问题(难点)
学习目标(1分钟)
自学指导1(1分钟)
学生自学 教师巡视(5分钟)
认真阅读课本P12-14例题之前的内容,回答问题并划出概念中的关键字眼:
判定两直线平行的方法
判定方法1:
判定方法2:
判定方法3:
简单说成:同位角相等,两直线平行
简单说成:内错角相等,两直线平行
简单说成:同旁内角互补,两直线平行
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
自学检测1 (6分钟)
2、看图2填空:
∵∠2=∠4(已知)
∴ ∥ ( )
∵∠2= ∠1 (已知)
∴ ∥ (内错角相等,两直线平行)
∵∠3+∠4=180°(已知)
∴ ∥ ( )
FG
DE
AC
DE
DE
FG
同旁内角互补,两直线平行
同位角相等,两直线平行
1
2
3
4
A
B
C
D
E
F
G
1、(2020惠州中考)如图1,下列条件不能判定直线a∥b的是( )
A.∠1=∠2 B.∠1=∠3
C.∠1+∠4=180° D.∠2+∠4=180°
C
图1
图2
要根据已知条件,选定同位角相等或内错角相等或同旁内角互补,来判断两直线平行.
自学指导2(1分钟)
认真阅读课本P14的例题, 并思考下面问题:
学生自学 教师巡视(6分钟)
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
解:这两条直线平行。理由如下:
a
b
c
1
2
∵ b⊥a
∴∠2=90°
(垂直的定义)
∴b∥c.
(同位角相等,两直线平行)
∴∠1=90°
(垂直的定义)
∵ c ⊥a
∴∠1=∠2
你还能利用其他方法说明b∥c吗?
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
方法2:
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
方法3:
在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行.
自学检测2(6分钟)
如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD平行于EF吗?为什么?
解:CD∥EF.理由如下:
∵AB⊥BD,CD⊥BD
∴∠B=90°,∠D=90°
∴∠B+∠D=180°
∴AB∥CD(同旁内角互补,两直线平行)
∵∠1+∠2=180°
∴AB∥EF(同旁内角互补,两直线平行)
∴CD∥EF(平行于同一条直线的两直线平行)
2.(课本P17T12)如图,当∠1=∠3时,直线a,b平行吗?当∠2+∠3=180°时,直线a,b平行吗?为什么
∵∠1+∠2=180°,∠3+∠4=180°,∠1=∠3,
∵∠3+∠4=180°,∠2+∠3=180°,
∴∠2=∠4,
∴a∥b.
当∠2+∠3=180°时,a∥b.理由如下:
∴∠2=∠4,
∴a∥b.
学生讨论、教师点拨(2分钟)
判定两条直线是否平行的方法有:
1.同位角相等,两直线平行.
2.内错角相等,两直线平行.
3.同旁内角互补,两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.在同一平面内,如果两条直线都与第三条直线垂直,那么这两条直线也互相平行.
6.平行线的定义.
课堂小结(2分钟)
1
2
a
A
B
C
D
1、同位角相等,两直线平行.
几何语言:
∴ AB∥CD (同位角相等,两直线平行)
∵ ∠1 = ∠2
2、内错角相等,两直线平行.
几何语言:
∵ ∠1= ∠2
∴ AB∥CD(内错角相等,两直线平行)
1
2
A
B
C
D
a
3、同旁内角互补,两直线平行.
几何语言:
∵ ∠1+∠2=180 °
∴ AB∥CD (同旁内角互补,两直线平行)
1
2
A
B
C
D
a
4、在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行.
当堂训练(15分钟)
1、请你根据右图填空
(1)∵∠1=∠3,∴_____∥______
(________角相等,两直线平行).
(2)∵∠2=∠5,∴______∥______
(________角相等,两直线平行).
(3)∵∠3+∠4=180°,∴_____∥______
(________角互补,两直线平行).
(4)∵EF⊥FB,CD⊥FB,∴______∥_____
(_ _______于同一条直线的两直线平行).
(5)∵EF∥AB,CD∥AB,∴_____∥____
(________于同一条直线的两直线平行).
AB
CD
同位
AB
CD
内错
EF
CD
同旁内
EF
CD
在同一平面内,垂直
EF
CD
平行
3、(2020广州中考)如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A、∠3=∠4 B、∠1=∠2
C、∠D=∠DCE D、∠D+∠ACD=180°
B
5、(变式题)下列说法中正确的有( )
①同位角相等;②若a∥b,b∥c,则a∥c;③过一点有且只有一条直线与已知直线平行;④两直线的位置关系只有相交与平行.
A、0个 B、1个 C、2个 D、3个
B
2.如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗?_______.(填“合格”或“不合格”)
合格
4、 三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( )
A.a⊥b B.a∥b C.a⊥b或a∥b D.无法确定
B
∴AB∥CD.(内错角相等,两直线平行)
6、(选做题)如图所示,已知
∠BED=∠B+∠D,试说明AB与
CD的位置关系.
(正本作业) 课本P15 习题 5.2 T4
5、如图,BD平分∠ABC, ∠1= ∠D,那么AB与CD平行吗?
解:AB与CD平行.理由如下:
∵BD平分∠ABC.(已知)
∴∠ABD=∠1.(角平分线的定义)
又∵∠1=∠D.(已知)
∴∠ABD=∠D.(等量代换)
解:AB∥CD;理由如下:
如图,过点E作∠BEF=∠B
∴AB∥EF(内错角相等,两直线平行),
∵∠BED=∠BEF+∠FED
=∠B +∠D(已知),
∠BEF=∠B(已作),
∴∠FED=∠D,
∴CD//EF(内错角相等,两直线平行)
∴AB//CD(平行于同一条直线的两条直线平行)
(选做题)如图所示,已知∠BED=∠B+∠D,试说明AB与CD的位置关系.
1
2
a
A
B
C
D
1、同位角相等,两直线平行.
几何语言:
∴ AB∥CD (同位角相等,两直线平行)
∵ ∠1 = ∠2
2、内错角相等,两直线平行.
几何语言:
∵ ∠1= ∠2
∴ AB∥CD(内错角相等,两直线平行)
1
2
A
B
C
D
a
3、同旁内角互补,两直线平行.
几何语言:
∵ ∠1+∠2=180 °
∴ AB∥CD (同旁内角互补,两直线平行)
1
2
A
B
C
D
a
板书设计
5.2.2 平行线判定
4、在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行.
1
2
a
A
B
C
D
同位角相等,两直线平行.
几何语言:
∴ AB∥CD (同位角相等,两直线平行)
∵ ∠1 = ∠2
两直线平行的判定方法(1):
内错角相等,两直线平行.
几何语言:
∵ ∠1= ∠2
∴ AB∥CD(内错角相等,两直线平行)
1
2
A
B
C
D
a
两直线平行的判定方法(2):
同旁内角互补,两直线平行.
几何语言:
∵ ∠1+∠2=180 °
∴ AB∥CD (同旁内角互补,两直线平行)
1
2
A
B
C
D
a
两直线平行的判定方法(3):
