2022版新教材高中数学第二章平面解析几何章末总结课件新人教B版选择性必修第一册(共52张PPT)
文档属性
| 名称 | 2022版新教材高中数学第二章平面解析几何章末总结课件新人教B版选择性必修第一册(共52张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 10:06:02 | ||
图片预览











文档简介
(共52张PPT)
第二章 平面解析几何
章末总结
题型1 直线的方程
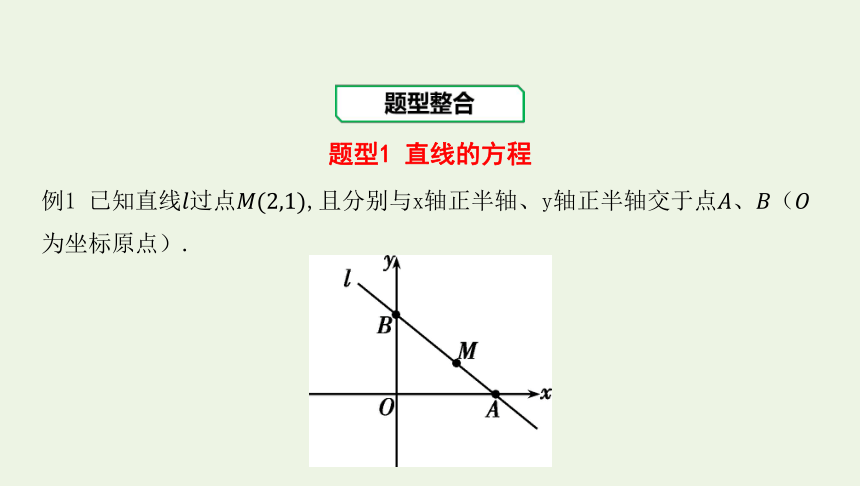
例1 已知直线过点,且分别与x轴正半轴、y轴正半轴交于点、(为坐标原点).
(1) 当的面积为4时,求直线的一般式方程;
[答案] 由题意,设直线l的方程为,
则则
因为直线过点(2,1),所以,所以,
所以直线的方程为,即.
[答案] 设直线的方程为,则(,0),
所以
(2) 当取最小值时,求直线的一般式方程.
所以,
当且仅当时,等号成立,
所以当取最小值时,(正值舍去),
此时直线方程为,即.
方法归纳
求直线方程时常用以下两种方法:
(1)直接法:直接选取适当的直线方程的形式,写出结果.
(2)待定系数法:先以直线满足的某个条件为基础设出直线方程,再由直线满足的另一个条件求出待定系数,从而求得方程.
1. [2021山东青岛二中期末] 已知定点.
(1) 若直线经过点且与直线垂直,求直线的方程;
[答案] 设与直线垂直的直线的方程为,
把代入,得,解得,所以直线的方程为.
(2) 若直线经过点且坐标原点到直线的距离等于3,求直线的方程.
[答案] 当直线的斜率不存在时,直线的方程为,符合题意;
当直线的斜率存在时,设直线的方程为,
即,原点到直线的距离,解得,
所以直线的方程为,即.
综上,直线的方程为或.
题型2 直线与圆
例2 [2020山东烟台高二期中] 已知圆.
(1) 在以下两个问题中任选一个作答.
①已知不过原点的直线与圆相切,且直线在轴、轴上的截距相等,求直线的方程;
②从圆外一点向圆引切线,求切线方程;
[答案] [解析] 圆 的方程可变形为 圆心 的坐标为(-1,2),半径为3.
选择①:直线在两坐标轴上的截距相等且不为零,
直线的斜率为-1.
设直线的方程,又直线与圆相切,
,整理得,∴所求直线的方程为或.
所以直线是圆的切线;
当过的直线的斜率存在时,设切线方程为,
即,由,
得,切线方程为,即.
综上所述,切线方程为或.
选择②:当过 的直线的斜率不存在时,直线方程为 ,
此时圆 到直线的距离为3,
(2) 若圆与圆相交于两点,求线段的长.
[答案] 联立得得
得
.
方法归纳
(1)判断直线与圆的位置关系以几何法为主,解题时应充分利用圆的几何性质简化解题过程.直线和圆相切时,可以利用圆与直线联立的方程组有一组实数解,或者利用圆心到直线的距离等于圆的半径求得参数,有时利用后面方法计算,运算量较小.
(2)解决圆与圆的位置关系的关键是抓住它的几何特征,利用两圆圆心距与两圆半径的和、差的绝对值的大小来确定两圆的位置关系,充分利用几何图形的直观性来分析问题.
2. [2021北京昌平一中高二期中] 已知圆C的圆心在x轴上,且经过点.
(1) 求线段的垂直平分线的方程;
[答案] 设的中点为,则.
由圆的性质,得,所以所以.
所以线段的垂直平分线的方程是.
(2) 求圆的标准方程;
[答案] 设圆的标准方程为其中为半径.
由圆的性质,知圆心在直线上,所以圆心为,
所以圆的标准方程为.
[答案] 设为的中点,则线段,则圆心C到直线的距离,
故,解得,所以直线的方程为.
(3) 已知直线:与圆相交于两点,且=,求直线的方程.
题型3 圆锥曲线的定义与方程
例3
(1) [2020广东实验中学高二月考] 已知椭圆 的左、右焦点分别为过的直线交椭圆于两点,若的最大值为5,则的值为( )
A. 1 B. C. D.
C
[解析] 因为,所以椭圆的焦点在轴上,可知,
因为过的直线交椭圆于两点,所以由椭圆的定义知,,
所以,
当轴时,最小,的值最大,
此时所以解得(负值舍去),故选C.
(2) 过双曲线:的左焦点作斜率为的直线,恰好与圆相切,的右顶点为,且,则双曲线的标准方程为( )
A. B.
C. D.
B
[解析] 设,则直线的方程为,即,
因为直线恰好与圆相切,
所以圆心(0,0)到直线的距离等于半径,即
则,
解得,所以,则.所以双曲线的标准方程为.
方法归纳
(1)研究有关两点的距离的最值问题时,常用定义把曲线上的点到焦点的距离转化为到另一焦点的距离或利用定义把曲线上的点到焦点的距离转化为到准线的距离,再结合几何图形,利用几何意义去解决最值的有关问题.
(2)确定双曲线或椭圆的标准方程需要一个“定位”条件,两个“定量”条件,“定位”是指确定焦点在哪条坐标轴上,“定量”是指确定的值,常用待定系数法求得.
3. 已知椭圆的焦距为2,右顶点为,过原点与轴不重合的直线交于两点,线段的中点为,若直线经过的右焦点,则的方程为( )
A. B.
C. D.
C
[解析] 由题意知,设点,
则
因为直线经过点,所以,
因为,所以,所以,
解得所以所以椭圆的方程为.
题型4 圆锥曲线的性质
例4
(1) [2020山东实验中学高二月考] 已知双曲线的左、右焦点分别为,以线段为直径的圆与双曲线在第二象限的交点为,若直线与圆:相切,则双曲线的渐近线方程是( )
A. y= B. y= C. y= D. y=
A
[解析] 设直线与圆相切于点.如图.
因为是以圆的直径为斜边的圆的内接三角形,所以.
又因为圆与直线的切点为,所以.
又所以则
则因此有.
所以,因此渐近线的方程为.
(2) [2020四川成都高二期中] 已知椭圆的右焦点为,短轴的上端点为,直线交椭圆于两点.若,点到直线的距离不小于,则椭圆的离心率的取值范围是( )
A. (0,] B. (0,]
C. [,1) D. [,1)
A
[解析] 取椭圆的左焦点,连接,如图,根据对称性有,
故四边形为平行四边形,,则,
由点到的距离得
所以故e的取值范围是.
方法归纳
(1)圆锥曲线的性质问题的常见具体类型:①已知基本量求离心率或求离心率的取值范围;②已知圆锥曲线的方程求参数的取值范围;③已知曲线的某些性质求曲线方程或求曲线的其他性质.
(2)解圆锥曲线的性质问题时,一般要灵活地应用圆锥曲线的定义、方程及其图形.
4. 已知双曲线:的左、右焦点分别为点是右支上一点,连接与轴交于点若为坐标原点),则双曲线的渐近线方程为( )
A. B.
C. D.
C
[解析] 设易知与相似,由,
得即
又因为,所以,
所以所以双曲线的渐近线方程为.
5. 若椭圆的左、右焦点分别为,线段被抛物线的焦点分成5:3的两段,则椭圆的离心率为( )
A. B. C. D.
D
[解析] 由题意知,
抛物线的焦点为,由题意可得,解得,又由可得所以.
题型5 直线与圆锥曲线的综合问题
例5 [2021山东聊城一中期中] 已知椭圆的中心在原点,焦点在轴上,离心率为,且经过点,直线交椭圆于不同的两点.
(1) 求椭圆的方程;
[答案] 设椭圆的方程为,因为所以又因为所以故椭圆的方程为.
(2) 求的取值范围;
[答案] 将代入,消去整理得,解得,即的取值范围是(-5,5).
(3) 若直线不过点,试问直线的斜率之和是不是定值,若是定值,求出定值;若不是定值,说明理由.
[答案] 是定值.设直线的斜率分别为,
设由(2)知
则
分子,所以直线的斜率之和是定值0.
方法归纳
直线与圆锥曲线的综合问题,主要包括直线与圆锥曲线位置关系的判断问题、弦长问题、面积问题、定点与定值问题等,求解这类问题时,通常采用代数方法,将直线方程与圆锥曲线的方程联立,消去其中一个未知量,通过讨论所得方程的根的情况来确定位置关系,同时,还经常利用根与系数的关系,采取“设而不求”的办法求解弦长问题、面积问题.
6. 设抛物线:的焦点为,过且斜率为1的直线与交于两点,.
(1) 求抛物线和直线的方程;
[答案] 由题意得,直线l的方程为.
设,,联立消去可得
故.
所以,
解得,因此抛物线的方程是,直线的方程为.
(2) 设点是轴上的一点,且的面积为,求点的坐标.
[答案] 设,点到直线的距离为,则,
又,所以,
所以,解得,
故点的坐标为(5,0)或(-3,0).
1. [2020课标Ⅲ文,8,5分] 点(0,-1)到直线距离的最大值为
( )
A. 1 B. C. D. 2
B
[解析] 由可知直线过定点,
设,
当直线与垂直时,点到直线距离最大,此时.
2. [2020课标Ⅲ理,5,5分] 设为坐标原点,直线与抛物线:交于两点,若,则的焦点坐标为( )
A. B. C. (1,0) D. (2,0)
B
[解析] 因为直线与抛物线交于两点,且,
根据抛物线的对称性可以确定14,
所以(不妨设在第一象限),
代入抛物线方程得,得,所以焦点坐标为,故选B.
3. [2020课标Ⅱ理,5,5分] 若过点(2,1)的圆与两坐标轴都相切,则圆心到直线的距离为( )
A. B. C. D.
B
[解析] 因为圆上的点(2,1)在第一象限,若圆心不在第一象限,则圆至少与一条坐标轴相交,不符合题意,所以圆心必在第一象限,设圆心的坐标为,则圆的半径为,圆的标准方程为.由题意可得,可得,解得,所以圆心的坐标为(1,1)或(5,5),圆心到直线的距离.
4. [2020课标Ⅲ理,11,5分] 设双曲线:的左、右焦点分别为离心率为是上一点,且.若的面积为4,则( )
A. 1 B. 2 C. 4 D. 8
A
[解析] ,,又,即解得(负值舍去),故选A.
5. [2020新高考Ⅰ,9,5分] (多选)已知曲线:.( )
A. 若,则是椭圆,其焦点在轴上
B. 若,则是圆,其半径为
C. 若,则是双曲线,其渐近线方程为
D. 若,,则是两条直线
ACD
[解析] 对于,若,则可化为,因为,所以,即曲线表示焦点在y轴上的椭圆,故选项A正确;对于若则可化为此时曲线表示圆心在原点,半径为的圆,故选项B不正确;对于若则可化为此时曲线表示双曲线,由可得
,故选项C正确;对于D,若则可化为即,此时曲线表示平行于x轴的两条直线,故选项D正确,故选ACD.
6. [2020课标Ⅰ理,15,5分] 已知为双曲线:的右焦点,为的右顶点,为上的点,且垂直于轴.若的斜率为3,则的离心率为____.
2
[解析] 依题可得,,而即变形得,化简可得,解得或(舍去).
第二章 平面解析几何
章末总结
题型1 直线的方程
例1 已知直线过点,且分别与x轴正半轴、y轴正半轴交于点、(为坐标原点).
(1) 当的面积为4时,求直线的一般式方程;
[答案] 由题意,设直线l的方程为,
则则
因为直线过点(2,1),所以,所以,
所以直线的方程为,即.
[答案] 设直线的方程为,则(,0),
所以
(2) 当取最小值时,求直线的一般式方程.
所以,
当且仅当时,等号成立,
所以当取最小值时,(正值舍去),
此时直线方程为,即.
方法归纳
求直线方程时常用以下两种方法:
(1)直接法:直接选取适当的直线方程的形式,写出结果.
(2)待定系数法:先以直线满足的某个条件为基础设出直线方程,再由直线满足的另一个条件求出待定系数,从而求得方程.
1. [2021山东青岛二中期末] 已知定点.
(1) 若直线经过点且与直线垂直,求直线的方程;
[答案] 设与直线垂直的直线的方程为,
把代入,得,解得,所以直线的方程为.
(2) 若直线经过点且坐标原点到直线的距离等于3,求直线的方程.
[答案] 当直线的斜率不存在时,直线的方程为,符合题意;
当直线的斜率存在时,设直线的方程为,
即,原点到直线的距离,解得,
所以直线的方程为,即.
综上,直线的方程为或.
题型2 直线与圆
例2 [2020山东烟台高二期中] 已知圆.
(1) 在以下两个问题中任选一个作答.
①已知不过原点的直线与圆相切,且直线在轴、轴上的截距相等,求直线的方程;
②从圆外一点向圆引切线,求切线方程;
[答案] [解析] 圆 的方程可变形为 圆心 的坐标为(-1,2),半径为3.
选择①:直线在两坐标轴上的截距相等且不为零,
直线的斜率为-1.
设直线的方程,又直线与圆相切,
,整理得,∴所求直线的方程为或.
所以直线是圆的切线;
当过的直线的斜率存在时,设切线方程为,
即,由,
得,切线方程为,即.
综上所述,切线方程为或.
选择②:当过 的直线的斜率不存在时,直线方程为 ,
此时圆 到直线的距离为3,
(2) 若圆与圆相交于两点,求线段的长.
[答案] 联立得得
得
.
方法归纳
(1)判断直线与圆的位置关系以几何法为主,解题时应充分利用圆的几何性质简化解题过程.直线和圆相切时,可以利用圆与直线联立的方程组有一组实数解,或者利用圆心到直线的距离等于圆的半径求得参数,有时利用后面方法计算,运算量较小.
(2)解决圆与圆的位置关系的关键是抓住它的几何特征,利用两圆圆心距与两圆半径的和、差的绝对值的大小来确定两圆的位置关系,充分利用几何图形的直观性来分析问题.
2. [2021北京昌平一中高二期中] 已知圆C的圆心在x轴上,且经过点.
(1) 求线段的垂直平分线的方程;
[答案] 设的中点为,则.
由圆的性质,得,所以所以.
所以线段的垂直平分线的方程是.
(2) 求圆的标准方程;
[答案] 设圆的标准方程为其中为半径.
由圆的性质,知圆心在直线上,所以圆心为,
所以圆的标准方程为.
[答案] 设为的中点,则线段,则圆心C到直线的距离,
故,解得,所以直线的方程为.
(3) 已知直线:与圆相交于两点,且=,求直线的方程.
题型3 圆锥曲线的定义与方程
例3
(1) [2020广东实验中学高二月考] 已知椭圆 的左、右焦点分别为过的直线交椭圆于两点,若的最大值为5,则的值为( )
A. 1 B. C. D.
C
[解析] 因为,所以椭圆的焦点在轴上,可知,
因为过的直线交椭圆于两点,所以由椭圆的定义知,,
所以,
当轴时,最小,的值最大,
此时所以解得(负值舍去),故选C.
(2) 过双曲线:的左焦点作斜率为的直线,恰好与圆相切,的右顶点为,且,则双曲线的标准方程为( )
A. B.
C. D.
B
[解析] 设,则直线的方程为,即,
因为直线恰好与圆相切,
所以圆心(0,0)到直线的距离等于半径,即
则,
解得,所以,则.所以双曲线的标准方程为.
方法归纳
(1)研究有关两点的距离的最值问题时,常用定义把曲线上的点到焦点的距离转化为到另一焦点的距离或利用定义把曲线上的点到焦点的距离转化为到准线的距离,再结合几何图形,利用几何意义去解决最值的有关问题.
(2)确定双曲线或椭圆的标准方程需要一个“定位”条件,两个“定量”条件,“定位”是指确定焦点在哪条坐标轴上,“定量”是指确定的值,常用待定系数法求得.
3. 已知椭圆的焦距为2,右顶点为,过原点与轴不重合的直线交于两点,线段的中点为,若直线经过的右焦点,则的方程为( )
A. B.
C. D.
C
[解析] 由题意知,设点,
则
因为直线经过点,所以,
因为,所以,所以,
解得所以所以椭圆的方程为.
题型4 圆锥曲线的性质
例4
(1) [2020山东实验中学高二月考] 已知双曲线的左、右焦点分别为,以线段为直径的圆与双曲线在第二象限的交点为,若直线与圆:相切,则双曲线的渐近线方程是( )
A. y= B. y= C. y= D. y=
A
[解析] 设直线与圆相切于点.如图.
因为是以圆的直径为斜边的圆的内接三角形,所以.
又因为圆与直线的切点为,所以.
又所以则
则因此有.
所以,因此渐近线的方程为.
(2) [2020四川成都高二期中] 已知椭圆的右焦点为,短轴的上端点为,直线交椭圆于两点.若,点到直线的距离不小于,则椭圆的离心率的取值范围是( )
A. (0,] B. (0,]
C. [,1) D. [,1)
A
[解析] 取椭圆的左焦点,连接,如图,根据对称性有,
故四边形为平行四边形,,则,
由点到的距离得
所以故e的取值范围是.
方法归纳
(1)圆锥曲线的性质问题的常见具体类型:①已知基本量求离心率或求离心率的取值范围;②已知圆锥曲线的方程求参数的取值范围;③已知曲线的某些性质求曲线方程或求曲线的其他性质.
(2)解圆锥曲线的性质问题时,一般要灵活地应用圆锥曲线的定义、方程及其图形.
4. 已知双曲线:的左、右焦点分别为点是右支上一点,连接与轴交于点若为坐标原点),则双曲线的渐近线方程为( )
A. B.
C. D.
C
[解析] 设易知与相似,由,
得即
又因为,所以,
所以所以双曲线的渐近线方程为.
5. 若椭圆的左、右焦点分别为,线段被抛物线的焦点分成5:3的两段,则椭圆的离心率为( )
A. B. C. D.
D
[解析] 由题意知,
抛物线的焦点为,由题意可得,解得,又由可得所以.
题型5 直线与圆锥曲线的综合问题
例5 [2021山东聊城一中期中] 已知椭圆的中心在原点,焦点在轴上,离心率为,且经过点,直线交椭圆于不同的两点.
(1) 求椭圆的方程;
[答案] 设椭圆的方程为,因为所以又因为所以故椭圆的方程为.
(2) 求的取值范围;
[答案] 将代入,消去整理得,解得,即的取值范围是(-5,5).
(3) 若直线不过点,试问直线的斜率之和是不是定值,若是定值,求出定值;若不是定值,说明理由.
[答案] 是定值.设直线的斜率分别为,
设由(2)知
则
分子,所以直线的斜率之和是定值0.
方法归纳
直线与圆锥曲线的综合问题,主要包括直线与圆锥曲线位置关系的判断问题、弦长问题、面积问题、定点与定值问题等,求解这类问题时,通常采用代数方法,将直线方程与圆锥曲线的方程联立,消去其中一个未知量,通过讨论所得方程的根的情况来确定位置关系,同时,还经常利用根与系数的关系,采取“设而不求”的办法求解弦长问题、面积问题.
6. 设抛物线:的焦点为,过且斜率为1的直线与交于两点,.
(1) 求抛物线和直线的方程;
[答案] 由题意得,直线l的方程为.
设,,联立消去可得
故.
所以,
解得,因此抛物线的方程是,直线的方程为.
(2) 设点是轴上的一点,且的面积为,求点的坐标.
[答案] 设,点到直线的距离为,则,
又,所以,
所以,解得,
故点的坐标为(5,0)或(-3,0).
1. [2020课标Ⅲ文,8,5分] 点(0,-1)到直线距离的最大值为
( )
A. 1 B. C. D. 2
B
[解析] 由可知直线过定点,
设,
当直线与垂直时,点到直线距离最大,此时.
2. [2020课标Ⅲ理,5,5分] 设为坐标原点,直线与抛物线:交于两点,若,则的焦点坐标为( )
A. B. C. (1,0) D. (2,0)
B
[解析] 因为直线与抛物线交于两点,且,
根据抛物线的对称性可以确定14,
所以(不妨设在第一象限),
代入抛物线方程得,得,所以焦点坐标为,故选B.
3. [2020课标Ⅱ理,5,5分] 若过点(2,1)的圆与两坐标轴都相切,则圆心到直线的距离为( )
A. B. C. D.
B
[解析] 因为圆上的点(2,1)在第一象限,若圆心不在第一象限,则圆至少与一条坐标轴相交,不符合题意,所以圆心必在第一象限,设圆心的坐标为,则圆的半径为,圆的标准方程为.由题意可得,可得,解得,所以圆心的坐标为(1,1)或(5,5),圆心到直线的距离.
4. [2020课标Ⅲ理,11,5分] 设双曲线:的左、右焦点分别为离心率为是上一点,且.若的面积为4,则( )
A. 1 B. 2 C. 4 D. 8
A
[解析] ,,又,即解得(负值舍去),故选A.
5. [2020新高考Ⅰ,9,5分] (多选)已知曲线:.( )
A. 若,则是椭圆,其焦点在轴上
B. 若,则是圆,其半径为
C. 若,则是双曲线,其渐近线方程为
D. 若,,则是两条直线
ACD
[解析] 对于,若,则可化为,因为,所以,即曲线表示焦点在y轴上的椭圆,故选项A正确;对于若则可化为此时曲线表示圆心在原点,半径为的圆,故选项B不正确;对于若则可化为此时曲线表示双曲线,由可得
,故选项C正确;对于D,若则可化为即,此时曲线表示平行于x轴的两条直线,故选项D正确,故选ACD.
6. [2020课标Ⅰ理,15,5分] 已知为双曲线:的右焦点,为的右顶点,为上的点,且垂直于轴.若的斜率为3,则的离心率为____.
2
[解析] 依题可得,,而即变形得,化简可得,解得或(舍去).
