3.1.2两条直线平行与垂直的判定(上)
文档属性
| 名称 | 3.1.2两条直线平行与垂直的判定(上) |  | |
| 格式 | zip | ||
| 文件大小 | 758.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-23 16:03:55 | ||
图片预览






文档简介
课件14张PPT。3.1.2 两条直线平行与垂直的判定(上)湖南省耒阳市振兴学校
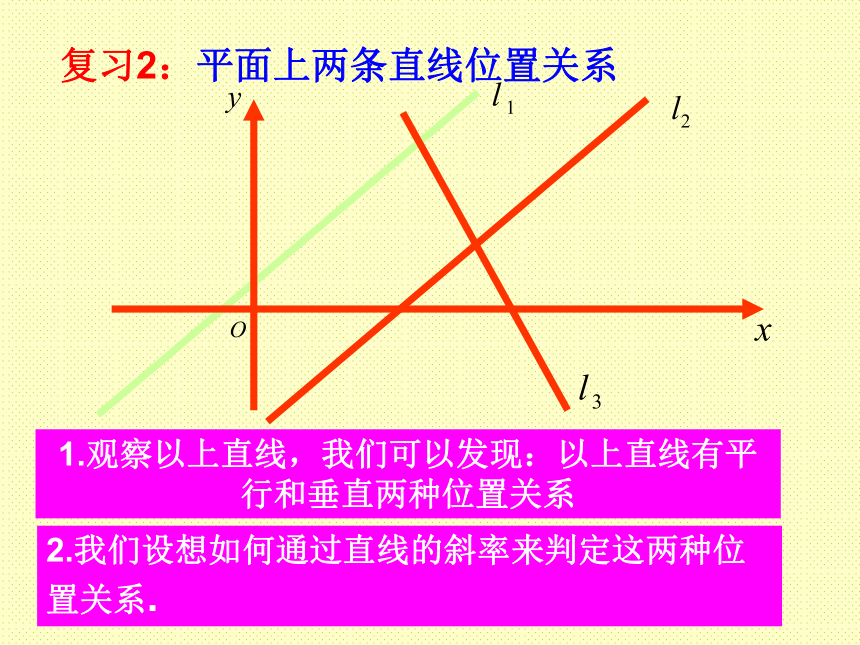
高中数学老师欧阳文丰制作复习1三要素1.观察以上直线,我们可以发现:以上直线有平行和垂直两种位置关系复习2:平面上两条直线位置关系2.我们设想如何通过直线的斜率来判定这两种位置关系. 新课引入1.斜率存在时两直线平行例如,用斜率证明三个点共线时就需要用到这个结论. 己知三点A(1,2),B(-1,0),C(3,4)这三点是否在同一条直线上,为什么?练习1:解:又因为直线AB和AC有公共点A,所以这三点在同一条直线上2.斜率不存在时两直线平行(不重合)(即:两条直线的斜率都不存在时)两直线平行2. 已知过A(-2, m)和B(m ,4)的直线与斜率为-2的直线平行,则m的值为( )
A. - 8 B. 0 C. 2 D. 10 1. 判断下列直线对是否平行
经过两点A( 2, 3), B(-1, 0)的直线
经过点P(1,0)且斜率为1的直线平行A练习2:例题讲解例3: 已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.解:例4:已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.解:ABCD(3)若两条不重合的直线的斜率都不存在,则它
们平行。
(1) 若两条直线的斜率相等,则这两条直线一定平行。 练习3: 判断题(2)若两条直线平行,则它们的斜率一定相等。(×)(×)(√)能力提升 补充例题.已知A(1,5),B(-1,1),C(3,2),若四边形ABCD是平行四边形,求D点的坐标. 2. 利用斜率研究直线位置关系必须讨论是 否存在.1. 代数方法判定两直线平行的结论: 若直线l1、l2存在斜率k1, k2,则 l1 //l2 k1=k2, (其中l1, l2不重合); l1//l2或 l1与l2重合若l1、l2可能重合,则k1=k2归纳总结:布置作业: 课本89页练习6题。
高中数学老师欧阳文丰制作复习1三要素1.观察以上直线,我们可以发现:以上直线有平行和垂直两种位置关系复习2:平面上两条直线位置关系2.我们设想如何通过直线的斜率来判定这两种位置关系. 新课引入1.斜率存在时两直线平行例如,用斜率证明三个点共线时就需要用到这个结论. 己知三点A(1,2),B(-1,0),C(3,4)这三点是否在同一条直线上,为什么?练习1:解:又因为直线AB和AC有公共点A,所以这三点在同一条直线上2.斜率不存在时两直线平行(不重合)(即:两条直线的斜率都不存在时)两直线平行2. 已知过A(-2, m)和B(m ,4)的直线与斜率为-2的直线平行,则m的值为( )
A. - 8 B. 0 C. 2 D. 10 1. 判断下列直线对是否平行
经过两点A( 2, 3), B(-1, 0)的直线
经过点P(1,0)且斜率为1的直线平行A练习2:例题讲解例3: 已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.解:例4:已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.解:ABCD(3)若两条不重合的直线的斜率都不存在,则它
们平行。
(1) 若两条直线的斜率相等,则这两条直线一定平行。 练习3: 判断题(2)若两条直线平行,则它们的斜率一定相等。(×)(×)(√)能力提升 补充例题.已知A(1,5),B(-1,1),C(3,2),若四边形ABCD是平行四边形,求D点的坐标. 2. 利用斜率研究直线位置关系必须讨论是 否存在.1. 代数方法判定两直线平行的结论: 若直线l1、l2存在斜率k1, k2,则 l1 //l2 k1=k2, (其中l1, l2不重合); l1//l2或 l1与l2重合若l1、l2可能重合,则k1=k2归纳总结:布置作业: 课本89页练习6题。
