2021-2022学年山东省淄博市桓台县八年级(上)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年山东省淄博市桓台县八年级(上)期末数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 841.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 16:41:37 | ||
图片预览



文档简介
2021-2022学年山东省淄博市桓台县八年级第一学期期末数学试卷(五四学制)
一、选择题(请把正确选项填在表格中,本大题共12个小题,每小题5分,共计60分,在每小题所给出的四个选项中,只有一项是符合题目要求的)
1.下列多项式不能用公式法进行因式分解的是( )
A.﹣a2﹣16 B. C.a2﹣10a+25 D.a2﹣64
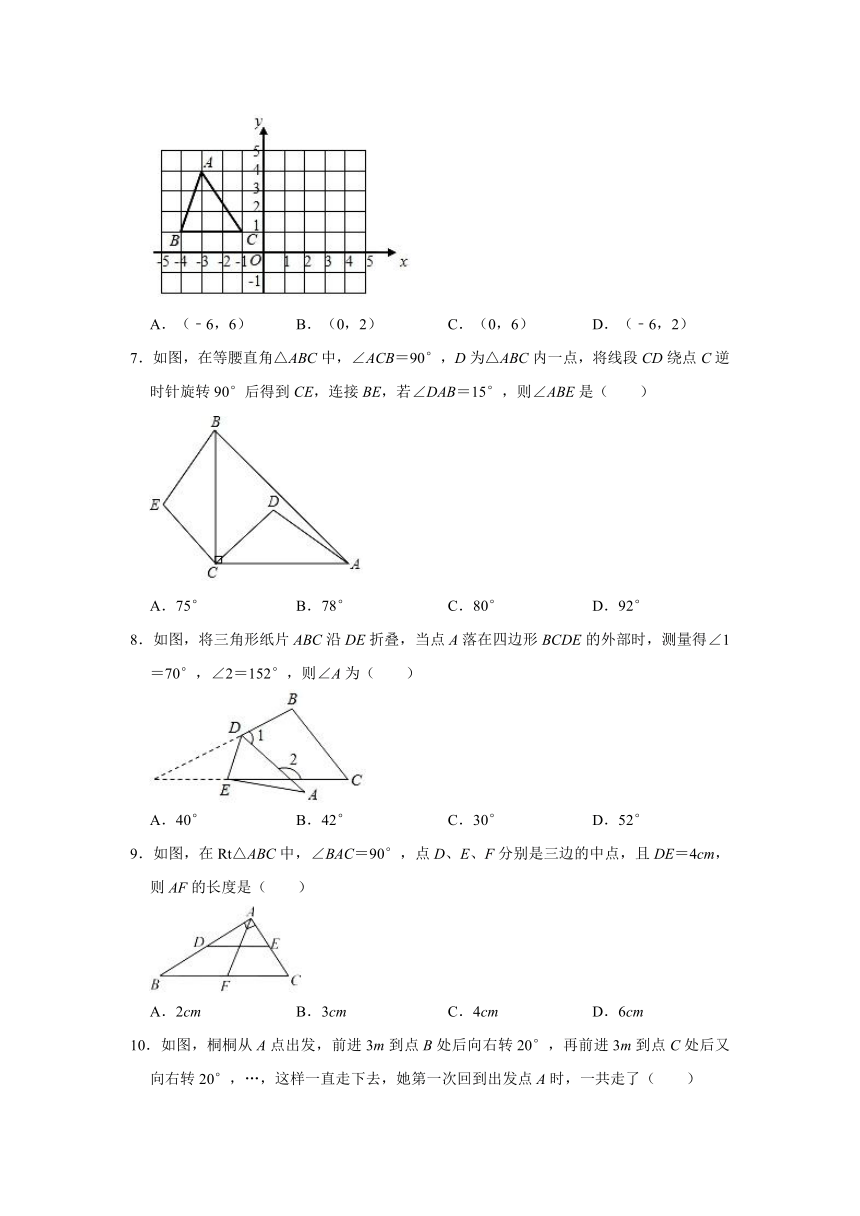
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.要使分式有意义,则x的取值应满足( )
A.x=2 B.x<2 C.x>2 D.x≠2
4.如图,在 ABCD中,若∠A=∠D+40°,则∠B的度数为( )
A.110° B.70° C.55° D.35°
5.今年收获一批成熟的果子.选取了5棵果树,采摘后分别称重,每棵果树果子总质量(单位:kg)分别为:90,100,120,110,90.这五个数据的众数和中位数分别是( )
A.90,120 B.90,110 C.90,100 D.100,100
6.△ABC的顶点分别位于正方形网格的格点上,建立如图所示的平面直角坐标系,已知点C(﹣1,1),将△ABC先沿x轴方向向右平移3个单位长度,再沿y轴方向向下平移2个单位长度,得到△A′B′C′,则点A的对应点A′的坐标是( )
A.(﹣6,6) B.(0,2) C.(0,6) D.(﹣6,2)
7.如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC内一点,将线段CD绕点C逆时针旋转90°后得到CE,连接BE,若∠DAB=15°,则∠ABE是( )
A.75° B.78° C.80° D.92°
8.如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BCDE的外部时,测量得∠1=70°,∠2=152°,则∠A为( )
A.40° B.42° C.30° D.52°
9.如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且DE=4cm,则AF的长度是( )
A.2cm B.3cm C.4cm D.6cm
10.如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
11.如图,在△ABC中,∠BAC=105°,将△ABC绕点A按顺时针方向旋转得到△AB'C'.若点B'恰好落在边BC上,且AB'=CB',则∠C'的度数为( )
A.19° B.24° C.25° D.30°
12.如图,在 ABCD中,以A为圆心,AB长为半径画弧交AD于F.分别以点F,B为圆心,大于BF长为半径作弧,两弧交于点G,作射线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.6 C.8 D.10
二、填空题(本大题共5个小题,每小题4分,共20.分。请直接填写最后结果。)
13.一组数据﹣1、2、3、4的极差是 .
14.已知,实数a满足a(a+1)=1,则a2++2021= .
15.若点A(2x﹣1,﹣5)和点B(3,y﹣3)关于原点对称,则xy的值为 .
16.如图,将Rt△ABC沿CB方向平移后,得到Rt△DEF.若AG=3,BE=6,DE=10,则阴影部分的面积为 .
17.如图,平行四边形ABCD中,对角线AC、BD相交于点O,若AB=2,BC=3,∠ABC=60°,则图中阴影部分的面积是 .
三、解答题(本大题共7个小题,共70分。解答要写出必要的文字说明、证明过程或演算步骤。)
18.绿水青山就是金山银山,为了改善生态环境,某村计划在荒坡上种树960棵.防止雨季到来,影响工期,实际每天种树的棵数是原计划的倍,结果提前4天完成任务.原计划每天种树多少棵?
19.已知 ABCD的边长如图所示,求 ABCD的周长.
20.已知,如图在 ABCD中,对角线AC和BD相交于点O,点E,F分别在OD,BO上,且OE=OF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)延长AE交CD于点G,延长CF交AB于点H.求证:AH=CG.
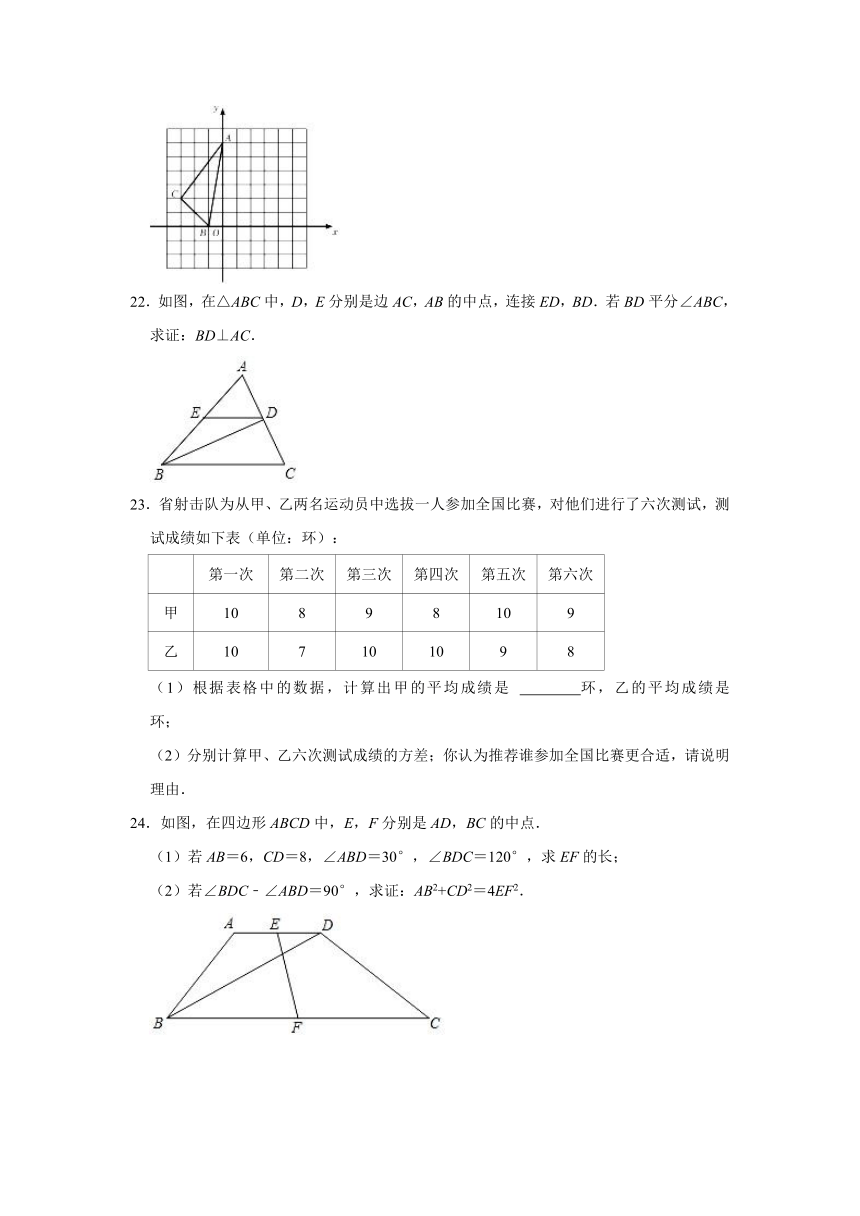
21.如图,正方形网格中,每个小正方形的边长都是单位1,△ABC的位置如图.
(1)画出将△ABC向右平移2个单位得到的△A1B1C1;
(2)画出△ABC绕点O顺时针旋转90°后得到的△A2B2C2;
(3)写出C1的坐标 ;写出C2的坐标 .
22.如图,在△ABC中,D,E分别是边AC,AB的中点,连接ED,BD.若BD平分∠ABC,求证:BD⊥AC.
23.省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 第二次 第三次 第四次 第五次 第六次
甲 10 8 9 8 10 9
乙 10 7 10 10 9 8
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;你认为推荐谁参加全国比赛更合适,请说明理由.
24.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
参考答案
一、选择题(请把正确选项填在表格中,本大题共12个小题,每小题5分,共计60分,在每小题所给出的四个选项中,只有一项是符合题目要求的)
1.下列多项式不能用公式法进行因式分解的是( )
A.﹣a2﹣16 B. C.a2﹣10a+25 D.a2﹣64
【分析】根据平方差公式和完全平方公式分解逐一判断即可.
解:A.﹣a2﹣16,不能用公式法进行因式分解,故A符合题意;
B.a2+a+=(a+)2,故B不符合题意;
C.a2﹣10a+25=(a﹣5)2,故C不符合题意;
D.a2﹣64=(a+8)(a﹣8),故D不符合题意;
故选:A.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:A.是中心对称图形,不是轴对称图形,故此选项不合题意;
B.是轴对称图形不是中心对称图形,故此选项不合题意;
C.既是轴对称图形又是中心对称图形,故此选项符合题意;
D.是轴对称图形不是中心对称图形,故此选项不合题意.
故选:C.
3.要使分式有意义,则x的取值应满足( )
A.x=2 B.x<2 C.x>2 D.x≠2
【分析】根据分式有意义的条件即可得出答案.
解:根据题意得:x﹣2≠0,
∴x≠2,
故选:D.
4.如图,在 ABCD中,若∠A=∠D+40°,则∠B的度数为( )
A.110° B.70° C.55° D.35°
【分析】由平行四边形的性质可得∠B=∠D,∠A+∠D=180°,即可求∠B的度数.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,∠B=∠D,
∴∠A+∠D=180°,
∵∠A=∠D+40°,
∴∠D=70°,
∴∠B=70°,
故选:B.
5.今年收获一批成熟的果子.选取了5棵果树,采摘后分别称重,每棵果树果子总质量(单位:kg)分别为:90,100,120,110,90.这五个数据的众数和中位数分别是( )
A.90,120 B.90,110 C.90,100 D.100,100
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数,众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
解:∵90出现了2次,出现的次数最多,
∴这五个数据的众数是90kg;
把这些数从小到大排列为:90,90,100,110,120,
则中位数是100kg;
故选:C.
6.△ABC的顶点分别位于正方形网格的格点上,建立如图所示的平面直角坐标系,已知点C(﹣1,1),将△ABC先沿x轴方向向右平移3个单位长度,再沿y轴方向向下平移2个单位长度,得到△A′B′C′,则点A的对应点A′的坐标是( )
A.(﹣6,6) B.(0,2) C.(0,6) D.(﹣6,2)
【分析】根据坐标系写出点A的坐标,根据坐标平移规律解答即可.
解:由平面直角坐标系可知,点A的坐标为(﹣3,4),
沿x轴方向向右平移3个单位长度,得到(0,4),
再沿y轴方向向下平移2个单位长度得到(0,2),
则点A的对应点A′的坐标(0,2),
故选:B.
7.如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC内一点,将线段CD绕点C逆时针旋转90°后得到CE,连接BE,若∠DAB=15°,则∠ABE是( )
A.75° B.78° C.80° D.92°
【分析】由旋转的性质可得CE=CD,∠DCE=∠ACB=90°,由“SAS”可证△ACD≌△BCE,可得∠CAD=∠CBE=30°,即可求解.
解:在等腰直角△ABC中,∠ACB=90°,
∴AC=BC,∠CBA=∠CAB=45°,
∵∠DAB=15°,
∴∠CAD=30°,
∵将线段CD绕点C逆时针旋转90°后得到CE,
∴CE=CD,∠DCE=∠ACB=90°,
∴∠BCE=∠ACD,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE=30°,
∴∠ABE=∠ABC+∠CBE=75°,
故选:A.
8.如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BCDE的外部时,测量得∠1=70°,∠2=152°,则∠A为( )
A.40° B.42° C.30° D.52°
【分析】利用四边形的内角和定理求出∠B+∠C,再利用三角形的内角和定理可得结果.
解:∵∠1=70°,∠2=152°,
∴∠B+∠C=360°﹣∠1﹣∠2=360°﹣70°﹣152°=138°,
∴∠A=180°﹣(∠B+∠C)=180°﹣138°=42°,
故选:B.
9.如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且DE=4cm,则AF的长度是( )
A.2cm B.3cm C.4cm D.6cm
【分析】根据三角形中位线定理求出BC,根据直角三角形的性质解答即可.
解:∵点D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE=8cm,
在Rt△BAC中,点F分别是斜边BC的中点,
则AF=BC=4cm,
故选:C.
10.如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
【分析】根据多边形的外角和及每一个外角的度数,可求出多边形的边数,再根据题意求出正多边形的周长即可.
解:由题意可知,当她第一次回到出发点A时,所走过的图形是一个正多边形,
由于正多边形的外角和是360°,且每一个外角为20°,
360°÷20°=18,
所以它是一个正18边形,
因此所走的路程为18×3=54(m),
故选:C.
11.如图,在△ABC中,∠BAC=105°,将△ABC绕点A按顺时针方向旋转得到△AB'C'.若点B'恰好落在边BC上,且AB'=CB',则∠C'的度数为( )
A.19° B.24° C.25° D.30°
【分析】由旋转的性质可得AB=AB',由等腰三角形的性质可得∠ABB'=∠AB'B,∠C=∠B'AC,由三角形的内角和定理可求解.
解:∵将△ABC绕点A顺时针方向旋转得到△AB′C′,
∴AB=AB',
∴∠ABB'=∠AB'B,
∵AB′=CB′,
∴∠C=∠B'AC,
∴∠AB'B=2∠C=∠ABB',
∵∠BAC=105°,
∴∠C+∠ABB'=75°,
∴∠C=25°,
故选:C.
12.如图,在 ABCD中,以A为圆心,AB长为半径画弧交AD于F.分别以点F,B为圆心,大于BF长为半径作弧,两弧交于点G,作射线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.6 C.8 D.10
【分析】设AE交BF于点O.证明四边形ABEF是菱形,利用勾股定理求出OA即可解决问题.
解:如图,设AE交BF于点O.
由作图可知:AB=AF,∠FAE=∠BAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=AF,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴OA=OE,OB=OF=3,
在Rt△AOB中,∵∠AOB=90°,
∴OA==4,
∴AE=2OA=8.
故选:C.
二、填空题(本大题共5个小题,每小题4分,共20.分。请直接填写最后结果。)
13.一组数据﹣1、2、3、4的极差是 5 .
【分析】极差是一组数中最大值与最小值的差.
解:极差为:4﹣(﹣1)=4+1=5.
故答案为:5.
14.已知,实数a满足a(a+1)=1,则a2++2021= 2022 .
【分析】由已知等式得出a+1=,代入原式有原式=a2++2021=a2+a+2021=a(a+1)+2021,再进一步代入计算即可.
解:∵a(a+1)=1,
∴a+1=,
则原式=a2++2021
=a2+a+2021
=a(a+1)+2021
=1+2021
=2022,
故答案为:2022.
15.若点A(2x﹣1,﹣5)和点B(3,y﹣3)关于原点对称,则xy的值为 1 .
【分析】直接利用关于原点对称点的性质(两个点关于原点对称时,它们的坐标符号相反)得出x,y的值,进而得出答案.
解:∵点A(2x﹣1,﹣5)和点B(3,y﹣3)关于原点对称,
∴2x﹣1+3=0,y﹣3﹣5=0,
解得:x=﹣1,y=8,
则xy=(﹣1)8=1.
故答案为:1.
16.如图,将Rt△ABC沿CB方向平移后,得到Rt△DEF.若AG=3,BE=6,DE=10,则阴影部分的面积为 51 .
【分析】根据平移的性质得到S△ABC=S△DEF,AB=DE=10,则BG=7,利用面积的和差得到S阴影部分=S梯形BEDG,然后根据梯形的面积公式计算.
解:∵Rt△ABC沿CB方向平移后,得到Rt△DEF,
∴S△ABC=S△DEF,AB=DE=10,
∴S△ABC﹣S△BGF=S△DEF﹣S△BGF,BG=AB﹣AG=10﹣3=7,
即S阴影部分=S梯形BEDG=×(7+10)×6=51.
故答案为51.
17.如图,平行四边形ABCD中,对角线AC、BD相交于点O,若AB=2,BC=3,∠ABC=60°,则图中阴影部分的面积是 .
【分析】作AM⊥BC于M,如图所示:根据直角三角形的性质得到BM=AB=×2=1,根据勾股定理得到AM===,得到S平行四边形ABCD=BC AM=3,根据平行四边形的性质得到AD∥BC,BO=DO,根据全等三角形的性质得到S△BOE=S△DOF,于是得到结论.
解:作AM⊥BC于M,如图所示:
则∠AMB=90°,
∵∠ABC=60°,
∴∠BAM=30°,
∴BM=AB=×2=1,
在Rt△ABM中,AB2=AM2+BM2,
∴AM===,
∴S平行四边形ABCD=BC AM=3,
∵四边形ABCD是平行四边形,
∴AD∥BC,BO=DO,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴S△BOE=S△DOF,
∴图中阴影部分的面积= ABCD的面积=,
故答案为:.
三、解答题(本大题共7个小题,共70分。解答要写出必要的文字说明、证明过程或演算步骤。)
18.绿水青山就是金山银山,为了改善生态环境,某村计划在荒坡上种树960棵.防止雨季到来,影响工期,实际每天种树的棵数是原计划的倍,结果提前4天完成任务.原计划每天种树多少棵?
【分析】设原计划每天种树x棵,由题意得等量关系:原计划所用天数﹣实际所用天数=4,根据等量关系,列出方程,再解即可.
解:设原计划每天种树x棵,由题意可得:
﹣=4,
解得:x=60,
经检验,x=60是原方程的解,
答:原计划每天种树60棵.
19.已知 ABCD的边长如图所示,求 ABCD的周长.
【分析】先根据平行四边形的性质建立方程求出x的值,从而求出平行四边形的边长就可以求出平行四边形的周长.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AB=,CD=,
∴,
∴x=21,
经检验x=21是原方程的解.
∴CD=,
∴AB=CD=,AD=BC=3,
∴平行四边形ABCD的周长为:(+3)×2=.
20.已知,如图在 ABCD中,对角线AC和BD相交于点O,点E,F分别在OD,BO上,且OE=OF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)延长AE交CD于点G,延长CF交AB于点H.求证:AH=CG.
【分析】(1)根据四边形ABCD是平行四边形,得AD=BC,AD∥BC,BO=DO,可证∠ADE=∠CBF,DE=BF,然后通过SAS即可证得△ADE≌△CBF;
(2)证出四边形AHCG是平行四边形,由平行四边形的性质可得出结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,BO=DO,
∴∠ADE=∠CBF,
∵OE=OF,
∴DE=BF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAC=∠BCA,
∵△ADE≌△CBF,
∴∠DAE=∠BCF,
∴∠EAO=∠FCO,
∴AG∥HC,
∵AH∥CG,
∴四边形AHCG是平行四边形,
∴AH=CG.
21.如图,正方形网格中,每个小正方形的边长都是单位1,△ABC的位置如图.
(1)画出将△ABC向右平移2个单位得到的△A1B1C1;
(2)画出△ABC绕点O顺时针旋转90°后得到的△A2B2C2;
(3)写出C1的坐标 (﹣1,2) ;写出C2的坐标 (2,3) .
【分析】(1)根据平移的性质即可画出将△ABC向右平移2个单位得到的△A1B1C1;
(2)根据旋转的性质即可画出△ABC绕点O顺时针旋转90°后得到的△A2B2C2;
(3)结合(1)和(2)即可写出C1的坐标;C2的坐标.
解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)C1的坐标(﹣1,2);C2的坐标(2,3).
故答案为:(﹣1,2);(2,3).
22.如图,在△ABC中,D,E分别是边AC,AB的中点,连接ED,BD.若BD平分∠ABC,求证:BD⊥AC.
【分析】根据三角形中位线定理得到DE∥BC,BC=2DE,根据平行线的性质、角平分线的定义得到∠EBD=∠EDB,证明DE=BE,进而得出AB=BC,根据等腰三角形的三线合一证明即可.
【解答】证明:∵D,E分别是边AC,AB的中点,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,
∵BD平分∠ABC,
∴∠CBD=∠EBD,
∵DE∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴DE=BE,
∵AB=2BE,
∴AB=2DE,
∴AB=BC,
∵点D是AC的中点,
∴BD⊥AC.
23.省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 第二次 第三次 第四次 第五次 第六次
甲 10 8 9 8 10 9
乙 10 7 10 10 9 8
(1)根据表格中的数据,计算出甲的平均成绩是 9 环,乙的平均成绩是 9 环;
(2)分别计算甲、乙六次测试成绩的方差;你认为推荐谁参加全国比赛更合适,请说明理由.
【分析】(1)根据表格中的数据可以算出甲和乙的平均环数;
(2)根据表格中的数据可以分别计算出甲和乙的方差,然后根据方差越小越稳定即可解答本题.
解:(1)甲的平均成绩是:(10+8+9+8+10+9)÷6=9(环),
乙的平均成绩是:(10+7+10+10+9+8)÷6=9(环),
故答案为:9,9;
(2)推荐甲参加全国比赛更合适,
理由:甲的方差是:×[2×(10﹣9)2+2×(8﹣9)2+2×(9﹣9)2]=,
乙的方差是:×[3×(10﹣9)2+(7﹣9)2+(8﹣9)2+(9﹣9)2]=,
∵<,
∴推荐甲参加全国比赛更合适.
24.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
【分析】(1)取BD的中点P,利用三角形中位线定理可以求得EP、FP的长度,然后利用勾股定理来求EF的长度;
(2)如图,取BD的中点P,连接EP、FP.用三角形中位线定理可以求得EP、FP的长度,然后利用勾股定理即可得到结论.
【解答】(1)解:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,AB=6,CD=8,
∴PE∥AB,且PE=AB=3,PF∥CD且PF=CD=4.
又∵∠ABD=30°,∠BDC=120°,
∴∠EPD=∠ABD=30°,∠DPF=180°﹣∠BDC=60°,
∴∠EPF=∠EPD+∠DPF=90°,
在直角△EPF中,由勾股定理得到:EF===5,
即EF=5;
(2)证明:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,
∴PE∥AB,且PE=AB,PF∥CD且PF=CD.
∴∠EPD=∠ABD,∠BPF=∠BDC,
∴∠DPF=180°﹣∠BPF=180°﹣∠BDC,
∵∠BDC﹣∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°﹣∠BDC=∠ABD+180°﹣(90°+∠ABD)=90°,
∴PE2+PF2=(AB)2+(CD)2=EF2,
∴AB2+CD2=4EF2.
一、选择题(请把正确选项填在表格中,本大题共12个小题,每小题5分,共计60分,在每小题所给出的四个选项中,只有一项是符合题目要求的)
1.下列多项式不能用公式法进行因式分解的是( )
A.﹣a2﹣16 B. C.a2﹣10a+25 D.a2﹣64
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.要使分式有意义,则x的取值应满足( )
A.x=2 B.x<2 C.x>2 D.x≠2
4.如图,在 ABCD中,若∠A=∠D+40°,则∠B的度数为( )
A.110° B.70° C.55° D.35°
5.今年收获一批成熟的果子.选取了5棵果树,采摘后分别称重,每棵果树果子总质量(单位:kg)分别为:90,100,120,110,90.这五个数据的众数和中位数分别是( )
A.90,120 B.90,110 C.90,100 D.100,100
6.△ABC的顶点分别位于正方形网格的格点上,建立如图所示的平面直角坐标系,已知点C(﹣1,1),将△ABC先沿x轴方向向右平移3个单位长度,再沿y轴方向向下平移2个单位长度,得到△A′B′C′,则点A的对应点A′的坐标是( )
A.(﹣6,6) B.(0,2) C.(0,6) D.(﹣6,2)
7.如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC内一点,将线段CD绕点C逆时针旋转90°后得到CE,连接BE,若∠DAB=15°,则∠ABE是( )
A.75° B.78° C.80° D.92°
8.如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BCDE的外部时,测量得∠1=70°,∠2=152°,则∠A为( )
A.40° B.42° C.30° D.52°
9.如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且DE=4cm,则AF的长度是( )
A.2cm B.3cm C.4cm D.6cm
10.如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
11.如图,在△ABC中,∠BAC=105°,将△ABC绕点A按顺时针方向旋转得到△AB'C'.若点B'恰好落在边BC上,且AB'=CB',则∠C'的度数为( )
A.19° B.24° C.25° D.30°
12.如图,在 ABCD中,以A为圆心,AB长为半径画弧交AD于F.分别以点F,B为圆心,大于BF长为半径作弧,两弧交于点G,作射线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.6 C.8 D.10
二、填空题(本大题共5个小题,每小题4分,共20.分。请直接填写最后结果。)
13.一组数据﹣1、2、3、4的极差是 .
14.已知,实数a满足a(a+1)=1,则a2++2021= .
15.若点A(2x﹣1,﹣5)和点B(3,y﹣3)关于原点对称,则xy的值为 .
16.如图,将Rt△ABC沿CB方向平移后,得到Rt△DEF.若AG=3,BE=6,DE=10,则阴影部分的面积为 .
17.如图,平行四边形ABCD中,对角线AC、BD相交于点O,若AB=2,BC=3,∠ABC=60°,则图中阴影部分的面积是 .
三、解答题(本大题共7个小题,共70分。解答要写出必要的文字说明、证明过程或演算步骤。)
18.绿水青山就是金山银山,为了改善生态环境,某村计划在荒坡上种树960棵.防止雨季到来,影响工期,实际每天种树的棵数是原计划的倍,结果提前4天完成任务.原计划每天种树多少棵?
19.已知 ABCD的边长如图所示,求 ABCD的周长.
20.已知,如图在 ABCD中,对角线AC和BD相交于点O,点E,F分别在OD,BO上,且OE=OF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)延长AE交CD于点G,延长CF交AB于点H.求证:AH=CG.
21.如图,正方形网格中,每个小正方形的边长都是单位1,△ABC的位置如图.
(1)画出将△ABC向右平移2个单位得到的△A1B1C1;
(2)画出△ABC绕点O顺时针旋转90°后得到的△A2B2C2;
(3)写出C1的坐标 ;写出C2的坐标 .
22.如图,在△ABC中,D,E分别是边AC,AB的中点,连接ED,BD.若BD平分∠ABC,求证:BD⊥AC.
23.省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 第二次 第三次 第四次 第五次 第六次
甲 10 8 9 8 10 9
乙 10 7 10 10 9 8
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;你认为推荐谁参加全国比赛更合适,请说明理由.
24.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
参考答案
一、选择题(请把正确选项填在表格中,本大题共12个小题,每小题5分,共计60分,在每小题所给出的四个选项中,只有一项是符合题目要求的)
1.下列多项式不能用公式法进行因式分解的是( )
A.﹣a2﹣16 B. C.a2﹣10a+25 D.a2﹣64
【分析】根据平方差公式和完全平方公式分解逐一判断即可.
解:A.﹣a2﹣16,不能用公式法进行因式分解,故A符合题意;
B.a2+a+=(a+)2,故B不符合题意;
C.a2﹣10a+25=(a﹣5)2,故C不符合题意;
D.a2﹣64=(a+8)(a﹣8),故D不符合题意;
故选:A.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:A.是中心对称图形,不是轴对称图形,故此选项不合题意;
B.是轴对称图形不是中心对称图形,故此选项不合题意;
C.既是轴对称图形又是中心对称图形,故此选项符合题意;
D.是轴对称图形不是中心对称图形,故此选项不合题意.
故选:C.
3.要使分式有意义,则x的取值应满足( )
A.x=2 B.x<2 C.x>2 D.x≠2
【分析】根据分式有意义的条件即可得出答案.
解:根据题意得:x﹣2≠0,
∴x≠2,
故选:D.
4.如图,在 ABCD中,若∠A=∠D+40°,则∠B的度数为( )
A.110° B.70° C.55° D.35°
【分析】由平行四边形的性质可得∠B=∠D,∠A+∠D=180°,即可求∠B的度数.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,∠B=∠D,
∴∠A+∠D=180°,
∵∠A=∠D+40°,
∴∠D=70°,
∴∠B=70°,
故选:B.
5.今年收获一批成熟的果子.选取了5棵果树,采摘后分别称重,每棵果树果子总质量(单位:kg)分别为:90,100,120,110,90.这五个数据的众数和中位数分别是( )
A.90,120 B.90,110 C.90,100 D.100,100
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数,众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
解:∵90出现了2次,出现的次数最多,
∴这五个数据的众数是90kg;
把这些数从小到大排列为:90,90,100,110,120,
则中位数是100kg;
故选:C.
6.△ABC的顶点分别位于正方形网格的格点上,建立如图所示的平面直角坐标系,已知点C(﹣1,1),将△ABC先沿x轴方向向右平移3个单位长度,再沿y轴方向向下平移2个单位长度,得到△A′B′C′,则点A的对应点A′的坐标是( )
A.(﹣6,6) B.(0,2) C.(0,6) D.(﹣6,2)
【分析】根据坐标系写出点A的坐标,根据坐标平移规律解答即可.
解:由平面直角坐标系可知,点A的坐标为(﹣3,4),
沿x轴方向向右平移3个单位长度,得到(0,4),
再沿y轴方向向下平移2个单位长度得到(0,2),
则点A的对应点A′的坐标(0,2),
故选:B.
7.如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC内一点,将线段CD绕点C逆时针旋转90°后得到CE,连接BE,若∠DAB=15°,则∠ABE是( )
A.75° B.78° C.80° D.92°
【分析】由旋转的性质可得CE=CD,∠DCE=∠ACB=90°,由“SAS”可证△ACD≌△BCE,可得∠CAD=∠CBE=30°,即可求解.
解:在等腰直角△ABC中,∠ACB=90°,
∴AC=BC,∠CBA=∠CAB=45°,
∵∠DAB=15°,
∴∠CAD=30°,
∵将线段CD绕点C逆时针旋转90°后得到CE,
∴CE=CD,∠DCE=∠ACB=90°,
∴∠BCE=∠ACD,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE=30°,
∴∠ABE=∠ABC+∠CBE=75°,
故选:A.
8.如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BCDE的外部时,测量得∠1=70°,∠2=152°,则∠A为( )
A.40° B.42° C.30° D.52°
【分析】利用四边形的内角和定理求出∠B+∠C,再利用三角形的内角和定理可得结果.
解:∵∠1=70°,∠2=152°,
∴∠B+∠C=360°﹣∠1﹣∠2=360°﹣70°﹣152°=138°,
∴∠A=180°﹣(∠B+∠C)=180°﹣138°=42°,
故选:B.
9.如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且DE=4cm,则AF的长度是( )
A.2cm B.3cm C.4cm D.6cm
【分析】根据三角形中位线定理求出BC,根据直角三角形的性质解答即可.
解:∵点D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE=8cm,
在Rt△BAC中,点F分别是斜边BC的中点,
则AF=BC=4cm,
故选:C.
10.如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
【分析】根据多边形的外角和及每一个外角的度数,可求出多边形的边数,再根据题意求出正多边形的周长即可.
解:由题意可知,当她第一次回到出发点A时,所走过的图形是一个正多边形,
由于正多边形的外角和是360°,且每一个外角为20°,
360°÷20°=18,
所以它是一个正18边形,
因此所走的路程为18×3=54(m),
故选:C.
11.如图,在△ABC中,∠BAC=105°,将△ABC绕点A按顺时针方向旋转得到△AB'C'.若点B'恰好落在边BC上,且AB'=CB',则∠C'的度数为( )
A.19° B.24° C.25° D.30°
【分析】由旋转的性质可得AB=AB',由等腰三角形的性质可得∠ABB'=∠AB'B,∠C=∠B'AC,由三角形的内角和定理可求解.
解:∵将△ABC绕点A顺时针方向旋转得到△AB′C′,
∴AB=AB',
∴∠ABB'=∠AB'B,
∵AB′=CB′,
∴∠C=∠B'AC,
∴∠AB'B=2∠C=∠ABB',
∵∠BAC=105°,
∴∠C+∠ABB'=75°,
∴∠C=25°,
故选:C.
12.如图,在 ABCD中,以A为圆心,AB长为半径画弧交AD于F.分别以点F,B为圆心,大于BF长为半径作弧,两弧交于点G,作射线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.6 C.8 D.10
【分析】设AE交BF于点O.证明四边形ABEF是菱形,利用勾股定理求出OA即可解决问题.
解:如图,设AE交BF于点O.
由作图可知:AB=AF,∠FAE=∠BAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=AF,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴OA=OE,OB=OF=3,
在Rt△AOB中,∵∠AOB=90°,
∴OA==4,
∴AE=2OA=8.
故选:C.
二、填空题(本大题共5个小题,每小题4分,共20.分。请直接填写最后结果。)
13.一组数据﹣1、2、3、4的极差是 5 .
【分析】极差是一组数中最大值与最小值的差.
解:极差为:4﹣(﹣1)=4+1=5.
故答案为:5.
14.已知,实数a满足a(a+1)=1,则a2++2021= 2022 .
【分析】由已知等式得出a+1=,代入原式有原式=a2++2021=a2+a+2021=a(a+1)+2021,再进一步代入计算即可.
解:∵a(a+1)=1,
∴a+1=,
则原式=a2++2021
=a2+a+2021
=a(a+1)+2021
=1+2021
=2022,
故答案为:2022.
15.若点A(2x﹣1,﹣5)和点B(3,y﹣3)关于原点对称,则xy的值为 1 .
【分析】直接利用关于原点对称点的性质(两个点关于原点对称时,它们的坐标符号相反)得出x,y的值,进而得出答案.
解:∵点A(2x﹣1,﹣5)和点B(3,y﹣3)关于原点对称,
∴2x﹣1+3=0,y﹣3﹣5=0,
解得:x=﹣1,y=8,
则xy=(﹣1)8=1.
故答案为:1.
16.如图,将Rt△ABC沿CB方向平移后,得到Rt△DEF.若AG=3,BE=6,DE=10,则阴影部分的面积为 51 .
【分析】根据平移的性质得到S△ABC=S△DEF,AB=DE=10,则BG=7,利用面积的和差得到S阴影部分=S梯形BEDG,然后根据梯形的面积公式计算.
解:∵Rt△ABC沿CB方向平移后,得到Rt△DEF,
∴S△ABC=S△DEF,AB=DE=10,
∴S△ABC﹣S△BGF=S△DEF﹣S△BGF,BG=AB﹣AG=10﹣3=7,
即S阴影部分=S梯形BEDG=×(7+10)×6=51.
故答案为51.
17.如图,平行四边形ABCD中,对角线AC、BD相交于点O,若AB=2,BC=3,∠ABC=60°,则图中阴影部分的面积是 .
【分析】作AM⊥BC于M,如图所示:根据直角三角形的性质得到BM=AB=×2=1,根据勾股定理得到AM===,得到S平行四边形ABCD=BC AM=3,根据平行四边形的性质得到AD∥BC,BO=DO,根据全等三角形的性质得到S△BOE=S△DOF,于是得到结论.
解:作AM⊥BC于M,如图所示:
则∠AMB=90°,
∵∠ABC=60°,
∴∠BAM=30°,
∴BM=AB=×2=1,
在Rt△ABM中,AB2=AM2+BM2,
∴AM===,
∴S平行四边形ABCD=BC AM=3,
∵四边形ABCD是平行四边形,
∴AD∥BC,BO=DO,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴S△BOE=S△DOF,
∴图中阴影部分的面积= ABCD的面积=,
故答案为:.
三、解答题(本大题共7个小题,共70分。解答要写出必要的文字说明、证明过程或演算步骤。)
18.绿水青山就是金山银山,为了改善生态环境,某村计划在荒坡上种树960棵.防止雨季到来,影响工期,实际每天种树的棵数是原计划的倍,结果提前4天完成任务.原计划每天种树多少棵?
【分析】设原计划每天种树x棵,由题意得等量关系:原计划所用天数﹣实际所用天数=4,根据等量关系,列出方程,再解即可.
解:设原计划每天种树x棵,由题意可得:
﹣=4,
解得:x=60,
经检验,x=60是原方程的解,
答:原计划每天种树60棵.
19.已知 ABCD的边长如图所示,求 ABCD的周长.
【分析】先根据平行四边形的性质建立方程求出x的值,从而求出平行四边形的边长就可以求出平行四边形的周长.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AB=,CD=,
∴,
∴x=21,
经检验x=21是原方程的解.
∴CD=,
∴AB=CD=,AD=BC=3,
∴平行四边形ABCD的周长为:(+3)×2=.
20.已知,如图在 ABCD中,对角线AC和BD相交于点O,点E,F分别在OD,BO上,且OE=OF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)延长AE交CD于点G,延长CF交AB于点H.求证:AH=CG.
【分析】(1)根据四边形ABCD是平行四边形,得AD=BC,AD∥BC,BO=DO,可证∠ADE=∠CBF,DE=BF,然后通过SAS即可证得△ADE≌△CBF;
(2)证出四边形AHCG是平行四边形,由平行四边形的性质可得出结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,BO=DO,
∴∠ADE=∠CBF,
∵OE=OF,
∴DE=BF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAC=∠BCA,
∵△ADE≌△CBF,
∴∠DAE=∠BCF,
∴∠EAO=∠FCO,
∴AG∥HC,
∵AH∥CG,
∴四边形AHCG是平行四边形,
∴AH=CG.
21.如图,正方形网格中,每个小正方形的边长都是单位1,△ABC的位置如图.
(1)画出将△ABC向右平移2个单位得到的△A1B1C1;
(2)画出△ABC绕点O顺时针旋转90°后得到的△A2B2C2;
(3)写出C1的坐标 (﹣1,2) ;写出C2的坐标 (2,3) .
【分析】(1)根据平移的性质即可画出将△ABC向右平移2个单位得到的△A1B1C1;
(2)根据旋转的性质即可画出△ABC绕点O顺时针旋转90°后得到的△A2B2C2;
(3)结合(1)和(2)即可写出C1的坐标;C2的坐标.
解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)C1的坐标(﹣1,2);C2的坐标(2,3).
故答案为:(﹣1,2);(2,3).
22.如图,在△ABC中,D,E分别是边AC,AB的中点,连接ED,BD.若BD平分∠ABC,求证:BD⊥AC.
【分析】根据三角形中位线定理得到DE∥BC,BC=2DE,根据平行线的性质、角平分线的定义得到∠EBD=∠EDB,证明DE=BE,进而得出AB=BC,根据等腰三角形的三线合一证明即可.
【解答】证明:∵D,E分别是边AC,AB的中点,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,
∵BD平分∠ABC,
∴∠CBD=∠EBD,
∵DE∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴DE=BE,
∵AB=2BE,
∴AB=2DE,
∴AB=BC,
∵点D是AC的中点,
∴BD⊥AC.
23.省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 第二次 第三次 第四次 第五次 第六次
甲 10 8 9 8 10 9
乙 10 7 10 10 9 8
(1)根据表格中的数据,计算出甲的平均成绩是 9 环,乙的平均成绩是 9 环;
(2)分别计算甲、乙六次测试成绩的方差;你认为推荐谁参加全国比赛更合适,请说明理由.
【分析】(1)根据表格中的数据可以算出甲和乙的平均环数;
(2)根据表格中的数据可以分别计算出甲和乙的方差,然后根据方差越小越稳定即可解答本题.
解:(1)甲的平均成绩是:(10+8+9+8+10+9)÷6=9(环),
乙的平均成绩是:(10+7+10+10+9+8)÷6=9(环),
故答案为:9,9;
(2)推荐甲参加全国比赛更合适,
理由:甲的方差是:×[2×(10﹣9)2+2×(8﹣9)2+2×(9﹣9)2]=,
乙的方差是:×[3×(10﹣9)2+(7﹣9)2+(8﹣9)2+(9﹣9)2]=,
∵<,
∴推荐甲参加全国比赛更合适.
24.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
【分析】(1)取BD的中点P,利用三角形中位线定理可以求得EP、FP的长度,然后利用勾股定理来求EF的长度;
(2)如图,取BD的中点P,连接EP、FP.用三角形中位线定理可以求得EP、FP的长度,然后利用勾股定理即可得到结论.
【解答】(1)解:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,AB=6,CD=8,
∴PE∥AB,且PE=AB=3,PF∥CD且PF=CD=4.
又∵∠ABD=30°,∠BDC=120°,
∴∠EPD=∠ABD=30°,∠DPF=180°﹣∠BDC=60°,
∴∠EPF=∠EPD+∠DPF=90°,
在直角△EPF中,由勾股定理得到:EF===5,
即EF=5;
(2)证明:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,
∴PE∥AB,且PE=AB,PF∥CD且PF=CD.
∴∠EPD=∠ABD,∠BPF=∠BDC,
∴∠DPF=180°﹣∠BPF=180°﹣∠BDC,
∵∠BDC﹣∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°﹣∠BDC=∠ABD+180°﹣(90°+∠ABD)=90°,
∴PE2+PF2=(AB)2+(CD)2=EF2,
∴AB2+CD2=4EF2.
同课章节目录
