2021-2022学年山东省潍坊市诸城市九年级(上)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年山东省潍坊市诸城市九年级(上)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 16:58:51 | ||
图片预览




文档简介
2021-2022学年山东省潍坊市诸城市九年级第一学期期末数学试卷
一、选择题(本题共8小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,多选、不选、错选均记0分.)
1.方程(x﹣1)x=2x的解是( )
A.x=3 B.x1=0,x2=3 C.x1=0,x2=1 D.x1=1,x2=3
2.某人沿着斜坡前进,当他前进30米时上升的高度为15米,则斜坡的坡度i等于( )
A.1:2 B.1: C.1: D.2:1
3.如图,⊙O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为( )
A.70° B.110° C.120° D.130°
4.如图,∠ABC=30°,边BA上有一点D,DB=6,以点D为圆心,以DB长为半径作弧交BC于点E,则BE的长是( )
A. B.6 C. D.12
5.若点A(x1,﹣3),B(x2,﹣1),C(x3,3)都在反比例函数y=(k>0)的图象上,则x1,x2,x3的大小关系是( )
A.x3>x1>x2 B.x1>x2>x3 C.x2>x1>x3 D.x1>x3>x2
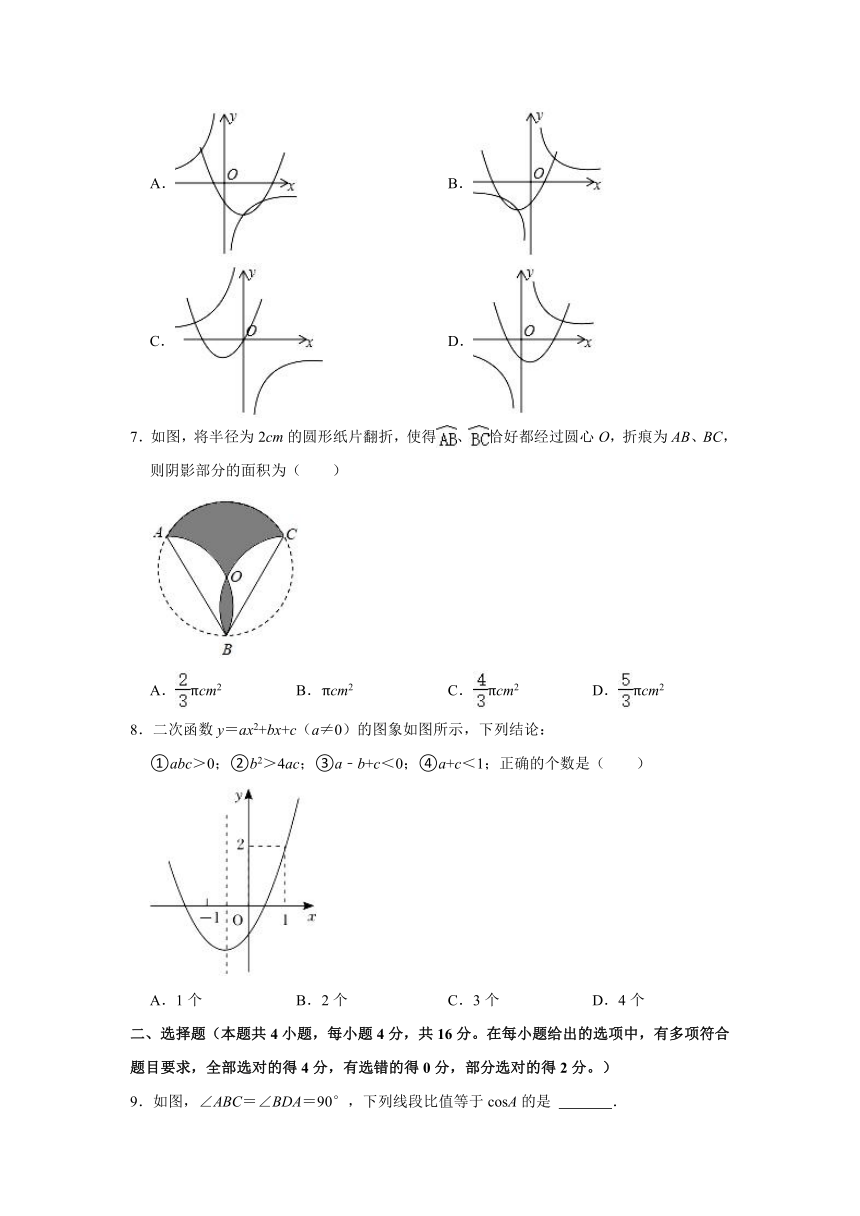
6.在同一平面直角坐标系中,反比例函数y=(k≠0)与二次函数y=x2﹣kx﹣k的大致图象是( )
A. B.
C. D.
7.如图,将半径为2cm的圆形纸片翻折,使得、恰好都经过圆心O,折痕为AB、BC,则阴影部分的面积为( )
A.πcm2 B.πcm2 C.πcm2 D.πcm2
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①abc>0;②b2>4ac;③a﹣b+c<0;④a+c<1;正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、选择题(本题共4小题,每小题4分,共16分。在每小题给出的选项中,有多项符合题目要求,全部选对的得4分,有选错的得0分,部分选对的得2分。)
9.如图,∠ABC=∠BDA=90°,下列线段比值等于cosA的是 .
A.
B.
C.
D.
10.小明同学统计了某学校九年级部分同学每天阅读图书的时间,并绘制了统计图,如图所示,下面四个推断中正确的是 .
A.小明此次一共调查了100位同学
B.每天阅读图书时间在15~30分钟的人数最多
C.每天阅读图书时间不足15分钟的同学人数多于45~60分钟的人数
D.每天阅读图书时间超过30分钟的同学人数是调查总人数的20%
11.如图,PA、PB是⊙O的切线,切点分别为A、B,BC是⊙O的直径,PO交⊙O于E点,连接AB交PO于F,连接CE交AB于D点.下列结论正确的是 .
A.CE平分∠ACB
B.△CDA≌△EDF
C.E是△PAB的内心
D.OF=AC
12.对于实数a,b,定义运算“※”:a※b=,例如:4※2,因为4>2,所以4※2=42﹣4×2=8.若函数y=(2x)※(x+1),则下列结论正确的是 .
A.方程(2x)※(x+1)=0的解为x1=﹣1,x2=1
B.当x>1时,y随x的增大而增大
C.若关于x的方程(2x)※(x+1)=m有三个解,则0<m≤1
D.当x<1时,函数y=(2x)※(x+1)的最大值为1
三、填空题(本题共4小题,共16分,只要求填写最后结果,每小题填对得4分。)
13.如图,点A在反比例函数的图象上,直角△OAB的面积为2,则k= .
14.如图,四边形ABCD内接于⊙O,延长BC到E且∠DCE=66°,则∠BOD的度数是 .
15.如图,AB为订书机的托板,压柄BC绕着点B旋转,连接DE的一端点D固定,点E从A向B处滑动,在滑动的过程中,DE的长度保持不变.在图1中,BD=6cm,BE=15cm,∠B=60°,现将压柄BC从图1旋转到与底座AB垂直,如图2所示,则此过程中点E滑动的距离为 cm.
16.某桥梁的桥洞可视为抛物线,AB=12m,最高点C距离水面4m.以AB所在直线为x轴(向右为正向),若以A为原点建立坐标系时,该抛物线的表达式为y=﹣x2+x.已知点D为抛物线上一点,位于点C右侧且距离水面3m,若以点D为原点,以平行于AB的直线为x轴(向右为正向)建立坐标系时,该抛物线的表达式为 .
四、解答题(本题共7小题,共64分。解答应写出文字说明、证明过程或演算步栗)
17.已知关于x的方程x2﹣2kx﹣=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣2,求另一个根及k值.
18.北京冬奥会将在2022年2月4日至20日举行,北京将成为奥运史上第一个举办过夏季奥运会和冬季奥运会的城市.小亮是个集邮爱好者,他收集了如图所示的5张纪念邮票(除正面内容不同外,其余均相同),现将5张邮票背面朝上,洗匀放好.
(1)小亮从中随机抽取一张邮票是“吉祥物雪容融”的概率是 ;
(2)小明发明了一种“邮票棋”比胜负的游戏,用小亮的三种邮票当作5颗棋子,其中冬奥会会徽邮票记作A棋,吉祥物冰敦敦邮票记作B棋,吉祥物雪容融邮票记作C棋.
游戏规则:将5颗棋子放入一个不透明的袋子中,然后随机从5颗棋子中摸出1颗棋子,不放回,再摸出第2颗棋子.若摸到A棋,则小明胜;若摸到两颗相同的棋子,则小亮胜;其余情况视为平局,游戏重新进行,请你用列表或画树状图的方法验证这个游戏公平吗?请说明理由.
19.如图,在四边形ABCD中,∠B=∠DCB=90°,AB=6,CD=2,△ABP与△PCD全等.
(1)求AD的长;
(2)求tan∠DAC的值.
20.如图所示,直线y=x与反比例函数y=(k≠0,x>0)的图象交于点Q(4,a),点P(m,n)是反比例函数图象上一点,且n=2m.
(1)求反比例函数和直线PQ的解析式;
(2)若点M在x轴上,使得△PMQ的面积为3,求点M的坐标.
21.某水果店以进价为每千克18元购进草莓,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克,设销售单价为x元,每天的销售量为y千克,每天获利为w元.
(1)求y与x之间的函数表达式;
(2)求w与x之间的函数表达式,并求该草莓售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果商家规定这种草莓每天的销售量不低于40千克,求每天销售利润的最大值是多少元?
22.如图,A、B、C分别是⊙O上的点,∠B=60°,CD是⊙O的直径,CD=2,E是CD延长线上的一点,且AE=AC.
(1)求证:AE是⊙O的切线;
(2)求ED的长.
23.如图,抛物线y=ax2﹣bx﹣与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C,直线AD交y轴于点E(0,1),与抛物线交于点D,点P是直线AD下方抛物线上一点(不与A,D重合).
(1)求抛物线的表达式与直线AD的表达式;
(2)过点P作PM∥y轴交直线AD于点M.当PM最大时,求出点P的坐标,PM的最大值为多少?
(3)若四边形APBM为菱形,直接写出点M的坐标.
参考答案
一、选择题(本题共8小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,多选、不选、错选均记0分.)
1.方程(x﹣1)x=2x的解是( )
A.x=3 B.x1=0,x2=3 C.x1=0,x2=1 D.x1=1,x2=3
【分析】整理后把方程的左边分解因式,即可得出两个一元一次方程,再求出方程的解即可.
解:(x﹣1)x=2x,
整理得:x2﹣3x=0,
x(x﹣3)=0,
x=0或x﹣3=0,
解得:x1=0,x2=3,
故选:B.
2.某人沿着斜坡前进,当他前进30米时上升的高度为15米,则斜坡的坡度i等于( )
A.1:2 B.1: C.1: D.2:1
【分析】由某人在斜坡上走了30米,上升的高度为15米,则可先求出某人走的水平距离,再求出这个斜坡的坡度.
解:由题意得:某人在斜坡上走了30米,上升的高度为15米,
则某人走的水平距离s==15(米),
∴坡度i=15:15=1:.
故选:C.
3.如图,⊙O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为( )
A.70° B.110° C.120° D.130°
【分析】先根据三角形的内角和定理求得∠B,再由切线的性质得∠BDO=∠BEO=90°,从而得出∠DOE.
解:∵∠BAC=50°,∠ACB=60°,
∴∠B=180°﹣50°﹣60°=70°,
∵E,D是切点,
∴∠BDO=∠BEO=90°,
∴∠DOE=180°﹣∠B,
∴∠DOE=∠A+∠C=50°+60°=110°.
故选:B.
4.如图,∠ABC=30°,边BA上有一点D,DB=6,以点D为圆心,以DB长为半径作弧交BC于点E,则BE的长是( )
A. B.6 C. D.12
【分析】过点D作DF⊥BC于F,则BE=2BF,∠BFD=90°,再利用含30度角的直角三角形的性质求出DF,进而求出BF,即可求出答案.
解:过点D作DF⊥BC于F,则BE=2BF,∠BFD=90°,
在Rt△BFD中,∠ABC=30°,BD=6,
∴DF=BD=3,
∴BF=DF=3,
∴BE=2BF=6,
故选:C.
5.若点A(x1,﹣3),B(x2,﹣1),C(x3,3)都在反比例函数y=(k>0)的图象上,则x1,x2,x3的大小关系是( )
A.x3>x1>x2 B.x1>x2>x3 C.x2>x1>x3 D.x1>x3>x2
【分析】先根据反比例函数的解析式判断出函数图象所在的象限,再根据根据反比例函数的性质,可以判断出x1,x2,x3的大小关系,本题得以解决.
解:∵反比例函数y=中k>0,
∴函数图象的两个分支分别位于一、三象限,且在每一象限内,y随x的增大而减小.
∵点A(x1,﹣3),B(x2,﹣1),C(x3,3)都在反比例函数y=(k>0)的图象上,﹣3<﹣1<0<3,
∴x2<x1<x3,
故选:A.
6.在同一平面直角坐标系中,反比例函数y=(k≠0)与二次函数y=x2﹣kx﹣k的大致图象是( )
A. B.
C. D.
【分析】根据k的取值范围分当k>0时和当k<0时两种情况进行讨论,根据反比例函数图象与性质,二次函数图象和性质进行判断即可.
解:当k>0时,反比例函数y=(k≠0)的图象经过第一、三象限,二次函数y=x2﹣kx﹣k图象的对称轴x=在y轴右侧,并与y'轴交于负半轴,则B选项不符合题意,D选项符合题意;
当k<0时,反比例函数y=(k≠0)的图象经过第二、四象限,二次函数y=x2+kx﹣k图象的对称轴x=在y轴左侧,并与y'轴交于正半轴,则A、C选项都不符合题意;
故选:D.
7.如图,将半径为2cm的圆形纸片翻折,使得、恰好都经过圆心O,折痕为AB、BC,则阴影部分的面积为( )
A.πcm2 B.πcm2 C.πcm2 D.πcm2
【分析】作OD⊥AB于点D,连接AO,BO,CO,求出∠OAD=30°,得到∠AOB=2∠AOD=120°,进而求得∠AOC=120°,再利用阴影部分的面积=S扇形AOC得出阴影部分的面积是⊙O面积的,即可得出结果.
解:作OD⊥AB于点D,连接AO,BO,CO,如图所示:
∵OD=AO
∴∠OAD=30°,
∴∠AOB=2∠AOD=120°,
同理∠BOC=120°,
∴∠AOC=120°,
∴阴影部分的面积=S扇形BOC=×⊙O面积=×π×22=π(cm2);
故选:C.
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①abc>0;②b2>4ac;③a﹣b+c<0;④a+c<1;正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】①由开口向上得到a>0,由对称轴在y轴左侧得到b>0,由函数图象与y轴的交点在y轴负半轴上得到c<0,然后得到abc<0;
②由函数图象与x轴的交点个数得到b2﹣4ac>0;
③由图象可知,当x=﹣1时,y=a﹣b+c<0;
④由图象可知,当x=1时,y=2,得到a+b+c=2,然后得到b与a、c之间的关系,再代入a﹣b+c<0得到结果.
解:①∵开口向上,对称轴在y轴左侧,函数图象与y轴的交点在y轴负半轴上,
∴a>0,b>0,c<0,
∴abc<0,故①错误,不符合题意;
②由图可知,函数图象与x轴由2个交点,
∴b2﹣4ac>0,
∴b2>4ac,故②正确,符合题意;
③由图象可知,当x=﹣1时,y<0,
∴a﹣b+c<0,故③正确,符合题意;
④由图象可知,当x=1时,y=2,
∴a+b+c=2,
∴b=2﹣a﹣c,
∵a﹣b+c<0,
∴a﹣(2﹣a﹣c)+c<0,
∴a+c<1,故④正确,符合题意,
∴正确的个数有3个,
故选:C.
二、选择题(本题共4小题,每小题4分,共16分。在每小题给出的选项中,有多项符合题目要求,全部选对的得4分,有选错的得0分,部分选对的得2分。)
9.如图,∠ABC=∠BDA=90°,下列线段比值等于cosA的是 C、D .
A.
B.
C.
D.
【分析】根据余弦等于邻边比斜边,可得答案.
解:A、在Rt△ABD中,cosA=,故本选项错误,不符合题意;
B、在Rt△ABC中,cosA=,故本选项错误,不符合题意;
C、在Rt△BCD中,cosA=cos∠DBC=,故本选项正确,符合题意;
D、在Rt△ABC中,cosA=,故本选项正确,符合题意;
故选:C、D.
10.小明同学统计了某学校九年级部分同学每天阅读图书的时间,并绘制了统计图,如图所示,下面四个推断中正确的是 A、B .
A.小明此次一共调查了100位同学
B.每天阅读图书时间在15~30分钟的人数最多
C.每天阅读图书时间不足15分钟的同学人数多于45~60分钟的人数
D.每天阅读图书时间超过30分钟的同学人数是调查总人数的20%
【分析】根据频数分布直方图的意义,逐项进行判断即可.
解:10+60+20+10=100(人),因此选项A是正确的;
每天阅读图书时间在15~30分钟的人数为60人,是几个时间段人数最多的,因此选项B是正确的;
每天阅读图书时间不足15分钟的同学人数与阅读时间在45~60分钟的人数相等,都是10人,因此选项C不正确;
每天阅读图书时间超过30分钟的同学人数是调查总人数的=30%,因此选项D不正确;
故答案为:A、B.
11.如图,PA、PB是⊙O的切线,切点分别为A、B,BC是⊙O的直径,PO交⊙O于E点,连接AB交PO于F,连接CE交AB于D点.下列结论正确的是 A,C,D .
A.CE平分∠ACB
B.△CDA≌△EDF
C.E是△PAB的内心
D.OF=AC
【分析】连接OA,BE,根据PA、PB是⊙O的切线,可得PA=PB,OA=OB,可得OP是AB的垂直平分线,根据垂径定理,进而可以判断A;根据OB=OC,AF=BF,可得OF是三角形BAC的中位线,进而即可判断D;证明∠PBE=∠EBA,∠APE=∠BPE,即可判断C;根据AC∥OE,可得△CDA∽△EDF,进而可以判断B.
解:如图,连接OA,BE,
∵PA、PB是⊙O的切线,
∴PA=PB,
∵OA=OB,
∴OP是AB的垂直平分线,
∴OP⊥AB,
∴=,
∴∠ACE=∠BCE,
∴CE平分∠ACB;故A正确;
∵BC是⊙O的直径,
∴∠BAC=90°,
∵∠BFO=90°,
∴OF∥AC,
∵OB=OC,AF=BF,
∴OF=AC;故D正确;
∵PB是⊙O的切线,
∴∠PBE+∠EBC=90°,
∵BC是⊙O的直径,
∴∠EBC+∠ECB=90°,
∴∠PBE=∠ECB,
∵∠ECB=∠EBA,
∴∠PBE=∠EBA,
∵∠APE=∠BPE,
∴E是△PAB的内心;故C正确;
∵AC∥OE,
∴△CDA∽△EDF.故B错误;
∴结论正确的是A,C,D.
故答案为:A,C,D.
12.对于实数a,b,定义运算“※”:a※b=,例如:4※2,因为4>2,所以4※2=42﹣4×2=8.若函数y=(2x)※(x+1),则下列结论正确的是 ABD .
A.方程(2x)※(x+1)=0的解为x1=﹣1,x2=1
B.当x>1时,y随x的增大而增大
C.若关于x的方程(2x)※(x+1)=m有三个解,则0<m≤1
D.当x<1时,函数y=(2x)※(x+1)的最大值为1
【分析】根据题干定义求出y=(2x)※(x+1)的解析式,根据2x≥x+1及2x<x+1可得x≥1时y=2x2﹣2x,x<1时,y=﹣x2+1,进而求解.
解:根据题意得:当2x≥x+1,即x≥1时,y=(2x)2﹣2x(x+1)=2x2﹣2x,
当2x<x+1,即x<1时,y=(x+1)2﹣2x(x+1)=﹣x2+1,
∴当x≥1时,2x2﹣2x=0,
解得x=0(舍去)或x=1,
当x<1时,﹣x2+1=0,
解得x=1(舍去)或x=﹣1,
∴(2x)※(x+1)=0的解是x1=﹣1,x2=1;
故A正确,
B、当x>1时,y=2x2﹣2x,
抛物线开口向上,对称轴是直线x=,
∴x>1时,y随x的增大而增大,
∴B选项正确.
当x≥1时,y=2x2﹣2x=2(x﹣)2﹣,
∴x=1时,y取最小值为y=0,
当x<1时,y=﹣x2+1=0,
当x=0时,y取最大值为y=1,
如图,
当0<m<1时,方程(2x)※(x+1)=m有三个解,
∴选项C错误,选项D正确.
故答案为:ABD.
三、填空题(本题共4小题,共16分,只要求填写最后结果,每小题填对得4分。)
13.如图,点A在反比例函数的图象上,直角△OAB的面积为2,则k= ﹣4 .
【分析】设A点坐标为(a,b),由于点A在反比例函数图象上,则k=ab,然后利用三角形面积公式得到×(﹣a)×b=2,则ab=﹣4,即可得到k=﹣4.
解:设A点坐标为(a,b),则k=ab,
∵S△OAB=AB OB,
∴×(﹣a)×b=2,
∴ab=﹣4,
∴k=﹣4.
故答案为﹣4.
14.如图,四边形ABCD内接于⊙O,延长BC到E且∠DCE=66°,则∠BOD的度数是 132° .
【分析】根据圆内接四边形的性质可直接得出结论.
解:∵四边形ABCD是圆内接四边形,∠DCE=66°,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠A=∠DCE=66°,
∴∠BOD=2∠A=132°.
故答案为:132°.
15.如图,AB为订书机的托板,压柄BC绕着点B旋转,连接DE的一端点D固定,点E从A向B处滑动,在滑动的过程中,DE的长度保持不变.在图1中,BD=6cm,BE=15cm,∠B=60°,现将压柄BC从图1旋转到与底座AB垂直,如图2所示,则此过程中点E滑动的距离为 (15﹣3) cm.
【分析】如图1,由直角三角形的性质和勾股定理可求DE的长,如图2,由勾股定理可求BE的长,即可求解.
解:如图1,过点D作DH⊥AB于H,
∵∠ABC=60°,
∴∠BDH=30°,
∴DH=BD=3(cm),DH=BH=3(cm),
∴EH=15﹣3=12(cm),
∴DE===3(cm),
如图2,∵∠DBE=90°,
∴BE===3(cm),
∴点E滑动的距离=(15﹣3)cm,
故答案为:(15﹣3).
16.某桥梁的桥洞可视为抛物线,AB=12m,最高点C距离水面4m.以AB所在直线为x轴(向右为正向),若以A为原点建立坐标系时,该抛物线的表达式为y=﹣x2+x.已知点D为抛物线上一点,位于点C右侧且距离水面3m,若以点D为原点,以平行于AB的直线为x轴(向右为正向)建立坐标系时,该抛物线的表达式为 y=﹣x2﹣x .
【分析】在y=﹣x2+x中,令y=3可得xD﹣xA=9,以点D为原点,以平行于AB的直线为x轴(向右为正向)建立坐标系,根据题意知此时顶点D(﹣3,1),A(﹣9,﹣3),设抛物线的表达式为y=a(x+3)2+1,将A(﹣9,﹣3)代入即得抛物线的表达式为y=﹣(x+3)2+1=﹣x2﹣x.
解:在y=﹣x2+x中,令y=3得﹣x2+x=3,
解得x=3或x=9,
∵点D为抛物线上一点,位于点C右侧且距离水面3m,
∴xD﹣xA=9,
以点D为原点,以平行于AB的直线为x轴(向右为正向)建立坐标系,如图:
根据题意知此时顶点D(﹣3,1),A(﹣9,﹣3),
设抛物线的表达式为y=a(x+3)2+1,
将A(﹣9,﹣3)代入得:36a+1=﹣3,
解得a=﹣,
∴抛物线的表达式为y=﹣(x+3)2+1=﹣x2﹣x,
故答案为:y=﹣x2﹣x.
四、解答题(本题共7小题,共64分。解答应写出文字说明、证明过程或演算步栗)
17.已知关于x的方程x2﹣2kx﹣=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣2,求另一个根及k值.
【分析】(1)计算判别式的值,然后利用判别式的意义得到结论;
(2)设方程的另一个根为t,利用根与系数的关系得到﹣2+t=2k,﹣2t=﹣,然后先求出t,再求k的值.
【解答】(1)证明:∵Δ=4k2+2>0,
∴方程x2﹣2kx﹣=0有两个不相等的实数根;
(2)解:设方程的另一个根为t,
根据题意得﹣2+t=2k,﹣2t=﹣,
解得t=,k=﹣,
∴k=﹣,另一根为.
18.北京冬奥会将在2022年2月4日至20日举行,北京将成为奥运史上第一个举办过夏季奥运会和冬季奥运会的城市.小亮是个集邮爱好者,他收集了如图所示的5张纪念邮票(除正面内容不同外,其余均相同),现将5张邮票背面朝上,洗匀放好.
(1)小亮从中随机抽取一张邮票是“吉祥物雪容融”的概率是 ;
(2)小明发明了一种“邮票棋”比胜负的游戏,用小亮的三种邮票当作5颗棋子,其中冬奥会会徽邮票记作A棋,吉祥物冰敦敦邮票记作B棋,吉祥物雪容融邮票记作C棋.
游戏规则:将5颗棋子放入一个不透明的袋子中,然后随机从5颗棋子中摸出1颗棋子,不放回,再摸出第2颗棋子.若摸到A棋,则小明胜;若摸到两颗相同的棋子,则小亮胜;其余情况视为平局,游戏重新进行,请你用列表或画树状图的方法验证这个游戏公平吗?请说明理由.
【分析】(1)直接根据概率公式求解即可;
(2)列表得出所有等可能结果,从中找到符合条件的结果,求出两人获胜的概率,比较大小即可得出答案.
解:(1)小亮从中随机抽取一张邮票是“吉祥物雪容融”的概率是,
故答案为:.
(2)此游戏不公平,理由如下:
列表如下:
A B B C C
A (B,A) (B,A) (C,A) (C,A)
B (A,B) (B,B) (C,B) (C,B)
B (A,B) (B,B) (C,B) (C,B)
C (A,C) (B,C) (B,C) (C,C)
C (A,C) (B,C) (B,C) (C,C)
由表知,共有20种等可能结果,其中摸到A棋的有8种结果,摸到两颗相同的棋子的有4种结果,
所以小明获胜的概率为=,小亮获胜的概率为=,
∵≠,
∴此游戏不公平.
19.如图,在四边形ABCD中,∠B=∠DCB=90°,AB=6,CD=2,△ABP与△PCD全等.
(1)求AD的长;
(2)求tan∠DAC的值.
【分析】(1)利用全等三角形的性质证明△APD是等腰直角三角形,利用勾股定理求出PD,可得结论;
(2)过点D作DH∠AC于点H.利用相似三角形的性质求出CH,DH,即可解决问题.
解:(1)∵△ABP≌△PCD,
∴AB=CP=6,BP=CD=2,AP=PD,∠APB=∠CDP,
∵∠PCD=90°,
∴∠CPD+∠CDP=90°,
∴∠APB+∠CPD=90°,
∴∠APD=90°,
∴PD===2,
∴AD===4;
(2)过点D作DH∠AC于点H.
在Rt△ABC中,∠B=90°,AB=6,BC=8,
∴AC===10.
∵AB∥CD,
∴∠CAB=∠DCH,
∵∠B=∠CHD=90°,
∴△ABC∽△CHD,
∴==,
∴==,
∴CH=,DH=,
∴AH=AC﹣CH=10﹣=,
∴tan∠DAC===.
20.如图所示,直线y=x与反比例函数y=(k≠0,x>0)的图象交于点Q(4,a),点P(m,n)是反比例函数图象上一点,且n=2m.
(1)求反比例函数和直线PQ的解析式;
(2)若点M在x轴上,使得△PMQ的面积为3,求点M的坐标.
【分析】(1)利用待定系数法求得反比例函数解析,再利用反比例函数k的意义得P点的坐标,最后利用待定系数法得一次函数解析式;
(2)先求点A(6,0),再设M(a,0),根据S△PQM=S△PAM﹣S△QAM且△PMQ的面积为3,列出方程,解方程可得问题的答案.
解:(1)∵直线与反比例函数的图象交于点Q(4,a),
∴,
∵.
∴k=8,
∴反比例函数的解析式为,
∵点P(m,n)是反比例函数图象上一点,
∴mn=8,且n=2m,m>0,
∴m=2,n=4,
∴P(2,4),
设直线PQ的解析式为y=cx+b,
∴,
解得,
∴直线PQ的解析式为y=﹣x+6;
(2)∵直线PQ交x轴于点A,
∴令y=0,﹣x+6=0,得x=6,
∴A(6,0),
设M(a,0),
∴AM=|6﹣a|.
∵S△PQM=S△PAM﹣S△QAM且△PMQ的面积为3,
∴,
∴a=3或a=9,
∴点M的坐标为(3,0)或(9,0).
21.某水果店以进价为每千克18元购进草莓,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克,设销售单价为x元,每天的销售量为y千克,每天获利为w元.
(1)求y与x之间的函数表达式;
(2)求w与x之间的函数表达式,并求该草莓售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果商家规定这种草莓每天的销售量不低于40千克,求每天销售利润的最大值是多少元?
【分析】(1)根据“当销售单价每上涨1元,日销售量就减少5千克”可得减少的销售量为5(x﹣20)千克,进而再根据题意列出函数解析式即可;
(2)根据“总利润=(售价﹣进价)×销售数量”列出函数解析式,再根据求二次函数性质即可得答案;
(3)根据题意“每天的销售量不低于40千克”列出不等式求得x的取值范围,再由二次函数的性质求最大值.
解:(1)根据题意得,y=50﹣5(x﹣20)=﹣5x+150,
即y=﹣5x+150(x≥20);
(2)根据题意得,w=(x﹣18)(﹣5x+150)=﹣5x2+240x﹣2700,
即w与x之间的函数关系式为w=﹣5x2+240x﹣2700,
∵w=﹣5x2+240x﹣2700=﹣5(x﹣24)2+180,
且﹣5<0,
∴当x=24时,w有最大值,最大值为180,
答:w与x之间的函数关系式为:w=﹣5x2+240x﹣2700,该水果售价为每千克24元时,每天的销售利润最大,最大值为180元;
(3)由题意得,﹣5x+150≥40,
解得:x≤22,
∵w=﹣5(x﹣24)2+180,
∴当x≤24时,w随x的增大而增大,
∴当x=22时,w有最大值,最大值为:w=﹣5×(22﹣24)2+180=160,
答:商家每天销售利润的最大值是160元.
22.如图,A、B、C分别是⊙O上的点,∠B=60°,CD是⊙O的直径,CD=2,E是CD延长线上的一点,且AE=AC.
(1)求证:AE是⊙O的切线;
(2)求ED的长.
【分析】(1)首先连接OA,由∠B=60°,利用圆周角定理,即可求得∠AOC的度数,又由OA=OC,即可求得∠OAC与∠OCA的度数,利用三角形外角的性质,求得∠AOP的度数,又由AP=AC,利用等边对等角,求得∠P,则可求得∠PAO=90°,则可证得AP是⊙O的切线;
(2)由CD是⊙O的直径,即可得∠DAC=90°,然后利用直角三角形的性质与等腰三角形的判定定理,即可求得ED的长.
【解答】(1)证明:连接OA.
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠ACE=∠CAO=30°,
∴∠AOE=∠ACO+∠CAO=30°+30°=60°,
∵AE=AC,
∴∠E=∠ACE=30°,
∴∠OAE=90°,
∴OA⊥AE,
又∵OA是半径
∴AE是⊙O的切线;
(2)解:连接AD.
∵直径CD=2,
∴AO=OD=,
∵∠EAO=90°,∠E=30°,
∴EO=2AO=2,
∴ED=OE﹣OD=2﹣=.
23.如图,抛物线y=ax2﹣bx﹣与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C,直线AD交y轴于点E(0,1),与抛物线交于点D,点P是直线AD下方抛物线上一点(不与A,D重合).
(1)求抛物线的表达式与直线AD的表达式;
(2)过点P作PM∥y轴交直线AD于点M.当PM最大时,求出点P的坐标,PM的最大值为多少?
(3)若四边形APBM为菱形,直接写出点M的坐标.
【分析】(1)把A(﹣1,0),B(3,0)代入y=ax2﹣bx﹣,用待定系数法可得抛物线的表达式为y=x2﹣x﹣;设直线AD的表达式为y=kx+c,将A(﹣1,0),E(0,1)代入即得直线AD的表达式为y=x+1;
(2)设P(m,m2﹣m﹣),则M(m,m+1),可得PM=m+1﹣(m2﹣m﹣)=﹣(m﹣2)2+,由二次函数性质即得当PM最大时,点P的坐标是(2,﹣),PM的最大值为;
(3)根据四边形APBM为菱形,知PM过AB中点,故xM=1,从而可求得M(1,2).
解:(1)把A(﹣1,0),B(3,0)代入y=ax2﹣bx﹣得:
,解得,
∴抛物线的表达式为y=x2﹣x﹣;
设直线AD的表达式为y=kx+c,
将A(﹣1,0),E(0,1)代入得:
,解得,
∴直线AD的表达式为y=x+1;
(2)设P(m,m2﹣m﹣),则M(m,m+1),
∴PM=m+1﹣(m2﹣m﹣)=﹣m2+2m+=﹣(m﹣2)2+,
∵﹣<0,
∴m=2时,PM的值最大,最大值是;
此时m2﹣m﹣=×22﹣2﹣=﹣,
∴P(2,﹣);
答:当PM最大时,点P的坐标是(2,﹣),PM的最大值为;
(3)∵四边形APBM为菱形,
∴PM过AB中点,
∵A(﹣1,0),B(3,0),
∴xM==1,
在y=x+1中,令x=1得y=2,
∴M(1,2),
此时P(1,﹣2),AM=BM=BP=AP=2,四边形APBM为菱形,
∴点M的坐标为(1,2).
一、选择题(本题共8小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,多选、不选、错选均记0分.)
1.方程(x﹣1)x=2x的解是( )
A.x=3 B.x1=0,x2=3 C.x1=0,x2=1 D.x1=1,x2=3
2.某人沿着斜坡前进,当他前进30米时上升的高度为15米,则斜坡的坡度i等于( )
A.1:2 B.1: C.1: D.2:1
3.如图,⊙O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为( )
A.70° B.110° C.120° D.130°
4.如图,∠ABC=30°,边BA上有一点D,DB=6,以点D为圆心,以DB长为半径作弧交BC于点E,则BE的长是( )
A. B.6 C. D.12
5.若点A(x1,﹣3),B(x2,﹣1),C(x3,3)都在反比例函数y=(k>0)的图象上,则x1,x2,x3的大小关系是( )
A.x3>x1>x2 B.x1>x2>x3 C.x2>x1>x3 D.x1>x3>x2
6.在同一平面直角坐标系中,反比例函数y=(k≠0)与二次函数y=x2﹣kx﹣k的大致图象是( )
A. B.
C. D.
7.如图,将半径为2cm的圆形纸片翻折,使得、恰好都经过圆心O,折痕为AB、BC,则阴影部分的面积为( )
A.πcm2 B.πcm2 C.πcm2 D.πcm2
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①abc>0;②b2>4ac;③a﹣b+c<0;④a+c<1;正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、选择题(本题共4小题,每小题4分,共16分。在每小题给出的选项中,有多项符合题目要求,全部选对的得4分,有选错的得0分,部分选对的得2分。)
9.如图,∠ABC=∠BDA=90°,下列线段比值等于cosA的是 .
A.
B.
C.
D.
10.小明同学统计了某学校九年级部分同学每天阅读图书的时间,并绘制了统计图,如图所示,下面四个推断中正确的是 .
A.小明此次一共调查了100位同学
B.每天阅读图书时间在15~30分钟的人数最多
C.每天阅读图书时间不足15分钟的同学人数多于45~60分钟的人数
D.每天阅读图书时间超过30分钟的同学人数是调查总人数的20%
11.如图,PA、PB是⊙O的切线,切点分别为A、B,BC是⊙O的直径,PO交⊙O于E点,连接AB交PO于F,连接CE交AB于D点.下列结论正确的是 .
A.CE平分∠ACB
B.△CDA≌△EDF
C.E是△PAB的内心
D.OF=AC
12.对于实数a,b,定义运算“※”:a※b=,例如:4※2,因为4>2,所以4※2=42﹣4×2=8.若函数y=(2x)※(x+1),则下列结论正确的是 .
A.方程(2x)※(x+1)=0的解为x1=﹣1,x2=1
B.当x>1时,y随x的增大而增大
C.若关于x的方程(2x)※(x+1)=m有三个解,则0<m≤1
D.当x<1时,函数y=(2x)※(x+1)的最大值为1
三、填空题(本题共4小题,共16分,只要求填写最后结果,每小题填对得4分。)
13.如图,点A在反比例函数的图象上,直角△OAB的面积为2,则k= .
14.如图,四边形ABCD内接于⊙O,延长BC到E且∠DCE=66°,则∠BOD的度数是 .
15.如图,AB为订书机的托板,压柄BC绕着点B旋转,连接DE的一端点D固定,点E从A向B处滑动,在滑动的过程中,DE的长度保持不变.在图1中,BD=6cm,BE=15cm,∠B=60°,现将压柄BC从图1旋转到与底座AB垂直,如图2所示,则此过程中点E滑动的距离为 cm.
16.某桥梁的桥洞可视为抛物线,AB=12m,最高点C距离水面4m.以AB所在直线为x轴(向右为正向),若以A为原点建立坐标系时,该抛物线的表达式为y=﹣x2+x.已知点D为抛物线上一点,位于点C右侧且距离水面3m,若以点D为原点,以平行于AB的直线为x轴(向右为正向)建立坐标系时,该抛物线的表达式为 .
四、解答题(本题共7小题,共64分。解答应写出文字说明、证明过程或演算步栗)
17.已知关于x的方程x2﹣2kx﹣=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣2,求另一个根及k值.
18.北京冬奥会将在2022年2月4日至20日举行,北京将成为奥运史上第一个举办过夏季奥运会和冬季奥运会的城市.小亮是个集邮爱好者,他收集了如图所示的5张纪念邮票(除正面内容不同外,其余均相同),现将5张邮票背面朝上,洗匀放好.
(1)小亮从中随机抽取一张邮票是“吉祥物雪容融”的概率是 ;
(2)小明发明了一种“邮票棋”比胜负的游戏,用小亮的三种邮票当作5颗棋子,其中冬奥会会徽邮票记作A棋,吉祥物冰敦敦邮票记作B棋,吉祥物雪容融邮票记作C棋.
游戏规则:将5颗棋子放入一个不透明的袋子中,然后随机从5颗棋子中摸出1颗棋子,不放回,再摸出第2颗棋子.若摸到A棋,则小明胜;若摸到两颗相同的棋子,则小亮胜;其余情况视为平局,游戏重新进行,请你用列表或画树状图的方法验证这个游戏公平吗?请说明理由.
19.如图,在四边形ABCD中,∠B=∠DCB=90°,AB=6,CD=2,△ABP与△PCD全等.
(1)求AD的长;
(2)求tan∠DAC的值.
20.如图所示,直线y=x与反比例函数y=(k≠0,x>0)的图象交于点Q(4,a),点P(m,n)是反比例函数图象上一点,且n=2m.
(1)求反比例函数和直线PQ的解析式;
(2)若点M在x轴上,使得△PMQ的面积为3,求点M的坐标.
21.某水果店以进价为每千克18元购进草莓,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克,设销售单价为x元,每天的销售量为y千克,每天获利为w元.
(1)求y与x之间的函数表达式;
(2)求w与x之间的函数表达式,并求该草莓售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果商家规定这种草莓每天的销售量不低于40千克,求每天销售利润的最大值是多少元?
22.如图,A、B、C分别是⊙O上的点,∠B=60°,CD是⊙O的直径,CD=2,E是CD延长线上的一点,且AE=AC.
(1)求证:AE是⊙O的切线;
(2)求ED的长.
23.如图,抛物线y=ax2﹣bx﹣与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C,直线AD交y轴于点E(0,1),与抛物线交于点D,点P是直线AD下方抛物线上一点(不与A,D重合).
(1)求抛物线的表达式与直线AD的表达式;
(2)过点P作PM∥y轴交直线AD于点M.当PM最大时,求出点P的坐标,PM的最大值为多少?
(3)若四边形APBM为菱形,直接写出点M的坐标.
参考答案
一、选择题(本题共8小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,多选、不选、错选均记0分.)
1.方程(x﹣1)x=2x的解是( )
A.x=3 B.x1=0,x2=3 C.x1=0,x2=1 D.x1=1,x2=3
【分析】整理后把方程的左边分解因式,即可得出两个一元一次方程,再求出方程的解即可.
解:(x﹣1)x=2x,
整理得:x2﹣3x=0,
x(x﹣3)=0,
x=0或x﹣3=0,
解得:x1=0,x2=3,
故选:B.
2.某人沿着斜坡前进,当他前进30米时上升的高度为15米,则斜坡的坡度i等于( )
A.1:2 B.1: C.1: D.2:1
【分析】由某人在斜坡上走了30米,上升的高度为15米,则可先求出某人走的水平距离,再求出这个斜坡的坡度.
解:由题意得:某人在斜坡上走了30米,上升的高度为15米,
则某人走的水平距离s==15(米),
∴坡度i=15:15=1:.
故选:C.
3.如图,⊙O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为( )
A.70° B.110° C.120° D.130°
【分析】先根据三角形的内角和定理求得∠B,再由切线的性质得∠BDO=∠BEO=90°,从而得出∠DOE.
解:∵∠BAC=50°,∠ACB=60°,
∴∠B=180°﹣50°﹣60°=70°,
∵E,D是切点,
∴∠BDO=∠BEO=90°,
∴∠DOE=180°﹣∠B,
∴∠DOE=∠A+∠C=50°+60°=110°.
故选:B.
4.如图,∠ABC=30°,边BA上有一点D,DB=6,以点D为圆心,以DB长为半径作弧交BC于点E,则BE的长是( )
A. B.6 C. D.12
【分析】过点D作DF⊥BC于F,则BE=2BF,∠BFD=90°,再利用含30度角的直角三角形的性质求出DF,进而求出BF,即可求出答案.
解:过点D作DF⊥BC于F,则BE=2BF,∠BFD=90°,
在Rt△BFD中,∠ABC=30°,BD=6,
∴DF=BD=3,
∴BF=DF=3,
∴BE=2BF=6,
故选:C.
5.若点A(x1,﹣3),B(x2,﹣1),C(x3,3)都在反比例函数y=(k>0)的图象上,则x1,x2,x3的大小关系是( )
A.x3>x1>x2 B.x1>x2>x3 C.x2>x1>x3 D.x1>x3>x2
【分析】先根据反比例函数的解析式判断出函数图象所在的象限,再根据根据反比例函数的性质,可以判断出x1,x2,x3的大小关系,本题得以解决.
解:∵反比例函数y=中k>0,
∴函数图象的两个分支分别位于一、三象限,且在每一象限内,y随x的增大而减小.
∵点A(x1,﹣3),B(x2,﹣1),C(x3,3)都在反比例函数y=(k>0)的图象上,﹣3<﹣1<0<3,
∴x2<x1<x3,
故选:A.
6.在同一平面直角坐标系中,反比例函数y=(k≠0)与二次函数y=x2﹣kx﹣k的大致图象是( )
A. B.
C. D.
【分析】根据k的取值范围分当k>0时和当k<0时两种情况进行讨论,根据反比例函数图象与性质,二次函数图象和性质进行判断即可.
解:当k>0时,反比例函数y=(k≠0)的图象经过第一、三象限,二次函数y=x2﹣kx﹣k图象的对称轴x=在y轴右侧,并与y'轴交于负半轴,则B选项不符合题意,D选项符合题意;
当k<0时,反比例函数y=(k≠0)的图象经过第二、四象限,二次函数y=x2+kx﹣k图象的对称轴x=在y轴左侧,并与y'轴交于正半轴,则A、C选项都不符合题意;
故选:D.
7.如图,将半径为2cm的圆形纸片翻折,使得、恰好都经过圆心O,折痕为AB、BC,则阴影部分的面积为( )
A.πcm2 B.πcm2 C.πcm2 D.πcm2
【分析】作OD⊥AB于点D,连接AO,BO,CO,求出∠OAD=30°,得到∠AOB=2∠AOD=120°,进而求得∠AOC=120°,再利用阴影部分的面积=S扇形AOC得出阴影部分的面积是⊙O面积的,即可得出结果.
解:作OD⊥AB于点D,连接AO,BO,CO,如图所示:
∵OD=AO
∴∠OAD=30°,
∴∠AOB=2∠AOD=120°,
同理∠BOC=120°,
∴∠AOC=120°,
∴阴影部分的面积=S扇形BOC=×⊙O面积=×π×22=π(cm2);
故选:C.
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①abc>0;②b2>4ac;③a﹣b+c<0;④a+c<1;正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】①由开口向上得到a>0,由对称轴在y轴左侧得到b>0,由函数图象与y轴的交点在y轴负半轴上得到c<0,然后得到abc<0;
②由函数图象与x轴的交点个数得到b2﹣4ac>0;
③由图象可知,当x=﹣1时,y=a﹣b+c<0;
④由图象可知,当x=1时,y=2,得到a+b+c=2,然后得到b与a、c之间的关系,再代入a﹣b+c<0得到结果.
解:①∵开口向上,对称轴在y轴左侧,函数图象与y轴的交点在y轴负半轴上,
∴a>0,b>0,c<0,
∴abc<0,故①错误,不符合题意;
②由图可知,函数图象与x轴由2个交点,
∴b2﹣4ac>0,
∴b2>4ac,故②正确,符合题意;
③由图象可知,当x=﹣1时,y<0,
∴a﹣b+c<0,故③正确,符合题意;
④由图象可知,当x=1时,y=2,
∴a+b+c=2,
∴b=2﹣a﹣c,
∵a﹣b+c<0,
∴a﹣(2﹣a﹣c)+c<0,
∴a+c<1,故④正确,符合题意,
∴正确的个数有3个,
故选:C.
二、选择题(本题共4小题,每小题4分,共16分。在每小题给出的选项中,有多项符合题目要求,全部选对的得4分,有选错的得0分,部分选对的得2分。)
9.如图,∠ABC=∠BDA=90°,下列线段比值等于cosA的是 C、D .
A.
B.
C.
D.
【分析】根据余弦等于邻边比斜边,可得答案.
解:A、在Rt△ABD中,cosA=,故本选项错误,不符合题意;
B、在Rt△ABC中,cosA=,故本选项错误,不符合题意;
C、在Rt△BCD中,cosA=cos∠DBC=,故本选项正确,符合题意;
D、在Rt△ABC中,cosA=,故本选项正确,符合题意;
故选:C、D.
10.小明同学统计了某学校九年级部分同学每天阅读图书的时间,并绘制了统计图,如图所示,下面四个推断中正确的是 A、B .
A.小明此次一共调查了100位同学
B.每天阅读图书时间在15~30分钟的人数最多
C.每天阅读图书时间不足15分钟的同学人数多于45~60分钟的人数
D.每天阅读图书时间超过30分钟的同学人数是调查总人数的20%
【分析】根据频数分布直方图的意义,逐项进行判断即可.
解:10+60+20+10=100(人),因此选项A是正确的;
每天阅读图书时间在15~30分钟的人数为60人,是几个时间段人数最多的,因此选项B是正确的;
每天阅读图书时间不足15分钟的同学人数与阅读时间在45~60分钟的人数相等,都是10人,因此选项C不正确;
每天阅读图书时间超过30分钟的同学人数是调查总人数的=30%,因此选项D不正确;
故答案为:A、B.
11.如图,PA、PB是⊙O的切线,切点分别为A、B,BC是⊙O的直径,PO交⊙O于E点,连接AB交PO于F,连接CE交AB于D点.下列结论正确的是 A,C,D .
A.CE平分∠ACB
B.△CDA≌△EDF
C.E是△PAB的内心
D.OF=AC
【分析】连接OA,BE,根据PA、PB是⊙O的切线,可得PA=PB,OA=OB,可得OP是AB的垂直平分线,根据垂径定理,进而可以判断A;根据OB=OC,AF=BF,可得OF是三角形BAC的中位线,进而即可判断D;证明∠PBE=∠EBA,∠APE=∠BPE,即可判断C;根据AC∥OE,可得△CDA∽△EDF,进而可以判断B.
解:如图,连接OA,BE,
∵PA、PB是⊙O的切线,
∴PA=PB,
∵OA=OB,
∴OP是AB的垂直平分线,
∴OP⊥AB,
∴=,
∴∠ACE=∠BCE,
∴CE平分∠ACB;故A正确;
∵BC是⊙O的直径,
∴∠BAC=90°,
∵∠BFO=90°,
∴OF∥AC,
∵OB=OC,AF=BF,
∴OF=AC;故D正确;
∵PB是⊙O的切线,
∴∠PBE+∠EBC=90°,
∵BC是⊙O的直径,
∴∠EBC+∠ECB=90°,
∴∠PBE=∠ECB,
∵∠ECB=∠EBA,
∴∠PBE=∠EBA,
∵∠APE=∠BPE,
∴E是△PAB的内心;故C正确;
∵AC∥OE,
∴△CDA∽△EDF.故B错误;
∴结论正确的是A,C,D.
故答案为:A,C,D.
12.对于实数a,b,定义运算“※”:a※b=,例如:4※2,因为4>2,所以4※2=42﹣4×2=8.若函数y=(2x)※(x+1),则下列结论正确的是 ABD .
A.方程(2x)※(x+1)=0的解为x1=﹣1,x2=1
B.当x>1时,y随x的增大而增大
C.若关于x的方程(2x)※(x+1)=m有三个解,则0<m≤1
D.当x<1时,函数y=(2x)※(x+1)的最大值为1
【分析】根据题干定义求出y=(2x)※(x+1)的解析式,根据2x≥x+1及2x<x+1可得x≥1时y=2x2﹣2x,x<1时,y=﹣x2+1,进而求解.
解:根据题意得:当2x≥x+1,即x≥1时,y=(2x)2﹣2x(x+1)=2x2﹣2x,
当2x<x+1,即x<1时,y=(x+1)2﹣2x(x+1)=﹣x2+1,
∴当x≥1时,2x2﹣2x=0,
解得x=0(舍去)或x=1,
当x<1时,﹣x2+1=0,
解得x=1(舍去)或x=﹣1,
∴(2x)※(x+1)=0的解是x1=﹣1,x2=1;
故A正确,
B、当x>1时,y=2x2﹣2x,
抛物线开口向上,对称轴是直线x=,
∴x>1时,y随x的增大而增大,
∴B选项正确.
当x≥1时,y=2x2﹣2x=2(x﹣)2﹣,
∴x=1时,y取最小值为y=0,
当x<1时,y=﹣x2+1=0,
当x=0时,y取最大值为y=1,
如图,
当0<m<1时,方程(2x)※(x+1)=m有三个解,
∴选项C错误,选项D正确.
故答案为:ABD.
三、填空题(本题共4小题,共16分,只要求填写最后结果,每小题填对得4分。)
13.如图,点A在反比例函数的图象上,直角△OAB的面积为2,则k= ﹣4 .
【分析】设A点坐标为(a,b),由于点A在反比例函数图象上,则k=ab,然后利用三角形面积公式得到×(﹣a)×b=2,则ab=﹣4,即可得到k=﹣4.
解:设A点坐标为(a,b),则k=ab,
∵S△OAB=AB OB,
∴×(﹣a)×b=2,
∴ab=﹣4,
∴k=﹣4.
故答案为﹣4.
14.如图,四边形ABCD内接于⊙O,延长BC到E且∠DCE=66°,则∠BOD的度数是 132° .
【分析】根据圆内接四边形的性质可直接得出结论.
解:∵四边形ABCD是圆内接四边形,∠DCE=66°,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠A=∠DCE=66°,
∴∠BOD=2∠A=132°.
故答案为:132°.
15.如图,AB为订书机的托板,压柄BC绕着点B旋转,连接DE的一端点D固定,点E从A向B处滑动,在滑动的过程中,DE的长度保持不变.在图1中,BD=6cm,BE=15cm,∠B=60°,现将压柄BC从图1旋转到与底座AB垂直,如图2所示,则此过程中点E滑动的距离为 (15﹣3) cm.
【分析】如图1,由直角三角形的性质和勾股定理可求DE的长,如图2,由勾股定理可求BE的长,即可求解.
解:如图1,过点D作DH⊥AB于H,
∵∠ABC=60°,
∴∠BDH=30°,
∴DH=BD=3(cm),DH=BH=3(cm),
∴EH=15﹣3=12(cm),
∴DE===3(cm),
如图2,∵∠DBE=90°,
∴BE===3(cm),
∴点E滑动的距离=(15﹣3)cm,
故答案为:(15﹣3).
16.某桥梁的桥洞可视为抛物线,AB=12m,最高点C距离水面4m.以AB所在直线为x轴(向右为正向),若以A为原点建立坐标系时,该抛物线的表达式为y=﹣x2+x.已知点D为抛物线上一点,位于点C右侧且距离水面3m,若以点D为原点,以平行于AB的直线为x轴(向右为正向)建立坐标系时,该抛物线的表达式为 y=﹣x2﹣x .
【分析】在y=﹣x2+x中,令y=3可得xD﹣xA=9,以点D为原点,以平行于AB的直线为x轴(向右为正向)建立坐标系,根据题意知此时顶点D(﹣3,1),A(﹣9,﹣3),设抛物线的表达式为y=a(x+3)2+1,将A(﹣9,﹣3)代入即得抛物线的表达式为y=﹣(x+3)2+1=﹣x2﹣x.
解:在y=﹣x2+x中,令y=3得﹣x2+x=3,
解得x=3或x=9,
∵点D为抛物线上一点,位于点C右侧且距离水面3m,
∴xD﹣xA=9,
以点D为原点,以平行于AB的直线为x轴(向右为正向)建立坐标系,如图:
根据题意知此时顶点D(﹣3,1),A(﹣9,﹣3),
设抛物线的表达式为y=a(x+3)2+1,
将A(﹣9,﹣3)代入得:36a+1=﹣3,
解得a=﹣,
∴抛物线的表达式为y=﹣(x+3)2+1=﹣x2﹣x,
故答案为:y=﹣x2﹣x.
四、解答题(本题共7小题,共64分。解答应写出文字说明、证明过程或演算步栗)
17.已知关于x的方程x2﹣2kx﹣=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣2,求另一个根及k值.
【分析】(1)计算判别式的值,然后利用判别式的意义得到结论;
(2)设方程的另一个根为t,利用根与系数的关系得到﹣2+t=2k,﹣2t=﹣,然后先求出t,再求k的值.
【解答】(1)证明:∵Δ=4k2+2>0,
∴方程x2﹣2kx﹣=0有两个不相等的实数根;
(2)解:设方程的另一个根为t,
根据题意得﹣2+t=2k,﹣2t=﹣,
解得t=,k=﹣,
∴k=﹣,另一根为.
18.北京冬奥会将在2022年2月4日至20日举行,北京将成为奥运史上第一个举办过夏季奥运会和冬季奥运会的城市.小亮是个集邮爱好者,他收集了如图所示的5张纪念邮票(除正面内容不同外,其余均相同),现将5张邮票背面朝上,洗匀放好.
(1)小亮从中随机抽取一张邮票是“吉祥物雪容融”的概率是 ;
(2)小明发明了一种“邮票棋”比胜负的游戏,用小亮的三种邮票当作5颗棋子,其中冬奥会会徽邮票记作A棋,吉祥物冰敦敦邮票记作B棋,吉祥物雪容融邮票记作C棋.
游戏规则:将5颗棋子放入一个不透明的袋子中,然后随机从5颗棋子中摸出1颗棋子,不放回,再摸出第2颗棋子.若摸到A棋,则小明胜;若摸到两颗相同的棋子,则小亮胜;其余情况视为平局,游戏重新进行,请你用列表或画树状图的方法验证这个游戏公平吗?请说明理由.
【分析】(1)直接根据概率公式求解即可;
(2)列表得出所有等可能结果,从中找到符合条件的结果,求出两人获胜的概率,比较大小即可得出答案.
解:(1)小亮从中随机抽取一张邮票是“吉祥物雪容融”的概率是,
故答案为:.
(2)此游戏不公平,理由如下:
列表如下:
A B B C C
A (B,A) (B,A) (C,A) (C,A)
B (A,B) (B,B) (C,B) (C,B)
B (A,B) (B,B) (C,B) (C,B)
C (A,C) (B,C) (B,C) (C,C)
C (A,C) (B,C) (B,C) (C,C)
由表知,共有20种等可能结果,其中摸到A棋的有8种结果,摸到两颗相同的棋子的有4种结果,
所以小明获胜的概率为=,小亮获胜的概率为=,
∵≠,
∴此游戏不公平.
19.如图,在四边形ABCD中,∠B=∠DCB=90°,AB=6,CD=2,△ABP与△PCD全等.
(1)求AD的长;
(2)求tan∠DAC的值.
【分析】(1)利用全等三角形的性质证明△APD是等腰直角三角形,利用勾股定理求出PD,可得结论;
(2)过点D作DH∠AC于点H.利用相似三角形的性质求出CH,DH,即可解决问题.
解:(1)∵△ABP≌△PCD,
∴AB=CP=6,BP=CD=2,AP=PD,∠APB=∠CDP,
∵∠PCD=90°,
∴∠CPD+∠CDP=90°,
∴∠APB+∠CPD=90°,
∴∠APD=90°,
∴PD===2,
∴AD===4;
(2)过点D作DH∠AC于点H.
在Rt△ABC中,∠B=90°,AB=6,BC=8,
∴AC===10.
∵AB∥CD,
∴∠CAB=∠DCH,
∵∠B=∠CHD=90°,
∴△ABC∽△CHD,
∴==,
∴==,
∴CH=,DH=,
∴AH=AC﹣CH=10﹣=,
∴tan∠DAC===.
20.如图所示,直线y=x与反比例函数y=(k≠0,x>0)的图象交于点Q(4,a),点P(m,n)是反比例函数图象上一点,且n=2m.
(1)求反比例函数和直线PQ的解析式;
(2)若点M在x轴上,使得△PMQ的面积为3,求点M的坐标.
【分析】(1)利用待定系数法求得反比例函数解析,再利用反比例函数k的意义得P点的坐标,最后利用待定系数法得一次函数解析式;
(2)先求点A(6,0),再设M(a,0),根据S△PQM=S△PAM﹣S△QAM且△PMQ的面积为3,列出方程,解方程可得问题的答案.
解:(1)∵直线与反比例函数的图象交于点Q(4,a),
∴,
∵.
∴k=8,
∴反比例函数的解析式为,
∵点P(m,n)是反比例函数图象上一点,
∴mn=8,且n=2m,m>0,
∴m=2,n=4,
∴P(2,4),
设直线PQ的解析式为y=cx+b,
∴,
解得,
∴直线PQ的解析式为y=﹣x+6;
(2)∵直线PQ交x轴于点A,
∴令y=0,﹣x+6=0,得x=6,
∴A(6,0),
设M(a,0),
∴AM=|6﹣a|.
∵S△PQM=S△PAM﹣S△QAM且△PMQ的面积为3,
∴,
∴a=3或a=9,
∴点M的坐标为(3,0)或(9,0).
21.某水果店以进价为每千克18元购进草莓,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克,设销售单价为x元,每天的销售量为y千克,每天获利为w元.
(1)求y与x之间的函数表达式;
(2)求w与x之间的函数表达式,并求该草莓售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果商家规定这种草莓每天的销售量不低于40千克,求每天销售利润的最大值是多少元?
【分析】(1)根据“当销售单价每上涨1元,日销售量就减少5千克”可得减少的销售量为5(x﹣20)千克,进而再根据题意列出函数解析式即可;
(2)根据“总利润=(售价﹣进价)×销售数量”列出函数解析式,再根据求二次函数性质即可得答案;
(3)根据题意“每天的销售量不低于40千克”列出不等式求得x的取值范围,再由二次函数的性质求最大值.
解:(1)根据题意得,y=50﹣5(x﹣20)=﹣5x+150,
即y=﹣5x+150(x≥20);
(2)根据题意得,w=(x﹣18)(﹣5x+150)=﹣5x2+240x﹣2700,
即w与x之间的函数关系式为w=﹣5x2+240x﹣2700,
∵w=﹣5x2+240x﹣2700=﹣5(x﹣24)2+180,
且﹣5<0,
∴当x=24时,w有最大值,最大值为180,
答:w与x之间的函数关系式为:w=﹣5x2+240x﹣2700,该水果售价为每千克24元时,每天的销售利润最大,最大值为180元;
(3)由题意得,﹣5x+150≥40,
解得:x≤22,
∵w=﹣5(x﹣24)2+180,
∴当x≤24时,w随x的增大而增大,
∴当x=22时,w有最大值,最大值为:w=﹣5×(22﹣24)2+180=160,
答:商家每天销售利润的最大值是160元.
22.如图,A、B、C分别是⊙O上的点,∠B=60°,CD是⊙O的直径,CD=2,E是CD延长线上的一点,且AE=AC.
(1)求证:AE是⊙O的切线;
(2)求ED的长.
【分析】(1)首先连接OA,由∠B=60°,利用圆周角定理,即可求得∠AOC的度数,又由OA=OC,即可求得∠OAC与∠OCA的度数,利用三角形外角的性质,求得∠AOP的度数,又由AP=AC,利用等边对等角,求得∠P,则可求得∠PAO=90°,则可证得AP是⊙O的切线;
(2)由CD是⊙O的直径,即可得∠DAC=90°,然后利用直角三角形的性质与等腰三角形的判定定理,即可求得ED的长.
【解答】(1)证明:连接OA.
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠ACE=∠CAO=30°,
∴∠AOE=∠ACO+∠CAO=30°+30°=60°,
∵AE=AC,
∴∠E=∠ACE=30°,
∴∠OAE=90°,
∴OA⊥AE,
又∵OA是半径
∴AE是⊙O的切线;
(2)解:连接AD.
∵直径CD=2,
∴AO=OD=,
∵∠EAO=90°,∠E=30°,
∴EO=2AO=2,
∴ED=OE﹣OD=2﹣=.
23.如图,抛物线y=ax2﹣bx﹣与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C,直线AD交y轴于点E(0,1),与抛物线交于点D,点P是直线AD下方抛物线上一点(不与A,D重合).
(1)求抛物线的表达式与直线AD的表达式;
(2)过点P作PM∥y轴交直线AD于点M.当PM最大时,求出点P的坐标,PM的最大值为多少?
(3)若四边形APBM为菱形,直接写出点M的坐标.
【分析】(1)把A(﹣1,0),B(3,0)代入y=ax2﹣bx﹣,用待定系数法可得抛物线的表达式为y=x2﹣x﹣;设直线AD的表达式为y=kx+c,将A(﹣1,0),E(0,1)代入即得直线AD的表达式为y=x+1;
(2)设P(m,m2﹣m﹣),则M(m,m+1),可得PM=m+1﹣(m2﹣m﹣)=﹣(m﹣2)2+,由二次函数性质即得当PM最大时,点P的坐标是(2,﹣),PM的最大值为;
(3)根据四边形APBM为菱形,知PM过AB中点,故xM=1,从而可求得M(1,2).
解:(1)把A(﹣1,0),B(3,0)代入y=ax2﹣bx﹣得:
,解得,
∴抛物线的表达式为y=x2﹣x﹣;
设直线AD的表达式为y=kx+c,
将A(﹣1,0),E(0,1)代入得:
,解得,
∴直线AD的表达式为y=x+1;
(2)设P(m,m2﹣m﹣),则M(m,m+1),
∴PM=m+1﹣(m2﹣m﹣)=﹣m2+2m+=﹣(m﹣2)2+,
∵﹣<0,
∴m=2时,PM的值最大,最大值是;
此时m2﹣m﹣=×22﹣2﹣=﹣,
∴P(2,﹣);
答:当PM最大时,点P的坐标是(2,﹣),PM的最大值为;
(3)∵四边形APBM为菱形,
∴PM过AB中点,
∵A(﹣1,0),B(3,0),
∴xM==1,
在y=x+1中,令x=1得y=2,
∴M(1,2),
此时P(1,﹣2),AM=BM=BP=AP=2,四边形APBM为菱形,
∴点M的坐标为(1,2).
同课章节目录
